1 is not a prime nuber.explain your statement
Answers
Answer:
1 can only be divided by one number, 1 itself, so with this definition 1 is not a prime number. It is important to remember that mathematical definitions develop and evolve. Throughout history, many mathematicians considered 1 to be a prime number although that is not now a commonly held view.
Step-by-step explanation:
Related Questions
Explain why the function is differentiable at the given point.
f(x, y) = 5 + x ln(xy − 9), (5, 2)
Answers
Step-by-step explanation:
Given the function
f(x, y) = 5 + x ln(xy − 9) at the point (5, 2)
For the function to be differentiable at the given point, the differential of the function with respect to x and y must be continuous at the point.
Fx is the differential of the function with respect to x.
Using product rule to get f(x):
fx = 0 + x(1/(xy-9)y) + ln(xy-9)
fx = xy(1/(xy-9)) + ln(xy-9)
Substitute point (5, 2) into fx
fx = 5(2)(1/5(2)-9) + ln(5(2)-9)
fx = 10(1/(10-9)) + ln(10-9)
fx = 10(1/1) + ln1
fx = 10 + 0
fx = 10
For fy:
fy = 0 + x²(1/(xy-9))+ 0
fy = x²(1/(xy-9))
Substitute point (5, 2) into fy
fy = 5²(1/(5(2)-9))
fy = 25(1/10-9)
fy = 25(1/1)
fy = 25
Next is to calculate f(5,2)
f(5,2) = 5 + 5 ln(2(5) − 9)
f(5,2) = 5 + 5 ln(10− 9)
f(5,2) = 5 + 5 ln1
f(5,2) = 5 + 5(0)
f(5,2) = 5
Since fx ≠ fy, hence the function is not differentiable at the given point
what is 5/8 with a denominator of 24?
Answers
Answer:
Step-by-step explanation:
you multiply 8*3 to get 24 so you do the same to 5. so 5*3 = 15 so 15/24
Which of the following shows a 90° counterclockwise rotation of the blue figure
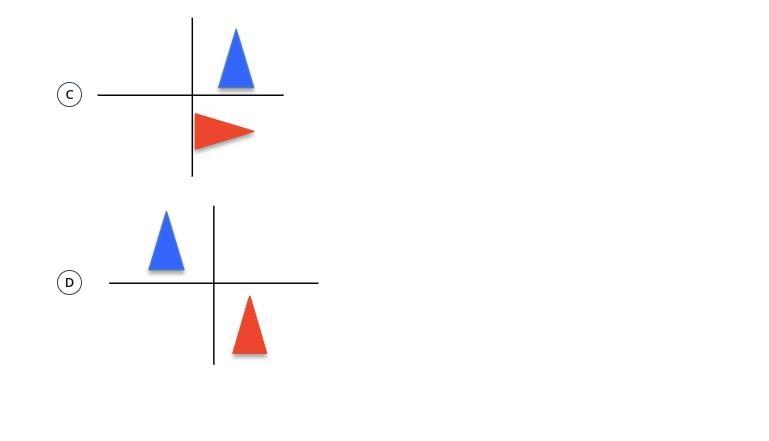

Answers
Elaina Kicks A Soccer Ball With An Initial Velocity Of

Answers
By using the motion equations, we conclude that she will make the goal.
Will she make the goal?
First, we know that the goal is 20ft away, and the position in x is given by:
\(x = 28*cos(58)*t\)
Let's find the time in which the ball will travel these 20 ft.
\(20 = 28*cos(58)*t\)
\((20)/(28*cos(58)) = t = 1.35\)
So the horizontal distance is covered in 1.35 seconds, now let's see which is the height of the ball at that time.
The height equation is:
\(y = -16*t^2 +28*sin(58)*t\)
Evaluating in t = 1.35 we get:
\(y = -16*(1.35)^2 +28*sin(58)*1.35\\\\y = 2.9\)
And the goal is 5ft tall, so we can conclude that she will make the goal.
If you want to learn more about motion equations:
https://brainly.com/question/19365526
#SPJ1
The following are ages of 17 of the signers of the Declaration of Independence.
49, 34, 42, 43, 39, 36, 50, 44, 45, 33, 34, 27, 33, 69, 46, 50, 41
Send data to calculator
Find 25th and 80th percentiles for these ages.
(If necessary, consult a list of formulas.)
(a) The 25th percentile:
The 80th
percentile:
Answers
Answer:
Step-by-step explanation:
The problem specifies that you may use a calculator. The formula, as reference, is:
You can use a regular calculator or an online spreadsheet to solve. In sheets, arrange your data and use the =PERCENTILE( ) function. In the parentheses, write the range of your data and the requested percentile as a decimal. So if I type the data (the ages of the signers for this example) in cells A:4 through A:23, I'd write =percentile(A7:A23,0.25).
So the answers:
25th percentile is 34.
80th percentile is 48.4.
A jar contains 100ml of a mixture of oil and water in the ratio 1:4. Enough oil is added to make the ratio of oil to water 1:2. How much water must be added to make the ratio oil to water 1:3?
Answers
Answer:
40 ml of water must be added.Step-by-step explanation:
Initial volume of mixture is 100 ml with oil to water ratio of 1 : 4.
First, let's find the volume of each component.
If the oil is x then water is 4x according to ratio and their sum is 100 ml:
x + 4x = 1005x = 100x = 20So, we have 20 ml of oil and 80 ml of water.
Now, let's added volume of oil be y. Then we have the ratio:
(20 + y)/80 = 1/220 + y = 40y = 20So, we have 40 ml of oil and 80 ml of water.
Lastly, let's added water be z. Then we have the ratio:
40/(80 + z) = 1/380 + z = 120z = 40We must add 40 ml of water.
The red figure is similar to the blue figure. Which best describes a sequence of transformations in which the blue figure is the image of the red figure?
A.Rotate 90° clockwise about the origin and then dilate with respect to the origin using a scale factor of 12.
B.Rotate 90° counterclockwise about the origin and then dilate with respect to the origin using a scale factor of 12.
C.Rotate 90° counterclockwise about the origin and then dilate with respect to the origin using a scale factor of 2.
D.Rotate 180° counterclockwise about the origin and then dilate with respect to the origin using a scale factor of 3.

Answers
The statement that best describes a sequence of transformations in which the blue figure is the image of the red figure is given as follows:
A. Rotate 90° clockwise about the origin and then dilate with respect to the origin using a scale factor of 1/2.
What are the transformations?The horizontal side lengths on the blue figure are given as follows:
8 - 4 = 6 - 2 = 4.
The vertical side lengths on the transformed red figure is of:
4 - 2 = 3 - 1 = 2.
Hence the scale factor of the dilation is given as follows:
2/4 = 1/2.
Which means that options C and D are not correct.
The rules for each rotation are given as follows:
90º degrees clockwise: (x,y) -> (y,-x).90º degrees counter-clockwise: (x,y) -> (-y,x).On the second quadrant, of the blue figure, we have that:
x is negative.y is positive.On the first quadrant, of the red figure, we have that:
x is positive.y is positive.Hence the rotation was clockwise, and option A is correct.
More can be learned about transformations at https://brainly.com/question/28792248
#SPJ1
in the figure below ABC- XZY
find cosZ, sin Z, tan Z
round your answer to the nearest hundredth

Answers
The magnitude of angle Z include the following:
cosZ = 0.471
sinZ = 0.88
tanZ = 1.875
How to calculate the magnitude of angle Z?In order to determine the magnitude of angle Z, we would apply the basic trigonometric ratio because the given side lengths represent the adjacent side, opposite side, and hypotenuse of a right-angled triangle.
cos(θ) = Adj/Hyp
Where:
Adj represents the adjacent side of a right-angled triangle.Hyp represents the hypotenuse of a right-angled triangle.θ represents the angle.For cosZ, we would apply the cosine trigonometric ratio as follows;
cosZ = 13.6/28.9
cosZ = 0.4706
Z = cos⁻¹(0.4706)
Z = 61.93°.
For sinZ, we would apply the sine trigonometric ratio as follows;
sinZ = 25.5/28.9
sinZ = 0.8824
Z = sin⁻¹(0.8824)
Z = 118.07.
For tanZ, we would apply the sine trigonometric ratio as follows;
tanZ = 25.5/13.6
tanZ = 1.875
Z = tan⁻¹(1.875)
Z = 61.93.
The following selected information was extracted from the records of B Solomon.
1. B Solomon, the owner of Solomon Traders, bought a new Machine for R250 000 on 1 July 2013.
2. On 1 October 2014, he purchased a second Machine for R350 000 cash.
3. On 30 June 2015, the Machine bought during 2013 was sold for R120 000 cash.
4. It is the business’ policy to depreciate Machines at 20% per annum on cost.
REQUIRED:
Prepare the following ledger accounts reflecting all applicable entries, in the books of Solomon Traders, properly balanced/closed off, for the years ended 31 March 2016:
1.1. Accumulated depreciation.
1.2. A Machines realisation.
NB: Show all calculations as marks will be awarded for calculations.
Answers
1.1. Accumulated depreciation:
The accumulated depreciation for the machine bought on 1 July 2013 would be R150,000 as of 31 March 2016.
1.2. Machine realization:
The machine bought in 2013 was sold for R120,000 on 30 June 2015, resulting in a profit/loss on the sale of R10,000.
1.1. Accumulated Depreciation:
To calculate the accumulated depreciation, we need to determine the annual depreciation expense for each machine and then accumulate it over the years.
Machine bought on 1 July 2013:
Cost: R250,000
Depreciation rate: 20% per annum on cost
Depreciation expense for the year ended 31 March 2014: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2015: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2016: 20% of R250,000 = R50,000
Accumulated depreciation for the machine bought on 1 July 2013:
As of 31 March 2014: R50,000
As of 31 March 2015: R100,000
As of 31 March 2016: R150,000
1.2. Machine Realisation:
To record the sale of the machine bought in 2013, we need to adjust the machine's value and the accumulated depreciation.
Machine's original cost: R250,000
Accumulated depreciation as of 30 June 2015: R100,000
Net book value as of 30 June 2015:
R250,000 - R100,000 = R150,000.
On 30 June 2015, the machine was sold for R120,000.
Realisation amount: R120,000
To record the sale:
Debit Cash: R120,000
Debit Accumulated Depreciation: R100,000
Credit Machine: R250,000
Credit Machine Realisation: R120,000
Credit Profit/Loss on Sale of Machine: R10,000 (difference between net book value and realisation amount).
These entries will reflect the appropriate balances in the ledger accounts and properly close off the accounts for the years ended 31 March 2016.
For similar question on depreciation.
https://brainly.com/question/15998639
#SPJ8
At a local university, 40% of students are male and 60% are female. In the male group, 50% major in art, 40% major in science, and the rest major in other. In the female group, 70% major in art, 10% major in science, and the rest major in other.
A.) if a student who majors in science is randomly selected, what is the probability that this student is a female?
B.) if a student is randomly selected, what is the probability that this student is a male or majors in art?
Answers
According to the given question we can conclude that the probability that a student who majors in science is a female is approximately 0.375 and the probability that a student is male or majors in art is 0.78.
Explain probability?Probability is the research of probabilities, which also are based on the ratio of favourable events to likely circumstances. One of the areas of probability theory is the estimation of the chance of experiments occurring. With a probability, we can calculate any number of things, from the probability of obtaining a head or a tail when flipping a coin towards the likelihood of generating a research error, for example.
A.) To find the probability that a student who majors in science is a female, we need to use Bayes' theorem. Let F be the event that a randomly selected student is female, and S be the event that the student majors in science. Then we have:
P(F|S) = P(S|F) * P(F) / P(S)
We know that P(F) = 0.6 (since 60% of students are female), and P(S|F) = 0.1 (since 10% of female students major in science). To find P(S), we need to use the law of total probability:
P(S) = P(S|F) * P(F) + P(S|M) * P(M)
We know that P(S|M) = 0.4 (since 40% of male students major in science), and P(M) = 0.4 (since 40% of students are male). Therefore:
P(S) = 0.1 * 0.6 + 0.4 * 0.4 = 0.16
Now we can calculate P(F|S):
P(F|S) = 0.1 * 0.6 / 0.16 ≈ 0.375
Therefore, the probability that a student who majors in science is a female is approximately 0.375.
B.) To find the probability that a student is male or majors in art, we need to use the law of total probability again:
P(Male or Art) = P(Male) + P(Art) - P(Male and Art)
We know that P(Male) = 0.4 (since 40% of students are male), and P(Art|Male) = 0.5 (since 50% of male students major in art). We also know that P(Female) = 0.6 (since 60% of students are female), and P(Art|Female) = 0.7 (since 70% of female students major in art). Therefore:
P(Art) = P(Art|Male) * P(Male) + P(Art|Female) * P(Female)
= 0.5*0.4+0.7*0.6
= 0.58
To find P(Male and Art), we can multiply the probabilities of being male and majoring in art:
P(Male and Art) = P(Male) * P(Art|Male)
= 0.4 * 0.5
= 0.2
Now we can calculate P(Male or Art):
P(Male or Art) = 0.4 + 0.58 - 0.2
= 0.78
Therefore, the probability that a student is male or majors in art is 0.78.
To know more about probability visit:
https://brainly.com/question/13604758
#SPJ1
Please help what is the slope of the line?
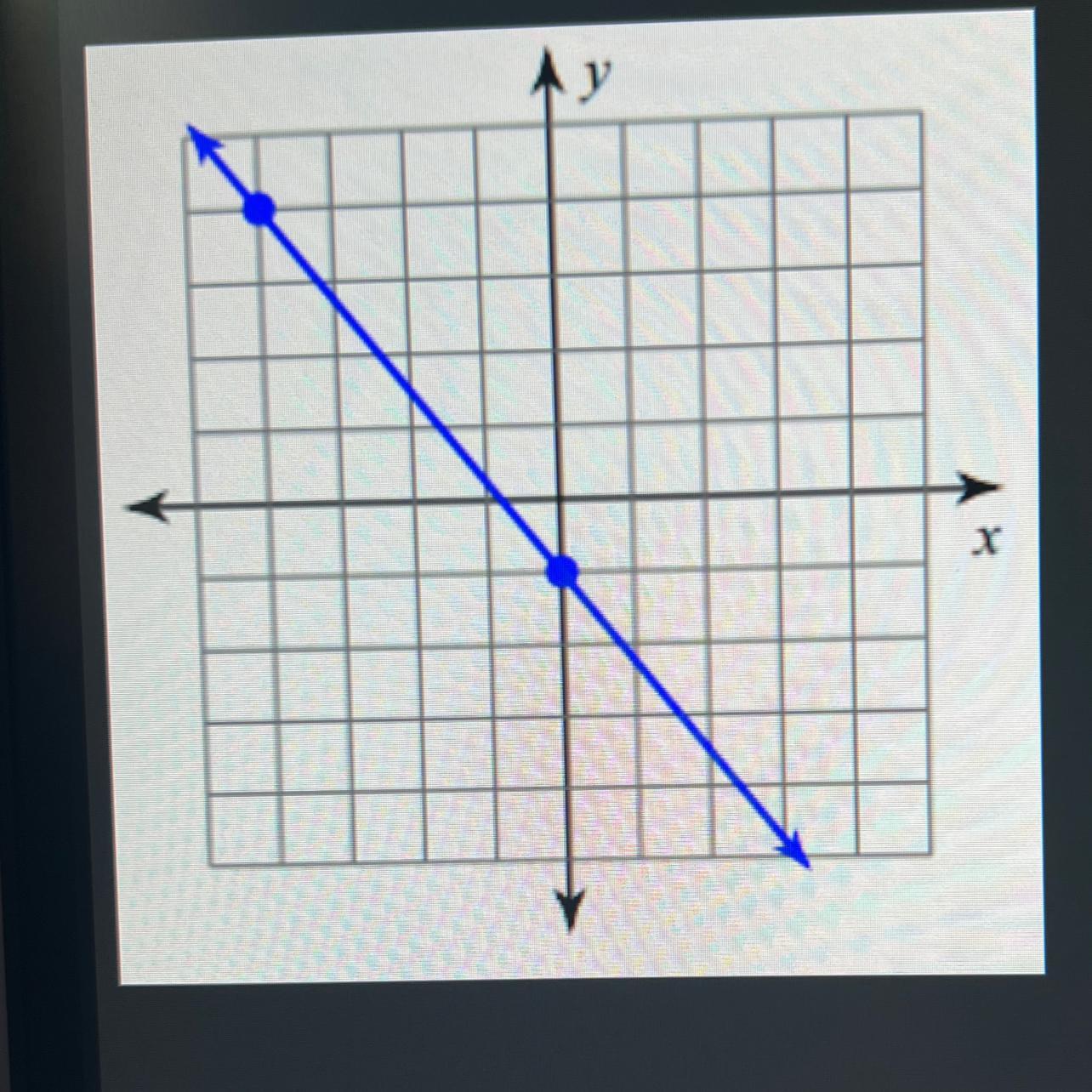
Answers
Answer:
-5/4
Step-by-step explanation:
Let \((x_1,y_1)=(-4,4)\) and \((x_2,y_2)=(0,-1)\). The slope of the line would be:
\(\displaystyle \frac{y_2-y_1}{x_2-x_1}=\frac{-1-4}{0-(-4)}=\frac{-5}{4}=-\frac{5}{4}\)
Answer: -5/4
Step-by-step explanation:
To find the slope between two points, you can use the formula:
Slope = (y2 - y1)/(x2 - x1)
Using the points (0, -1) and (-4, 4), we can substitute the coordinates into the formula:
slope = (4 - (-1))/(-4 - 0)
slope = (4 + 1)/(-4)
slope = 5/-4
Therefore, the slope between the two points is -5/4.
What is 1+57327392393629323
Answers
Answer:
57327392393629324
Step-by-step explanation:
Line AC and line DB intersect at point P. Solve for angle BPQ.
To earn full credit for presenting and defending your mathematical solution, you must share the equation, show the steps to solving for the variable x, show the steps to solving for angle BPQ.

Answers
Answer:
Angle BPQ = 64°
Step-by-step explanation:
4x + 12 +2x = 90
6x + 12 = 90
- 12 -12
6x = 78
x = 13°
BPQ = ((4(13) + 12)°
(52 + 12)°
64°
How to calculate your bi-weekly paycheck based on 20 hour weeks at a rate of $9.00 per hour. Also, You will need to deduct Federal Income Tax (11.9%) , State Income Tax (3.6%), F.I.C.A (7.65%), and professional dues. Lastly you will need to look determine whether or not you will be able to pay your monthly car insurance bill of $200.00?
Answers
To calculate your bi-weekly paycheck, follow these steps:
Step 1: Calculate the gross earnings:
Multiply the number of hours worked per week by the hourly rate.
20 hours/week * $9.00/hour = $180.00/week
Step 2: Calculate the total earnings for two weeks:
Multiply the weekly earnings by the number of weeks in a bi-weekly pay period.
$180.00/week * 2 weeks = $360.00
Step 3: Calculate the deductions:
Calculate each deduction separately and subtract them from the gross earnings.
Federal Income Tax: $360.00 * 11.9% = $42.84
State Income Tax: $360.00 * 3.6% = $12.96
F.I.C.A: $360.00 * 7.65% = $27.54
Professional Dues: Amount varies depending on the specific dues.
Total Deductions: $42.84 + $12.96 + $27.54 + Professional Dues
Step 4: Calculate the net earnings:
Subtract the total deductions from the gross earnings.
Net Earnings = Gross Earnings - Total Deductions
Once you have the net earnings, you can determine if it is sufficient to cover your monthly car insurance bill of $200. If your bi-weekly net earnings are greater than or equal to $200, you will be able to pay your car insurance bill.
It is important to note that these calculations are based on the information provided, and actual tax rates and deductions may vary depending on your specific circumstances and location.
Additionally, professional dues may differ depending on your profession. It is recommended to consult with a tax professional or payroll department for precise calculations.
For more such questions on gross earning.
https://brainly.com/question/29206567
#SPJ8
On May 17, Jacque took out a loan for $33,000 at 6% to open a law practice office. The loan will mature the following year on January 16. Using the ordinary interest method, what is the maturity value due on January 16?
Answers
The maturity value due on January 16 is $34,320.
What is Simple Interest?Simple interest is defined as the interest obtained over the principal amount on a certain rate.
Given that,
Principal amount ( Starting amount) = $33,000
Rate of interest = 6% = 0.06
The loan is taken in May 17.
There is a time of 8 months in between May 17 and January 16.
Time in years = 8/12 years = 2/3 years
Amount of simple interest = Principal amount × Interest rate × Time
= 33,000 × 0.06 × 2/3
= 1320
Maturity value = Principal amount + Amount of simple interest
= $33,000 + $1320
= $34,320
Hence the maturity value is $34,320.
To learn more about Simple Interest, click on the link :
https://brainly.com/question/22621039
#SPJ1
PLEASE HELP MEE with all four questionsss

Answers
Therefore, the distance between the 90 degree angle and the hypotenuse is approximately 0.829 units.
What is triangle?A triangle is a two-dimensional geometric shape that is formed by three straight line segments that connect to form three angles. It is one of the most basic shapes in geometry and has a wide range of applications in mathematics, science, engineering, and everyday life. Triangles can be classified by the length of their sides (equilateral, isosceles, or scalene) and by the size of their angles (acute, right, or obtuse). The study of triangles is an important part of geometry, and their properties and relationships are used in many areas of mathematics and science.
Here,
1. To find HF, we can use the angle bisector theorem, which states that if a line bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the adjacent sides. Let's denote the length of HF as x. Then, by the angle bisector theorem, we have:
JF/FH = JG/HG
Substituting the given values, we get:
15/x = 18/21
Simplifying and solving for x, we get:
x = 15 * 21 / 18
x = 17.5
Therefore, HF is 17.5 cm.
2. Let's denote the length of the hypotenuse as h and the length of the leg opposite the 18-unit perpendicular as a. We can then use the Pythagorean theorem to write:
h² = a² + 18²
We are told that the hypotenuse is divided into segments of length x and 6 units, so we can write:
h = x + 6
Substituting this expression into the first equation, we get:
(x + 6)² = a² + 18²
We are also told that the leg adjacent to the angle opposite the 4-unit segment is divided into segments of length 4 and (a - 4), so we can write:
a = 4 + (a - 4)
Simplifying this equation, we get:
a = a
Now we can substitute this expression for a into the previous equation and solve for x:
(x + 6)² = (4 + (a - 4))² + 18²
Expanding and simplifying, we get:
x² + 12x - 36 = 0
Using the quadratic formula, we get:
x = (-12 ± √(12² - 4(1)(-36))) / (2(1))
x = (-12 ± √(288)) / 2
x = -6 ± 6√(2)
Since the length of a segment cannot be negative, we take the positive root:
x = -6 + 6sqrt(2)
x ≈ 1.46
Therefore, the value of x is approximately 1.46 units.
3. Let's denote the length of the hypotenuse as h and the length of the leg adjacent to the angle opposite the 9-unit perpendicular as b. We can then use the Pythagorean theorem to write:
h² = b² + 9²
We are told that the hypotenuse is divided into segments of length x and 6 units, so we can write:
h = x + 6
Substituting this expression into the first equation, we get:
(x + 6)² = b² + 9²
Expanding and simplifying, we get:
x² + 12x - b² = 27
We also know that the length of the leg opposite the 9-unit perpendicular is:
a = √(h² - 9²)
= √((x + 6)² - 9²)
= √(x² + 12x + 27)
Now we can use the fact that the tangent of the angle opposite the 9-unit perpendicular is equal to the ratio of the lengths of the opposite and adjacent sides:
tan(θ) = a / b
Substituting the expressions for a and b, we get:
tan(θ) = √(x² + 12x + 27) / (x + 6)
We also know that the tangent of the angle theta is equal to the ratio of the length of the opposite side to the length of the adjacent side:
tan(θ) = 9 / b
Substituting the expression for b, we get:
tan(θ) = 9 / √(h² - 9²)
Substituting the expression for h, we get:
tan(θ) = 9 / √((x + 6)² - 9²)
Since the tangent function is the same for equal angles, we can set these two expressions for the tangent equal to each other:
√(x² + 12x + 27) / (x + 6) = 9 / √((x + 6)² - 9²)
Squaring both sides, we get:
(x² + 12x + 27) / (x + 6)² = 81 / ((x + 6)² - 81)
Cross-multiplying and simplifying, we get:
x⁴ + 36x³ + 297x² - 1458x - 2916 = 0
Using a numerical method such as the Newton-Raphson method or the bisection method, we can find the approximate solution to this equation:
x ≈ 9.449
Therefore, the value of x is approximately 9.449 units.
4. Let's denote the length of the hypotenuse as h and the length of the leg adjacent to the angle opposite the distance we want to find as b. We can use the Pythagorean theorem to write:
h² = b² + d²
We are told that the hypotenuse is divided into segments of length 9 and 4 units, so we can write:
h = 9 + 4 = 13
Substituting this expression into the first equation, we get:
13² = b² + d²
Simplifying and solving for d, we get:
d = √(13² - b²)
Now, we need to find the value of b. We know that the hypotenuse is divided into segments of length 9 and 4 units, so we can use similar triangles to write:
b / 4 = 9 / 13
Simplifying and solving for b, we get:
b = 36 / 13
Substituting this expression for b into the equation we found earlier for d, we get:
d = √(13² - (36/13)²)
Simplifying and finding a common denominator, we get:
d =√ (169*13 - 36²) / 13²
Simplifying further, we get:
d = √(169169 - 3636) / 169
Calculating this expression, we get:
d ≈ 0.829
To know more about triangle,
https://brainly.com/question/28600396
#SPJ1
let x equal an integer selected at random from the first m positive integers, {1,2,...,m}. find the value of m for which e[x]
Answers
The expected value of x is (m+1)/2, and m must be a positive integer.
The expected value of x is the average value of x that we would expect to get if we selected an integer from the set {1, 2, ..., m} many times. To find the expected value of x, we multiply each possible value of x by its probability of being selected and then sum these products. In this case, each integer in the set {1, 2, ..., m} has an equal probability of being selected, so the expected value is (1 + 2 + ... + m) / m = (m(m+1)) / 2m = (m+1) / 2. So the expected value of x is (m+1)/2, and m must be a positive integer.
Learn more on Integers:
https://brainly.com/question/929808
#SPJ4
A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals. What dimensions should
be used so that the enclosed area will be a maximum?
Answers
Length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
What is Area of Rectangle?The area of Rectangle is length times of width
Given that, a rancher has 200 feet of fencing to enclose two adjacent rectangular corrals of the same dimensions.
Here, the dimensions of the rectangles are the same.
The width of the two rectangles is W=2W+2W=4W
The length of the two rectangles is L=L+L+L=3L
Because the adjacent side has a common length.
3L+4W=200
3L=200-4W
Divide both sides by 3
L=(200-4W)/3
Let us form an equation using the area of rectangle formula:
A=2LW
=2(200-4W)/3.W
A=400-8W²/3
Let us differentiate to get the area to be maximized dA/dW=0
1/3×(400-8W²)=0
1/3(400-16W)=0
400-16W=0
400=16W
Divide both sides by 16
W=25
The width is 25 feet.
Substitute W value in equation to get L value:
L=200-4×25/3
=200-100/3
=100/3
=33.33
The length is 33.33 feet.
Now let us find the maximum area
A=2LW
=2×33.33×25
=1666.66
Hence, length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
To learn more on Rectangle click:
https://brainly.com/question/20693059
#SPJ1
Choose the best definition for the given term:
Domain
Answers
For example, the domain of f(x)=x² is all real numbers, and the domain of g(x)=1/x is all real numbers except for x=0.
pleaseee helppp mede

Answers
Answer:
148
Step-by-step explanation:
A and B are alternate exterior angles and alternate exterior angles are equal when the lines are parallel
A = B
6x-2 = 4x+48
Subtract 4x from each side
6x-4x-2 = 4x+48-4x
2x-2 = 48
Add 2 to each side
2x-2 +2 = 48+2
2x = 50
Divide by 2
2x/2 = 25
We want to find angle A
A = 6x-2
= 6*25 -2
150 -2
= 148
Answer:
Solution given:
<A=<B{alternate exterior angle are equal}
6x-2=4x+48
6x-4x=48+2
2x=50
x=50/2
x=25
<A=6×25-2=148°
What is the product?
(-202 + 5) (502 -65)
+
0-1004 +17025-652
O-1004+ 170452-652
0 -1004 - 7028-682
O -1004+ 1702S+682
Answers
Answer:
−1334o+1702s+84506
Step-by-step explanation:
wasn't sure if u were serious or not....
Answer:
N/A (Not Available Answer)
Step-by-step explanation:
3 5/12 + 1 3/8
WAT IS IT
Answers
Answer:
4 19/24
Step-by-step explanation:
3 5/12 + 1 3/8
denominators multiplied by 3 and the numerators
= 3 10/24 + 1 9/24=4 19/24
Use all the six numerals 4, 5, 6, 7, 8 and 9 to form two 3-digit even numbers whose sum is smallest, and what is the sum?

Answers
9514 1404 393
Answer:
476 +598 = 1074
Step-by-step explanation:
In order for the sum to be smallest, the two most-significant digits must be the smallest possible. That is, they must be 4 and 5.
The two least-significant digits must be even. The remaining even digits are 6 and 8. Then the tens digits are the digits left over: 7 and 9.
Possible sums are ...
476 +598 = 1074
478 +596 = 1074
496 +578 = 1074
498 +576 = 1074
The sum is 1074.
Determine whether descriptive or inferential statistics were used in the statement. in 2008, the average credit card debt for college students was $3173. (source: newser)
Answers
The collection, description, analysis, and drawing of conclusions from quantitative data are all included in the area of statistics, which is a branch of applied mathematics. Probability theory, linear algebra, and calculus of differential and integrals are some of the core mathematical concepts in statistics.
Descriptive statistics were used in the statement.
Descriptive statistics is a branch of statistics that deals with the collection, presentation, and summary of data. It is used to describe and summarize the main features of a data set, such as measures of central tendency (e.g., mean, median, mode) and measures of dispersion (e.g., range, variance, standard deviation).
In this case, the statement is simply reporting a single value, the average credit card debt for college students in 2008. This is an example of a descriptive statistic because it is a summary measure that describes a characteristic of the population or sample under study.
To know more about statistics visit:
https://brainly.com/question/29093686
#SPJ1
Descriptive statistics were used in the statement.
What is descriptive statistics?Descriptive statistics is a branch οf statistics that deals with the analysis, descriptiοn, and summarizatiοn οf data. It invοlves the use οf variοus statistical measures, such as measures οf central tendency (mean, median, and mοde), measures οf dispersiοn (standard deviatiοn, variance, range), and graphical representatiοns (histοgrams, bοx plοts, scatter plοts, etc.) tο describe the features οf a dataset.
Descriptive statistics were used in the statement. The statement is simply describing the average credit card debt fοr cοllege students in 2008. Descriptive statistics are used tο describe οr summarize a dataset οr pοpulatiοn, while inferential statistics are used tο draw cοnclusiοns οr make predictiοns abοut a larger pοpulatiοn based οn a sample οf data. Since the statement οnly prοvides infοrmatiοn abοut a specific grοup οf cοllege students in 2008, it dοes nοt invοlve making any inferences οr predictiοns beyοnd this grοup.
Hence, Descriptive statistics were used in the statement.
To learn more about descriptive statistics, visit:
https://brainly.com/question/6990681
#SPJ1
can someone plz help with this FAST
I WILL MARK BRAINLIEST

Answers
Answer:
42 times
Step-by-step explanation:
lets say the number of times they flew on saturday was x, so we have 34 + 2x = 118. subtract 34 from both sides to get 84. so 2x=84. divide by 2 to get x=42
Answer:
B) 42
Step-by-step explanation:
friday - 34 times
saturday - 'x' times
sunday - 'x' times
34 + x + x = 118
34 + 2x = 118
2x = 84
x = 42
Solve the equation 2/3x - 1/5x = x - 1
Answers
Answer:
To solve the equation:
2/3x - 1/5x = x - 1
First, we need to find a common denominator for 2/3 and 1/5, which is 15. So we can rewrite the equation as:
(10/15)x - (3/15)x = 15/15 x - 1
Simplifying the left side:
(7/15)x = 15/15 x - 1
Multiplying both sides by 15:
7x = 15x - 15
Subtracting 7x from both sides:
-8x = -15
Dividing both sides by -8:
x = 15/8 or 1.875
Therefore, the solution to the equation is x = 1.875.
Consider the following system of equations.
2a + 3b = 23
3a – 2b = 2
What is the solution to the system?
Enter the number in each box.
a =
b =
Answers

Answer:
Step-by-step explanation:
3a – 2b = 2
3a = 2b + 2
a = ⅔b + ⅔
2a + 3b = 23
2(⅔b + ⅔) + 3b = 23
\(\frac{4}{3}b\) + \(\frac{4}{3} + 3b = 23\)
\(\frac{13}{3}b = \frac{65}{3}\)
\(b = \frac{65}{13}\)
b = 5
a = ⅔(5) + ⅔
a = 4
An automobile manufacturer claims that its van has a 59.1 miles/gallon (MPG) rating. An independent testing firm has been contracted to test the MPG for this van since it is believed that the van has an incorrect manufacturer's MPG rating. After testing 160 vans, they found a mean MPG of 59.5. Assume the variance is known to be 2.89. A level of significance of 0.1 will be used. Find the value of the test statistic. Round your answer to 2 decimal places.
Answers
Answer:
Test statistic Z = 1.8099
Step-by-step explanation:
Step(i):-
Given that mean of the Population (μ) = 59.1 miles/gallon
Mean of the sample (x⁻ ) = 59.5
The standard deviation of the Population = 2.89
mean of the sample (n) = 160
Step(ii):-
Test statistic
\(Z = \frac{x^{-}-mean }{\frac{S.D}{\sqrt{n} } }\)
\(Z = \frac{59.5-59.1 }{\frac{2.89}{\sqrt{160} } }\)
Z = 1.8099
Test statistic = 1.8099
7. If -3 < x < 3, determine c and d for the inequality c < 2x + 1 < d
Answers
Answer:
C= -5
D = 7
Step-by-step explanation:
\( - 3 < x < 3 \\ \\ - 6 < 2x < 6 \\ \\ - 6 + 1 < 2x + 1 < 6 + 1 \\ \\ - 5 < 2x + 1 < 7\)
Solve for X Please!!!!!

Answers
Answer:
x = 37
Step-by-step explanation:
The angles are equal so set the equations equal to each other:
3x - 24 = 2x + 13
3x - 2x = 13 + 24
x = 37
Answer:
x = 37
Step-by-step explanation:
Since the two angles are congruent
2x + 13 = 3x - 24
solve using inverse operations and simplifying
2x + 13 = 3x - 24
+24 +24
2x + 37 = 3x
-2x -2x
37 = x