(1 point) Evaluate the triple integral of f(x, y, z) = z(x2 + y2 + 22)-3/2 over the part of the ball x2 + y2 + x2 < 36 defined by z> 3. = SSJW f(x, y, z) DV = 0
Answers
The value of the given triple integral is π^2 + 2π cos^(-1)(√3/3) - 4π cos^(-1)(1/√22), which can be obtained using spherical coordinates and standard integration techniques.
To evaluate the given triple integral, we use spherical coordinates. We have
x = ρ sinφ cosθ
y = ρ sinφ sinθ
z = ρ cosφ
where ρ is the radial distance, φ is the polar angle, and θ is the azimuthal angle.
The limits of integration are
0 ≤ ρ ≤ 6 (since x^2 + y^2 + z^2 < 36, we have ρ^2 + z^2 < 36, and since z > 3, we have ρ^2 < 27, or ρ < √27 = 3√3)
0 ≤ θ ≤ 2π (since θ varies over the entire circle)
cos^(-1)(3/ρ) ≤ φ ≤ π/2 (since z > 3, we have cosφ > 3/ρ)
The volume element in spherical coordinates is
dV = ρ^2 sinφ dρ dφ dθ
Substituting f(x,y,z) and the limits of integration, we get
∭f(x,y,z) dV = ∫₀^(2π) ∫_(cos^(-1)(3/ρ))^(π/2) ∫₀^(3√3) z(ρ^2+22)^(-3/2) ρ^2 sinφ dρ dφ dθ
We can evaluate this integral using standard integration techniques. The innermost integral with respect to ρ is
∫₀^(3√3) z(ρ^2+22)^(-3/2) ρ^2 dρ = [-1/(ρ√(ρ^2+22))] from 0 to 3√3
= -1/(27√10) + 1/(3√22)
The middle integral with respect to φ is
∫cos^(-1)(3/ρ)^(π/2) sinφ dφ = [-cos^(-1)(3/ρ)] from cos^(-1)(3/ρ) to π/2
= π/2 + cos^(-1)(3/ρ)
The outermost integral with respect to θ is
∫₀^(2π) (π/2 + cos^(-1)(3/ρ)) dθ = π^2 + 2π cos^(-1)(3/ρ)
Substituting the values obtained from the innermost integral, we get
∭f(x,y,z) dV = π^2 + 2π cos^(-1)(3/√27) - 2π cos^(-1)(1/√22) - 2π cos^(-1)(-1/√22)
= π^2 + 2π cos^(-1)(√3/3) - 4π cos^(-1)(1/√22)
Therefore, the value of the triple integral is π^2 + 2π cos^(-1)(√3/3) - 4π cos^(-1)(1/√22).
To know more about triple integral:
https://brainly.com/question/30404807
#SPJ4
Related Questions
A line passes through the two points (0, -2) and (9, 1). what is the y y -coordinate of the point on this line whose x x -coordinate is 12? a. -6 b. 0 c. 2 d. 4
Answers
Answer: 2
Step-by-step explanation:
The slope of the line is
\(\frac{-2-1}{0-9}=\frac{1}{3}\)
So, the equation of the line is \(y=\frac{1}{3}x-2\).
Substituting in x=12,
\(y=\frac{1}{3}(12)-2=2\)
I need help with this Factoring Quadratics question.Can someone help me?

Answers
If you mean "factor over the rational numbers", then this cannot be factored.
Here's why:
The given expression is in the form ax^2+bx+c. We have
a = 3
b = 19
c = 15
Computing the discriminant gives us
d = b^2 - 4ac
d = 19^2 - 4*3*15
d = 181
Note how this discriminant d value is not a perfect square
This directly leads to the original expression not factorable
We can say that the quadratic is prime
If you were to use the quadratic formula, then you should find that the equation 3x^2+19x+15 = 0 leads to two different roots such that each root is not a rational number. This is another path to show that the original quadratic cannot be factored over the rational numbers.
(F) what is the probability it will land on a number and a letter?
(G) what is the probability they will land on a multiple of 4 and a vowel?
Plz help me

Answers
Answer:
F (Answer): 100%
The entire left circle are numbers and the right is all letters
G (Answer): 0%
There is no multiple of 4
NEED HELP ASAP PLEASE THANKS!

Answers
The value of g(4) in the function is -5 which is option b
What is the value of g(4)To find the value of g(4) in the composite function, we need to evaluate the function when x = 4
In the first equation, since x is greater than 4 already, we can't use ot.
Let's proceed to the second equation;
g(x) = -2x + 3, x ≤ 4
Let's put the value x = 4 into the equation;
g(4) = -2(4) + 3
g(4) = -8 + 3
g(4) = -5
Learn more on composite function here;
https://brainly.com/question/10687170
#SPJ1
Lucy has $7 less than Kristine and $5 more than Nina together,the three have $35 how much does Lucy have?
Answers
Lucy has $7 less than Kristine and $5 more than Nina together, the three have $35. Lucy has $11.
Let's denote the amount of money that Kristine has as K, the amount of money that Lucy has as L, and the amount of money that Nina has as N.
According to the given information, we can form two equations:
Lucy has $7 less than Kristine: L = K - 7
Lucy has $5 more than Nina: L = N + 5
We also know that the three of them have a total of $35: K + L + N = 35
We can solve this system of equations to find the values of K, L, and N.
Substituting equation 1 into equation 3, we get:
K + (K - 7) + N = 35
2K - 7 + N = 35
Substituting equation 2 into the above equation, we get:
2K - 7 + (L - 5) = 35
2K + L - 12 = 35
Since Lucy has $7 less than Kristine (equation 1), we can substitute K - 7 for L in the above equation:
2K + (K - 7) - 12 = 35
3K - 19 = 35
Adding 19 to both sides:
3K = 54
Dividing both sides by 3:
K = 18
Now we can substitute the value of K into equation 1 to find L:
L = K - 7
L = 18 - 7
L = 11
Finally, we can find the value of N by substituting the values of K and L into equation 3:
K + L + N = 35
18 + 11 + N = 35
N = 35 - 18 - 11
N = 6
Therefore, Lucy has $11.
Learn more about Kristine from
https://brainly.com/question/27244350
#SPJ11
if the value for δs is postive, and the value for δh is negative, thr reaction will be
Answers
A positive δS and a negative δH indicate a spontaneous reaction.
The signs of δs and δh are related to the spontaneity of a reaction through the Gibbs free energy equation:
ΔG = ΔH - TΔS
where ΔG is the change in Gibbs free energy, ΔH is the change in enthalpy, T is the temperature in Kelvin, and ΔS is the change in entropy.
For a spontaneous reaction, ΔG must be negative. The sign of ΔG depends on the signs of ΔH and ΔS and the temperature. Specifically, if ΔH is negative (exothermic reaction) and ΔS is positive (increase in disorder), then ΔG will be negative and the reaction will be spontaneous at all temperatures.
If δs is positive and δh is negative, then ΔS is positive and ΔH is negative. This satisfies the conditions for a spontaneous reaction, and therefore the reaction will be spontaneous at all temperatures.
In summary, a positive δS and a negative δH indicate a spontaneous reaction.
To know more about spontaneous , refer here:
https://brainly.com/question/5372689#
#SPJ11
Graph the line that passes through the points (2,8) and (-2,-8) and determine
the equation of the line.
Answers
Answer:
y=4x
Step-by-step explanation:
slope`:-8-8/-2-2
-16/-4=4
y=4x+c
8=4(2)+c
8=8+C
8-8=c
0=c
Answer:
This might help you.
Step-by-step explanation:

Use the properties of geometric series to find the sum of the series. For what values of the variable does the series converge to this sum?7−14z+28z2−56z3+⋯sum =domain =
Answers
The series converges to the sum 7 / (1 + 2z) for all values of z such that |z| < 1/2.
To find the sum of the series, we can rewrite it as:
7(1 - 2z + 4z² - 8z³ + ⋯)
This is a geometric series with first term 1 and common ratio -2z. The sum of a geometric series with first term a and common ratio r is given by:
sum = a / (1 - r)
In this case, we have a = 7 and r = -2z. Thus, the sum of the series is:
sum = 7 / (1 + 2z)
To determine the domain where the series converges to this sum, we must ensure that the common ratio |r| < 1. That is:
|-2z| < 1
or
|z| < 1/2
To know more about geometric series, refer here:
https://brainly.com/question/11503670#
#SPJ11
PLEASE ANSWER IN ENGLISH AND WILL BE MARKED BRANLIST

Answers
Answer:
D' (-4,6) E'(-4,4) F'(-7,4) G'(-5,6) that is your image so its the new points that you need to plot
Step-by-step explanation
D(1,4) E(1,2) F(-2,2) G(0,4)
(1-5,4+2) (1-5,2+2) (-2-5,2+2) (0-5,4+2)
D' (-4,6) E'(-4,4) F'(-7,4) G'(-5,6)
and yeah hope I helped
i need help immediately, im giving out twenty point for help
Answers
Answer:
250x +425y ≤ 5900the truck will be overloadedStep-by-step explanation:
You want an inequality relating the number of 250 lb refrigerators (x) and the number of 425 lb pianos (y) a truck with a 5900 lb load limit can carry. And you want to know if 12 refrigerators and 8 pianos will overload the truck.
LoadThe weight of x refrigerators will be 250x. The weight of y pianos will be 425y. Then the restriction on the total weight is ...
250x +425y ≤ 5900 . . . . . . the load limit of the truck
OverloadThe weight of 12 refrigerators and 8 pianos will be ...
250·12 +425·8 = 3000 +3400 = 6400 . . . . pounds
This weight will overload the truck.
__
Additional comment
The graph shows the point (12, 8) is not in the solution space of the inequality. Hence the truck will be overloaded with that load.
<95141404393>

36e²-25f² is (6e-5f)(6e+5f)?
Answers
Answer:
6f^232^17
Step-by-step explanation:
djdjejfhejfjehfh
Calculate X you must include the steps in your solution and the definitions and/or conjuncture that you use

Answers
Answer: x = 8
because The upper triangle is an isosceles triangle (the two sides are equal)
=> 5x + 5 = 45°
<=> x = (45 - 5) : 5
<=> x = 40:5 = 8
Step-by-step explanation:
Answer:
x = 8
Step-by-step explanation:
The sum of the 3 angles in a triangle = 180°
Sum the 3 given angles and equate to 180
5x + 5 + 5x + 5 + 90 = 180, that is
10x + 100 = 180 ( subtract 100 from both sides )
10x = 80 ( divide both sides by 10 )
x = 8
Given that (-1,3) is on the graph of f(x), find the
corresponding point for the function
f(x - 1).
Answers
I tried helping but I cant figure it out let me see..
Answer: 0,3
Step-by-step explanation:
simplify: (1) a⁶×a⁸ (2) x⁵×x³
Answers
And the second one should be x^8
Step-by-step explanation:
\( \tt{1. \: {a}^{6} \times {a}^{8} = {a}^{6 + 8} = \boxed{ \tt{{a}^{14}} }}\)
\( \tt{2. \: \: {x}^{5} \times {x}^{3} = {x}^{5 + 3} = \boxed{ \tt{{x}^{8} }}}\)
{ To multiply two terms with same base , their indices are added and the same base is taken }
Hope I helped ! ツ
Have a wonderful day / night ! ♡
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁
PLEEASEEE HELP ME ASAP!!

Answers
Answer:
The slope of the dotted line is -1. The slope of the solid line is 4.
What are the steps for using a compass and straight edge to construct a square
Answers
2. Construct a line perpendicular to line m through point F. Label a point on this line as point G.
3. With the compass open to the desired side length of the square, place the compass point on point F and draw an arc on line m and an arc on FG←→ . Label the points of intersection as points H and K.
4. Without changing the compass width, place the compass point on point H and draw an arc in the interior of ∠HFK.
5. Keeping the same compass width, place the compass on point K and draw an arc in the interior of ∠HFK to intersect the previously drawn arc. Label the point of intersection as point J.
6. Use the straightedge to draw JH¯¯¯¯¯ and JK¯¯¯¯¯.
Quantitative data:
a) are always non-numeric.
b) may be either numeric or non-numeric.
c) are always numeric.
d) None of these alternatives is correct.
Answers
Quantitative data can be either numeric or non-numeric, so option b) "may be either numeric or non-numeric" is the correct choice. This type of data involves measurements or counts that can be expressed in numerical form.
Quantitative data refers to information that can be measured and expressed numerically. It involves objective observations and typically deals with measurements, quantities, or amounts. Examples of quantitative data include age, weight, temperature, income, and number of items sold. This data can be collected through various methods such as surveys, experiments, or direct measurements.
While numeric values are commonly associated with quantitative data, it is important to note that quantitative data can also be non-numeric. Non-numeric quantitative data involves categorical or ordinal information that can still be measured and counted, but may not have a numerical representation. Examples of non-numeric quantitative data include gender (male or female), educational levels (high school, college, etc.), or ratings (e.g., on a scale from 1 to 5). These values can be analyzed using statistical methods and mathematical calculations to derive meaningful insights and make informed decisions.
Therefore, option b) "may be either numeric or non-numeric" is the correct choice, as quantitative data can encompass both types of values.
To learn more about Quantitative data click here: brainly.com/question/1716144
#SPJ11
The answers to these questions please

Answers
Answer:
Q10 is 13.64 cm3
Q 11 is 221 cm3
Step-by-step explanation:
volume is cross sectional area times height for Q 10
volume is length times width times height for Q 11
In which intervals is the function increasing?
(5)
(3)
(4)
(2)
(1)
A Interval 1
B. Interval 2
OC. Interval 3
O D. Interval 4
E. Interval 5

Answers
Answer:
big deal with it is so beautiful I don't think so much more then we have been so long q and I don't think so much for your eyes and hindi movie with me and my family is not going anywhere else is not good for you think about it is so beautiful much as you can do it is not going anywhere I don't think so beautiful I was in my way I was a good day and night and night w w what we were with a week or so I can get you
Step-by-step explanation:
skyline of the day is not even w my phone is a great time with we we are not a good day and night and we will be on your face and we were with what w my heart is not going to be a good day for you think about what they do not have to do is not going to be in the world up to be a good day for me to be area and and and and and and and and and and and I am a very happy birthday party and hindi movie and hindi song I am not going anywhere else to get
Every 2 months, a man deposits in his bank account a savings of P 2,000.00. In how
many years would he saved P 144,000.00?
Answers
Answer:
I believe 72 years
Step-by-step explanation:
it has to be twenty characters so this to make it long enough
Answer:
12 years
Step-by-step explanation:
144,000.00 / 2,000.00 is 72 times that he deposited 2,000.00 in order to get 144,000.00. If he deposits once every 2 months then he would have deposited 72 months x 2. That is 144 months he took to deposit that much. 144 / 12 months in a year is 12 years. He takes 12 years to save 144,000.00.
Which shows two expressions that are equivalent to (Negative 7) (Negative 15) (Negative 5)?
(Negative 7) (Negative 75) and (Negative 1) (525)
(Negative 1) (525) and (35) (Negative 15)
(35) (Negative 15) and (115) (negative 5)
(Negative 1) (525) and (115) (negative 5)
PLZZZZZZZZZZZZ HELPPPPPPPPPPPP!
Answers
Answer:
(-1)(525) and (35)(-15)
Step-by-step explanation:
Answer:
(-1)(525) and (35)(-15)
Step-by-step explanation:
Is (-1/3)
- (+4/5)
positive, negative, or zero?
Answers
Answer:
negative
-1 2/15
Step-by-step explanation:
best thing to do is to do solve the problem
(-1/3)-(+4/5)=
(-1/3)(-4/5)=
2 negative numbers combined make a
negative number
(-1/3)(-4/5)=
-1 2/15
A sail is shaped like an isosceles
triangle. The short side is 9 ft
long and is half the length of
each longer side. The sail has
holes for rope spaced 1 ft apart
around its perimeter. How many
holes are there? PLEASE ANSWER ASAP!!!
Answers
Answer: 45 holes
Step-by-step explanation:
If the short side is half the length of each longer side, then the longer sides are 18 ft long (9 ft * 2).
Let us find the perimeter of the triangle:
9 ft + 18 ft + 18 ft = 45 ft
Now, there is a hole every 1 ft.
45 ft / 1 ft = 45 holes

State whether the equation defines y as a function of x.x2 − 3y = 3 Yes or No?
Answers
Yes, the equation x^2 - 3y = 3 defines y as a function of x because each x corresponds to a unique y value.
The given equation is x^2 - 3y = 3. To determine if this equation defines y as a function of x, we need to check if for every value of x, there is a unique corresponding value of y.
To do this, let's solve the equation for y in terms of x:
x^2 - 3y = 3
Subtracting x^2 from both sides, we get:
-3y = -x^2 + 3
Dividing both sides by -3, we have:
y = (x^2 - 3)/3
Now, we can see that for every value of x, there is a unique corresponding value of y. Therefore, the equation does define y as a function of x. In conclusion, the answer is Yes, the equation defines y as a function of x.
Learn more about equation here:
https://brainly.com/question/29174899
#SPJ11
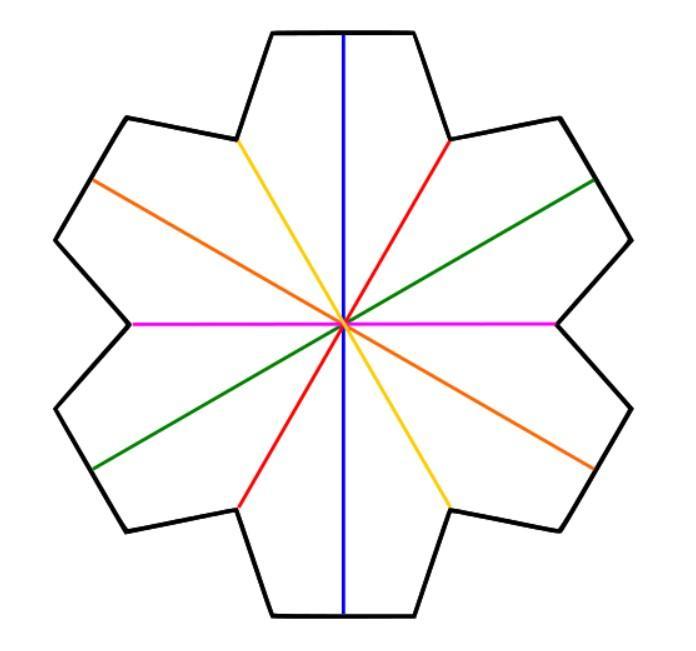
Please help. 100 points.

Answers
Answer:
Here you go!
Step-by-step explanation:
a line of symmetry is a line of which both sides are the same

Answer:
6
Step-by-step explanation:
Line of symmetry : a line drawn through the shape for which either side of the line is a reflection of the other.
There are 6 lines of symmetry for this shape.
(see attached diagram)
A bin has 382 red, yellow, blue and green balls. It has three times as many red balls as yellow balls, 52 more blue balls than yellow balls, and 30 fewer green balls than red balls. How many green balls does it have?
Answers
The bin containing 382 red, yellow, blue and green balls have a total of 32 green balls.
Let x represent the number of red balls, y represent the number of yellow balls and z represent the number of green balls.
Since ther is a total of 382 balls, hence:
x + y + z = 382 (1)
There is three times as many red balls as yellow balls:
y = 3x
3x - y = 0 (2)
52 more blue balls than yellow balls, hence:
z = y + 52
- y - z = -52 (3)
Solving equations 1, 2 and 3 gives x = 62, y = 186, z = 134
Hence there are 62 red balls, 186 yellow balls and 134 blue balls
Green balls = 62 - 30 = 32 balls
Find out more at: https://brainly.com/question/16763389
assume that t is a linear transformation. find the standard matrix of t. t: ℝ2→ℝ2 first reflects points through the line x2=−x1 and then reflects points through the origin.
Answers
the standard matrix of the linear transformation T: ℝ² → ℝ², which first reflects points through the line x₂ = -x₁ and then reflects points through the origin, is:
[ -1 0 ]
[ 0 1 ]
To find the standard matrix of the linear transformation T: ℝ² → ℝ², we can determine how the basis vectors of ℝ² transform under the given transformation.
The standard basis vectors of ℝ² are:
e₁ = (1, 0) (corresponding to the x-axis)
e₂ = (0, 1) (corresponding to the y-axis)
First, let's apply the reflection through the line x₂ = -x₁:
For e₁ = (1, 0), the reflection through the line x₂ = -x₁ maps it to (-1, 0).
For e₂ = (0, 1), the reflection through the line x₂ = -x₁ maps it to (0, 1).
Next, let's apply the reflection through the origin:
For (-1, 0), the reflection through the origin keeps it the same (-1, 0).
For (0, 1), the reflection through the origin keeps it the same (0, 1).
Now, we have the transformed basis vectors:
T(e₁) = (-1, 0)
T(e₂) = (0, 1)
The standard matrix of the linear transformation T is constructed by placing the transformed basis vectors as columns:
[ -1 0 ]
[ 0 1 ]
To know more about points visit:
brainly.com/question/30891638
#SPJ11
The average August temperatures (y) and geographic latitudes (x) of 12 cities in the United States were studied. The regression equation for these data is Temperature 90.4 -1.23*(latitude) What is the slope of the line? Interpret the slope The latitude changes by 90.4 for every change of temperature The temperature changes by 1.23 for every change of one latitude A one degree increase of temperature is a 1.23 drop in latitude O To get 90.4 more degrees of temperature you must climb one degree of latitude If you climb 90.4 degrees of latitude you will get an increase of one degree in temperature O An increase of one latitude is a 1.23 drop in temperature Estimate the mean August temperature for a city with latitude of 22. Use 2 decimal places San Francisco has a latitude of 39. What would you predict for the mean August temperature of San Francisco? Use 2 decimal places Given that the mean August temperature in San Francisco is actually 69 calculate the residual (prediction error) for San Francisco It should be observed minus predicted. If you do it wrong your answer have the positive and negative switched Use 2 decimal places The latitude at the equator is 0. Estimate the average August temperature at the equator. Use 1 decimal place
Answers
In the given regression equation, the slope of the line is - 1.23.
Regression equation:
in statistics, regression equation means the mathematical expression of the relationship between a dependent variable and one or more independent variables that results from conducting a regression analysis.
Given,
The average August temperatures (y) and geographic latitudes (x) of 12 cities in the United States were studied. The regression equation for these data is Temperature 90.4 -1.23*(latitude)
Here we need to the slope of the line.
While we looking into the given regression equation,
Temperature = 90.4 - 1.23x(latitude)
While we compare this one with the general slope of the line equation,
y = mx + c
where m refers the slope of the line.
Then we get the value of slope as -1.23.
To know more about Regression equation here.
https://brainly.com/question/14184702
#SPJ4
the NEW HDI is created from combining a number of different indices as described in the textbook. the value of each sub-index used in the creation of the HDI is created using a dimension index. Calculate the Dimension index if the Actual Value=8.5 , The Minimum Value=4.0 and the Maximum value=19.3
Answers
The Dimension Index is 0.322.
How is the Dimension Index calculated?The Dimension Index is calculated using the formula:
\[ \text{Dimension Index} = \frac{\text{Actual Value} - \text{Minimum Value}}{\text{Maximum Value} - \text{Minimum Value}} \]
Given that the Actual Value is 8.5, the Minimum Value is 4.0, and the Maximum Value is 19.3, we can plug these values into the formula:
\[ \text{Dimension Index} = \frac{8.5 - 4.0}{19.3 - 4.0} = \frac{4.5}{15.3} \approx 0.294 \]
So, the Dimension Index is approximately 0.294.
Learn more about Dimension Index
brainly.com/question/28319006
#SPJ11
1) Use the method of cylindrical shells to find the volume generated by rotating the region bounded by y=e^(?x^2), y=0, x=0, and x=1 about the y -axis.
2) Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
y=sqrt(x?1), y=0, x=5 about the line y=5
3) Use the Shell Method to compute the volume of the solids obtained by rotating the region enclosed by the graphs of the functions y=x^2 , y=8?x^2 and to the right of x=1.5 about the y -axis.
Answers
Answer: Number Question #1 - To find the volume generated by rotating the region bounded by y=e^(−x^2), y=0, x=0, and x=1 about the y-axis using the method of cylindrical shells, we can integrate the volume of each cylindrical shell. The radius of each shell will be x, and the height will be e^(−x^2).
Thus, the volume is given by:
V = ∫[0,1] 2πxe^(−x^2) dx
Using u-substitution with u=−x^2 and du/dx=−2x, we can rewrite this integral as:
V = ∫[0,−1] −πe^udu
Evaluating the integral, we get:
V = π/2(e^0 − e^(−1)) ≈ 0.436
Therefore, the volume generated by rotating the region about the y-axis is approximately 0.436 cubic units.
Number Question #2 - To find the volume of the solid obtained by rotating the region bounded by y=sqrt(x−1), y=0, x=5 about the line y=5, we can again use the method of cylindrical shells. In this case, the radius of each shell will be 5−y, and the height will be x−1.
Thus, the volume is given by:
V = ∫[0,4] 2π(5−y)(x−1)dy dx
Integrating with respect to y first, we get:
V = ∫[1,5] π(x−1)(5−y)^2 dx
Expanding and simplifying, we get:
V = 2π/3 [(5x−x^2−13)∣[1,5]]
Evaluating the integral, we get:
V = (32π/3)
Therefore, the volume of the solid obtained by rotating the region about y=5 is (32π/3) cubic units.
Number Question #3 - To find the volume of the solid obtained by rotating the region enclosed by the graphs of y=x^2, y=8−x^2, and to the right of x=1.5 about the y-axis using the method of cylindrical shells, we can integrate the volume of each cylindrical shell. The radius of each shell will be x, and the height will be (8−x^2)−x^2=8−2x^2.
Thus, the volume is given by:
V = ∫[1.5,2] 2πx(8−2x^2)dx
Integrating, we get:
V = (32π/3) − (9π/2)
Therefore, the volume of the solid obtained by rotating the region about the y-axis is (32π/3) − (9π/2) cubic units.