10) -6x + 8y = 0
-3x + 4y = 2
Infinite solution or no solution
Answers
Related Questions
Harper uploaded a funny video of her dog onto a website.
The relationship between the elapsed time, tea, in days since the videos first uploaded, and the total number of views, V(d) that the video received is modeled by the following function
V(d)=4^1.25d
How many views will the video receive after 6 days ? Round the answer to the nearest hundredth
Answers
Answer:
32,768 viewsStep-by-step explanation:
Given the relationship between the elapsed time, tea, in days since the videos first uploaded, and the total number of views, V(d) that the video received modeled by the following function
V(d)=\(4^{1.25d}\)
In order to know the number of views the video will receive after 6 days, we will substitute the number of days i.e d = 6 into the modeled equation as shown;
\(V(6)=4^{1.25(6)}\\V(6)=4^{7.5}\\V(6) = 32,768views\)
Answer:
32,768
Step-by-step explanation:
The equation y=4.2x could represent a variety of situations. Write your own description of a situation represented by this equation. Decide what quantities x and y represent in your situation.
Answers
Answer:
The solution is given below:
Step-by-step explanation:
Given that
The equation is 4.2x
It could present the total price for the no of goods
Here we take an example
The price per chips is $4.2
And, the number of chips purchased be x
And, the total price would be y
So if 5 chips were purchased, so the total price would be
y = $4.2 (5)
= $21
hence, the above represent the description
sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 1 ≤ r < 5, 3 4 ≤ ≤ 7 4
Answers
The region in the plane consists of points whose polar coordinates satisfy the given conditions, and it is enclosed by the circles r = 1 and r = 5, and the rays θ = 3π/4 and θ = 7π/4.
A more detailed explanation of the answer.
To sketch the region in the plane, follow these steps:
1. Identify the polar coordinate conditions: 1 ≤ r < 5, 3π/4 ≤ θ ≤ 7π/4.
2. Plot the radial boundaries: r = 1 and r = 5. These are circles with center at the origin (0, 0) and radii of 1 and 5, respectively.
3. Identify the angular boundaries: θ = 3π/4 and θ = 7π/4. These are rays extending from the origin at angles of 3π/4 (135°) and 7π/4 (315°), respectively.
4. Sketch the region enclosed by the radial and angular boundaries. The region will be a sector of an annulus (ring-like shape) bounded by the two circles and the two rays.
The region in the plane consists of points whose polar coordinates satisfy the given conditions, and it is enclosed by the circles r = 1 and r = 5, and the rays θ = 3π/4 and θ = 7π/4.
Learn more about polar coordinate.
brainly.com/question/11657509
#SPJ11
Which choice is equivalent to the expression below?
V-12
A. -24/5
B. 2123
C. -121
D. 231
E. 12 i
Answers
Given:
Consider the expression is \(\sqrt{-12}\).
To find:
The value of given expression.
Solution:
We have,
\(\sqrt{-12}\)
It can be written as
\(\sqrt{-12}=\sqrt{-1\times 12}\)
\(\sqrt{-12}=\sqrt{-1}\times \sqrt{12}\) \([\because \sqrt{ab}=\sqrt{a}\sqrt{b}]\)
\(\sqrt{-12}=i\times \sqrt{12}\) \([\because \sqrt{-1}=i]\)
\(\sqrt{-12}=\sqrt{12}i\)
Therefore, the value of given expression is \(\sqrt{12}i\).
Note: all options are incorrect.
find the value \((-1)x^{2}\)
Answers
the area of the shaded region is $78$ square inches. all angles are right angles and all measurements are given in inches. what is the perimeter of the non-shaded region?
Answers
The perimeter of the non-shaded region in the figure can be calculated to be 14 inches.
Given a figure.
The middle portion of the figure is not shaded.
It is required to find the perimeter of the non-shaded region.
It is given that:
The whole area of the shaded region = 78 inches²
The area of the small square which is situated at the bottom is:
Area of small square = 2 × 4
= 8 inches²
So, the area of the rest of the shaded area = 78 - 8
= 70 inches²
Now, the area of the whole region without the small square is:
Area = 10 × (10 - 2)
= 80 inches²
So, the area of the non-shaded region = 80 - 70
= 10 inches²
The width of the non-shaded rectangle is 2 inches.
So, length = 5 inches.
So, the perimeter is:
P = 2(5 + 2)
= 14 inches
Hence, the perimeter is 14 inches.
Learn more about Area and Perimeter here :
https://brainly.com/question/11957651
#SPJ12
The figure is given below.

The sampling distribution is based on the assumption that the _____ hypothesis is _____.
Answers
Answer:
NULL ; TRUE
Step-by-step explanation:
The sampling distribution is on the assumption that the null hypothesis is true .
The null hypothesis is a general statement that states that there
is no relationship between two phenomenon's under
consideration or that there is no association between two groups.
#SPJ4
Learn more about on
https://brainly.com/question/23056080
The sampling distribution is based on the assumption that the null hypothesis is TRUE.
A sampling distribution is a statistical probability distribution obtained from a large number of samples from a given population. In statistics, the population is the entire pool from which statistical samples are drawn. A population can refer to an entire group of people, things, events, visits, or measurements. A sampling distribution is the probability distribution of a statistic obtained by repeatedly sampling a specified population describes a set of possible outcomes for statistics, such as: B. Mean or mode of a population variable.A null hypothesis is a general statement that something is. There is no relationship between the two phenomena under or consider that there is no relationship between the two groups.
The sampling distribution is based on the assumption that the null hypothesis is TRUE.
Learn more about sampling distribution here
https://brainly.com/question/15713806
#SPJ4
Mr. Wright has 8 chicken pot pies to share among 6 people. If each person gets the same-size serving, how much chicken pot pie will each person get?
Answers
Explanation: if you divide how many pot pies/ how many people there are, you would get 8/6 which is equal to 1.33~
no clue how to do this, someone pls help

Answers
Answer:
6π
Step-by-step explanation:
First we need to find the circumference of the circle. We know that the radius is 4 and the formula is πd or 2πr
Leaving it in terms of pi, the circumference is 8π
Now we need to find the length of the arc.
Since the missing part of the circle is labeled with a right angle, we know that it's exactly 1/4 of the whole circle. That means the arc we need to find is 3/4 of the circumference.
3/4 of 8π is 6π
Elementary linear algebra (Inverse Linear Transformations) (Please explain in non-mathematical language as best you can)
C is a two-dimensional real vector space.
Define a linear transformation M : C →C via M(x) = ix. What is the matrix of this transformation for the basis {1,i}?
Answers
The matrix representation of M with respect to the basis {1, i} is:
[0 -1]
[1 0]
The linear transformation M takes complex numbers and multiplies them by the imaginary unit i. In this case, we want to represent this transformation using a matrix. To do that, we need to determine the images of the basis vectors 1 and i under M. For the basis vector 1, when we apply M to it, we get i as the result. Similarly, for the basis vector i, applying M gives us -1. These results form the columns of the matrix representation. Therefore, the matrix representing M with respect to the basis {1, i} is [0 -1; 1 0], where the first column corresponds to the image of 1 and the second column corresponds to the image of i.
For more information on linear transformation visit: brainly.com/question/29584270
#SPJ11
Two dice are cast. What is the probability that the sum of the two numbers does not exceed 10 (i.e. is less than or equal to 10)?
Answers
The probability is approximately 0.9167 or 91.67%.
To find the probability that the sum of two dice numbers does not exceed 10, we need to determine the favorable outcomes (sums less than or equal to 10) and the total possible outcomes when rolling two dice.
There are 36 possible outcomes when rolling two dice because each die has six faces (1, 2, 3, 4, 5, and 6), and the total number of outcomes is obtained by multiplying the number of outcomes for each die (6 * 6 = 36).
Now let's determine the favorable outcomes (sums less than or equal to 10):
When the sum is 2: There is only one combination (1 + 1).
When the sum is 3: There are two combinations (1 + 2 and 2 + 1).
When the sum is 4: There are three combinations (1 + 3, 2 + 2, and 3 + 1).
When the sum is 5: There are four combinations (1 + 4, 2 + 3, 3 + 2, and 4 + 1).
When the sum is 6: There are five combinations (1 + 5, 2 + 4, 3 + 3, 4 + 2, and 5 + 1).
When the sum is 7: There are six combinations (1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, and 6 + 1).
When the sum is 8: There are five combinations (2 + 6, 3 + 5, 4 + 4, 5 + 3, and 6 + 2).
When the sum is 9: There are four combinations (3 + 6, 4 + 5, 5 + 4, and 6 + 3).
When the sum is 10: There are three combinations (4 + 6, 5 + 5, and 6 + 4).
Adding up the favorable outcomes, we get: 1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 = 33.
Therefore, the probability that the sum of the two dice numbers does not exceed 10 is given by:
Probability = Favorable outcomes / Total outcomes = 33 / 36 = 11/12 ≈ 0.9167.
So, the probability is approximately 0.9167 or 91.67%.
Learn more about probability from
https://brainly.com/question/30390037
#SPJ11
the time between calls to a plumbing supply business is exponentially distributed with a mean time between calls of 16 minutes. (a) what is the probability that there are no calls within a 30-minute interval? (round your answer to 4 decimal places.) (b) what is the probability that at least one call arrives within a 10-minute interval? (round your answer to 4 decimal places.) (c) what is the probability that the first call arrives within 5 and 10 minutes after opening? (round your answer to 4 decimal places.) (d) determine the length of an interval of time such that the probability of at least one call in the interval is 0.90. minutes (round your answer to 2 decimal places.)
Answers
(a) The probability that there are no calls within a 30-minute interval is approximately 0.3680. (b) 0.4689. (c) 0.2160. (d)47.60 minutes.
(a) To find the probability that there are no calls within a 30-minute interval, we can use the exponential distribution. The parameter λ (lambda) for the exponential distribution is equal to 1/mean.
Given that the mean time between calls is 16 minutes, we can calculate λ as:
λ = 1/16
Now, let's calculate the probability using the exponential distribution formula:
P(no calls within 30 minutes) = e^(-λt)
P(no calls within 30 minutes) = e^(-(1/16) * 30)
P(no calls within 30 minutes) ≈ 0.3680
So, the probability that there are no calls within a 30-minute interval is approximately 0.3680.
(b) To find the probability that at least one call arrives within a 10-minute interval, we can use the complementary probability. The complementary probability is 1 minus the probability of no calls within the interval.
P(at least one call within 10 minutes) = 1 - P(no calls within 10 minutes)
P(at least one call within 10 minutes) = 1 - e^(-λt)
P(at least one call within 10 minutes) = 1 - e^(-(1/16) * 10)
P(at least one call within 10 minutes) ≈ 0.4689
So, the probability that at least one call arrives within a 10-minute interval is approximately 0.4689.
(c) To find the probability that the first call arrives within 5 and 10 minutes after opening, we can subtract the probability of no calls within 10 minutes from the probability of no calls within 5 minutes.
P(first call within 5-10 minutes) = P(no calls within 10 minutes) - P(no calls within 5 minutes)
P(first call within 5-10 minutes) = e^(-λ*10) - e^(-λ*5)
P(first call within 5-10 minutes) ≈ 0.2160
So, the probability that the first call arrives within 5 and 10 minutes after opening is approximately 0.2160.
(d) To determine the length of an interval of time such that the probability of at least one call in the interval is 0.90, we need to find the value of t that satisfies the equation:
P(at least one call within t minutes) = 0.90
Using the exponential distribution formula:
1 - e^(-λt) = 0.90
e^(-λt) = 1 - 0.90
e^(-λt) = 0.10
Taking the natural logarithm of both sides:
-λt = ln(0.10)
t = ln(0.10) / -λ
Substituting λ = 1/16:
t ≈ 47.5957 minutes
So, the length of the interval of time such that the probability of at least one call is 0.90 is approximately 47.60 minutes.
To learn more about probability visit:
brainly.com/question/14289833
#SPJ11
Find the value of x in the triangle shown below

Answers
Answer:
A) x=sq rt 80
Step-by-step explanation:
by the Pythagorean theorem
4^2+8^2=x^2
16+64=x^2
80=x^2
x=sq root 80
Answer:
Step-by-step explanation:
Pythagorean theorem,
Hypotenuse² = Altitude² + Base²
x² = 8² + 4²
= 64 + 16
= 80
x = √80
Can someone help me with this please!

Answers
Answer:
The answer is C.
mark me brainliest!
find out the slope n y intercept.
What is the nth term of the sequence below?
2, 6, 12, 20, . . .
A. \(n {}^{2} \: + \: 1\)
B. \(3n\)
C. \(n(n \: + \: 1)\)
D. \( {n}^{2} \: - \: 1\)
Answers
Answer:
Option C
Kindly award branliest
Step-by-step explanation:
Tn = n(n + 1)
T1 = 1(1 +1) = 1(2) = 2
T2 = 2(2+1) = 2(3) =6
T3 = 3(3 + 1) = 3(4) = 12
T4 = 4(4 + 1) = 4(5) = 20
... It obeys
Make x the subject of m= n + x/p
Answers
Answer:
x = m × p - n
Step-by-step explanation:
\(m = n + \frac{x}{p} \)
We can first multiply both sides by p.
\(m \times p = n + x\)
And now we only have n left with x, so we subtract n on both sides.
\(m \times p - n = x \\or \\ x = m \times p - n\)
It is known that X has a uniform distribution with μ=0.5 minutes and σ=0.29 minutes. Suppose a random sample of 64 people is selected. The shape of the sampling distribution of X
ˉ is: Uniform Approximately Normal Normal not enough information to determine
Answers
In this scenario, the shape of the sampling distribution of X-bar is approximately normal.
The sampling distribution of the sample mean, X-bar, can be determined by the Central Limit Theorem. In this case, since the sample size is large (n = 64) and the underlying distribution (X) is approximately normal, the sampling distribution of X-bar will also be approximately normal. The Central Limit Theorem states that regardless of the shape of the population distribution, as the sample size increases, the sampling distribution of X-bar tends to become more and more normal. Therefore, in this scenario, the shape of the sampling distribution of X-bar is approximately normal.
For more information on uniform distribution visit: brainly.com/question/15301850
#SPJ11
Tracey and Mark recorded the number of customers waiting in the first 5 checkout lines at two different grocery stores at the same time of day on the same day of the week. Tracey found {2, 2, 3, 3, and 4} waiting customers in store A. In store B, Mark found {3, 4, 4, 4, and 5} waiting customers. Which one of the following statements is true?
Store A has a spread of 2. 8.
Store A has a spread of 2. 8.
Stores A and B have an equal spread.
Stores A and B have an equal spread.
Store B has a greater spread than store A.
Store B has a greater spread than store A.
Store B has a spread of 4
Answers
The correct statement is "Stores A and B have an equal spread." (option b).
To determine the spread of the data, we first need to find the range. The range is calculated by subtracting the smallest number from the largest number in a dataset.
For Store A:
The smallest number recorded is 2, and the largest number is 4. Therefore, the range of Store A is 4 - 2 = 2.
For Store B:
The smallest number recorded is 3, and the largest number is 5. Thus, the range of Store B is 5 - 3 = 2.
Comparing the ranges of both stores, we see that both Store A and Store B have the same range, which means the spread of the data is equal for both stores.
Therefore, the correct statement is:
b) Stores A and B have an equal spread.
To know more about range here
https://brainly.com/question/17440903
#SPJ4
Please help I really dont know where to start and am having a hard time with this unit

Answers
So a slope of 1/4 means that for every 4 steps you take forward, you would go up 1.
With this, beginning at the point (6,3), lets take 4 steps back and go down 1. This is instead of going forward, as that value would be outside of your graph We would end up at (2,2). By using these two points, you can graph your line.

solve for x in [0, π]: 2 cos(x) > sec(x)
Answers
The value for x is 7π/6 and 11π/6.
sin2xsecx+2cosx=0
(2sinxcosx)(1/cosx)+2cosx=0
sinxcosx/cosx+2cosx=0
So,
2sinx+2cosx=0
2(sinx+cosx)=0
(2(sinx+cosx))²=0
4(sin²x+cos²x+2sinxcosx)=0
hence,
(sin²x+cos²x+2sinxcosx)/4=0/4
sin2x+cos2x+2sinxcosx=0
1+sin2x=0
sinx=−1/2
=7π/6 and 11π/6
Know more about trigonometry at:
https://brainly.com/question/20519838
#SPJ4
by how much does -12 exceed -15
Answers
Answer:
By 3.
Step-by-step explanation:
-12-3=-15
Hope this helps!
Answer:
-12 exceeds -15 by 3
Step-by-step explanation:
To find out by how much a exceeds b, subtract a - b.
For example, by how much does 8 exceed 6?
Here, a = 8 and b = 6.
a - b = 8 - 6 = 2
2 is correct since we know that 8 is 2 greater than 6.
Now we do this problem.
By how much does -12 exceed -15?
a = -12; b = -15
a - b = -12 - (-15) = -12 + 15 = 3
Answer: -12 exceeds -15 by 3
5. Given AADL AAKM with AD = 14, DK = 21, and
AL= 15. What is the measure of LM?

Answers
Answer:
22.5
Step-by-step explanation:
first of all, the first sign in the designations of the triangles is not an A. it is the Greek Delta (capital) sign. standing for "triangle" due to its shape.
as the diagram shows (and the description says correctly), ADL and AKM are similar triangles.
that means they have the same angles.
and in order to keep the same angles even when the lengths of the sides are different, the relative relation of the side lengths must be the same for all sides.
that means, if one side changes by a factor f, then both other sides must change by the same factor.
so, by checking the change factor for AD (to AK), we can then determine the change of AL to AM. and then we simply subtract AL from AM and get LM.
the original AD = 14.
AK = AD + DK = 14 + 21 = 35
the change factor f is then AK/AD = 35/14 = 5/2
in other words AD grew by a factor of 5/2.
AM is then created by applying the same factor to AL.
=> AM = 15 * 5 / 2 = 75 / 2 = 37.5
=> LM = AM - AL = 37.5 - 15 = 22.5
Step-by-step explanation:
intindihin nyo na lang.

A plane flying with a constant speed of 25 km/min passes over a ground radar station at an altitude of 12 km and climbs at an angle of 30 degrees. At what rate, in km/min is the distance from the plane to the radar station increasing 2 minutes later?
Your answer: ____ kilometers per minute.
Hint: The law of cosines for a triangle is c²=a²+ b²-2ab cos (theta)
where theta is the angle between the sides of length a and b.
Answers
the distance from the plane to the radar station is increasing at a rate of approximately 30.84 kilometers per minute.
What is the right-angle triangle?A triangle is said to be right-angled if one of its angles is exactly 90 degrees. The total of the other two angles is 90 degrees. Perpendicular and the triangle's base are the sides that make up the right angle. The longest of the three sides, the third side is known as the hypotenuse.
Given, A plane flying with a constant speed of 25 km/min passes over a ground radar station at an altitude of 12 km and climbs at an angle of 30 degrees.
We can use the law of cosines to find d:
d² = 12² + (h + 12)² - 2(12)(h + 12)cos(θ)
Since the plane is climbing at an angle of 30 degrees, we can use trigonometry to find h:
sin(30) = h / (25 km/min * 2 min)
h = 25 km/min
Now we can substitute this value of h into the equation for d and simplify:
d² = 12² + (25 + 12)² - 2(12)(25 + 12)cos(θ)
d² = 12² + 37² - 2(12)(37)cos(θ)
d² = 144 + 1369 - 888cos(θ)
d² = 1513 - 888cos(θ)
To find the rate at which d is changing, we can take the derivative of both sides of this equation with respect to time:
2dd/dt = -888(d(cos(θ))/dt)
Since the plane is flying with a constant speed of 25 km/min, we can use trigonometry to find d(cos(θ))/dt:
cos(θ) = 12/d
d(cos(θ))/dt = -(12/d²)(dd/dt)
d(cos(θ))/dt = -(12/d²)(25 km/min)
Now we can substitute these values into the equation for the rate of change of d:
2dd/dt = -888(-(12/d²)(25 km/min))
2dd/dt = (888*12)/(d²)(25 km/min)
dd/dt = (5328)/(d²) km/min
Finally, we can substitute the value we found for d into this equation to get the rate at which d is changing 2 minutes later:
d = sqrt(1513 - 888cos(θ))
θ = 30 degrees
dd/dt = (5328)/(d²) km/min
dd/dt = (5328)/(1513 - 888cos(30)) km/min
dd/dt ≈ 30.84 km/min
Therefore, the distance from the plane to the radar station is increasing at a rate of approximately 30.84 kilometers per minute.
Learn more about right-angle triangles here:
https://brainly.com/question/3770177
#SPJ1

PLEASE HELP ME I CANT FAIL I WILL GIVE YOU SO MUCH POINTS IF YOU HELP! What is the product of -2 2/5 and -3 5/6?
A- -9 1/5
B- -6 7/30
C- 6 1/3
D- 9 1/5

Answers
Answer:
The answer is 9 1/5.Step-by-step explanation:
Step-1: Convert the mixed fractions into improper fractions.
=> -2 2/5 ⇒ -12/5=> -3 5/6 ⇒ -23/6Step-2: Multiply the improper fractions.
=> -12/5 x -23/6=> 12/5 x 23/6[The minuses on both fractions cancelled out because when there are 2 minuses multiplying each other, the minuses cancel out.]
=> 2/5 x 23/1=> 46/5Step-3: Convert the improper fraction into mixed fraction.
=> 46/5 = 9 1/5Hence, the answer is 9 1/5.
Hoped this helped.
\(BrainiacUser1357\)
Is 82 inches grater than 5feet and 10 inches
Answers
Answer:
False, 82 inches is not greater than 5 feet and 10 inches
Step-by-step explanation:
1 feet = 12 inches
5x12=60+10=70
82 is greater than 70.
When Kiran runs the 400 meter dash, his finishing times are normally
distributed with a mean of 65 seconds and a standard deviation of 0.5
seconds. Using the empirical rule, what percentage of races will his finishing
time be between 64.5 and 65.5 seconds?
Answers
The percentage of races in will his finishing time is between 64.5 and 65.5 seconds is 68%.
What is an empirical rule?According to the empirical rule, also known as the 68-95-99.7 rule, the percentage of values that lie within an interval with 68%, 95%, and 99.7% the values lies within one, two, or three standard deviations of the mean of the distribution.
\(\rm P(\mu - \sigma \ \ < X < \mu + \sigma) \ \approx 68\%\\\\P(\mu - 2\sigma < X < \mu + 2\sigma) \approx 95\%\\\\P(\mu - 3\sigma < X < \mu + 3\sigma) \approx 99.7\%\)
where we had were mean of the distribution of X is μ and the standard deviation from the mean of the distribution of X is σ (assuming X is normally distributed).
When Kiran runs the 400 meters dash, his finishing times are normally distributed with a mean of 65 seconds and a standard deviation of 0.5 seconds.
Then by the formula, we have
\(\rm P (65-0.5 < X < 65+0.5) = P(64.5 < X < 65.5) \approx 68\%\)
Learn more about the empirical rule here:
https://brainly.com/question/13676793
#SPJ2
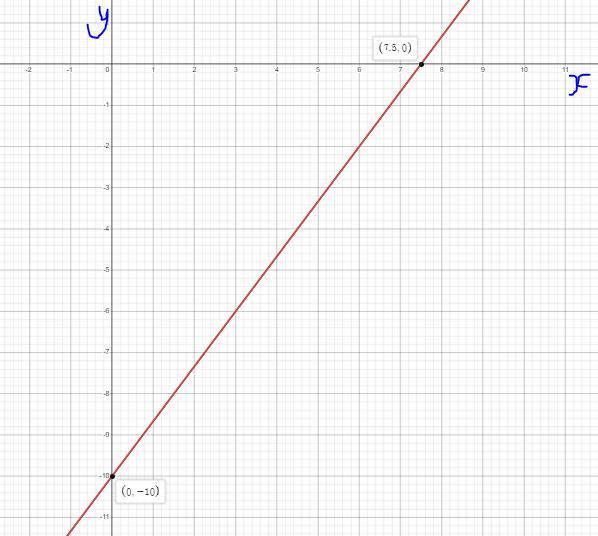
-4x+3y=-30
Use intercepts to graph the linear equation.
x-intercept?
y-intercept?
Answers
The graph of -4x+3y=-30 is shown below.
The x-intercept of -4x+3y=-30 is: 7.5
The y-intercept of -4x+3y=-30 is: -10.
What are the x and y-intercepts of a Linear Equation?The x-intercept of a linear equation can be determined from its graph, where it is the point where the x-axis it intercepted by the line.
On the other hand, the y-intercept is the point on the y-axis that the graph intercepts or crosses.
Given the linear equation, -4x+3y=-30, find the x and y-intercepts as shown below:
Find the x-intercept by substituting y = 0 into -4x+3y=-30:
-4x + 3(0) = -30
-4x = -30
x = -30/-4
x = 7.5
x-intercept is 7.5
Find the y-intercept by substituting x = 0 into -4x + 3y = -30:
-4(0) + 3y = -30
3y = -30
y = -30/3
y = -10.
y-intercept is -10.
The graph of the linear equation that shows the x and y-intercepts is shown in the diagram below.
Learn more about x and y-intercepts on:
https://brainly.com/question/8058870
#SPJ1
Take the first 4 digits of your student number as the first number and the last 3 digits as the second number. Write the matlab code to find the greatest common divisor of these numbers using the Euclidean algorithm.
Answers
The required Matlab code to find the greatest common divisor of a number using the Euclidean algorithm is shown.
To find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm in MATLAB, you can use the following code:
% Replace '12345678' with your actual student number
studentNumber = '12345678';
% Extract the first 4 digits as the first number
firstNumber = str2double(studentNumber(1:4));
% Extract the last 3 digits as the second number
secondNumber = str2double(studentNumber(end-2:end));
% Find the GCD using the Euclidean algorithm
gcdValue = gcd(firstNumber, secondNumber);
% Display the result
disp(['The GCD of ' num2str(firstNumber) ' and ' num2str(secondNumber) ' is ' num2str(gcdValue) '.']);
Make sure to replace '12345678' with your actual student number. The code extracts the first 4 digits as the first number and the last 3 digits as the second number using string indexing. Then, the gcd function in MATLAB is used to calculate the GCD of the two numbers. Finally, the result is displayed using the disp function.
Learn more about Matlab code here:
https://brainly.com/question/30763780
#SPJ4
I need help please!

Answers
Answer:
Tell me you address right now!!!
Step-by-step explanation:
I am gonna call police for help!
➤ Solve the inequalities.
T -3 is less than or equal to 2
Answers
-3 is less than 2
< is the symbol