100 POINTS WILL AWARD BRAINLIEST
complete the two column proof, images are below

Answer:

%50

Step-by-step explanation:

hope this helped luv!

The absolute value of the sum of two integers does not exceed the sum of the absolute values ​​of these integers. ∀x, ∀y, |x + y|≤|x| + |y| .

What is inequality?

An inequality in mathematics depicts the connection between two values in an algebraic statement that are not equal. One of the two variables on the two sides of the inequality may be greater than, greater than or equal to, less than, or less than or equal to another value, according to inequality signals.

The absolute value of the sum of two integers does not exceed the sum of the absolute values ​​of these integers. ∀x, ∀y, |x + y|≤|x| + |y| .

This inequality, sometimes called as the triangle inequality.

To learn more about the inequality from the given link

https://brainly.com/question/25275758

#SPJ4

The absolute value of the sum of two integers does not exceed the sum of the absolute values ​​of these integers. ∀x, ∀y, |x + y|≤|x| + |y| .

What is inequality?

An inequality in mathematics depicts the connection between two values in an algebraic statement that are not equal. One of the two variables on the two sides of the inequality may be greater than, greater than or equal to, less than, or less than or equal to another value, according to inequality signals.

The absolute value of the sum of two integers does not exceed the sum of the absolute values ​​of these integers. ∀x, ∀y, |x + y|≤|x| + |y| .

This inequality, sometimes called as the triangle inequality.

To learn more about the inequality from the given link

brainly.com/question/25275758

#SPJ4

Answer:

921.05

Step-by-step explanation:

Answer:

921.05

Step-by-step explanation:

If 19% of a number is 175, then what is 100% of that number? Setup the equation.

Solve for Y

Using cross multiplication of two fractions, we get

19Y = 175 x 100

19Y = 17500

Y = 17500

100 = 921.05

Answer:

2((3(4) + 4(7) + 3(7)) = 2(12 + 28 + 21) = 2(61) = 122 square meters

BDEO Sixteen is equivalent to 48408 in base ten.

What is the equivalent expression?

Equivalent expressions are expressions that perform the same function despite their appearance. If two algebraic expressions are equivalent, they have the same value when we use the same variable value.

To convert BDEO Sixteen to base ten, we need to first expand the value of each digit in the number using the powers of 16.

BDEO Sixteen = (11 x 16³) + (13 x 16²) + (14 x 16¹) + (0 x 16⁰)

Simplifying this expression, we get:

BDEO Sixteen = (11 x 4096) + (13 x 256) + (14 x 16) + (0 x 1)

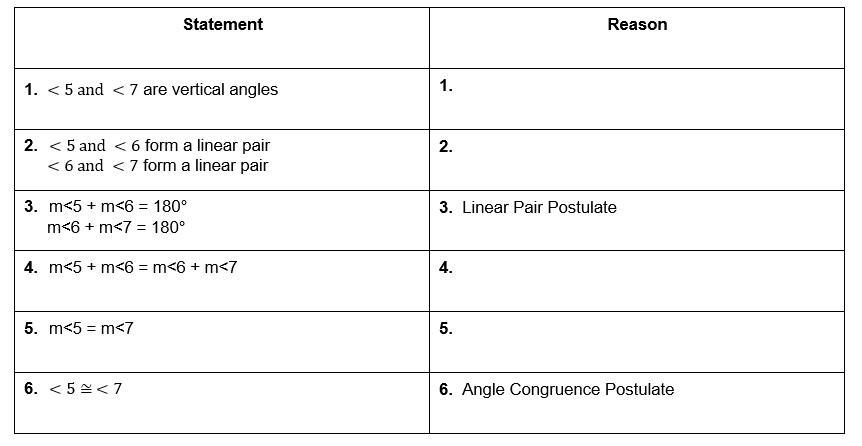
BDEO Sixteen = 45056 + 3328 + 224 + 0

BDEO Sixteen = 48408

Therefore, BDEO Sixteen is equivalent to 48408 in base ten.

To learn more about the equivalent expression visit:

https://brainly.com/question/2972832

#SPJ1

Answer:

B

Step-by-step explanation:

Because -15 + 2 = -13

The data in the table can be modeled by this linear equation in slope-intercept form: y = 8x - 5.

The slope is 8, which means the wages earned increases at rate of 8 dollars per hour as the time increases.

The y-intercept is -5 and it represent the initial wages earned.

In Mathematics and Geometry, the slope-intercept form of the equation of a straight line is represented by this mathematical expression;

y = mx + c

Where:

First of all, we would determine the slope of this line;

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

Slope (m) = (24.00 - 8.00)/(3 - 1)

Slope (m) = 16.00/2

Slope (m) = 8

At data point (1, 3), a linear equation in slope-intercept form for this line can be calculated as follows:

y - y₁ = m(x - x₁)

y - 3 = 8(x - 1)

y = 8x - 8 + 3

y = 8x - 5

Read more on slope here: https://brainly.com/question/20282417

#SPJ1

Answer:

30 hot dogs fewer.

Answer:

For acute angles, remember what sine means: opposite over hypotenuse. If we increase the angle, then the opposite side gets larger. That means "opposite/hypotenuse" gets larger or increases.

Step by Step:

Keep this in mind >>

Consider the unit circle > The sine and cosine ratios are the only ratios that have 1 (the radius or hypotenuse) as the denominator. The numerators (sides) vary between 0 and 1, thus determining that the sine and cosine do the same.

All of the other ratios (tangent, cotangent, secant, cosecant) have a side as the denominator, varying between 0 and 1. As any denominator approaches 0, the value of the ratio approaches infinity.

The temperature at the bottom of the mountain is 50.9 °C.

Let's work through the given information step by step to find the temperature at the bottom of the mountain.

The temperature in the hotel is 21 °C.

The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.

Let's denote the temperature at the top of the mountain as T_top.

So, the temperature in the hotel can be expressed as T_top + 26.7 °C.

The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.

Let's denote the temperature at the bottom of the mountain as T_bottom.

So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.

Now, let's combine the information we have:

T_top + 26.7 °C = T_bottom - 3.2 °C

To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:

T_bottom = T_top + 26.7 °C + 3.2 °C

T_bottom = T_top + 29.9 °C

Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:

T_bottom = 21 °C + 29.9 °C

T_bottom = 50.9 °C

Therefore, the temperature at the bottom of the mountain is 50.9 °C.

for such more question on temperature

https://brainly.com/question/14820864

#SPJ8

Answer:

The equation of this line is y = -4.

Answer:

y=-4

Step-by-step explanation:

zero slope m=0

y-y1=m(x-x1)

y-(-4)=0(x-(-9))

y+4=0

y=-4

The algebraic property illustrated is the commutative property of multiplication

The properties of algebra are those properties mostly used in simplifying algebraic expressions.

Algebraic properties are:

From the expression given we have

4/5 • 5/4 = 1

= 4/ 5 × 5/ 4

= 1

Thus, the algebraic property illustrated is the commutative property of multiplication

Learn more about algebraic property here:

https://brainly.com/question/855307

#SPJ1

a. The areas of the square is 81m² and for rectangle is 72m²

b. The perimeter of the square is 40m

a. To determine the area of the shapes in which we have that have a perimeter of 36m, we can consider rectangle and square.

For a square;

Perimeter of square = 4L

36 = 4L

L = 9m

The area of the square will be L² = 9² = 81m²

For a rectangle;

The perimeter of rectangle is;

P = 2(L + W)

We can assume that two numbers which will represent the length and width are;

L = 12m, W = 6m or L = 6m, W = 12m

A = 12 * 6 = 72m²

b.

The area of the wire is 100m², the perimeter for this can be calculated when we consider square and rectangle;

Perimeter of square = 4L

Area of square = L² = 100m²

L = 10m

The perimeter of the wire is 4(10) = 40m

Learn more on perimeter and area of rectangle and square here;

https://brainly.com/question/25292087

#SPJ1

The Vertex is : (-6, -30)

The X-intercepts are : Approximately (-10.89, 0) and (-1.11, 0)

The Y-intercept is : (0, 6)

The Axis of symmetry is : x = -6

The functions Domain: is All real numbers

The Range is : All real numbers greater than or equal to -30.

To sketch the graph of the quadratic function \(f(x) = x^2 + 12x + 6,\) we can start by identifying the vertex, x-intercepts, y-intercept, axis of symmetry, domain, and range.

To find the vertex, we can use the formula x = -b/2a, where a, b, and c are the coefficients of the quadratic equation in standard form\((ax^2 + bx + c).\)

In this case, a = 1, b = 12, and c = 6.

Applying the formula, we get x = -12/(2 \(\times\) 1) = -6.

To find the y-coordinate of the vertex, we substitute this x-value into the equation:\(f(-6) = (-6)^2 + 12(-6) + 6 = 36 - 72 + 6 = -30.\)

So, the vertex is (-6, -30).

To determine the x-intercepts, we set f(x) = 0 and solve for x. In this case, we need to solve the quadratic equation \(x^2 + 12x + 6 = 0.\)

Using factoring, completing the square, or the quadratic formula, we find that the solutions are not rational.

Let's approximate them using decimal values: x ≈ -10.89 and x ≈ -1.11. Therefore, the x-intercepts are approximately (-10.89, 0) and (-1.11, 0).

The y-intercept is obtained by substituting x = 0 into the equation: \(f(0) = 0^2 + 12(0) + 6 = 6.\)

Thus, the y-intercept is (0, 6).

The axis of symmetry is the vertical line that passes through the vertex. In this case, it is the line x = -6.

The domain of the function is all real numbers since there are no restrictions on the possible input values of x.

To determine the range, we can observe that the coefficient of the \(x^2\) term is positive (1), indicating that the parabola opens upward.

Therefore, the minimum point of the parabola occurs at the vertex, (-6, -30).

As a result, the range of the function is all real numbers greater than or equal to -30.

For similar question on Vertex.

https://brainly.com/question/25651698

#SPJ8

Answer:

–2x – 2

Step-by-step explanation:

-2 (x - 1) + -4

= -2x - (-2) + -4

THINGS TO KNOW

– × – = +

+ × + = +

– × + = –

+ × – = –

–2x + 2 –4

–2x – 2

The final answer is : –2x – 2

Answer:

To determine the amount of engine oil needed, we need to find 5% of 3.8 gallons:

0.05 x 3.8 = 0.19

So, 0.19 gallons of engine oil should be added to the jerry can.

288 ounces of water are left in the water tank.

What is arithmetic?

Arithmetic is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers—addition, subtraction, multiplication, division, exponentiation, and extraction of roots

Here, we have

Given: Tom has a water tank that holds 5 gallons of water. tell me this is water for my footing to fill six bottles they each hold 16 ounces and a picture that holds one over 2 gallons.

1 gallon = 128 ounces, 2 gallon = 256 ounces

6 bottles × 16 ounces = 96 ounces

2 gallon + 96 ounces = 256 + 96 ounces = 352 ounces

5 gallon = 5 × 128 = 640 ounces

= 640 - 352 = 288 ounces

Hence,  288 ounces of water are left in the water tank.

To learn more about the arithmetic from the given link

https://brainly.com/question/28369191

#SPJ1

To solve the question, we will apply the principle

If the sides are not equal, the sum of the two shortest sides must be greater than the longest sides

For option A

3 cm, 3cm, 3cm

All sides are equal so it satisfies the condition for a triangle

For option B

The sum of the two shorter sides (4cm and 8cm) = 12cm

while the longest side is 12cm

Since the sum of 12cm is not more than the longest side, then

the sides are NOT suitable for a triangle

For option C

5cm + 9cm = 14 cm

The longest side = 14cm

Since the sum 14cm is not greater than the longest side, then

the sides are NOT suitable for a triangle

For option D

Sum of the shorter sides = 6cm + 7cm = 13cm

longest side = 8cm

Since the sum of 13cm is greater than 8cm, then it is suitable for a triangle

For option E

Sum of shorter sides = 7cm + 7cm = 14cm

longer side = 10cm

Since the sum of 14cm is greater than 10cm, then it is suitable for a triangle

Answer:

I have completed the answers and attached them to the explanation.

Step-by-step explanation:

Answer:

Step-by-step explanation:

The question asks for a subtraction expression:

length is always a positive number so bigger number first here.

OB = 4-(-1)              >only moves in x direction so subtract x's

AB = 4-(-2)             >only moves in y direction so subtract y's

Answer:

15833.6269741 cm^3.But we can make it 15,833.63 cm^3 rounded to the nearest hundredth.

Step-by-step explanation:

so let’s solve this using the following formula -> \(V=\pi r^2h\).

So if the height is 25 and the radius is 12 them we can plug those numbers into the formula.

\(\pi (12)^2(35)\).

So let’s start by doing 12 squared which is 144 then 144*35 which is 5040.

And now 5040*pi which is 15833.6269741 cm^3.But we can make it 15,833.63 cm^3 rounded to the nearest hundredth.

Id you ant to check if my answer is correct look at the image below.

Answer:

The medal received by an Olympic gymnast has a nominal level of measurement.

Step-by-step explanation:

The variable, X can be described as the type of medal received by an Olympic gymnast.

The values that X can take are: gold, silver and bronze.

The variable X is a qualitative variable, since it describes the different categories of winning a medal.

There are two types of qualitative variable level of measurement:

In case of nominal level of measurement, words, letters, and alpha-numeric symbols are used to denote the category.  For instance, the data about individuals belonging to three different gender categories, the data about individual’s different eye color.

Thus, the medal received by an Olympic gymnast has a nominal level of measurement.

1)Test Static: 1.82

2)P-Value: < 0.05

3)Decision: i. Reject the null hypothesis.

To test the claim that the population mean is greater than 90, we can use a one-sample t-test.

(a) The test statistic for the one-sample t-test is calculated as:

Plugging in the values, we get:

(b) To find the p-value for the test, we can use a t-table or a statistical software package to find the probability of observing a t-value as extreme or more extreme than the one we obtained, given that the null hypothesis is true. For a one-tailed test with α = 0.05 and df = 99 (the sample size - 1), the critical value for t is approximately 1.65. Since our test statistic (1.82) is greater than the critical value, the p-value is less than 0.05.

(c) Since the p-value is less than the significance level of α = 0.05, we reject the null hypothesis and conclude that the population mean is indeed greater than 90. Therefore, the decision for this test is: i. Reject the null hypothesis.

Learn more about one-sample t-test here:

https://brainly.com/question/26717173

#SPJ4

All the areas of the circles are illustrated below.

The circumference of a circle is the distance around the circle which is 2πr.

The diameter of a circle is the largest chord that passes through the center of a circle it is 2r.

We know, The area of the circle is πr².

1. The area of the circle with a radius of 2.5 cm is,

= π(2.5)² sq cm.

= 19.625 sq cm.

2. The area of the circle with a radius of 11 in is,

= π(11)² sq in.

= 379.94 sq in.

3. The area of the circle with a radius of 3 mm is,

= π(3)² sq mm.

= 28.26 sq mm.

4. The area of the circle with a radius of 5 in is,

=  π(5)² sq in.

= 78.5 sq in.

5.  The area of the circle with a radius of 6.5 cm is,

= π(6.5)² sq cm.

= 132.665 sq cm.

6.   The area of the circle with a radius of 7.2 yd is,

= π(7.2)² sq yd.

= 162.7776 sq yd.

learn more about circles here :

https://brainly.com/question/29142813

#SPJ1

The total centimeters that the plants grew in all was 200 centimeters or 2.00 centimeters when written as a decimal.

Centimetres (cm) is a unit of length in the metric system, equal to one-hundredth of a metre. It is commonly used in everyday life, for example when measuring the height of a person or the size of a room. Centimetres are also used in scientific and engineering measurements, such as the size of an object or the distance between two points. Centimetres are divided into millimetres, which are one-thousandth of a metre.

This can be written as a decimal as 2.00 centimeters.

To determine the total centimeters, we simply add the individual centimeter measurements of the two plants.

Daysha's plant grew 100 centimeters and India's plant grew 100 centimeters.

Therefore, the total centimeters that the plants grew in all was 200 centimeters, or 2.00 centimeters when written as a decimal.

To know more about distance click-

http://brainly.com/question/23848540
#SPJ1

Given that:

- The sample size is 28 city residents:

- The mean of the time (in years) they had lived at their present address was:

- The standard deviation (in years) of the population was:

Then, you need to use the following formula for calculating the Confidence Interval given the Mean:

Where μ is the sample mean, σ is the standard deviation, "z" is the z-score, and "n" is the sample size.

By definition, the z-score for a 90% confidence interval is:

Therefore, you can substitute values into the formula and evaluate:

You get that the lowest value is:

And the highest value is:

Hence, the answer is:

Answer:

x = 16°

Step-by-step explanation:

What we know:

∠JML = 47°

∠JKL = (7x + 21)°

∠JML is an inscribed angle

∠JKL is an inscribed angle

Inscribed angles are half of the value of their intercepted arc

So if m∠JML = 47° then mArc JL is double that or 94°

And ∠JKL is intercepted by Arc JML which is the rest of the circle not intercepted by ∠JML so

mArc JL + Arc JML = 360°

94 + Arc JML = 360

Subtract 94 from both sides to isolate Arc JML

Arc JML = 266°

So if Arc JML = 266° then it's intercepted inscribed angle is half of that.

Arc JML ÷ 2 = ∠JKL

266 ÷ 2 = ∠JKL

133 °= ∠JKL

Now we can use this value and set it equal to the expression to find the value of x

(7x + 21) = 133

Subtract 21 from both sides to isolate the x

7x = 112

Divide both sides by 7

x = 16

Answer:

c

Step-by-step explanation:

Step-by-step explanation:

\( \frac{12 \times 3}{23 \times 3} = \frac{36}{69} \)