11. Phyllis ran in a 5-kilometer race to help raise money for the school. How many meters long is the race?
Answers
Answer:5000 meters
Step-by-step explanation:1km=1000m
Related Questions
X+Y=17 and XY=164 find the vale of X and Y
Answers
There are no real values for X and Y that satisfy the given equations X + Y = 17 and XY = 164.
To find the values of X and Y in the given equations, we can use a system of equations approach.
Let's start by solving the first equation, X + Y = 17, for one variable in terms of the other. We can choose to solve for X:
X = 17 - Y
Now, substitute this expression for X in the second equation, XY = 164:
(17 - Y)Y = 164
Expanding the equation gives us:
17Y - Y^2 = 164
Rearranging the equation to a quadratic form, we have:
Y^2 - 17Y + 164 = 0
To solve this quadratic equation, we can use factoring, completing the square, or the quadratic formula. Let's use the quadratic formula:
Y = (-(-17) ± √((-17)^2 - 4(1)(164))) / (2(1))
Simplifying further:
Y = (17 ± √(289 - 656)) / 2
Y = (17 ± √(-367)) / 2
Since the expression under the square root is negative, there are no real solutions for Y. This means that there are no real values for X and Y that satisfy both equations simultaneously.
for such more question on values
https://brainly.com/question/11546044
#SPJ8
Tick the calculations that would increase 275 by 10%.
A 275 + 10
B
110
x 275
100
С
10
x 275
100
D 275 + 27.5
Answers
Answer:
D & B
Step-by-step explanation:
The triangles are similar, find the length of the unknown side. Round your answers to the nearest tenth (0.1), if necessary.
please help me

Answers
Answer:
\(22\)
Step-by-step explanation:
Similar shapes must have corresponding sides in a constant proportion. Therefore, we can set up the following equation and solve for \(?\):
\(\frac{28}{42}=\frac{?}{33}\) (divide corresponding sides)
\(\frac{28}{42}=\frac{?}{33},\\\\?=\frac{28\cdot 33}{42}=\boxed{22}\)
Describe some advantages and some disadvantages of a recursive formula and an explicit formula. When is it appropriate to use each formula?
Answers
The explicit formula has the benefit of making it simple to locate any term in the sequence. The recursive formula only includes one addition or multiplication operation, hence this formula's drawback is that it has more operations overall.
What is recursive formula?We discovered that a recursive rule is a rule that repeatedly alters a prior number in order to reach a subsequent number. As an illustration, our formula for counting numbers is recursive since each number is equal to the preceding number plus 1.
A recursive function is one that generates a series of phrases by repeating or using its own prior term as input.
To learn more about recursive formula from the given link:
brainly.com/question/8972906
#SPJ4
Let f be the function defined by f(x) For how many values of x in the open interval (0, 1.565) is the instantaneous rate of change of f equal to the average rale of change = of f on the closed interval [0. 1.565] (A) Zero (B) One (C) Three (D) Four
Answers
After finding the derivative of f(x) and setting it equal to the average rate of change, we find that there is only one solution in the open interval (0, 1.565). Therefore, the answer is (B) one
To determine the number of values of x in the open interval (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f on the closed interval [0, 1.565], we can use the Mean Value Theorem for Derivatives.
According to the Mean Value Theorem for Derivatives, if f(x) is a differentiable function on the closed interval [a, b], where a < b, then there exists a point c in the open interval (a, b) such that the instantaneous rate of change of f at c is equal to the average rate of change of f on [a, b].
In this case, we are given that the closed interval is [0, 1.565] and the open interval is (0, 1.565), so we need to find if there exists any point c in (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f on [0, 1.565].
To do this, we can first find the average rate of change of f on [0, 1.565] by using the formula:
average rate of change = (f(1.565) - f(0))/(1.565 - 0)
Next, we can find the derivative of f(x) and set it equal to the average rate of change to find any possible values of c that satisfy the Mean Value Theorem for Derivatives.
To learn more about : average
https://brainly.com/question/130657
#SPJ11
The answer is (C) Three, as there will be three points of intersection.
To answer this question, we need to first understand what the instantaneous rate of change and average rate of change mean. The instantaneous rate of change of a function at a particular point is the slope of the tangent line to the graph of the function at that point. The average rate of change of a function over a closed interval is the slope of the secant line connecting the two endpoints of the interval.
In this case, we are looking for values of x in the open interval (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f over the closed interval [0, 1.565].
Since f(x) is not given, we cannot determine the instantaneous and average rate of change of f directly. However, we can use the Mean Value Theorem for Derivatives to help us solve the problem. The Mean Value Theorem states that if f is a continuous function on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists a number c in the open interval (a, b) such that:
f'(c) = (f(b) - f(a))/(b - a)
In this case, we can apply the Mean Value Theorem to the closed interval [0, 1.565] and the open interval (0, 1.565) to get:
f'(c) = (f(1.565) - f(0))/(1.565 - 0)
Simplifying, we get:
f'(c) = f(1.565)/1.565
So, we need to find values of x in the open interval (0, 1.565) where f(x)/x = f(1.565)/1.565.
To solve this equation, we can graph y = f(x)/x and y = f(1.565)/1.565 on the same set of axes and look for points of intersection. The number of intersection points will be the number of values of x in the open interval (0, 1.565) where the instantaneous rate of change of f is equal to the average rate of change of f over the closed interval [0, 1.565].
Therefore, the answer is (C) Three, as there will be three points of intersection.
Visit here to learn more about Mean Value Theorem;
brainly.com/question/30403137
#SPJ11
help fast it's timed please

Answers
Answer:
180 degrees
Step-by-step explanation:
the sum of all the interior angles of a triangle will always be 180 degrees
Answer: 180 degrees
Step-by-step explanation: just search it up and yes it is 180 degrees
Solve using porportions.
3/7 = x/49
Answers
Answer:
x = 21
Step-by-Step Explanation:
3/7 = x/49
49/7 = 7
3*7=21
Elliot adds 15 ml of creamer to 240 ml of coffee. His creamer is 20%
milk fat.
How much pure milk fat has Elliot added to his coffee?
Answers
Answer:
▪ 20% of 15 ml
(20/100) × 15 ml = 3% pure milk fat
Help me solve this problem please sorry if its to small to read but i need help

Answers
Answer:
t4
Step-by-step explanation:
Exponents is basically multiplication. So, if you need to find how much it costs for 4 students then you will multiply tx4.
Let A=(x,y)∈R 2
:x=y and B=(x,y)∈R 2
:x 2
+y 2
=1. Let R=A∪B⊆R 2
be a relation on R. Show that R is reflexive, symmetric, but not transitive, (4 points) 2. Prove that the following relations ∼ are equivalence relations. (a) Let C be the set of continuous functions R→R. Define f∼g on C iff ∃k>0,∃C≥0,∃N≥0,∀x≥N,∣f(x)−g(x)∣≤Clog(kx) (8 points) (b) Let P be the set of non-constant polynomials R→R. Define p∼q on S iff ∃n∈N,∃C>0,∃N≥0,∀x≥N,( p (n)
(x)
≡ constant, q (n)
(x)
≡ constant, and ∣
∣
p (n)
(x)−q (n)
(x) ∣
∣
) Here, the superscript ( n ) means the n-th derivative. ( 8 points )
Answers
The relation p ∼ q is an equivalence relation.
1. R is reflexive:
For reflexive, the elements in A and B should be related to itself.
Here, it is clear that \(x=x\) and \(x^2+y^2=1\) which means each element in A and B is related to itself.
Hence, R is reflexive.
R is symmetric:
For symmetric, the elements in A and B should be related to each other.
Here, it is clear that if (x,y)∈A, then y=x. So, (y,x)∈A.
Therefore, R is symmetric.
R is not transitive:
To show that R is not transitive, we have to give a counterexample.
Let (0,1)∈A and (1,0)∈A.
Here, (0,1) and (1,0) are related to themselves and each other.
But, (0,1) is not related to (1,0) as x≠y and \(x^2+y^2=2\).
Hence, R is not transitive.2.
(a) For f ∼ g to be an equivalence relation, it should be reflexive, symmetric and transitive.
Reflexive:
For reflexive, \(f(x) - g(x) = 0\) when x > N, then it implies that 0 ≤ Clog(kx), and it implies C = 0.
Then, \(f(x) - g(x) = 0\) for all x > N, which implies f(x) = g(x). Hence, f ∼ f.
Therefore, f ∼ f is reflexive.
Symmetric:
For symmetric, we have to show if f ∼ g, then g ∼ f. If f ∼ g, then there exists k > 0, C ≥ 0, N ≥ 0 such that \(|f(x) - g(x)| \leq Clog(kx)\)for all x > N.
Let's call this equation 1. If we reverse the roles of f and g in equation 1, then we get \(|g(x) - f(x)| \leq Clog(kx)\). Hence, g ∼ f. Therefore, f ∼ g is symmetric.
Transitive:
For transitive, we have to show if f ∼ g and g ∼ h, then f ∼ h. If f ∼ g, then there exists k1 > 0, C1 ≥ 0, N1 ≥ 0 such that \(|f(x) - g(x)| \leq C1log(k1x)\) for all x > N1.
Let's call this equation 2. Similarly, if g ∼ h, then there exists k2 > 0, C2 ≥ 0, N2 ≥ 0 such that |g(x) - h(x)| ≤ C2log(k2x) for all x > N2. Let's call this equation 3.
Adding equation 2 and equation 3, we get \(|f(x) - g(x)| + |g(x) - h(x)| \leq C1log(k1x) + C2log(k2x)\) for all x > max(N1, N2).
Since log(a) + log(b) = log(ab), we get \(|f(x) - h(x)| \leq (C1 + C2)log(k1k2x)\) for all x > max(N1, N2).
Hence, f ∼ h. Therefore, f ∼ g is transitive. Hence, f ∼ g is an equivalence relation.
(b) For p ∼ q to be an equivalence relation, it should be reflexive, symmetric and transitive.
Reflexive:
For reflexive, p(x) - q(x) = 0 when x > N, then it implies that \(0 ≤ |p(x) - q(x)| \leq Clog(kx^n)\), and it implies C = 0. Then, p(x) - q(x) = 0 for all x > N, which implies p(x) = q(x).
Hence, p ∼ p. Therefore, p ∼ p is reflexive.
Symmetric:
For symmetric, we have to show if p ∼ q, then q ∼ p. If p ∼ q, then there exists n > 0, C > 0, N ≥ 0 such that |p(n)(x) - q(n)(x)| ≤ C for all x > N.
Let's call this equation 1. If we reverse the roles of p and q in equation 1, then we get |q(n)(x) - p(n)(x)| ≤ C. Hence, q ∼ p. Therefore, p ∼ q is symmetric.
Transitive:
For transitive, we have to show if p ∼ q and q ∼ r, then p ∼ r.
If p ∼ q, then there exists n1 > 0, C1 > 0, N1 ≥ 0 such that \(|p(n1)(x) - q(n1)(x)| \leq C1\) for all x > N1.
Let's call this equation 2.
Similarly, if q ∼ r, then there exists n2 > 0, C2 > 0, N2 ≥ 0 such that \(|q(n2)(x) - r(n2)(x)| \leq C2\) for all x > N2. Let's call this equation 3.
Adding equation 2 and equation 3, we get \(|p(n1)(x) - q(n1)(x)| + |q(n2)(x) - r(n2)(x)| \leq C1 + C2\) for all x > max(N1, N2).
Since \(|p(n1)(x) - q(n1)(x)| \leq |p(n1)(x) - q(n2)(x)| + |q(n2)(x) - q(n1)(x)|\)
and \(|q(n2)(x) - r(n2)(x)| \leq |q(n2)(x) - q(n1)(x)| + |q(n1)(x) - r(n2)(x)|\),
we can rewrite the above inequality as
\(|p(n1)(x) - q(n2)(x)| + |q(n2)(x) - r(n2)(x)| \leq C1 + C2\) for all x > max(N1, N2).
Now, we use the triangle inequality for derivatives,
i.e., \(|f(n)(x) - g(n)(x)| \leq |f(x) - g(x)|\).
Applying this to the above inequality, we get \(|p(x) - r(x)| \leq (C1 + C2)log(kx^n)\) for all x > max(N1, N2).
Hence, p ∼ r. Therefore, p ∼ q is transitive. Hence, p ∼ q is an equivalence relation.
To know more about equivalence relation, visit:
https://brainly.com/question/14307463
#SPJ11
R is reflexive, symmetric, but not transitive. Also, ∼ is an equivalence relation on C and P.
1. (i) R is reflexive if (x, x) ∈ R for every x ∈ R2
For all x ∈ R2, x = x. So, xRx is true. Hence R is reflexive.
(ii) R is symmetric if (y, x) ∈ R whenever (x, y) ∈ R. Suppose that (x, y) ∈ R. Then x = y or
x^2 + y^2 = 1.
Now, in the first case, y = x. Hence (y, x) ∈ R.
If x^2 + y^2 = 1, then we need to show that (y, x) ∈ R.
We have y^2 + x^2 = 1. Therefore, (y, x) ∈ R. Thus R is symmetric.
(iii) R is not transitive because there exist a, b, c ∈ R2 such that (a, b) ∈ R, (b, c) ∈ R, but (a, c) ∉ R.2. We must show that each of the given relations is reflexive, symmetric, and transitive to show that it is an equivalence relation.
(a) Reflexive: Let f(x) be a function in C. Then, for all x ≥ N, |f(x) - f(x)| ≤ C log(kx). Hence, f(x) ~ f(x), and f ~ f.
Symmetric: If f ~ g, then there exists k > 0, C ≥ 0, N ≥ 0 such that |f(x) - g(x)| ≤ C log(kx) for all x ≥ N. Then, |g(x) - f(x)| ≤ C log(kx) for all x ≥ N, and g ~ f.
Transitive: If f ~ g and g ~ h, then there exist k1, k2 > 0, C1, C2 ≥ 0, N1, N2 ≥ 0 such that |f(x) - g(x)| ≤ C1 log(k1x) and |g(x) - h(x)| ≤ C2 log(k2x) for all x ≥ max{N1, N2}.
Therefore, |f(x) - h(x)| ≤ |f(x) - g(x)| + |g(x) - h(x)| ≤ (C1 + C2) log(k1x) + (C1 + C2) log(k2x) = (C1 + C2) log(k1k2x^2) for all x ≥ max{N1, N2}.
Thus, f ~ h. Therefore, ∼ is an equivalence relation on C.
(b) Reflexive: Let p(x) be a non-constant polynomial in P. Then, for all x ≥ N, |p(n)(x) - p(n)(x)| = 0. Hence, p ~ p. Symmetric: If p ~ q, then there exists n ∈ N, C > 0, N ≥ 0 such that |p(n)(x) - q(n)(x)| ≤ C for all x ≥ N. Then, |q(n)(x) - p(n)(x)| ≤ C for all x ≥ N, and q ~ p.
Transitive: If p ~ q and q ~ r, then there exist n1, n2 ∈ N, C1, C2 > 0, N1, N2 ≥ 0 such that |p(n1)(x) - q(n1)(x)| ≤ C1 and |q(n2)(x) - r(n2)(x)| ≤ C2 for all x ≥ max{N1, N2}.
Therefore, |p(n1 + n2)(x) - r(n1 + n2)(x)| = |p(n1)(q(n2)(x)) + q(n1)(q(n2)(x)) - p(n1)(q(n2)(x)) - r(n1)(q(n2)(x))| ≤ |p(n1)(q(n2)(x)) - q(n1)(q(n2)(x))| + |q(n1)(q(n2)(x)) - r(n1)(q(n2)(x))| ≤ (C1 + C2) for all x ≥ max{N1, N2}.
Thus, p ~ r. Therefore, ∼ is an equivalence relation on P.
Conclusion: We have shown that R is reflexive, symmetric, but not transitive. Also, we have shown that ∼ is an equivalence relation on C and P.
To know more about reflexive visit
https://brainly.com/question/24669397
#SPJ11
What will not make a triangle A.11cm,13cm,3cm B.12cm,7cm,5cm C.19cm,14cm,7cm D.2cm,3cm,4cm please help!
Answers
Answer:
B. 12cm,7cm,5cm
Step-by-step explanation:
use triangular inequality therom
A+B>C 12+7>5 true
B+C>A 7+5>12 false
A+C>B 12+5>7 true
One of the sides is not complete so it can not be a triangle.
Answer is option-B
Triangle Inequality Theorem :
In Euclidean geometry, theorem that the sum of any two sides of a triangle is greater than the third side; in symbols,
a + b > c.
a + c > b
b + c > a
(Here)
For option-B
let's take a = 12cm, b = 7cm and c = 5cm.
b + c = a.
It violates triangle Inequality property.
Learn more about Triangle Inequality theorem here: https://brainly.com/question/1163433?referrer=searchResults
#SPJ2
How can I find missing angles measurements ? in complementary angles

Answers
If two angles are complementary, it means that their sum is 90 degrees. This means that
angle FGJ + angle JGH = 90
From the diagram, angle JGH = 24.4
Thus,
angle FGJ + 24.4 = 90
angle FGJ = 90 - 24.4
angle FGJ = 65.6 degrees
What is the diameter of a P210/60R17 tire?
Answers
the diameter of a P210/ 60R17 is 26.9" where width is 8.3" , sidewall 5" overall diameter of the tire is indicated by the first digit.
What is diameter of tire ?Remembering that the tire diameter is made up of two sidewalls—the one above the wheel and the one below the wheel hitting the ground—and adding the diameter of the wheel, the sidewall height must be multiplied by two to determine the tire's overall diameter.
given ,
size = 210 / 60R17
The overall diameter of the tire is indicated by the first digit. The tire diameter or "height" in this illustration is 210 inches tall. The tire's breadth is shown by the second digit. When using tires with inch measurements, the width will typically contain a.50 decimal after the first digit.
the diameter of a P210/ 60R17 is 26.9" where width is 8.3" , sidewall 5"
To know more about diameter of tire visit:-
https://brainly.com/question/22555333
#SPJ1
If a1
= 7 and an
An-1 + 1 then find the value of ac.
Answers
The value of ac can be found by recursively applying the given formula. The formula states that the nth term is equal to the previous term plus 1. Given that a1 = 7, we can calculate the value of ac using this recursive relationship.
To find the value of ac, we need to apply the given formula, which states that each term (except the first term) is equal to the previous term plus 1. Let's start by calculating the second term, a2.
According to the formula, a2 = a1 + 1 = 7 + 1 = 8.
Next, we can calculate the third term, a3, using the same formula. a3 = a2 + 1 = 8 + 1 = 9.
Continuing this process, we can find the values of subsequent terms. a4 = a3 + 1 = 9 + 1 = 10, a5 = a4 + 1 = 10 + 1 = 11, and so on.
By recursively applying the formula, we can determine the value of the nth term. In this case, we are interested in the value of ac. To find it, we need to continue the pattern until we reach the desired term. Since the specific value of c is not provided, we cannot determine the exact value of ac without knowing the value of c. However, we can determine the value of the nth term for any given c by following the recursive formula.
Learn more about recursive relationship:
https://brainly.com/question/22903171
#SPJ11
For an acceptance sampling plan with n = 27 and c = 0, find the probability of accepting a lot that has a defect rate of 4%. (Round your answer to four decimal places.)
Answers
To find the probability of accepting a lot with a defect rate of 4% using an acceptance sampling plan with n = 27 and c = 0, we need to calculate the binomial probability of having zero defects in a sample of 27 items.
The probability of accepting a lot is equal to the probability of having zero defects, which can be calculated using the binomial probability formula. The formula is P(X = k) = C(n, k) * p^k * (1 - p)^(n - k), where P(X = k) is the probability of getting k successes, n is the sample size, p is the probability of success (defect rate), and C(n, k) is the binomial coefficient.
In this case, we want to find P(X = 0) where n = 27 and p = 0.04 (4% defect rate). Substituting these values into the binomial probability formula and calculating it will give us the desired probability of accepting the lot with zero defects.
To learn more about binomial probability click here : brainly.com/question/12474772
#SPJ11
1. 68% of 700
2.85% of 520
3. 40% of 85
4. 32% of 325
5. 2% of 250
6.50% of 104
7. 75% of 396
8. 90% of 80
9. 25% of 64
10. 63% of 400
11.56% of 475
12. 15% of 20
13. 48% of 50
14. 8% of 725
Answers
Answer:
1. 476
2. 442
3. 34
4. 104
5. 5
6. 52
7. 297
8. 72
9. 16
10. 252
11.266
12. 3
13. 24
14. 58
Step-by-step explanation:
Find the difference in the following expression:
(-4c + 5g) - (3c - 8g)
Answers
2.1Simplifying Expressions: Problem 1 (1 point) Simplify the following expression. 6- 4(x - 5)-
Answers
The simplified expression is 26 - 4x.
To simplify the expression 6 - 4(x - 5), we can apply the distributive property and simplify the terms.
6 - 4(x - 5)
First, distribute -4 to the terms inside the parentheses:
6 - 4x + 20
Now, combine like terms:
(6 + 20) - 4x
Simplifying further:
26 - 4x
Therefore, the simplified expression is 26 - 4x.
Learn more about distributive property here
https://brainly.com/question/12192455
#SPJ11
the number of boxes they make for every possible combination is the same. if you randomly choose one of the boxed lunches without knowing the contents, what is the probability you will get an orange and not get juice in your box?
Answers
The probability of randomly selecting a boxed lunch that contains an orange but does not contain juice. The probability of randomly selecting a boxed lunch with an orange is 40%.
In order to calculate the probability, we need more information about the lunch combinations and the distribution of oranges and juice among them. The given statement implies that for every possible combination, the same number of boxes is made. However, we don't know the exact number of combinations or the distribution of oranges and juice within those combinations. Without this information, it is not possible to determine the probability accurately.
To illustrate this, let's consider a simplified example. Suppose there are only two possible combinations: Combination A and Combination B. If there are 10 boxes made for each combination, and Combination A contains 3 boxes with an orange but no juice, while Combination B contains 5 boxes with an orange but no juice, then the probability of randomly selecting a boxed lunch with an orange but no juice would be (3 + 5) / (10 + 10) = 8/20 = 0.4 or 40%.
However, without knowing the specific details of the lunch combinations and the distribution of oranges and juice within those combinations, we cannot determine the probability accurately.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
please answer!
The equation d = 30 − 60h gives the distance d in miles that a bus is from the station h hours after leaving an arena. How far is the station from the arena?
A. 0.5 miles
B. 120 miles
C. 30 miles
D. 60 miles
Answers
Amswer
it is b Step-by-step explanation:
What type of number is -4/2?
Choose all answers that apply:
(Choice A) Whole number
(Choice B) Integer
(Choice C) Rational
(Choice D) Irrational
Answers
Answer:
The type of number that represents -4/2 is:
Choice B) Integer
Choice C) Rational
Step-by-step explanation:
The number -4/2 is an integer because it represents a whole number (-2) and it is also a rational number because it can be expressed as a fraction of two integers.
-4/2 is an :
↬ Integer ↬ Rational numberSolution:
Before we make any decisions about the type of number -4/2 is, let's simplify it first.
It's the same as -2. Now, let's familiarize ourselves with the sets of numbers out there. Where does -2 fit in?
______________
Whole numbersThis set incorporates only positive numbers and zero. So -2 doesn't belong here.
IntegersThis set incorporates whole numbers and negative numbers. So -2 belongs here.
RationalsThis set has integers, fractions, and decimals. So -2 does belong here too.
IrrationalsThis is a set for numbers that cannot be written in fraction form (a/b, where b ≠ 0). So -2 doesn't belong here.
Summary-4/2 belongs in the integer and rationals set.
Hence, Choices B and C are correct.1kg=2,25 pounds. Uncle Makhosi needs 3 and half pounds of butter. Determine the amount of butter in kilograms
Answers
Uncle Makhosi needs approximately 1.56 kilograms of butter.
To determine the amount of butter in kilograms, we'll use the conversion rate of 1 kg = 2.25 pounds.
First, we need to convert 3 and a half pounds to a decimal form. Since half a pound is equal to 0.5 pounds, we can express 3 and a half pounds as 3.5 pounds.
Next, we'll use the conversion rate to calculate the equivalent weight of 3.5 pounds in kilograms:
3.5 pounds * (1 kg / 2.25 pounds) = 1.56 kilograms (rounded to two decimal places).
To summarize, based on the given conversion rate of 1 kg = 2.25 pounds, Uncle Makhosi requires approximately 1.56 kilograms of butter to fulfill his 3 and a half pound requirement. This conversion can be useful when dealing with different units of measurement, allowing us to easily switch between kilograms and pounds.
For more such questions on equivalent weight
https://brainly.com/question/30745781
#SPJ8
1- In Euclidean space, the locus of points equidistant from the origin of a plane is a circle What is the locus of points equidistant (in the spacetime distance seme) from the origin of a spacetime plane? 151 2. A ruler of length L. In at rest in with its left and at the origin. O moves from left to right with speed relative to o along the length of the ruler. The two origins coincide ut time zero for both, at which time a photon is emitted toward the other end of the rulut. What are the coordinates in Olof the event at which the photon maches the other end? (10) 3. The Earth and Alpha Centauri are 43 light years apart. Ignore their relative motion Events A and B occur att on Earth and at 1 year on Alpha Centauri, respectively. (a) What is the time difference between the events according to an observer moving at B - 0.98 from Earth to Alpha Centauri? (b) What is the time difference between the events according to an observer moving at 3 = 0.98 from Alpha Centauri to Earth? (c) What is the speed of a spacecraft that makes the trip from Alpha Centauri to Earth in 2.5 years according to the spacecraft clocks? (d) What is the trip time in the Earth rest frame? [5+5+5+51 + Plane polar coordinates are related to cartesian coordinates by x=rcos and y = rsin. Describe the transformation matrix that maps cartesian coordinates to polar coordinates, and write down the polar coordinate basis vectors in terms of the basis vectors of cartesian coordinates. [51 5- suppose that we are given a basis ei, es consisting of a pair of vectors making a 45° angle with one another, such that ei hus length 2 and ez has length 1. Find the dual basis vectors for the case of covariant components of the vectors. [101
Answers
1. In the context of spacetime, the locus of points equidistant from the origin of a spacetime plane is a hyperbola.
In Euclidean space, the distance between two points is given by the Pythagorean theorem, which only considers spatial dimensions. However, in spacetime, the concept of distance is extended to include both spatial and temporal components. The spacetime distance, also known as the interval, is given by the Minkowski metric:
ds^2 = -c^2*dt^2 + dx^2 + dy^2 + dz^2,
where c is the speed of light, dt represents the temporal component, and dx, dy, dz represent the spatial components.
To determine the locus of points equidistant from the origin, we need to find the set of points where the spacetime interval from the origin is constant. Setting ds^2 equal to a constant value, say k^2, we have:
-c^2*dt^2 + dx^2 + dy^2 + dz^2 = k^2.
If we focus on a spacetime plane where dy = dz = 0, the equation simplifies to:
-c^2*dt^2 + dx^2 = k^2.
This equation represents a hyperbola in the spacetime plane. It differs from a circle in Euclidean space due to the presence of the negative sign in front of the temporal component, which introduces a difference in the geometry.
Therefore, the locus of points equidistant from the origin in a spacetime plane is a hyperbola.
(Note: The explanation provided assumes a flat spacetime geometry described by the Minkowski metric. In the case of a curved spacetime, such as that described by general relativity, the shape of the locus of equidistant points would be more complex and depend on the specific curvature of spacetime.)
To know more about equidistant, refer here:
https://brainly.com/question/29886221#
#SPJ11
help please, and explain(step-by-step) how the answer would be correct.
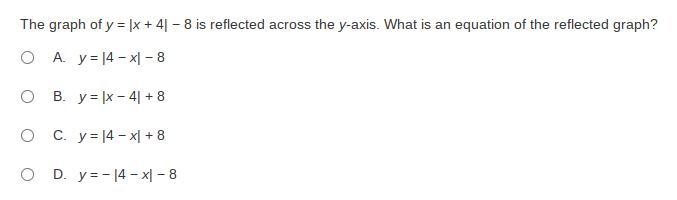
Answers
When a function is reflected, it must be reflected over a line
The new function is: \(y = |4 -x| -8\)
The equation is given as:
\(y = |x + 4| - 8\)
The rule of reflection over the y-axis is:
\((x,y) \to (-x,y)\)
So, we have:
\(y = |-x + 4| -8\)
Rewrite as:
\(y = |4 -x| -8\)
Hence, the new function is:
\(y = |4 -x| -8\)
Read more about reflections at:
https://brainly.com/question/938117
plz help I will give brainiest, how would you solve 4x + 2y = 18 3x - 5y = 20 by elimination showing all of the work and the final answers
note; there are two equations there but they are in the same question
Answers
penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis penis

Suppose that
f(x) = 5 x^6 - 3 x^5.
(A) Find all critical numbers of f. If there are no critical numbers, enter 'NONE'.
Critical numbers =
(B) Use interval notation to indicate where f(x) is increasing.
Note: Use 'INF' for \infty, '-INF' for -\infty, and use 'U' for the union symbol.
Increasing:
(C) Use interval notation to indicate where f(x) is decreasing.
Decreasing:
(D) Find the x-coordinates of all local maxima of f. If there are no local maxima, enter 'NONE'.
x values of local maxima =
(E) Find the x-coordinates of all local minima of f. Note: If there are no local minima, enter 'NONE'.
x values of local minima =
(F) Use interval notation to indicate where f(x) is concave up.
Concave up:
(G) Use interval notation to indicate where f(x) is concave down.
Concave down:
(H) List the x values of all inflection points of f. If there are no inflection points, enter 'NONE'.
x values of inflection points =
(I) Find all horizontal asymptotes of f. If there are no horizontal asymptotes, enter 'NONE'.
Horizontal asymptotes y =
(J) Find all vertical asymptotes of f. If there are no vertical asymptotes, enter 'NONE'.
Vertical asymptotes x =
Answers
The critical value of f(x) = 5x⁶ - 3x⁵ is x = 0.5 which is also its maxima point
f(x) = 5x⁶ - 3x⁵
differentiation w.r.t x
=> f'(x) = 30x⁵ - 15x⁴
Putting f'(x) = 0
30x⁵ - 15x⁴ = 0
=> x⁴(30x - 15) =0
=> 30x - 15 = 0
=> x = 15/30
=> x = 0.5 , 0
Critical number is 0.5 , 0
(B) To find where f(x) is increasing
for x > 0.5 ,
(30x-15) > 0 => x⁴(30x - 15) > 0
Therefore , f(x) is increasing at ( 0.5 , ∞ )
(C)To find where f(x) is decreasing
for x < 0.5 ,
(30x-15) < 0 => x⁴(30x - 15) < 0
Therefore , f(x) is decreasing at ( -∞ , 0.5)
(D) Differentiation f'(x) again w.r.t to x
f'(x) = 30x⁵ - 15x⁴
f"(X) = 150x⁴ - 60x³
Substituting critical values of x
=> 150(0.5)⁴ - 60(0.5)³
=>9.375 - 7.5
=> -1.875 < 0 , Hence , x = 0.5 is point of maxima
(E) no point of minima
Similarly , we can solve other parts
To know more about Function here
https://brainly.com/question/28303908
#SPJ4
Evaluate: f(x) = x + 7
a. f(5) =
b. f(-1) =
c. f(-3) =
Answers
Answer:
Step-by-step explanation:
a. f(5) = 5+7 = 12
b. f(-1) = -1+7 =6
c. f(-3) = -3+7 =4
b. -1+7=6
c. -3+7=4
why can it be difficult to interpret a correlation between two variables?
Answers
Interpreting a correlation requires careful consideration of factors such as causation, confounding variables, nonlinearity, outliers, and sample characteristics.
Interpreting a correlation between two variables can be difficult for several reasons:
Causation vs. correlation: Correlation measures the strength and direction of the relationship between two variables but does not imply causation. Just because two variables are correlated does not mean that one variable causes the other. It is essential to avoid making causal claims based solely on correlation.
Confounding variables: Correlations can be influenced by the presence of confounding variables that affect both variables being studied. Without accounting for these confounding factors, it can be challenging to determine the true nature of the relationship between the variables of interest.
Nonlinear relationships: Correlation coefficients, such as Pearson's correlation coefficient, measure linear relationships between variables. If the relationship is nonlinear, the correlation may not accurately capture the association. It is crucial to consider other types of analysis or transformations to capture more complex relationships.
Outliers and influential observations: Extreme values or outliers in the data can have a significant impact on correlation coefficients. These outliers may distort the correlation and lead to incorrect interpretations. It is important to examine the data for influential observations that may unduly influence the correlation results.
Sample size and representativeness: The size and representativeness of the sample can affect the reliability and generalizability of correlation results. Small or biased samples may not provide a representative picture of the population, leading to misleading interpretations.
Overall, it is important to use correlations as part of a broader analysis and consider additional evidence before drawing definitive conclusions about the relationship between variables.
Learn more about variables at: brainly.com/question/15078630
#SPJ11
Please can someone answer this question it would be much appreciated
Thanks so much :)



Answers
I need help too on this one
Answer:
you lowest tempeture in the mesosphere is -96
Step-by-step explanation:
The graph 4x^2-4x-1 is shown. Use the grpah to find the estimates for the solutions of 4x^2-4x-1=0 and 4x^2 - 4x-1=2

Answers
Answer:
a) The estimates for the solutions of \(4\cdot x^{2}-4\cdot x -1 = 0\) are \(x_{1}\approx -0.25\) and \(x_{2} \approx 1.25\).
b) The estimates for the solutions of \(4\cdot x^{2}-4\cdot x -1 = 2\) are \(x_{1}\approx -0.5\) and \(x_{2} \approx 1.5\)
Step-by-step explanation:
From image we get a graphical representation of the second-order polynomial \(y = 4\cdot x^{2}-4\cdot x -1\), where \(x\) is related to the horizontal axis of the Cartesian plane, whereas \(y\) is related to the vertical axis of this plane. Now we proceed to estimate the solutions for each case:
a) \(4\cdot x^{2}-4\cdot x -1 = 0\)
There are two approximate solutions according to the graph, which are marked by red circles in the image attached below:
\(x_{1}\approx -0.25\), \(x_{2} \approx 1.25\)
b) \(4\cdot x^{2}-4\cdot x -1 = 2\)
There are two approximate solutions according to the graph, which are marked by red circles in the image attached below:
\(x_{1}\approx -0.5\), \(x_{2} \approx 1.5\)
