11/13% of a quantity is equal to what fraction of the quantity?
Answers
11/13% of a quantity is equal to 11/1300 fraction of the quantity.
What is Percent to Fraction?Percentage signifies for every hundred or for each. We display it as %. Since a percentage is expressed on a scale of 1 to 100, it is easy to comprehend. Converting percentage data to fractions is known as "percent to a fraction." As per the percent to fraction conversion instructions, the percentage can be written as a fraction by deleting the percent symbol and placing 100 in the denominator. Any percent can easily be converted to a fraction, and the opposite is also true.
How to Convert Percent to Fraction?To convert a percentage to a fraction, follow these three simple steps. Let's examine these three processes in more detail.
Leave out the percent sign.divide it by 100.Reduce the obtained fraction.Divide the given percentage by 100
\(\frac{11}{13}\)% \(=\frac{11}{13} \times \frac{1}{100} \\=\frac{11}{1300}\)
To know more about percent to fraction conversion uses, visit:
https://brainly.com/question/16763182
#SPJ9
Related Questions
Janelle is building a wooden playhouse, and she needs to cut a board such that it forms angles A and B , where the measure of angle A is 13 of the measure of angle B , and angles A and B are supplementary. What is the measure of angle B ?
Answers
Using the concept of supplementary angles, it is found that the measure of angle B is of 135º.
--------------------------------
If two angles are supplementary, the sum of their measures is of 180º.A and B are supplementary, thus:\(A + B = 180\)
The measure of angle A is 1/3 of the measure of angle B, thus:\(A = \frac{B}{3}\)
Replacing in the equation for the sum:
\(A + B = 180\)
\(\frac{B}{3} + B = 180\)
\(B + 3B = 540\)
\(4B = 540\)
\(B = \frac{540}{4}\)
\(B = 135\)
The measure of angle B is of 135º.
A similar problem is given at https://brainly.com/question/22826236
If X is uniformly distributed over (0,1) and Y is exponentially distributed with parameter λ = 1, find the distribution of (a) (5 points) Z=X+Y (b) (5 points) Z=X/Y
Answers
a. The distribution of Z=X+Y is fZ(z) = 0
b. The distribution of Z=X/Y is a constant distribution with fZ(z)
To find the distribution of Z in both cases, we need to use the concept of convolution for the sum of random variables.
(a) Z = X + Y:
Since X is uniformly distributed over (0,1) and Y is exponentially distributed with parameter λ = 1, we can find the distribution of Z by convolving the probability density functions (PDFs) of X and Y.
The PDF of X is a constant function over the interval (0,1) and is given by:
fX(x) = 1, for 0 < x < 1
fX(x) = 0, otherwise
The PDF of Y, being exponentially distributed with parameter λ = 1, is given by:
fY(y) = λ * exp(-λy), for y > 0
fY(y) = 0, otherwise
To find the distribution of Z, we convolve the PDFs of X and Y:
fZ(z) = ∫ fX(z-y) * fY(y) dy
= ∫ 1 * exp(-y) dy, for z-1 < y < z
Integrating the above expression:
fZ(z) = [-exp(-y)] from z-1 to z
= exp(-(z-1)) - exp(-z), for 1 < z < 2
= 0, otherwise
Therefore, the distribution of Z = X + Y is given by:
fZ(z) = exp(-(z-1)) - exp(-z), for 1 < z < 2
fZ(z) = 0, otherwise
(b) Z = X/Y:
To find the distribution of Z, we can use the method of transformation of random variables.
Let's define W = X/Y. We can find the cumulative distribution function (CDF) of W, and then differentiate to obtain the PDF.
The CDF of W can be expressed as:
FZ(z) = P(Z ≤ z) = P(X/Y ≤ z)
To proceed, we'll consider two cases separately:
Case 1: z > 0
In this case, we have:
FZ(z) = P(X/Y ≤ z) = P(X ≤ zY) = ∫[0,1] ∫[0,zy] 1 dy dx
= ∫[0,1] zy dy dx
= z ∫[0,1] y dy dx
= z [y^2/2] from 0 to 1
= z/2
Case 2: z ≤ 0
In this case, we have:
FZ(z) = P(X/Y ≤ z) = P(X ≥ zY) = 1 - P(X < zY) = 1 - ∫[0,1] ∫[0,zy] 1 dy dx
= 1 - ∫[0,1] zy dy dx
= 1 - z ∫[0,1] y dy dx
= 1 - z [y^2/2] from 0 to 1
= 1 - z/2
Therefore, the CDF of Z = X/Y is:
FZ(z) = z/2, for z > 0
FZ(z) = 1 - z/2, for z ≤ 0
Differentiating the CDF, we obtain the PDF:
fZ(z) = 1/2, for z > 0
fZ(z) = 1/2, for z ≤ 0
Therefore, the distribution of Z = X/Y is a constant distribution with fZ(z)
Learn more about distribution at https://brainly.com/question/15707574
#SPJ11
f(x)=-6(x+5) find the value of f(4) for the function
Answers
Answer:
-54
Step-by-step explanation:
For this question, all you have to do it plug 4 in for x.
-6(4+5)
-6(9)
-54
hi I was wondering if you could confirm why the limit is 0

Answers
Hello there. To solve this question, we have to remember some properties about limits.
Given the following limit:
\(\begin{gathered} \lim_{x\to\infty}\dfrac{\cos(5x)}{x} \\ \end{gathered}\)We want to determine its value.
For this, we'll use the "sandwich" theorem, that is also called as the squeeze theorem.
Notice that
\(-1\leq\cos(5x)\leq1\)Hence dividing both sides of the equation by a factor of x, we'll get
\(-\dfrac{1}{x}\leq\dfrac{\cos(5x)}{x}\leq\dfrac{1}{x}\)Taking the limit as x goes to infinity (and of course this works for x very large), it wouldn't work if we were to determine the value at 0.
\(\lim_{x\to\infty}-\dfrac{1}{x}\leq\lim_{x\to\infty}\dfrac{\cos(5x)}{x}\leq\lim_{x\to\infty}\dfrac{1}{x}\)The left and right hand side limits are equal to zero, hence
\(0\leq\lim_{x\to\infty}\dfrac{\cos(5x)}{x}\leq0\)And this is precisely the value of this limit:
\(\lim_{x\to\infty}\dfrac{\cos(5x)}{x}=0\)The domestic violence study conducted in 1984 by Sherman and Berk had an ethical concern in that: O They financially profited from the research. O They did not adhere to special protections for vulnerable populations. O They potentially withheld a beneficial treatment. O They deceived their subjects.
Answers
In the 1984 domestic violence study conducted by Sherman and Berk, the ethical concern was that they potentially withheld a beneficial treatment.
The domestic violence study conducted by Sherman and Berk in 1984 raised an ethical concern in that they financially profited from the research. This raises the question of whether their motives were purely altruistic or whether they were driven by financial gain. Additionally, the study did not adhere to special protections for vulnerable populations such as women and children who may have been victims of domestic violence. This raises concerns about the validity and generalizability of the study's findings. Furthermore, the study potentially withheld a beneficial treatment, which raises questions about the ethical responsibility of researchers to ensure that their subjects receive the best possible care. Finally, there are also concerns that the researchers may have deceived their subjects, which raises questions about the integrity and transparency of the research process. In conclusion, the ethical concerns raised by this study highlight the need for researchers to carefully consider the impact of their research on vulnerable populations and to ensure that they adhere to the highest ethical standards.
Visit here to learn more about ethical concerns:
brainly.com/question/28318353
#SPJ11
determine the equation of the circle graphed below.
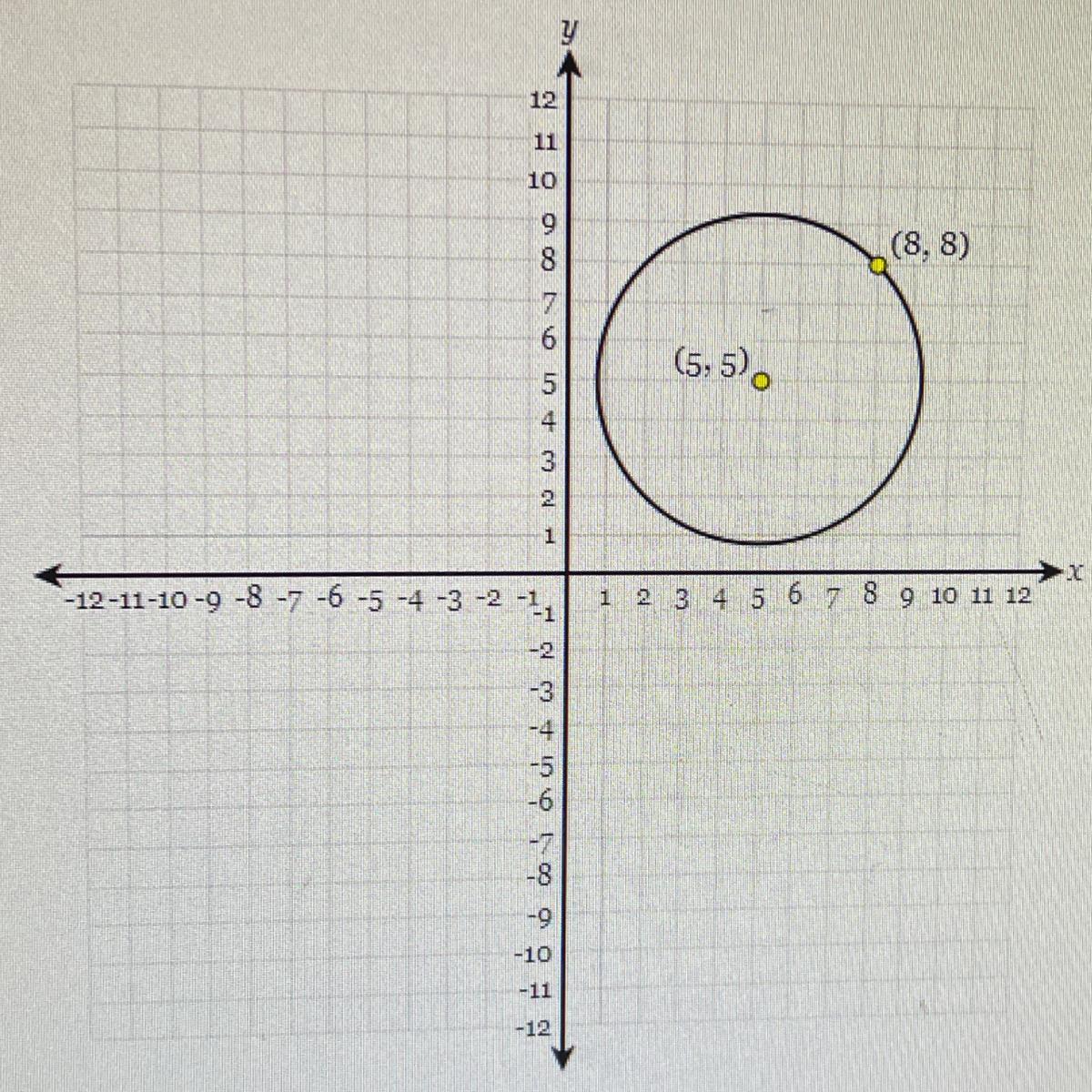
Answers
Answer:
(x - 5)² + (y - 5)² = 18
Step-by-step explanation:
The equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k) are the coordinates of the centre and r is the radius
Here (h, k ) = (5, 5) , then
(x - 5)² + (y - 5)² = r²
r is the distance from the centre to a point on the circle
Calculate r using the distance formula
r = \(\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\)
with (x₁, y₁ ) = (5, 5) and (x₂, y₂ ) = (8, 8)
r = \(\sqrt{(8-5)^2+(8-5)^2}\)
= \(\sqrt{3^2+3^2}\)
= \(\sqrt{9+9}\)
= \(\sqrt{18}\) ⇒ r² = (\(\sqrt{18}\) )² = 18
Then
(x - 5)² + (y - 5)² = 18 ← equation of circle
A ball is thrown in the air. The function H = 30t - 5t^2 can be used to find the height (H) of the ball in meters after t seconds.
How long does it take the ball to reach a height of 45 meters?
Answers
The ball to rise 45 meters in 3 seconds.
How do you find the solutions of a quadratic equation?
Put the equal sign with all terms on one side and zero on the other.Factor.Each factor should be set to zero.Fix each of these problems.Put your solution into the original equation to make sure.Since these are the values of x for which f(x) = 0, the roots of the function f(x) = ax2 + bx + c correspond to the solutions of the quadratic equation ax2 + bx + c = 0.Depending on the sign of the discriminant, there are always either 0, 1, or 2 real solutions to a quadratic equation. However, if you include both real and complex numbers, there is always at least one answer.here
Function : \(H= 30t-5t^{2}\)
height = 45m
then \(30t-5t^{2} = 45\)
simplify the quadratic equation ⇒ \(6t-t^{2} -9=0\)
⇒ \(t^{2} -6t+9=0\)
⇒ \((t-3) (t-3)=0\\t=3.\)
time required to reach 45m = 3 sec.
To learn more about : Quadratic equation
Ref : https://brainly.com/question/1214333
#SPJ13
While measuring the side of a cube, the percentage error incurred was 3%. Using differentials, estimate the percentage error in computing the volume of the cube. 9% O 6% O 0.09% O 0.06%
Answers
the estimated percentage error in computing the volume of the cube is approximately 3%.
To estimate the percentage error in computing the volume of a cube using differentials, we can use the concept of differentials and relative error.
Let's denote the side length of the cube as "s" and the volume of the cube as "V". The given percentage error in measuring the side length is 3%. This means that the relative error in the side length is 3/100 = 0.03.
Using differentials, we can express the change in volume (dV) in terms of the change in side length (ds) as:
dV = 3s² ds
To estimate the percentage error in computing the volume, we divide the change in volume (dV) by the original volume (V) and multiply by 100 to express it as a percentage. So, we have:
Percentage error in volume = (dV / V) * 100Substituting the values:
Percentage error in volume = [(3s² ds) / (s³)] * 100
Simplifying:
Percentage error in volume = (3 / s) * ds * 100
Since we are estimating the percentage error, we can ignore the "ds" term since it represents a small change in the side length. Therefore, we have:
Percentage error in volume ≈ (3 / s) * 100
Now, let's substitute the given percentage error in measuring the side length as 3%:
Percentage error in volume ≈ (3 / s) * 100 ≈ (3 / 100) * 100 ≈ 3%
To know more about volume visit:
brainly.com/question/28058531
#SPJ11
If the population standard deviation of a sample increases without other changes, what is most likely to happen to the confidence interval?
Answers
If the population standard deviation of a sample increases without other changes, the confidence interval is most likely to widen.
This is because the standard deviation is a measure of the spread of the data, so if it increases, the data points are more spread out from the mean. As a result, the range of values that could reasonably contain the true population parameter (i.e., the confidence interval) needs to be wider to account for the increased variability in the sample.
If the population standard deviation of a sample increases without other changes, the confidence interval is most likely to become wider.
When standard deviation increases, it indicates more variability in the data. As a result, the confidence interval, which is a range of values that estimates the true population parameter with a certain level of confidence, needs to be wider to account for the increased variability. This ensures that the true population parameter is still captured within the interval with the same level of confidence.
Visit here to learn more about standard deviation:
brainly.com/question/23907081
#SPJ11
A, B and C are points on the circumference of a circle.
XY is a tangent to the circle at the point A.
Angle BAY = 72° and angle ABC = 54°.
Prove that triangle ABC is an isosceles
triangle.
You must give a reason for any statement
that you make or any calculation that you
carry out.
Answers
By using tangent property of circle, it has been proved that \(\Delta\) ABC is isosceles
What is tangent to a circle?
At first it is important to know about circle.
Circle is a two dimensional round figure in which every point of the circle maintains a fixed distance from a point known as the center. The fixed distance is called the radius of the circle.
The straight line which touches the circle at any point is known as the tangent to a circle.
Tangent property of circle is used here
\(\angle BAY = 72^{\circ}\)
\(\angle ABC = 54^{\circ}\)
\(\angle ACB = 72^{\circ}\) [Angle in alternate segment are equal]
\(\angle BAC = 180 - (54 + 72)\\\) [Sum of three angles of a triangle is 180°
= 180 - 126
= 54°
\(\Delta ABC\) is isosceles
To learn more about tangent of a circle, refer to the link-
https://brainly.com/question/16507124
#SPJ9
What is the range of the function y = x² + 1?
Answers
Answer
[ 1 by 2, -1 by 2 ]
Step-by-step explanation:
https://haygot.s3.amazonaws.com/questions/1118559_1200733_ans_2ec06a240d2240e49dc1c9fda7b41ef5.jpeg
Answer:
range { 1, ∞ }
Step-by-step explanation:
y = x² + 1
is a parabola with its vertex at (0, 1)
The range is { 1, ∞ }
to find the product 203 times 197 without a calculator, priya wrote (200 3)(200-3) very quickly, and without writing anything else, she arrived at 39,991. explain how writing the two factors as a sum and a difference may have helped priya.
Answers
Priya arrived at the product 203 times 197, which is 39991, by utilizing the difference of squares formula. This approach allowed her to perform the calculation mentally and quickly without the need for a calculator.
Writing the two factors (203 and 197) as a sum and a difference, Priya used the difference of squares formula. The formula states that the product of a sum and a difference of two numbers is equal to the square of the first number minus the square of the second number.
In this case, Priya wrote (200 + 3)(200 - 3) instead of directly multiplying 203 and 197. By doing so, she was able to take advantage of the difference of squares formula.
Expanding the expression (200 + 3)(200 - 3) gives:
(200 + 3)(200 - 3) = 200^2 - 3^2
Now, simplifying further:
200^2 - 3^2 = 40000 - 9 = 39991
know more about squares formula here:
https://brainly.com/question/18294904
#SPJ11
can you help solve for y?

Answers
Answer:
Go ahead and color the nose red!
The solution is
\(y = \dfrac{n-9}{x}\)
Step-by-step explanation:
\(\text{We have: }\\\\\)
\(\rightarrow\; \dfrac{x}{y} + 9 = n\\\\\\\text{Subtract 9 from both sides:}\\\\\rightarrow\;\dfrac{x}{y} + 9 - 9 = n - 9\\\\\)
\(\rightarrow\;\dfrac{x}{y} = n - 9\\\\\)
Multiply both sides by y:
\(\rightarrow\; y \cdot \dfrac{x}{y} = y (n-9)\\\\\rightarrow\; x = y(n-9)\\\\\\\)
\(\text{Divide both sides by (n-9)}:\\\\\\\rightarrow\; \dfrac{x}{n-9} = \dfrac{y (n-9)}{n-9}\\\\\\\rightarrow\; \dfrac{x}{n-9} = y\\\\\\\)
By switching sides without changing the meaning, this can be re-written as :
\(y = \dfrac{x}{n-9} \\\\\)
which of course means you can color the nose red
:)
Mark and Allen were assigned the same book to read for class. Mark started reading on Saturday , and he is reading 40 pages per day. Allen didn't start until Sunday , but he is still reading 45 pages a day.
How many days will it take Allen to catch up to Mark, and how many pages will they each have read?
Let x represent the number of days Allen has been reading.
Answers
Given:
Mark started reading on Saturday , and he is reading 40 pages per day.
Allen didn't start until Sunday , but he is still reading 45 pages a day.
To find:
How many days will it take Allen to catch up to Mark, and how many pages will they each have read?
Solution:
Let \(x\) represent the number of days Allen has been reading. Then the number of days Mark has been reading is \((x+1)\).
Mark is reading 40 pages per day. So, he will read \(40(x+1)\) pages.
Allen is reading 45 pages a day. So, he will read \(45x\) pages.
Allen catch up to Mark when they read equal number of pages.
\(40(x+1)=45x\)
\(40x+40=45x\)
\(40=45x-40x\)
\(40=5x\)
Divide both sides by 5.
\(\dfrac{40}{5}=\dfrac{5x}{5}\)
\(8=x\)
In 8 days Allen will catch up to Mark.
\(45x=45(8)\)
\(45x=360\)
Therefore, they each have read 360 pages.
Are vertical lines negative?
Answers
Vertical lines do not have positive slopes or negative slopes. They have undefined slopes.
Now, According to the question :
What is Vertical line?
A vertical line is a line, parallel to y-axis and goes straight, up and down, in a coordinate plane. Whereas the horizontal line is parallel to x-axis and goes straight, left and right.
Is a vertical line positive or negative?
The slope of a line can be positive, negative, zero, or undefined. A horizontal line has slope zero since it does not rise vertically (i.e. y1 − y2 = 0), while a vertical line has undefined slope since it does not run horizontally (i.e. x1 − x2 = 0).
Hence, Vertical lines do not have positive slopes or negative slopes. They have undefined slopes.
Learn more about Vertical line at:
https://brainly.com/question/13425491
#SPJ4
Write the coordinates of the vertices after a rotation 270° counterclockwise around the origin.
T=
U=
V=
W=

Answers
The coordinates of the vertices after a rotation 270° counterclockwise around the origin will be:
T'(-8, -4) , U'(-8, -6) , V'(-3, -9) , W'(-3, -7)
When a point P(x, y) is rotated 270° counterclockwise around the origin, we flip x and y and reverse the sign of x.
Thus,
The rule to rotate a point P(x, y) after a rotation 270° counterclockwise around the origin is:
P(x, y) → P'(y, -x)
From the Graph,
In our case, we have the points
T = (4, -8)
U = (6, -8)
V = (9, -3)
W = (7, -3)
Thus, the coordinates of the vertices after a rotation 270° counterclockwise around the origin will be:
P(x, y) → P'(y, -x)
T (4, -8) → T'(-8, -4)
U (6, -8) → U'(-8, -6)
V (9, -3) → V'(-3, -9)
W (7, -3) → W'(-3, -7)
Therefore, the coordinates of the vertices after a rotation 270° counterclockwise around the origin will be:
T'(-8, -4) , U'(-8, -6) , V'(-3, -9) , W'(-3, -7)
Learn more about Graph at
https://brainly.com/question/10712002
#SPJ1
17. of a pound of fruit for $15
Answers
Answer:
40
Step-by-step explanation:
37.5% × ? = 15 =>
? =
15 ÷ 37.5% =
15 ÷ (37.5 ÷ 100) =
(100 × 15) ÷ 37.5 =
1,500 ÷ 37.5 =
40
Help I suck at this Please Help Me!

Answers
By using partial products to multiply, 52 × 6 is 312
Multiplying using partial productsFrom the question, we are to use partial products to multiply 52 × 6
The partial multiplication is shown below
5 2
× 6
300 6 × 5 tens (That is, 6 × 5 × 10 = 300)
+ 12 6 × 2 ones (That is, 6 × 2 × 1 = 12)
312
Hence, by using partial products to multiply, 52 × 6 is 312
Learn more on Multiplying using partial products here: https://brainly.com/question/877212
#SPJ1
Multiply 2x(x^2-x+3)

Answers
Answer:
2x^3-2x^2+6x
Step-by-step explanation:
Hope this helps!
Have a great day!
Answer:
2x^3-2x^2+3
don't know if it's correct
Consider the rotated ellipse defined implicitly by the equation &r? + 4xy + 5y = 36. + The quadratic form can be written as [x v1[=Lx y Por[j] = { vo[] where P Hint: What is special about the columns of P? Can you use this to find the matrix ? Once you find D you can plug it into the equation above and perform matrix multiplication to find the answer to part (a)! a. Using the P defined above, find an equation for the ellipse in terms of u and v. Don't forget to enter the right-hand side too! b. Now drag the points to display the graph of your ellipse on the an-axes below. 3 2 -intercept -intercept 3 6 -2 -3 4 c. Finally, give the (x,y) locations of the vertices you have just located. Convert the vertex on the n-axis to (x,y) coordinates. lii. Convert the vertex on the v-axis to (X.) coordinates.
Answers
The vertex on the n-axis is (0, 6/√34) and the vertex on the v-axis is (6/√34,0).
Given the rotated ellipse defined implicitly by the equation,
r² + 4xy + 5y² = 36.
The quadratic form can be written as [x y][4,2;2,5][x y]
T = [u v]
We can write [4,2;2,5] as D.
We can write the equation as [x y]PDP^(-1)[x y]T = [u v]
where P = [cos(theta) -sin(theta); sin(theta) cos(theta)] and
tan(2*theta) = 4/3
Now, we have to find D.
We have [4,2;2,5] = [cos(theta) -sin(theta);
sin(theta) cos(theta)][d1 0;0 d2][cos(theta) sin(theta);
-sin(theta) cos(theta)]
Let [4,2;2,5] = A , [cos(theta) -sin(theta);
sin(theta) cos(theta)] = P and [cos(theta) sin(theta);
-sin(theta) cos(theta)] = Q.
Then, A = PQDP^(-1)Q^(-1)
So, D = P^(-1)AP
= [1/2 1/2;-1/2 1/2][4,2;2,5][1/2 -1/2;-1/2 1/2]
= [3 0;0 6]
So, we have [x y][1/2 1/2;-1/2 1/2][3 0;0 6][1/2 -1/2;-1/2 1/2]
[x y]T = [u v]
Now, we have [u v] = [x y][3/2 3/2;-3/2 3/2][x y]T
The equation of the ellipse is (3x+3y)² + (-3x+3y)² = 36.
So, we get 9x² + 18xy + 9y² = 36.
Now, we have to drag the points to display the graph of the ellipse on the axes.
\( \left(\frac{6}{\sqrt{34}}, 0\right)\), \( \left(-\frac{6}{\sqrt{34}}, 0\right)\),\( \left(0,\frac{6}{\sqrt{34}}\right)\),\( \left(0,-\frac{6}{\sqrt{34}}\right)\),\( \left(\frac{3}{\sqrt{34}},\frac{3}{\sqrt{34}}\right)\),\( \left(-\frac{3}{\sqrt{34}},-\frac{3}{\sqrt{34}}\right)\),\( \left(\frac{3}{\sqrt{34}},-\frac{3}{\sqrt{34}}\right)\),\( \left(-\frac{3}{\sqrt{34}},\frac{3}{\sqrt{34}}\right)\).
The vertices are (3/√34,3/√34), (-3/√34,-3/√34), (3/√34,-3/√34), (-3/√34,3/√34) and the intersections with the x and y-axis are \( \left(\frac{6}{\sqrt{34}}, 0\right)\), \( \left(-\frac{6}{\sqrt{34}}, 0\right)\),\( \left(0,\frac{6}{\sqrt{34}}\right)\),\( \left(0,-\frac{6}{\sqrt{34}}\right)\).
Therefore the solution is as follows:
a. The equation of the ellipse in terms of u and v is (3u/2)² + (3v/2)² = 36/4 = 9.
b. The graph is displayed below.
c. The (x, y) locations of the vertices are given by (3/√34,3/√34), (-3/√34,-3/√34), (3/√34,-3/√34), (-3/√34,3/√34).
The vertex on the n-axis is (0, 6/√34) and the vertex on the v-axis is (6/√34,0).
To know more about ellipse visit
https://brainly.com/question/9702250
#SPJ11
Mechanical energy is as much of potential and kinetic energy. Mechanical energy is never lost but only transformed from one form to another. As long as all the mechanical energy is as much as the potential energy then the kinetic energy is 0J. The mechanical energy of an object is found by summing its potential energy and kinetic energy.
Answers
Given the matrices A=[[-3,4],[5,-5]],B=[[-1,1],[2,-1]], and C=[[2,4],[2,0]], solve for the matrix x in the equation (A-5B)x=C.
Answers
The solution to the equation (A-5B)x = C is x = [[2/5, 0], [0, -2/5]].
To solve for the matrix x in the equation (A-5B)x = C, we need to first calculate the matrix (A-5B) and then solve the equation using matrix operations.
Given matrices:
A = [[-3, 4], [5, -5]]
B = [[-1, 1], [2, -1]]
C = [[2, 4], [2, 0]]
To calculate the matrix (A-5B), we subtract 5 times each element of matrix B from the corresponding element of matrix A:
A-5B = [[-3, 4], [5, -5]] - 5[[-1, 1], [2, -1]]
= [[-3, 4], [5, -5]] - [[-5, 5], [10, -5]]
= [[-3 + 5, 4 - 5], [5 - 10, -5 + 5]]
= [[2, -1], [-5, 0]]
Now, we can solve the equation (A-5B)x = C by multiplying both sides of the equation by the inverse of (A-5B):
(A-5B)^(-1)(A-5B)x = (A-5B)^(-1)C
x = (A-5B)^(-1)C
To find the inverse of the matrix (A-5B), we calculate the inverse of [[2, -1], [-5, 0]]:
(A-5B)^(-1) = [[2, -1], [-5, 0]]^(-1)
= [[0, 1/5], [-1/2, 2/5]]
Finally, we can substitute the values into the equation to find the matrix x:
x = [[0, 1/5], [-1/2, 2/5]] * [[2, 4], [2, 0]]
= [[(02)+(1/52), (04)+(1/50)], [(-1/22)+(2/52), (-1/24)+(2/50)]]
= [[2/5, 0], [0, -2/5]]
Therefore, the solution to the equation (A-5B)x = C is x = [[2/5, 0], [0, -2/5]].
learn more about equation here
https://brainly.com/question/29657983
#SPJ11
the coordinates of the vertices of parallelogram QRST are given. What would be the coordinates of the vertices after a dilation with a scale factor of 1/3 centered at the origin Q (-6,9) R (6,9) S (0,-9) T (-12,-9)
Answers
Answer -2,3. 2,3 3,-3 -4 -3
Step-by-step explanation:
Answer:
Q (-2, 3)
R (2, 3)
S (3, -3)
T (-4, -3)
Step-by-step explanation:
Good luck kiddos :)
Determine all values of h and f for which the system x + 3y = h and -4x + ky = -9 has no solution.
Answers
For any price of h and k = -12, the system x + 3y = h and -4x + ky = -9 will haven't any answer.
To determine the values of h and okay for which the device of equations has no answer, we want to locate the situations underneath which the equations are inconsistent or parallel.
The given system of equations is:
Equation 1: x + 3y = h
Equation 2: -4x + ky = -9
For the gadget to haven't any answer, the lines represented with the aid of these equations should be parallel and in no way intersect. In different phrases, the slopes of the traces need to be equal, but the y-intercepts should be specific.
Let's first discover the slopes of the traces. The slope-intercept form of Equation 1 is y = (-1/3)x + (h/3), wherein the slope is -1/3. The slope-intercept shape of Equation 2 is y = (4/k)x - (9/k), wherein the slope is 4/k.
For the strains to be parallel, the slopes should be equal. Therefore, we have the condition: -1/3 = 4/k.
To locate the values of h and okay for which the gadget has no answer, we need to locate the values of h that satisfy the situation -1/3 = 4/k.
Solving this equation for ok, we've got:
-1/3 = 4/k
-1 = 12/k
k = -12
Substituting k = -12 returned into the equation -1/3 = 4/k, we've:
-1/3 = 4/(-12)
-1/3 = -1/3
Since the equation holds real for any value of h, there aren't any restrictions at the price of h.
Therefore, for any price of h and k = -12, the system x + 3y = h and -4x + ky = -9 will haven't any answer.
To know more about equations,
https://brainly.com/question/29797709
#SPJ4
The system of equations has no solution when k is equal to 12. The value of h can be any real number.
To determine the values of h and f for which the system has no solution, we need to analyze the coefficients of the variables and the constants in the equations.
The given system of equations is:
x + 3y = h
-4x + ky = -9
We can rewrite the second equation as:
-4x + ky = -9
Dividing both sides of the equation by -4, we get:
x - (k/4)y = 9/4
Comparing the coefficients of x and y in the two equations, we can see that the slopes of the lines represented by the equations are different when k is not equal to 12.
Therefore, for the system to have no solution, k must be equal to 12.
As for the value of h, it can be any real number since it does not affect the slopes of the lines.
Learn more:About system of equations here:
https://brainly.com/question/21620502
#SPJ11
LOTS OF POINTS
answer the question down below correctly
thanks

Answers
Answer:
y = 1x + 2
Step-by-step explanation:
To fill in slope intercept form(y = mx + b) identify the initial value(b) and slope(m).
The initial value is the y coordinate when the x coordinate is 0. It is also known as the point where the line crosses the y axis. This point on the graph is (0, 2). So, the initial value is 2.
Slope is identified by finding a point on the graph that the line passes through and creating a right triangle to a point that is even with both point. Then, divide the y coordinate of that point by its x coordinate. One coordinate you could use is point (-2, 2). 2 divided by -2 is -1. But, since the line has a positive association, the slope is going to be a positive number. So, the slope is 1.
Now fill in the the slope intercept form.
y = mx + b ---> y = 1x + 2
Answer:
y= X + 2
Step-by-step explanation:
After 4 minutes of reading, Aaron was on page 14 of his book. After 8 minutes he was on page 20. Which equation models the page number, y, in terms of minutes x?
Group of answer choices
y = 8x + 1.5
y = 1.5x + 8
y = −1.5x + 8
y = –8x + 1.5
Answers
Answer:
The answer would be (B) y = 1.5x + 8
Step-by-step explanation:
The equation that models the number of pages (y) and number of minutes (x) is y = 1.5x + 8.
What is Equation Modelling?Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.
Given is Aaron who is reading a book. After 4 minutes of reading, Aaron was on page 14 of his book and after 8 minutes he was on page 20.
Now -
(x) represents the number of minutes and (y) is the number of pages.
At x = 4, y = 14
At x = 8, y = 20
The slope of the line will be -
m = (20 - 14)/(8 - 4)
m = 6/4
m = 3/2
The general equation can be written as -
y = 3x/2 + c
20 = 3/2 x 8 + c
20 = 12 + c
c = 8
Now, we can write the equation as -
y = 1.5x + 8
Therefore, the equation that models the number of pages (y) and number of minutes (x) is y = 1.5x + 8.
To solve more questions on Equation modelling, visit the link below-
https://brainly.com/question/17928312
#SPJ2
4. Meg uses 1/2 of her supply of raisins
to make trail
mix and 3/10 of her supply of raisins to make
cookies. If Meg uses 8 pounds of raisins, how many
pounds of raising are in her supply
Answers
Answer:
10 pounds
Step-by-step explanation:
Let x represent the amount of raisins Meg have in her supply. She uses 1/2 of her supply of raisins to make trail mix and 3/10 of her supply of raisins to make cookies which gives a total of 8 pounds of raisins being used. To find the amount of raisins she has in her supply, we use the equation:
(1/2)x + (3/10)x = 8
multiply through by 20:
(1/2)x * 20 + (3/10)x * 20 = 8 * 20
10x + 6x = 160
16x = 160
Divide both sides of the equation by 16:
16x/16 = 160/16
x = 10 pounds
Therefore she have 10 pounds of raisins in her supply
The temperature was 8°F. It dropped so that the temperature was 0°F.
Answers
Answer:
It dropped 8 degrees so the answer must be -8
Step-by-step explanation:
My dad left to get milk and never came back!! when will he come back?
Answers
First, you would estimate how much milk your dad left to get. (1 gallon)
Second, you only have one dad, so put him in the equation.
Third, you will subtract dad from milk.
Lastly, your answer is 0. Therefore, your dad will never come back. Congratulations and I hope this helped!
Answer:
yes he will come back eventually just wait or you can goo look for him
14. (10.0 points) Given f(x)=sin(2πx), when x = 0.3, f(x) = 0.951057. Approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1. (Write your answer to 6 decimal points).
Answers
Given the function f(x)=sin(2πx), with x = 0.3, f(x) = 0.951057. The objective is to approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1.
We know that the Taylor series for a function f(x) can be written as:f(x)=f(a)+f′(a)(x−a)+f′′(a)2(x−a)2+…+f(n)(a)n!(x−a)n+…The first two terms of the Taylor series are given by:f(x)=f(a)+f′(a)(x−a)The first derivative of f(x) is given by:f′(x)=2πcos(2πx)On substituting x = a = 0.1, we get:f′(0.1) = 2πcos(2π * 0.1) = 5.03118603447The value of f(x) at a=0.1 is given by:f(0.1) = sin(2π * 0.1) = 0.587785252292With a=0.1, the first two terms of the Taylor series become:f(x)=0.587785252292+5.03118603447(x−0.1) = 0.587785252292+0.503118603447x−0.503118603447×0.1Using x=0.2 and substituting the values of a and f(a) in the equation above, we get:f(0.2)=0.587785252292+0.503118603447*0.2−0.503118603447×0.1=0.712261After approximating the value of f(0.2) using the first two terms in the Taylor series,
we can conclude that the value of f(0.2) = 0.712261 with a = 0.1, with an error of approximately 0.012796.
To know more about Taylor series visit
https://brainly.com/question/32235538
#SPJ11