13 over 11 equals 4 over u
Answers
Answer:
u = 44/13
Step-by-step explanation:
Step 1. Cross multiply
Step 2. Simplify each side
Step 3. Isolate variable
\(\frac{13}{11} =\frac{4}{u}\)
\(13u=(4)(11)\)
\(13u=44\)
\(u=44/13\)
BRAINLIEST please if this helped!Related Questions
let's see who can solve this. pleseeee

Answers
The correlation coefficient between X and Y is Corr(X, Y) = 0.
To calculate the marginal distribution of X and Y, we need to integrate the joint probability density function (PDF) over the appropriate ranges.
a. Marginal distribution of X:
To find the marginal distribution of X, we integrate the joint PDF over the range of Y:
∫[0, 1] J(x, y) dy
Since the joint PDF is defined as J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1 and J(x, y) = 0 otherwise, the integral becomes:
∫[0, x] 1 dy = x, for 0 ≤ x ≤ 1
So, the marginal distribution of X is simply X(x) = x for 0 ≤ x ≤ 1.
b. Expectation of X:
The expectation (mean) of X can be calculated as the integral of x times the marginal PDF of X:
\(E(X) = ∫[0, 1] x * X(x) dx = ∫[0, 1] x^2 dx = [x^3/3] from 0 to 1 = 1/3\)
Therefore, the expectation of X is E(X) = 1/3.
c. Variance of X:
The variance of X can be calculated using the formula:
\(Var(X) = E(X^2) - (E(X))^2E(X^2) = ∫[0, 1] x^2 * X(x) dx = ∫[0, 1] x^3 dx = [x^4/4] from 0 to 1 = 1/4Var(X) = 1/4 - (1/3)^2 = 1/4 - 1/9 = 5/36\)
Therefore, the variance of X is Var(X) = 5/36.
d. Covariance of X and Y:
The covariance of X and Y can be calculated as:
Cov(X, Y) = E(XY) - E(X)E(Y)
Since the joint PDF J(x, y) = 1 for 0 ≤ y ≤ x ≤ 1, the integral becomes:
\(E(XY) = ∫[0, 1] ∫[0, x] xy dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
\(E(X) = 1/3 (from part b)E(Y) = ∫[0, 1] ∫[0, x] y J(x, y) dy dx = ∫[0, 1] [(x^2)/2] dx = [(x^3)/6] from 0 to 1 = 1/6\)
Cov(X, Y) = 1/6 - (1/3)(1/6) = 0
Therefore, the covariance of X and Y is Cov(X, Y) = 0.
e. Correlation coefficient between X and Y:
The correlation coefficient can be calculated using the formula:
Corr(X, Y) = Cov(X, Y) / √(Var(X) * Var(Y))
Since the covariance of X and Y is 0, the correlation coefficient will also be 0.
Therefore, the correlation coefficient between X and Y is Corr(X, Y) = 0.
f. Conclusion based on the correlation coefficient:
The correlation coefficient of 0 indicates that there is no linear relationship between X and Y. In this case, the fraction of male runners (X) and the
for more such question on correlation visit
https://brainly.com/question/13879362
#SPJ8
Solve the equation below:
X-4 = -8.3 x=
Answers
Answer:
-4.3
Step-by-step explanation:
Add 4 to both sides and x = -4.3
Answer: x=-4.3
Step-by-step explanation:
x−4+4=−8.3+4
x=−4.3
A certain type of kickboard scooter comes in silver, red, 2
or purple with wheel sizes of 125 millimeters or 180
millimeters. Determine the total number of color-wheel size combinations.
(This is probability and I’m having such a hell of a time figuring it out pls help)
Answers
There are a total of 8 color-wheel size combinations for the kickboard scooter. This means that customers have 8 different options to choose from when selecting the color and wheel size for their scooter.
To determine the total number of color-wheel size combinations for the kickboard scooter, we need to multiply the number of color options by the number of wheel size options.
Given that there are 4 color options (silver, red, blue, and purple) and 2 wheel size options (125mm and 180mm), we can use the multiplication principle to find the total number of combinations:
Total combinations = Number of color options × Number of wheel size options
Total combinations = 4 colors × 2 wheel sizes
Total combinations = 8
There are a total of 8 color-wheel size combinations for the kickboard scooter. This means that customers have 8 different options to choose from when selecting the color and wheel size for their scooter.
For more such questions on combinations
https://brainly.com/question/28065038
#SPJ8
What is the standard form of y –7 = – 23 (x + 1)
Answers
Answer:
23x+y=-16
Step-by-step explanation:
Solve. 4x =16
I'm assuming solve for X but ^ that is all the question says

Answers
Answer:
x = 4
Step-by-step explanation:
4x = 16
divide both sides by 4:
⇒ \(\frac{4x}{4} = \frac{16}{4}\)
⇒ x = 4
Answer:
A. x = 4Step-by-step explanation:
4x = 16
x = 16 / 4
x = 4
Hope that helps!
What type of angles are 5 and 4
Answers
Answer:
show us a pic of the triangles
Step-by-step explanation:
Answer:
repost no pic
Step-by-step explanation:
Did i do this right?

Answers
Answer:
yes
Step-by-step explanation:
Jada went to the mall yesterday with $30.
• She spent 2/5 of her money on a new purse.
She spent / of what was left at the food court.
• She gave $5 to her friend.
How much did she have left?
Answers
are the side lengths of triangle Graph shows a triangle plotted on a coordinate plane. The triangle is at A(minus 7, 3), B(minus 3, 6), and C(5, 0). Type the correct answer in each box. If necessary, round any decimal to the nearest tenth. units units units
Answers
The side lengths for the triangle are given as follows:
AC = 12.4.AB = 5.BC = 10.How to calculate the distance between two points?Suppose that we have two points of the coordinate plane, and the ordered pairs have coordinates \((x_1,y_1)\) and \((x_2,y_2)\).
The shortest distance between them is given by the equation presented as follows, derived from the Pythagorean Theorem:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Then the length AC is given as follows:
\(AC = \sqrt{(5 - (-7))^2 + (0 - 3)^2}\)
AC = 12.4.
The length AB is given as follows:
\(AB = \sqrt{(-3 - (-7))^2 + (6 - 3)^2}\)
AB = 5.
The length BC is given as follows:
\(BC = \sqrt{(5 - (-3))^2 + (6 - 0)^2}\)
BC = 10.
More can be learned about the distance between two points at https://brainly.com/question/7243416
#SPJ1
Mark wants to be a chef someday and would like to start learning to grow his own
ingredients in a garden. His mom gives him 12 square feet of space in the back yard to plant
a garden. He marks off % of it to save for a tomato plant and has the rest to use for onions.
Each onion bulb needs square feet of room to grow. How many onion bulbs can he
plant?
Answers
The area of the space available for onions is:n12 square feet - 0.12x square feet. number of onion bulbs Mark can plant is: (12 - 0.12x) / y
What is percentage?
Percentage is a way of expressing a number or proportion as a fraction of 100. It is represented by the symbol "%".
Mark has marked off a certain percentage of the 12 square feet to save for a tomato plant, which means the remaining space will be used for onions.
Let's say Mark marks off x% of the space for the tomato plant. That means he will have (100-x)% of the space for onions.
The area of the space reserved for the tomato plant is:
12 square feet x (x/100) = 0.12x square feet
The area of the space available for onions is:
12 square feet - 0.12x square feet
Let's say each onion bulb needs y square feet of room to grow. Mark can plant as many onion bulbs as can fit in the remaining space, which is:
(12 square feet - 0.12x square feet) / y
So the number of onion bulbs Mark can plant is:
(12 - 0.12x) / y.
To learn more about percentage from the given link:
https://brainly.com/question/29306119
#SPJ1
The function
f(x) = 5sqrt(x + 13) + 5 has an inverse f ^ - 1 * (x) defined on the domain x < 5 Find the inverse. x >= - 13
Answers
The inverse function: \(f^{-1} (x) =\) \((\frac{x -5}{5} )^{2} -13\)
The inverse is defined on the domain x < 5 and x ≥ -13 for the original function, which means that the range of the original function is y ≥ 5.
What is a function?A function is a relationship that exists between two sets of numbers, with each input from the first set, known as the domain, corresponding to only one output from the second set, known as the range.
Given function is; \(f(x) = 5\sqrt{(x + 13)} + 5\)
To find the inverse of the given function, we first replace f(x) with y:
⇒ \(y = 5\sqrt{(x + 13)} + 5\)
Subtract 5 from both sides:
⇒ \(y -5 = 5\sqrt{(x + 13)}\)
⇒ \(\frac{(y -5)}{5} = \sqrt{(x + 13)}\)
⇒ \((\frac{y -5}{5} )^{2} = x + 13\)
⇒ \((\frac{y -5}{5} )^{2} -13 = x\)
Now we have x in terms of y, so we can replace x with f⁻¹(x) and y with x to get the inverse function:
f⁻¹(x) = \((\frac{x -5}{5} )^{2} -13\)
The domain of the inverse function is x ≥ 5, because this is the range of the original function, and we were given that the inverse is defined on the domain x < 5. However, we must also exclude the value x = 5, because the denominator of the fraction \((\frac{x -5}{5} )^{2}\) becomes zero at this value. Therefore, the domain of f⁻¹(x) is x > 5.
We were given that x ≥ -13 for the original function, which means that the range of the original function is y ≥ 5. Therefore, the domain of the inverse function becomes the range of the original function, and the range of the inverse function becomes the domain of the original function.
To know more about domain, visit:
https://brainly.com/question/26098895
#SPJ1
The head of maintenance at XYZ Rent-A-Car believes that the mean number of miles between services is 2135 miles, with a variance of 145,924. If he is correct, what is the probability that the mean of a sample of 40 cars would differ from the population mean by less than 29 miles
Answers
Answer:
0.36878
Step-by-step explanation:
Given that:
Mean number of miles (m) = 2135 miles
Variance = 145924
Sample size (n) = 40
Standard deviation (s) = √variance = √145924 = 382
probability that the mean of a sample of 40 cars would differ from the population mean by less than 29 miles
P( 2135 - 29 < z < 2135 + 29)
Z = (x - m) / s /√n
Z = [(2106 - 2135) / 382 / √40] < z < [(2164 - 2135) / 382 / √40]
Z = (- 29 / 60.399503) < z < (29 / 60.399503)
Z = - 0.4801364 < z < 0.4801364
P(Z < - 0.48) = 0.31561
P(Z < - 0.48) = 0.68439
P(- 0.480 < z < 0.480) = 0.68439 - 0.31561 = 0.36878
= 0.36878
Answer: 0.3688
Step-by-step explanation:
If you are rounding to the nearest 4 decimal places the correct answer is 0.3688
What is the length of EF in the right triangle below?
D
26
10
E
F
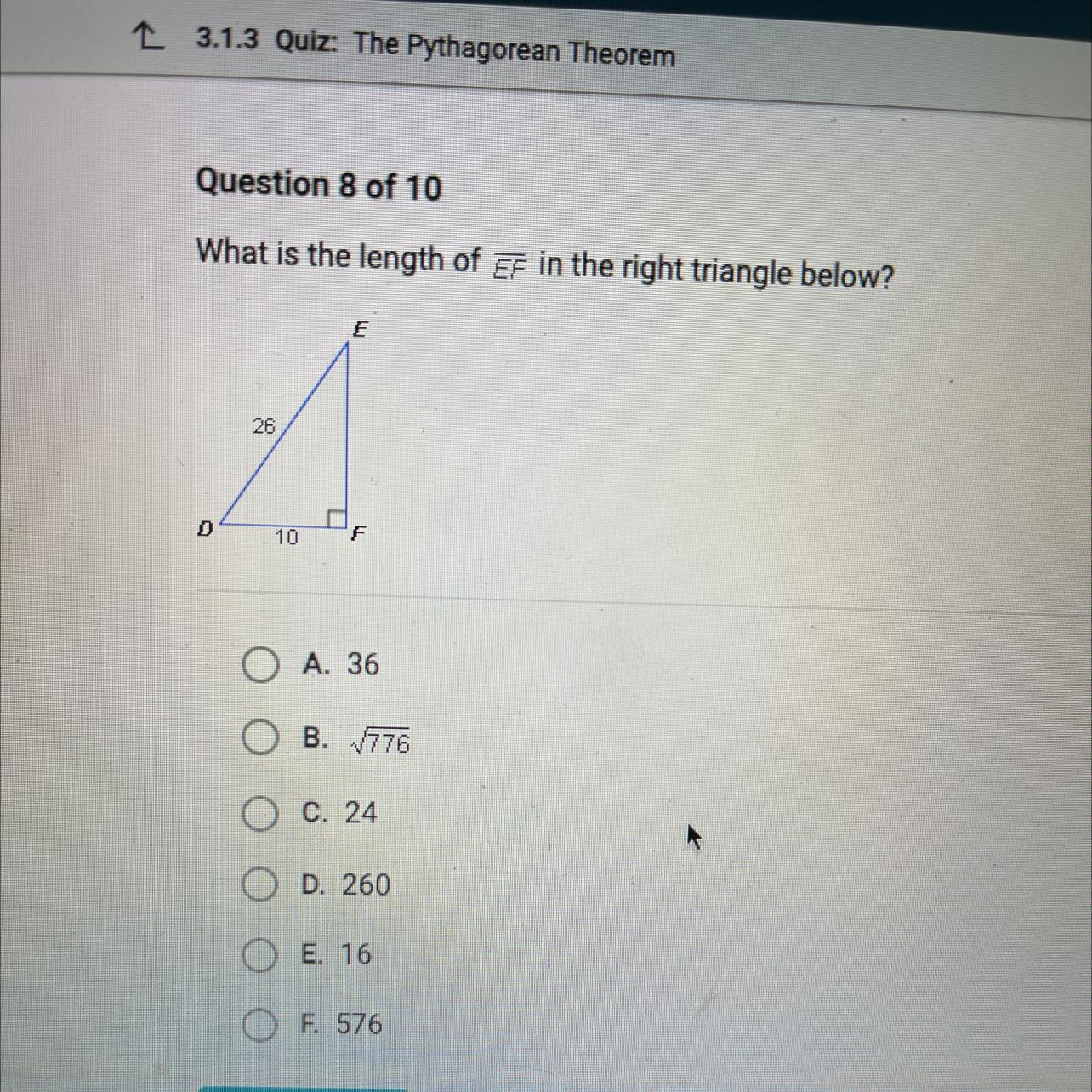
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
On a trip, you had to change your money from dollars to British pounds.
You got 560 pounds for 800 dollars.
Which is a unit rate that describes the exchange?
135 pounds per dollar
0.625 pounds per dollar
137 pounds per dollar
0.7 pound per dollar
Answers
Answer:
0.7 pound per dollar
Step-by-step explanation:
To find the pounds per dollar, divide the number of pounds by the number of dollars:
560/800
= 0.7
So, the unit rate is 0.7 pounds per dollar
I need the answer. Please help.

Answers
Answer:
300°
Step-by-step explanation:
To convert from radians to degrees
degree = radian × \(\frac{180}{\pi }\) , then
degree = \(\frac{5\pi }{3}\) × \(\frac{180}{\pi }\) ( cancel π on numerator/ denominator )
= \(\frac{5(180)}{3}\)
= 5 × 60°
= 300°
Calcular los 3/5 de los 2/3 de las 3/4 de 560
Answers
For the fractions, the calculation of 3/5 of 2/3 of 3/4 of 560 is equal to 168.
How to solve fractions?To calculate 3/5 of 2/3 of 3/4 of 560, break it down step by step:
Step 1: Calculate 3/4 of 560:
3/4 × 560 = (3 × 560) / 4 = 1680 / 4 = 420
Step 2: Calculate 2/3 of the result from Step 1:
2/3 × 420 = (2 × 420) / 3 = 840 / 3 = 280
Step 3: Calculate 3/5 of the result from Step 2:
3/5 × 280 = (3 × 280) / 5 = 840 / 5 = 168
Therefore, 3/5 of 2/3 of 3/4 of 560 is equal to 168.
Find out more on fractions here: https://brainly.com/question/78672
#SPJ1
3.6 units
A.
(-3, 4) and (3,4)
4.5 units
B.
(-5,3) and (-5, 11)
6 units
C.
(-20, -18) and (-22, -21)
8 units
D.
(-2, 4) and origin
15 units
E.
(7.-8) and (-2,-20)
Which of the following is correct sequence of the matching?
Answers
Answer:
Answer: A = 6 units, B = 8 units, C = 3.6 units, D = 4.5 units, E = 15 units
Step-by-step explanation:
A and B can be solved by inspection, as they have a co-ordinate that is the same: A (-3;4) and (3;4) has the same y-coordinate, so the distance between the points can be measured by the difference in their x-coordinates; B (-5;3) and (-5;11) has the same x-coordinates, so the distance can be measured by the difference in their y-coordinates.
which expression is equivalent to g^2/3h
Answers
The given expression \(g^2/3h\) is equivalent to the option (c) \(8g^2/24h\)as we have multiplied 8 in both numerator and denominator.
The given expression is \(g^2/3h\).
Now, to further simplify the expression, we can multiply both numerator and denominator by 8. This gives us:
\((g^2/3h) * (8/8)\)
Simplifying further, we get:
\((8g^2)/(24h)\)
Therefore, the expression equivalent to \(g^2/3h\) is \((8g^2)/(24h)\).
Thus, the given expression \(g^2/3h\) is equivalent to the option (c) \(8g^2/24h\) as we have multiplied 8 in both numerator and denominator.
The numerator is the top part of a fraction, which represents the number of equal parts being considered. It is the value that is above the fraction bar and represents the quantity being divided into equal parts.
Learn more about denominator :
https://brainly.com/question/7067665
#SPJ1
The complete question is :
Which expression is equivalent to \(g^2/3h\)?
Click on the correct answer.
(A) \(g^2+5/3h+5\)
(B) \(6g^2/15h\)
(C) \(8g^2/24h\)
The distance from Ellen's home to her school is 4 miles. If she has already traveled 2 miles, how far does she have to go?
Answers
Answer:
6 miles
Step-by-step explanation:
10. A boxer was able to land 10 punches in 4 rounds. At this rate, how many punches
would he land in 9 rounds? If you get stuck, consider using the table.
punches
round
10
4
1
9
Answers
Answer:
22.5 punches in 9 rounds.
Step-by-step explanation:
To find the number of punches in 1 round, you divide 4 by 4 and 10 by 4. 4 divided by 4 is 1. 10 divided by 4 is 2.5. Next, multiply 1 by 9 to get 9. Then multiply 2.5 by 9 to get 22.5
So, a boxer can land 22.5 punches in 9 rounds. If you need to round, it would be 23 punches in 9 rounds.
Hope this helps!
what is the best estimate for the product 9/10 x 5/11
Answers
The best estimate for the product 9/10 x 5/11 is 1/2.
What is product?Product in Mathematics simply means a number that you get when you multiply. It is used to illustrate tye concept of multiplication
In this case, the estimate for 9/10 is 1 and the estimate of 5/11 is 1/2. Therefore, the product will be:
= 1 × 1/2
= 1/2
This shows the estimation.
Learn more about product on:
brainly.com/question/25301924
#SPJ1
what property is occurring in the following example? 11.5 + (- 11.5) = 0
A- Commutative
B- Associative
C- Addictive Inverse
D- Distributive Property
PLEASE I NEED ANSWERS!!
Answers
Answer: A property occurring in the example 11.5 + (-11.5) = 0, is additive inverse.
Step-by-step explanation:
A property where sum of any number and its inverse is equal to zero is called additive inverse property.
For example, 11.5 + (-11.5) = 0
Here, 11.5 is the number and its inverse is (-11.5). The sum of both these is equal to zero. Hence, it shows a property of additive inverse.
Thus, we can conclude that property occurring in the example 11.5 + (-11.5) = 0, is additive inverse.
work out m and c for the line y= 2x+1
Answers
Answer:
m = 2, c = 1
Explanation: In the y = mx + b (or y = mx + c) format, the m is the slope of the line and the c/b is the y-intercept, or where the line crosses the y-axis. If we substitute the information from the given equation, y = 2x + 1, into the general formula, we know that the m is 2 and c is 1.
A game card handed out at a grocery store states the probabilities of winning a prize: 0.2 for $10, 0.1 for $5, and 0.7 for $0. What is the probability of winning any amount of money?
Answers
Answer:
Step-by-step explanation:
To calculate the probability of winning any amount of money, we need to sum up the probabilities of winning each individual prize.
Given the probabilities stated on the game card:
Probability of winning $10 prize = 0.2
Probability of winning $5 prize = 0.1
Probability of winning $0 prize = 0.7
To find the probability of winning any amount of money, we add these probabilities together:
0.2 + 0.1 + 0.7 = 1
The sum of the probabilities is 1, which indicates that the total probability of winning any amount of money is 1 or 100%.
Therefore, the probability of winning any amount of money in this game is 100%.
Hope this answer your question
Please rate the answer and
mark me ask Brainliest it helps a lot
Solve for x.
5x – 31 = 23 - X
x = [?]
Answers
Answer:
X=9
Step-by-step explanation:
Have a good day!
![Solve for x.5x 31 = 23 - Xx = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/fVYwOdX3pPOZvrvQd1wWB14OW1F0kitl.png)
Copy and complete the table of values for
y = -2x² + 4x + 9.
What numbers replace A and B?

Answers
Answer:
Below in bold.
Step-by-step explanation:
A = value of y when x = -1:
A = -2(-1)^2 + 4(-1) + 9
= -2*1 - 4 + 9
= -2 - 4 + 9
= 3.
B = value of y when x = 2:
B = -2(2)^2 + 4(2) + 9
= -2*4 + 8 + 9
= - 8 + 8 + 9
= 9.
Please please help please help me help help me please help me

Answers
Answer:
\(m = \frac{6 - 5}{4 - 1} \\ \color{green} \boxed{m = \frac{1}{3} }\)
A jar holds blue and green marbles. There are 57 blue marbles in the jar. There are 23 fewer green marbles than blue marbles in the jar.how many green marbles are there in the jar? How many marbles are there in altogether?
Answers
Answer:
there are 34 green marbles
there are 91 total marbles
Step-by-step explanation:
57 - 23 = 34
57 + 34 = 91
3
a)
b)
c)
Elana wants to use her grandmother's old biscuit recipe:
BISCUIT RECIPE
INGREDIENTS
1 cups flour
cup suger
2 tsp baking powder
tsp salt
cup cream
METHOD
Preheat the oven to 350 F
Mix all the ingredients.
Roll the dough into 7
Place on baking tray, 1 inch apart.
Bake for 20 minutes.
inch rounds.
Elana must roll the dough into 7
Convert the measurement to cm.
Rewrite all the ingredients using either grams or millilitres.
What temperature should Elana heat the oven to?
Write your answer in °C.
inch rounds.
OUMA'S
BAKING
RECIPES
d)
How far apart should the biscuits be on the baking tray?
Write your answer in cm.
Mandisa is going to the United States of America.
This is her itinerary:
Nihal bakes a pie. The recipe says the oven must be set at 450 °F.
What is the temperature in °C?
Was
Today
Sep 21
ST
67 °F
75 °F
Disney Wo
Today
Sep 21
IT
76 °F
91 °F
Califor
Toda
Sep
Answers
The biscuits should be placed 2.54 centimeters apart on the baking tray.
What is the unitary method?
The unitary method is a way for solving a problem by the first value of a single unit and than finding the value by multiplying the single unit. Unitary method is a technique by which we can find the value of a single value from the value of more than one devices and the value of more than one unit from the value of a single unit. We can this method use for most of the calculations in math.
We are given that;
Elana must roll the dough into 7 inch rounds.
a) To convert this measurement to centimeters, we can use the conversion factor 1 inch = 2.54 centimeters. Therefore, 7 inches is equal to:
7 inches x 2.54 centimeters/inch = 17.78 centimeters
So, Elana must roll the dough into 17.78 centimeter rounds.
b) To rewrite all the ingredients using grams or milliliters, we need to know the density of each ingredient. Assuming that the density of each ingredient is the same as that of all-purpose flour (which is approximately 125 grams per cup), we can convert the measurements as follows:
1 cup flour = 125 grams flour
1/2 cup sugar = 100 grams sugar
2 teaspoons baking powder = 10 grams baking powder
1 teaspoon salt = 5 grams salt
1/2 cup cream = 120 milliliters cream (assuming a density of 1 gram per milliliter)
So, the rewritten ingredients are:
125 grams flour
100 grams sugar
10 grams baking powder
5 grams salt
120 milliliters cream
c) The recipe states that the oven should be preheated to 350 °F. To convert this temperature to Celsius, we can use the formula:
Celsius = (Fahrenheit - 32) x 5/9
So, the temperature in Celsius is:
Celsius = (350 - 32) x 5/9 = 176.67 °C
Therefore, Elana should heat the oven to 176.67 °C.
d) The recipe states that the biscuits should be placed on the baking tray 1 inch apart. To convert this measurement to centimeters, we can use the conversion factor 1 inch = 2.54 centimeters. Therefore, the biscuits should be placed on the baking tray:
1 inch x 2.54 centimeters/inch = 2.54 centimeters
Therefore, by unitary method answer will be 2.54 centimeters.
To learn more about the unitary method, visit;
https://brainly.com/question/23423168
#SPJ9
Expression equivalent to 8p-3n+4q-9m
Answers
Answer:
4p-n+2q-3m is equivalent to 8p-3n+4q-9m
The expression 4(2p+ q) - 3(n+3m) is equivalent to the given expression. which is the correct answer would be an option (C).
What is the expression?Expressions are defined as mathematical statements that have a minimum of two terms containing variables or numbers.
The expression is given in the question following:
8p - 3n + 4q - 9m
We have to determine the equivalent expression to the given expression
As per option (C), we have
⇒ 4(2p+ q) - 3(n+3m)
Apply the distributive property of multiplication,
⇒ 4 × 2p+ 4 × q - 3 × n + 3 × m
⇒ 8p + 4q - 3n + 3m
Rearrange the terms in the above expression,
⇒ 8p - 3n + 4q - 9m
So this expression is the same as the given expression.
Therefore, the expression 4(2p+ q) - 3(n+3m) is equivalent to the given expression.
Learn more about Expressions here :
brainly.com/question/21751419
#SPJ5
The question seems to be incomplete the correct question would be:
Which expression is equivalent to 8p-3n+4q-9m
A. 0
B. 5pn - 5qm
C. 4(2p+ q)-3(n+3m)
D. 4(2p+q)-3(n-3m)