Answers
Answer:
0Step-by-step explanation:
Solving in steps
3| 4.5 - 2| - 5 |-1.5 -(- 3)| =3 |2.5| -5 |-1.5 + 3| =3*2.5 - 5|1.5| =7.5 - 5*1.5 =7.5 - 7.5=0Related Questions
Declan said, "I know 3/4 is greater than 1/2, so that means 3/4 is greater than 6/12. " Does Declan’s reasoning make sense?
Answers
Declan's reasoning does make sense. This is because 3/4 and 1/2 have the same denominator, and 3/4 is a larger fraction than 1/2.
Therefore, it is reasonable to assume that 3/4 is greater than 6/12 because 6/12 simplifies to 1/2. Simplifying fractions means dividing the numerator and denominator by the same number, in this case, 6 is divisible by 2, so we can reduce the fraction to 1/2.
So, Declan is correct in his reasoning that 3/4 is greater than 6/12. It is important to understand the relationship between fractions and their denominators to make such comparisons accurately.
3/4 = 9/12
1/2 = 6/12
6/12 = 6/12
Since 9/12 (which is equivalent to 3/4) is greater than 6/12 (which is equivalent to 1/2), we can say that 3/4 is indeed greater than 6/12.
Therefore, Declan's reasoning is correct.
Learn more about Fractions:
https://brainly.com/question/78672
#SPJ4
A man drove 14 mi directly east from his home, made a left turn at an intersection, and then traveled 9 mi north to his place of work. if a road was made directly from his home to his place of work, what would its distance be to the nearest tenth of a mile?
Answers
If a road was made directly from his home to his place of work, its distance will be 16.6 mi.
If a man drives east from his home, makes a left turn at an intersection, and then travels north to his place of work, then the path he travels resembles the sides of a right triangle (see attached photo).
if a road was made directly from his home to his place of work, then this path will be the hypotenuse of the triangular path.
Using Pythagorean theorem, we can solve for the distance of the road.
c^2 = a^2 + b^2
where c is the distance of the road
a is the distance he travels to the east
b is the distance he travels up north
c^2 = a^2 + b^2
c^2 = (14 mi)^2 + (9 mi)^2
c^2 = (196 + 81) mi^2
c^2 = 277 mi^2
c = 16.64331698 mi
distance of the road = c = 16.64331698 mi
Rounding off to the nearest tenth of a mile:
distance of the road = 16.6 mi
Learn more about Pythagorean Theorem here: https://brainly.com/question/343682
#SPJ4

A bag contains 4 Snickers bars and 1 Twix bar, and the outcome is drawing a Twix bar. Does the phrase that describes the probability of drawing a Twix bar
A.
No, because there are still only two possible outcomes.
B.
No, because it is still less likely to have an outcome of drawing a Twix.
C.
Yes, because there are still only two possible outcomes.
D.
Yes, because it is still less likely to have an outcome of drawing a Twix.
Answers
Answer:
Yes because there are still only two possible outcomes
Step-by-step explanation:
I think it’s this one cause I’m on it too
si tenemos una pantalla de television, cuyos lados mide 2x+4 y 5x+5, cuales el perimetro de la pantalla?
Answers
Answer:
P=14x+18
Step-by-step explanation:
perimeter:
P=2(2x+4)+2(5x+5)=4x+8+10x+10=14x+18
I hope this help you
What is the area of the rooftop garden?

Answers
The area of the rooftop garden as required in the task content is; 272 ft².
What is the area of the rooftop garden?It follows from the task content that the area of the rooftop garden is to be determined.
As evident in the attached image; the rooftop garden was modelled as a composite figure of a rectangle and a triangle.
Therefore, the area of the rooftop garden is the sum of areas of the rectangle and the triangle.
Where the heights of the triangle is; 20 - 12 = 8 ft.
Therefore, we have;
Area = { (1/2) × 8 × 8 } + { 12 × 20}
Area = 32 + 240
Area = 272 ft².
Ultimately, the required area of the rooftop garden is; 272 ft².
Read more on area of Triangles;
https://brainly.com/question/17335144
#SPJ1
WILL GIVE BRAINLY PLEASEEEEEEEE RIGHT NOW ANSWER What is the greatest common factor of 20 and 36?
O 2
O 4
O5
O 6
Answers
Answer:
4
Step-by-step explanation:
Answer: 4
Step-by-step explanation:
It can't be 6 or 5 because 20 isn't divisible by 6 and 36 isn't divisible by 5
Leslie says 2/11 + 3/4 = 5/15. What mistake has Leslie made?
Answers
Answer:
Leslie did not find the common denominator of the fractions before adding them.
Step-by-step explanation:
Correct way:
\(\frac{2}{11} + \frac{3}{4} = \frac{8}{44} + \frac{33}{44} = \frac{41}{44}\)
Need the answer to the problem below.
((4 * 10) ^ 10) ^ 10 =
Answers
Answer:
Here is your answer
((4 * 10) ^ 10) ^ 10 =
(40 ^ 10) ^ 10 =
10485760000000000 ^ 10 = 16069380442589902755419620923411626025222029937827928353013760000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Step-by-step explanation:
You ask Vince to determine the distance the brake anchor has to be placed away from the base of the ending tree so the brake will just reach the tree.
• Vince measures 24 feet away from the base of the tree because the bungee cord is 24 feet long.
• He adds 18 extra feet, to allow the bungee cord to stretch to capacity.
• Vince places the brake anchor 42 feet from the base of the ending tree
Vince's anchor is not at the correct distance from the tree. • What is the flaw in Vince's process? • Find the distance the brake anchor should be placed away from the base of the tree so the brake will just reach the tree. • Explain to Vince how you found the distance. Justify your reasoning mathematically.
Answers
The correct distance for placing the brake anchor is 6 feet away from the base of the tree.
Let's break down the information given:
Vince measured 24 feet away from the base of the tree because the bungee cord is 24 feet long.
He added 18 extra feet to allow the bungee cord to stretch to capacity.
Vince placed the brake anchor 42 feet from the base of the ending tree.
The flaw in Vince's process lies in his failure to account for the additional stretch of the bungee cord. By placing the brake anchor at 42 feet, he did not consider the extended length the bungee cord would reach.
To find the correct distance, we need to subtract the total length of the bungee cord, including the additional stretch, from the distance Vince measured. Let's calculate this step by step:
Total length of the bungee cord, including extra stretch:
24 feet (length of the bungee cord) + 18 feet (extra stretch) = 42 feet
Distance the brake anchor should be placed away from the base of the tree:
24 feet (Vince's measurement) - 42 feet (total length of the bungee cord) = -18 feet
The negative result indicates that Vince's anchor should be placed 18 feet closer to the base of the tree than his initial measurement. This means
=> (24 feet - 18 feet) = 6 feet.
To know more about distance here
https://brainly.com/question/4199102
#SPJ4
At the beginning of a baking session, there were 2.26 kilograms of flour in the bag. By the end of the baking session, there was 0.98 kilogram of flour in the bag. What is the percent of decrease in the amount of flour? Round the percent to the nearest tenth if necessary.
Answers
Answer:
The answer I got was 56.6%.
Let f(x) = -5x + 6. Find and simplify f(p). f(p) = (Simplify your answer.)
Answers
To find and simplify f(p), where f(x) = -5x + 6, we substitute the variable p into the function and evaluate it. The simplified expression for f(p) is -5p + 6.
In this case, the function f(x) is given as -5x + 6. To find f(p), we substitute p in place of x in the function. Substituting p into the expression, we get -5p + 6. Thus, the simplified form of f(p) is -5p + 6.
The function f(x) represents a linear equation with a slope of -5 and a y-intercept of 6. When we substitute p for x, we essentially evaluate the function at the value p. The result, -5p + 6, gives us the value of f(p) for the given value of p. The expression -5p + 6 represents the linear equation with the same slope and y-intercept as the original function, but evaluated at the specific value of p. This means that if we substitute any value of p into f(p), the result will be -5 times that value plus 6.
Learn more about linear equation here: brainly.com/question/32634451
#SPJ11
How do you use the binomial theorem to expand the expression (x + y)^4?
Answers
We establish the given binomial expression (x + y)^4 in the following way
What is binomial theorem in simple terms?The nth power of the sum of two integers a and b may be represented as the sum of n + 1 terms of the form, according to the binomial theorem, which states that for every positive integer n.
What is a binomial equation in math?A polynomial with just terms is a binomial. An illustration of a binomial is x + 2, where x and 2 are two distinct words. Additionally, in this case, x has a coefficient of 1, an exponent of 1, and a constant of 2. As a result, a binomial is a two-term algebraic statement that comprises a constant, exponents, a variable, and a coefficient.
(x+y) 4=
((x+y)2) 2=
(x2+2xy+y2) 2=
(x2+2xy) 2+2(x2+2xy) (y2)+(y2) 2=
(x4+4x3y+4x2y2)+(2x2y2+4xy3)+(y4)=
x4+4x3y+6x2y2+4xy3+y4
The binomal theorem is a more comprehensive strategy:
(x+y)
n=∑k=0n(nk)
⋅xn−k⋅yk=∑k=0n(nk)
⋅xk⋅yn−k\sWhere\s(nk)=n!((n−k)!)⋅(k!)
n!={1n⋅((n−1)!)
n=0n>0
∑k=0nf(k)=f(0)+f(1)+f(2)+…+f(n)
To learn more about binomial theorem, click the following link:-
https://brainly.com/question/13672615
#SPJ1
Between 11 P.M. and 8:54 A.M., the water level in a swimming pool decreased by 11/20. Assuming that the water level decreased at a constant rate, how much did the water level drop each hour?
Answers
Answer:
The water level decreased by 1/18 inches each hour.
Step-by-step explanation:
A rate of change is a rate that describes how one quantity changes in relation to another quantity. Between 11 P.M. and 8:54 A.M., the water level in a swimming pool decreased by 11/20, for each hour it decreases by 33/554
What is Rate of change?A rate of change is a rate that describes how one quantity changes in relation to another quantity.
Given that, Between 11 P.M. and 8:54 A.M., the water level in a swimming pool decreased by 11/20. Assuming that the water level decreased at a constant rate, we need to find the amount of water level drop each hour.
In an hour we will have sixty minutes.
We need to calculate the number of minutes between 11 pm and 8: 54 am.
The minutes between 11 P.M. and 8:54 A.M. is 594 minutes.
So in 554 min water level drop is 11/20.
So in 1 min=11/20×1/554
So in 60 min
We need to multiply with sixty
= 60(11/20×1/554)
We need to solve 60(11/20×1/554), we get
=3(11/554)
3 times of eleven by five hundred fifty four.
=33/554
Hence 33/554 water level drop each hour when water level decreased at a constant rate.
To learn more on Rate of change click:
https://brainly.com/question/12786410
#SPJ2
Consider the problem minimize f(x)=x_1^2+2x_2^2+3x_3^2 subject to x1+x2+x3≥1 x1≥0 x2≥0 x3≥0. Apply the simple active - set method to the problem, using initial guess x0=(5,9,2)^T. Compute a search direction using a reduced Newton method.
Answers
The updated solution is x1 = 5/2, x2 = 9/4, and x3 = 0.
To apply the Simple Active-Set Method to the given problem, we first write the Lagrangian function as:
L(x, λ) = x1^2 + 2x2^2 + 3x3^2 - λ(x1 + x2 + x3 - 1)
where λ is the Lagrange multiplier.
At each iteration, we need to identify the active set of constraints and solve a subproblem to find the search direction. We start with the initial guess x0 = (5, 9, 2)^T and assume that all constraints are inactive.
Step 1: Check Optimality
We calculate the gradient of the Lagrangian as:
∇L(x, λ) = [2x1 - λ, 4x2 - λ, 6x3 - λ, -(x1 + x2 + x3 - 1)]
Setting this gradient to zero, we get:
x1 = λ/2
x2 = λ/4
x3 = λ/6
x1 + x2 + x3 = 1
Substituting these values into the constraint inequalities, we get:
λ/2 ≥ 0
λ/4 ≥ 0
λ/6 ≥ 0
These conditions imply that λ ≥ 0. Since the objective function is strictly convex, the point x0 = (5, 9, 2)^T is not optimal.
Step 2: Identify Active Constraints
Since λ ≥ 0, the first two inequality constraints are inactive. The third inequality constraint is active, i.e., x3 = 0.
Substituting x3 = 0 into the objective function and the remaining constraints, we get:
minimize f(x) = x1^2 + 2x2^2
subject to x1 + x2 ≥ 1
x1 ≥ 0
x2 ≥ 0
The active-set subproblem is to minimize the above objective function subject to the given constraints.
Step 3: Solve Active-Set Subproblem
We use a reduced Newton method to solve the active-set subproblem. The reduced Hessian is given by:
H = [2 0]
[0 4]
At the current point x0 = (5, 9, 0)^T, we have:
∇f(x0) = [10, 36]^T
Solving the equation HΔx = -∇f(x0), we get:
Δx = [-5/2, -9/4]^T
Step 4: Update Solution
The search direction Δx is in the direction of decreasing f(x). However, we need to ensure that the constraints are satisfied after taking the step Δx. In particular, we need to check if any previously inactive constraints have become active or any previously active constraints have become inactive.
In this case, the only active constraint is x1 + x2 ≥ 1. We can take the full step Δx = [-5/2, -9/4]^T since it satisfies the constraint x1 + x2 ≥ 1.
Therefore, the updated solution is x1 = 5/2, x2 = 9/4, and x3 = 0.
Learn more about solution from
https://brainly.com/question/27894163
#SPJ11
In △ A B C , ∠ C is a right angle and sin A = 4 5 . What is the ratio of cos A?
Answers
The ratio of the trigonometric function of the right triangle, cos A is 3/5.
Given that,
In △ABC , ∠C is a right angle.
Then the opposite side to the right angle will be the hypotenuse.
So AB is the hypotenuse.
Sin A = BC / AB [ Since sine of an angle is opposite side / hypotenuse]
BC / AB = 4/5
BC = 4 and AB = 5
Using the Pythagoras theorem,
Third side, AC = √(5² - 4²) = 3
Cos of an angle is the ratio of adjacent side to the hypotenuse.
Cos A = 3/5
Alternatively, we can use the identity,
sin²A + cos²A = 1
to find the value of cos A.
Hence the value of cos A is 3/5.
Learn more about Trigonometric Functions here :
https://brainly.com/question/29269112
#SPJ1
how do i find the y intercept for 14x+y=140 and what would the slope be? and what would the x intercept be?
Answers
Answer:
y-intercept: 140slope: -14x-intercept: 10Step-by-step explanation:
You want to know the intercepts and slope of the line whose equation is ...
14x +y = 140
InterceptsEach intercept is the solution to the equation when the other variable is set to zero.
To find the y-intercept, use x=0: y = 140.
To find the x-intercept, use y=0: 14x = 140 ⇒ x = 10
SlopeThe slope is the coefficient of x when the equation is solved for y:
14x +y = 140
y = -14x +140 . . . . . the x-coefficient is -14
The y-intercept is 140; the slope is -14; the x-intercept is 10.
__
Additional comment
As you can see, when the equation is in standard form:
ax +by = c
The intercepts are ...
x-intercept = c/a
y-intercept = c/b
and the slope is ...
slope = -a/b
A lawyer has an annual income of $142,500. The income tax she has to pay is 15%. What is the amount of income tax in dollars and cents that the lawyer has to pay? PLZ help
Answers
Answer:
Im mad that you didnt helped me >:(
Date:
On
a
farm, there were a total of 440 goats, ducks and chickens.
The number of ducks
was
of the number of chickens. After 1/2 of the goats and of the 1/2 ducks were released, there was a total of 320 goats, ducks and chickens left. Find the number of goats
farm at first.
Answers
Answer:
Step-by-step explanation:
Because we have 3 unknowns, we need to come up with 3 equations. If the total number of animals is 440 and that number is made up of a combination of goats (g), ducks (d), and chickens (c) the first equation is
g + d + c = 440
The next equation is found in the fact that the number of ducks is one-quarter the number of chickens:
\(d=\frac{1}{4}c\) and solving for c gives us that
c = 4d
The last equation says that of the total number of animals, 440, half the goats and half the ducks got away, leaving only 320 animals behind. The last equation, the tricky one, is:
\(440-\frac{1}{2}g-\frac{1}{2}d=320\) and simplifying that:
\(-\frac{1}{2}g-\frac{1}{2}d=-120\) and because nobody hates fractions more than I do, I'm going to get rid of them by multiplying everything by 2 to get:
-g - d = -240
We've got these equations now, but what I'm going to do is to sub in what c equals (c = 4d) for c in the first equation:
g + d + 4d = 440 and
g + 5d = 440 and pair that with the one right above:
-g - 1d = -240 and use elimination to solve. The g's cancel each other out, leaving us with 4d = 200 and d = 50. So there were 50 ducks originally. Now we will sub that in to solve for c:
c = 4d so
c = 4(50) and
c = 200. Now we will sub both those values into the very first equation we put together to solve for g:
g + 200 + 50 = 440 and
g + 250 = 440 so
g = 190.
Add them all together just to be sure we have the 440 that we were told we had in the beginning (and we do, so we're all done!)
The blue segment below is a radius of oo. What is the length of the diameter
of the circle?
A. 4.9 units
B. 14.7 units
C. 9.8 units
D. 19.6 units

Answers
Answer:
D. 19.6 unitsStep-by-step explanation:
diameter = 2r
where r = 9.8
plugin value of r = 9.8 into the formula:
diameter = 2(9.8)
= 19.6 units
The length of the diameter of the circle is option D 19.6 units.
What is the diameter?Diameter is defined as the line from one point in the circle to the other point through the center of the circle.
WE know that the diameter = 2r
where r = 9.8
Substitute value of r = 9.8 into the formula:
The diameter = 2(9.8)
The diameter = 19.6 units
Hence, the length of the diameter of the circle is option D 19.6 units.
Learn more about circle here;
brainly.com/question/12512221
#SPJ2
ook at these three equations.
6(x−2)=6x−3
2(x−3)=2x−6
3(x−2)=x−6
Which of the equations has exactly one solution?
Answers
Answer:
third
Step-by-step explanation:
Answer:
3(x-2)=x-6 would be correct
(-9x² + 11x +2) x (8x² + 6x -7)
Answers
Answer:
-72x^4 + 34x^3 + 145x^2 - 65x - 14
Step-by-step explanation:
(-9x² + 11x +2) x (8x² + 6x -7)
= -72x^4 - 54x^3 + 63x^2 + 88x^3 + 66x^2 - 77x + 16x^2 + 12x - 14
= -72x^4 + 34x^3 + 145x^2 - 65x - 14
So, the answer is -72x^4 + 34x^3 + 145x^2 - 65x - 14
(-9x² + 11x + 2) x (8x² + 6x - 7)
= -9x²(8x² + 6x - 7) + 11x(8x² + 6x - 7) + 2(8x² + 6x - 7) [distribute the first polynomial]
= -72x⁴ - 54x³ + 63x² + 88x³ + 66x² - 77x + 16x² + 12x - 14 [multiply out each term]
= -72x⁴ + 34x³ + 95x² - 65x - 14 [combine like terms and simplify]
Therefore, (-9x² + 11x + 2) x (8x² + 6x - 7) = -72x⁴ + 34x³ + 95x² - 65x - 14
Can someone help please ?
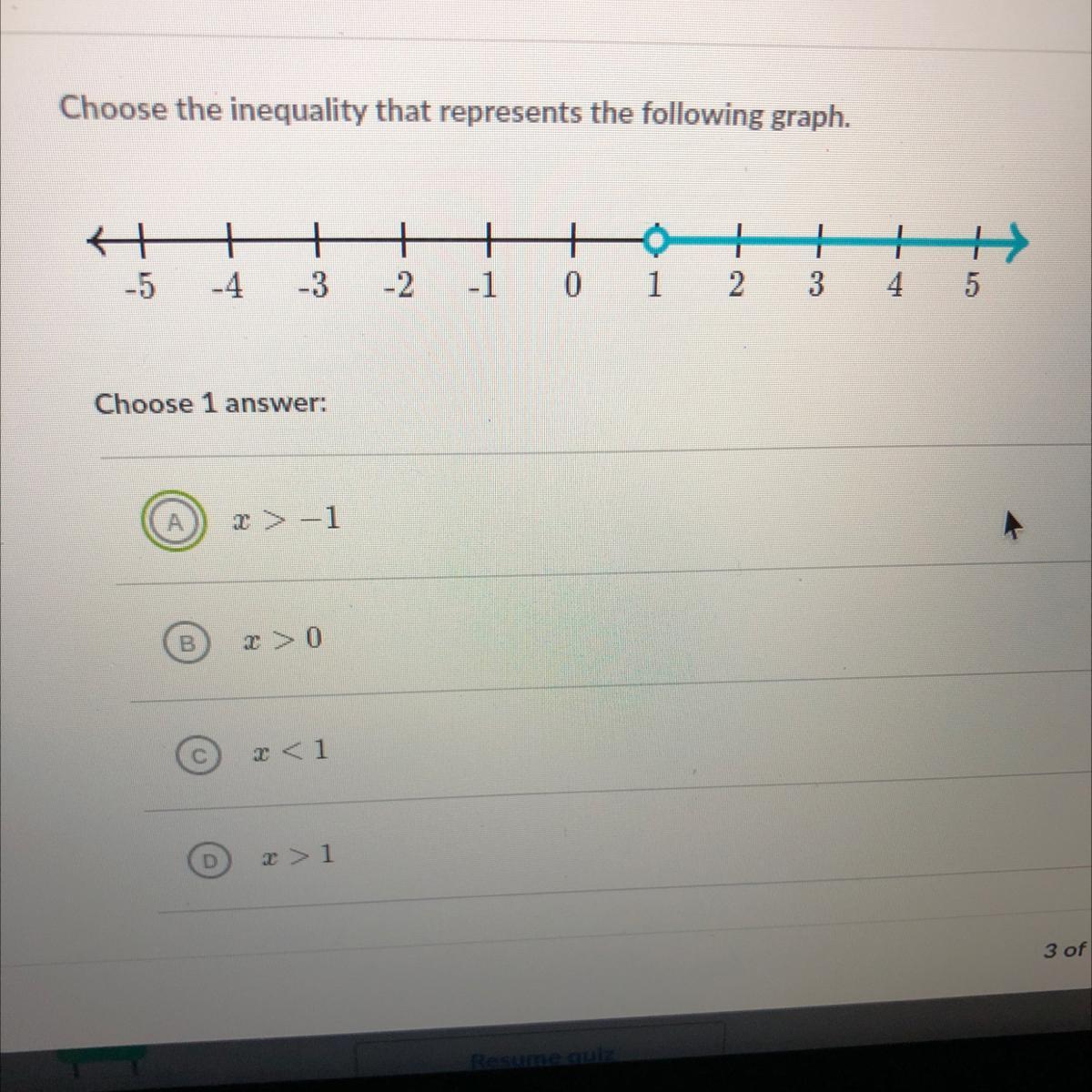
Answers
Answer:
The answer is D.
Answer:
i did this in Algebra 1
it's D.
Step-by-step explanation:
:)))
sketch the region enclosed by the given curves. y = cos(x), y = sin(2x), 0 ≤ x ≤ 2
Answers
To sketch the region enclosed by the curves y = cos(x) and y = sin(2x) for the interval 0 ≤ x ≤ 2, we can follow these steps:
1. Plot the graphs of the two functions separately on the given interval.
For y = cos(x):
- Start by marking key points on the graph: (0, 1), (π/2, 0), (π, -1), (3π/2, 0), (2π, 1).
- Connect the points smoothly to create a curve that oscillates between 1 and -1.
For y = sin(2x):
- Start by marking key points on the graph: (0, 0), (π/4, 1), (π/2, 0), (3π/4, -1), (π, 0), (5π/4, 1), (3π/2, 0), (7π/4, -1), (2π, 0).
- Connect the points smoothly to create a curve that oscillates between 1 and -1, but with twice the frequency of the cosine curve.
2. Identify the region enclosed by the curves.
- The region enclosed by the curves is the area between the two curves from x = 0 to x = 2.
3. Shade the region enclosed by the curves.
- Shade the area between the two curves on the interval 0 ≤ x ≤ 2.
To know more about curve region refer here:
https://brainly.com/question/14390012?#
#SPJ11
Find the area of an equilateral triangle with a perimeter of 45 inches.
Answers
The area of the equilateral triangle is approximately 58.78 square inches.
An equilateral triangle has all sides equal, so we can divide the perimeter by 3 :
45 inches ÷ 3 = 15 inches
Therefore, each side of the equilateral triangle measures 15 inches.
Area = (√3 / 4) x (side length)²
After putting the values,
Area = (√3 / 4) x 15 x 15 square inches
Area = (√3 / 4) x 225 square inches
Area = 58.78 square inches
Learn more about equilateral triangle
https://brainly.in/question/2036108
In testing a certain kind of truck tire over rugged terrain, it is found that 25% of the frucks fail to complete the test run without a blowout. Of the next 15 trucks tested, find the probability that (a) from 3 to 6 have blowouts; (b) fewer than 4 have blowouts: (c) more than 5 have blowouts.
Answers
Probability that from 3 to 6 have blowouts is 0.4477 Probability that fewer than 4 have blowouts is 0.3615Probability that more than 5 have blowouts is 0.3973.
Given: It is found that 25% of the trucks fail to complete the test run without a blowout.Probability is the ratio of the number of favorable outcomes to the total number of possible outcomes.In order to find the probability of the given events, we will use Binomial Distribution.
Let’s find the probability of given events one by one:a) From 3 to 6 trucks have blowouts Number of trials = 15 (n)Number of success = trucks with blowouts (x)Number of failures = trucks without blowouts = 15 - xProbability of a truck with blowout = p = 0.25Probability of a truck without blowout = q = 1 - 0.25 = 0.75We need to find
P(3 ≤ x ≤ 6) = P(x = 3) + P(x = 4) + P(x = 5) + P(x = 6)P(x = r) = nCr * pr * q(n-r)
where nCr = n! / r!(n-r)!P(x = 3)
= 15C3 * (0.25)3 * (0.75)12
= 0.1859P(x = 4) = 15C4 * (0.25)4 * (0.75)11
= 0.1670P(x = 5)
= 15C5 * (0.25)5 * (0.75)10 = 0.0742P(x = 6)
= 15C6 * (0.25)6 * (0.75)9 = 0.0206P(3 ≤ x ≤ 6)
= 0.1859 + 0.1670 + 0.0742 + 0.0206
= 0.4477
Therefore, the probability that from 3 to 6 trucks have blowouts is 0.4477.b) Fewer than 4 trucks have blowoutsNumber of trials = 15 (n)Number of success = trucks with blowouts (x)Number of failures = trucks without blowouts = 15 - xProbability of a truck with blowout = p = 0.25Probability of a truck without blowout = q = 1 - 0.25 = 0.75We need to find P(x < 4) = P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3)P(x = r) = nCr * pr * q(n-r)where nCr = n! / r!(n-r)!P(x = 0) = 15C0 * (0.25)0 * (0.75)15 = 0.0059P(x = 1) = 15C1 * (0.25)1 * (0.75)14 = 0.0407P(x = 2) = 15C2 * (0.25)2 * (0.75)13 = 0.1290P(x = 3) = 15C3 * (0.25)3 * (0.75)12 = 0.1859P(x < 4) = 0.0059 + 0.0407 + 0.1290 + 0.1859= 0.3615Therefore, the probability that fewer than 4 trucks have blowouts is 0.3615.c) More than 5 trucks have blowoutsNumber of trials = 15 (n)Number of success = trucks with blowouts (x)Number of failures = trucks without blowouts = 15 - xProbability of a truck with blowout = p = 0.25Probability of a truck without blowout = q = 1 - 0.25 = 0.75
We need to find P(x > 5)P(x > 5) = P(x = 6) + P(x = 7) + ... + P(x = 15)P(x = r) = nCr * pr * q(n-r)
where nCr = n! / r!(n-r)!
P(x > 5) = 1 - [P(x ≤ 5)]P(x ≤ 5) = P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) + P(x = 4) + P(x = 5)P(x = 0) = 15C0 * (0.25)0 * (0.75)15
= 0.0059P(x = 1) = 15C1 * (0.25)1 * (0.75)14 = 0.0407P(x = 2)
= 15C2 * (0.25)2 * (0.75)13 = 0.1290P(x = 3)
= 15C3 * (0.25)3 * (0.75)12 = 0.1859P(x = 4)
= 15C4 * (0.25)4 * (0.75)11 = 0.1670P(x = 5)
= 15C5 * (0.25)5 * (0.75)10
= 0.0742P(x ≤ 5)
= 0.0059 + 0.0407 + 0.1290 + 0.1859 + 0.1670 + 0.0742
= 0.6027P(x > 5) = 1 - 0.6027= 0.3973
Therefore, the probability that more than 5 trucks have blowouts is 0.3973.Answer:Probability that from 3 to 6 have blowouts is 0.4477Probability that fewer than 4 have blowouts is 0.3615Probability that more than 5 have blowouts is 0.3973.
To know more about Probability Visit:
https://brainly.com/question/31828911
#SPJ11
I WILL GIVE BRAINLIEST THIS IS EASY PLS HELP ASAP
Match each term with its definition.
Perpendicular lines?
Angle?
Line segment?
Parallel lines?
Circles?

Answers
Ah bg de cf
Step-by-step explanation:
i think thats how you do it becuse i did that
For B the answer is 3
For C the answer is 5
For D the answer is 1
For E the answer is 2
Simplify the expression. Assume that x is nonzero. Your answer should have only positive exponents.
Equation:
x^-10 · x^6
Please help me out.
Answers
Answer: x^-4
Step-by-step explanation:
x^-10 · x^6
When you're multiplying exponents, use the first rule: add powers together when multiplying like bases.
-10 + 6 = -4
x^-4
the sum of three nonnegative numbers is 36, and one of the numbers is twice one of the other numbers. what is the maximum value of the product of these three num- bers?
Answers
324 is the maximum value of the product of these three numbers
What is maxima and minima?
The curve of a function has peaks and troughs called maxima and minima. A function may have any number of maxima and minima. Calculus allows us to determine any function's maximum and lowest values without ever consulting the function's graph. Maxima will be the curve's highest point within the specified range, and minima will be its lowest.
The extrema of a function are the maxima and minima. The maximum and minimum values of a function inside the specified ranges are known as maxima and minima, respectively. Absolute maxima and absolute minima are terms used to describe the function's maximum and minimum values, respectively, over its full range.
Let the three nonnegative numbers are x,y,z
According to the question
x+y+z=36
and y=2x
therefore, 3x+z=36--------------------------------------------------(1)
z=36-3x
Let 3xz= u--------------------------------------------------------------(2)
differentiating equation 2
du/dx=3z + 3xdz/dx
or
du/dx= z + xdz/dx
differentiating equation 1
3 + dz/dx = 0
dz/dx = -3
du/dz = 36-3x + x(-3)
du/dx = 12 - 2x--------------------------------------------------------------(3)
for maxima put du/dx = 0
x=6-------------------------------------------------------------------------------(4)
again differentiating du/dx = 12 - 2x
d2u/dx2=-2
which means 3xz= u is maximum at x=6
from equation 1 and 4
we get 18+z=36
z=18
Therefore 3xz= 3(6)(18)=324
Learn more about Maxima and Minima from the link below
https://brainly.com/question/12870695
#SPJ4
A grocer mixed together some cashews costing $8 per kilogram
Answers
9 kilograms of cashews were mixed with 3 kilograms of nuts to make 12 kg of the mixture.
What are the arithmetic operations?
The four basic mathematical operations are Addition, subtraction, multiplication, and division.
Let's assume that x kilograms of cashews were mixed with (12 - x) kilograms of nuts costing $10 per kilogram to make 12 kg of the mixture.
The total cost of the cashews used in the mixture is 8x dollars, and the total cost of the nuts used is 10(12 - x) dollars. The total cost of the mixture is (12)(8.50) = 102 dollars.
Since the mixture contains 12 kg of nuts and cashews, we can set up the following equation to solve for x:
8x + 10(12 - x) = 102
Expanding the equation gives:
8x + 120 - 10x = 102
Simplifying and solving for x gives:
-2x + 120 = 102
-2x = -18
x = 9
Hence, 9 kilograms of cashews were mixed with 3 kilograms of nuts to make 12 kg of the mixture.
To learn more about arithmetic operations, Visit
https://brainly.com/question/20628271
#SPJ1
hello cn someone help please

Answers
The size of angle x is 54 degrees.
Let O be the complete angle,
<O = 360
Angle between diagonals = 360/5 = 72 degrees.
All diagonals of regular pentagon are equal and their opposite angles are equal .
With angle center O it forms a triangle:
sum of angles = 180
x + x + 72 = 180
2x + 72 = 180
2x = 180 - 72
2x = 108
divide by 2 on both sides
2x/2 = 108/2
x = 108/2
x = 54 degrees.
Therefore the size of angle x is 54 degrees.
Learn more about the regular pentagon and angle here:
https://brainly.com/question/26522820
#SPJ1
