14) Out of the following options, pick the one that
can be expressed as a rational number.
a) 1.16321632...
b) 0.00120345...
c) 5.672101234 ...
d) 2.75757575...
i have no idea what this means
Answers
Related Questions
Harriet and Maya share £300 in the ratio of 7:5. Wirk out how much money harriet gets
Answers
Answer:
$175
Step-by-step explanation:
you need to specify if harriet got the 7 portion or the 5 portion. I'll answer as if she got the 7 portion.
They split it into 12 portions because the ratio is 7:5 and 7+5=12. So do $300/12=25
Assuming Maya got the 5 portion, do $25 x 5 = $125, so Maya got $125.
Assuming Harriet got the 7 portion, do $25 x 7 = $175, so Harriet got $175.
Solve the linear system of equations
3x+2y=7
-3x+4y=5
X=
Y=
Answers
X= 1 , Y = 2
Step-by-step explanation :

Help ASAP DUE IN 15 MINUTES!!



Answers
Answer:
b and c
Step-by-step explanation:
i just know
Original price: ?
Percent of discount: 25%
Sale price: $45
Answers
Answer:
Original price is 11.25
Step-by-step explanation:
Answer: 60
The percent of sale price is 100% - 25% = 75%
the original price is (45/75).100 = 60$
Step-by-step explanation:
a dice is rolled 60 times, what is the probability of it landing on 4
Answers
Find the normal approximation to the chance that the face with six spots appears between 9, 10, or 11 times.
The exact chance that the face with six spots appears 9, 10, or 11 times?
my solution; in one roll of the die P(6 spots)=16 In 60 rolls of the die the expected number of times the face with 6 spots appears is given by E(X)=Mean=606=10 times.
SE(6spots)=SD=SQR(606⋅56)=2.8868
Applying the normal approximation to the chance that the face with six spots appears 10 times, I obtain the following: mean = 10
Standard deviation=2.8868
Using the continuity correction of 0.5 the following z-scores are found: z1=(9.5−10)/2.8868=−0.1732 and z2=(10.5−10)/2.8868=0.1732 Subtracting the cumulative probabilities for the two z-scores gives 0.5688−0.4312=0.1376 which is the approximate chance that the face with six spots appears 10 times. find the six spots appears between 9,10, or 11?
The exact chance that the face with six spots appears 10 times is found from
60C10(16)10×(56)50=0.137 find six spots appears 9, 10 or 11 times
Michelle fills up her tank at the gas station. She puts 13.5 gallons of gas in her car, and it cost $34.60. What is the unit rate she paid for gas, in dollars per gallon?
Answers
9514 1404 393
Answer:
$2.563
Step-by-step explanation:
To find dollars per gallon, divide dollars by gallons.
$34.60/(13.5 gal) ≈ $2.563 /gal
Michelle paid about $2.563 per gallon.
__
Additional comment
We have reported the price to the nearest 1/10th cent, as that is the way gas prices are usually posted.
Unit Test
Active
1
2
What is the value of S4 for
58
O 375
5
O 36
208
O 375
104
125
n-1
23(3),
?
n=1
Answers
The sum of five terms is 208/375 or the value of S(4) is 208/375 option third is correct.
What is a sequence?It is defined as the systematic way of representing the data that follows a certain rule of arithmetic.
The question is incomplete.
The complete question is in the picture, please refer to the attached picture.
We have:
\(\rm \sum_{n=1}^\infty\dfrac{2}{3}(\dfrac{-1}{5})^{n-1}\)
Plug n = 1
We will get the first term:
a = 2/3
The sum of the terms of a geometric sequence is given by the formula:
\(\rm S_n = \dfrac{a(1-r^n)}{1-r}\)
r = -1/5
\(\rm S_4 = \dfrac{a(1-(-1/5)^4)}{1-(-1/5)}\)
After solving:
S(4) = 208/375
Thus, the sum of five terms is 208/375 or the value of S(4) is 208/375 option third is correct.
Learn more about the sequence here:
brainly.com/question/21961097
#SPJ1

4. Write the following quadratics as products of two binomials. f(x) = 6x2 + 66x + 60
Answers
Answer:
f(x)=(6x+6)(x+10)
Explanation:
Given the quadratic expression:
\(f\mleft(x\mright)=6x^2+66x+60\)First, we can rewrite it in the form below:
\(f\mleft(x\mright)=6x^2+60x+6x+60\)Next, factor the terms:
\(\begin{gathered} f(x)=6x(x+10)+6(x+10) \\ \implies f(x)=(6x+6)(x+10) \end{gathered}\)Thus, the quadratics as a product of two binomials is:
\(f(x)=(6x+6)(x+10)\)A local pizza shop has a membership program for frequent buyers. The membership costs $5 per month and members get a discounted price of $1.75 per slice of pizza. Lamonte purchased a membership to this pizza shop. How much would Lamonte have to pay the pizza shop if he bought 20 slices of pizza this month? What would be the monthly cost for x slices of pizza?
monthly cost with 20 slices:
monthly cost with x slices
Answers
Answer:
monthly cost with 20 slices:
5 + (1.75 x 20)
5+35
40
monthly cost with x slices:
1.75x + 5
Hope this helps!
please help it will be helpful
Equivalent Ratio
9:36=
21:27=
48:72=
60:45=
10:70=
Answers
7:9
5:9
4:3
1:7
Hope this helps :)
use the following to answer the next 2 questions. solar-heat installations successfully reduce the utility bill 60% of the time. suppose 10 houses with solar-heat installations are selected at random and the outcome between houses is independent. suppose x is the number of houses that successfully reduced the utility bill out of the 10. 14. which discrete distribution will appropriately model x? explain. binomial 15. what is the probability that at least 9 out of 10 solar-heat installations are successful and will reduce the utility bill? a. 0.0464 b. 0.9432 c. 0.0403 d. 0.8429
Answers
The probability that at least 9 out of 10 solar-heat installations will succeed and reduce the utility bill is 0.0464.
What is a binomial distribution?
The probability distribution known as the binomial distribution, which is used in statistics, quantifies the chances that a value will take one of two independent values given a particular set of conditions or hypotheses.
Formula to calculate the binomial distribution
P(X = x) =ⁿCₓ× pˣ×(1-p)ⁿ⁻ˣ
Here, we know that
Solar-heat installations successfully reduce the utility bill 60% of the time.
We have to calculate the probability that at least 9 out of 10 solar-heat installations will succeed and reduce the utility bill.
We have 60% = 0.6 = p and n = 10.
We have a binomial distribution: X : (10, 0.6).
We use the binomial distribution formula to calculate the probability
P(X = x) =ⁿCₓ× pˣ×(1-p)ⁿ⁻ˣ, we get
P(x ≥ 9) = 1 - P(x < 9)
P(x ≥ 9) = 1 - P(x ≤ 8)
P(x ≥ 9) = 1 - ∑⁸₀ P(x = x)
P(X ≥ 9) = 1 - ∑⁸₀¹⁰Cₓ × (0.6)ˣ × (1-0.6)¹⁰⁻ˣ
P(X ≥ 9) = 1 -( 0.00011 + 0.00157 + 0.01062 + 0.04247 + 0.11148 + 0.20066 + 0.25082 + 0.21499 + 0.12093)
P(X ≥ 9) = 1 -0.95365
P(X ≥ 9) = 0.04635
Hence, the probability that at least 9 out of 10 solar-heat installations will succeed and reduce the utility bill is 0.0464.
To learn more about the binomial distribution from the given link
https://brainly.com/question/15223696
#SPJ4
Please explain...
y=3x^2-5x+1 solve by completing the square
Answers
Answer:
x=5+√136or x=5−√136
Step-by-step explanation:
To solve this equation we have to factorize 3x2−5x+1. Since we can not use any
Suppose that Y 1
,…,Y n
are i.i.d. N(μ,σ 2
), where μ is known. Show that the MLE of σ 2
is n −1
∑ i=1
n
(Y i
−μ) 2
Answers
The correct value of the MLE of \(\hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^{n}(Y_i - \mu)^2\)
To find the maximum likelihood estimator (MLE) of σ^2 given the i.i.d. normal random variables Y1, ..., Yn with known mean μ, we need to maximize the likelihood function.The likelihood function for a normal distribution is given by:
\(L(\sigma^2) = \left(\frac{1}{\sqrt{2\pi\sigma^2}}\right)^n \cdot \exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(Y_i - \mu)^2\right)\)
To find the MLE of σ^2, we maximize the log-likelihood function (logarithm simplifies calculations):
\(\log(L(\sigma^2)) = -\frac{n}{2}\log(2\pi) - \frac{n}{2}\log(\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^{n}(Y_i - \mu)^2\)
To maximize the log-likelihood, we differentiate it with respect to σ^2 and set the derivative to zero:
\(\frac{d}{d(\sigma^2)} \log(L(\sigma^2)) = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_{i=1}^{n}(Y_i - \mu)^2 = 0\)
Simplifying, we get:
nσ^2 + ∑(Yi - μ)^2 = 0
Rearranging the equation, we have:
σ^2 = (1/n)∑(Yi - μ)^2
This expression is the MLE of σ^2, which is the sample variance of the differences between each observation Yi and the known mean μ, divided by n.Therefore, the MLE of σ^2 is (1/n)∑(Yi - μ)^2.
Learn more about statistics here:
https://brainly.com/question/30915447
#SPJ11
I'm genuinely confused

Answers
Answer:
Basically what you wanna do is find all points on the x axis since it is at 0 y
So the answer is -2 1 or 3 only
Construct a counterexample by model for the following invalid argument, and then explain exactly how your counterexample proves that the argument is invalid.
¼ of the hairs in Plato’s beard are gray. ¾ of the hairs in Aristotle’s beard are gray. So, Aristotle has a greater number of gray hairs in his beard than Plato does.
Answers
The given argument is invalid. It says that if one person has more gray hair in their beard than another person, then they have a higher percentage of gray hair in their beard.
The argument is invalid because it is possible for one person to have a higher percentage of gray hair in their beard but a lower number of gray hairs in total.One possible counterexample by model is:Suppose Plato has 200 hairs in his beard and 50 of them are gray. So, 1/4 of his hairs are gray. Now, let's suppose Aristotle has 400 hairs in his beard, and 300 of them are gray. So, 3/4 of his hairs are gray. Even though Plato has fewer gray hairs than Aristotle, his percentage of gray hairs is more significant (1/4) than Aristotle's (3/4).
Therefore, the given argument is invalid since Aristotle's beard contains more gray hairs in quantity, but Plato has a higher percentage of gray hair in his beard.
Learn more about argument here:
brainly.com/question/2645376
#SPJ11
The school cafeteria serves cheese and pepperoni pizza. A random survey was given to 175 students to find out which kind of pizza students prefer. Of the students surveyed, 80 students preferred pepperoni pizza. If the school has a population of 400 students, how many students would be expected to choose cheese pizza?
Answers
Answer: 145
Step-by-step explanation:
I hope the answer is correct
I am not so sure of it though
The number of students that would be expected to choose cheese pizza is 217.
What is the ratio?The ratio is a numerical relationship between two values that demonstrates how frequently one value contains or is contained within another.
Given:
Cheese and pepperoni pizzas are served by the school cafeteria.
To find the preference for pizzas:
A random survey was given to 175 students.
The pepperoni pizza was preferred by 80 students.
That means the ratio of preference for cheese pizza = (175 - 80)/175
= 0.54
The population of the school is 400 students.
The number of students that would be expected to choose cheese pizza is,
= 400 x 0.54
= 217.1
≈ 217 students.
Therefore, the required number of students is 217 students.
To learn more about the ratio;
https://brainly.com/question/13419413
#SPJ6
Are the expressions -0.5(3x + 5) and
-1.5x + 2.5 equivalent? Explain why or why not.

Answers
Answer:
No, because the first equation equals -1.5x + 2.5 when simplified, but when the second equation is simplified it equals 1
Find the slope of the line through each pair of points.
(-18, 7), (-10, -15)
Answers
The entered points belong to a decreasing, linear function.
Equation: y = -2.75x - 42.5.

Answer:
slope = - \(\frac{11}{4}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 18, 7 ) and (x₂, y₂ ) = (- 10, - 15 )
m = \(\frac{-15-7}{-10-(-18)}\) = \(\frac{-22}{-10+18}\) = \(\frac{-22}{8}\) = - \(\frac{11}{4}\)
Help please this is due today!!!
please provide a small explanation!!

Answers
Answer:
200 sq cm
Step-by-step explanation:
Lateral surface area is the surface area without the bases, or without the top and bottom. So, you just add up the area of the 4 sides.
The front and back are both 10 x 20, so 200 each = 400
The left and right are 5 x 20, so 100 each = 200
The lateral surface area is 200 sq. cm.
the sum of three numbers $x$ ,$y$, $z$ is $165$. when the smallest number $x$ is multiplied by $7$, the result is $n$. the value $n$ is obtained by subtracting $9$ from the largest number $y$. this number $n$ also results by adding $9$ to the third number $z$. what is the product of the three numbers?
Answers
The product of three numbers is 12,295.
We are given that the sum of three numbers x, y, and z is 165, so we can write:
x + y + z = 165
We are also told that when the smallest number x is multiplied by 7, the result is n. So we can write:
x * 7 = n
It is also given that the value n is obtained by subtracting 9 from the largest number y, so we can write:
y - 9 = n
And that this number n also results by adding 9 to the third number z, so we can write:
z + 9 = n
We have 3 equations with 3 unknowns, we can use these equations to solve the problem.
From the equation x * 7 = n, we can substitute n = y-9, and we get:
x * 7 = y - 9
From the equation z + 9 = n, we can substitute n = y-9, and we get:
z + 9 = y - 9
Now we have 2 equations with 3 unknowns x,y,z.
To solve for the third unknown, we can use the equation x + y + z = 165 and substitute the values that we know from the previous equations:
x + (y - 9) + (z + 9) = 165
Solving for x we get:
x = (165 - (y-9) - (z+9)) = (165 - y + 9 - z - 9) = (165 - y - z + 18) = (183 - (y+z))
Now we can substitute this value into one of the previous equations:
(183 - (y+z)) * 7 = y - 9
Solving for y and z we get:
y = 95 and z = 71
And the product of the three numbers is:
x * y * z = (183 - (y+z)) * y * z = (183 - (95 +71)) * 95 * 71 = (183 - 166) * 95 * 71 = 17 * 95 * 71 = 12,295
So the product of three numbers is 12,295.
To learn more about the product, visit:
brainly.com/question/3211849
#SPJ4
5.6 divided by -36 (please show the work)
Answers
Answer:
-11.2
Step-by-step explanation:
2(3m+6n) + 3(5m-2n)+ 5(-6m+n)
Answers
Answer:
\(2(3m + 6n) + 3(5m - 2n) + 5( - 6m + n) \\ \)
open the brackets:
\( = (6m + 12n) + (15m - 6n) + ( - 30m + 5n) \\ \)
group the coefficients of m and n in their brackets:
\( = (6 + 15 - 30)m + (12 - 6 + 5)n \\ \)
then operate the brackets:
\( = - 9m + 11n\)
Assume that in a given year the mean mathematics sat score was 572, and the standard deviation was 127. a sample of 72 scores is chosen. What is the probability that the sample mean score is less than 567?
Answers
According to the Central Limit Theorem, for a sufficiently large sample size, the distribution of sample means will be approximately normal, regardless of the shape of the population distribution.
To calculate the probability, we need to convert the sample mean score to a z-score and then find the corresponding area under the standard normal distribution curve.
Calculate the standard error of the mean (SE):
SE = σ / sqrt(n)
SE = 127 / sqrt(72)
SE ≈ 14.96
Calculate the z-score:
z = (X - μ) / SE
z = (567 - 572) / 14.96
z ≈ -0.334
Find the probability corresponding to the z-score:
We can find the area to the left of the z-score -0.334. Let's denote this probability as P(z < -0.334).
The probability that the sample mean score is less than 567 is approximately equal to P(z < -0.334).
Learn more about Central Limit Theorem here : brainly.com/question/898534
#SPJ11
Caculate the unit rate. A ball drops 160 feet in 4
seconds. How many feet dropped per second?
Answers
Answer:40ft/second
Step-by-step explanation:
Divide 160ft by 4sec to find the unit rate.
Answer:
40
Step-by-step explanation:
You would divide 160 by 4 to get the number of feet dropped in one second. 160 divided by 4 is 40
Hope this helps! Good luck :)
Solve the following: five and one tenth − two and eight tenths
Answers
Answer:
Step-by-step explanation:
The first thing we need to do is set up the problem.
5\(\frac{1}{10}\) - 2\(\frac{8}{10}\)
After we do this, we have to combine the whole numbers into the fraction to make an improper fraction.
5\(\frac{1}{10}\) becomes \(\frac{51}{10}\) because we get 5 times 10 + 1.
2\(\frac{8}{10}\) becomes\(\frac{28}{10}\) because we get 2 times 10 + 8.
After doing this we can subtract and get the answer.
51 - 28 = 23
So the answer is \(\frac{23}{10}\).
Please help asap it's pretty easy!!! Explain I will give brainliest if right!

Answers
Answer:
ABC
Step-by-step explanation:
Use the law of sines to find the length of side c

Answers
Answer:
B. 44.93
Step-by-step explanation:
The law of sines states
\(\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}\)
where a, b and c are the 3 sides of the triangle and A is the angle opposite side a, B the angle opposite side b and C the angle opposite side c
In this particular problem we have
side a = 44, angle A = 46.7
side c = ? , angle C = 48
So 44/sin(46.7) = c/sin(48) or by multiplying both sides by sin(48)
c = sin(48) * 44/sin(46.7) = 44.92937 which is 44.93 rounded to 2 decimal places
You have $100 in your bank account. If it doubles every month and you started back in Jarwary.
how much money will you have by May?
Answers
Answer:
I think 1,600
Step-by-step explanation:
solve this problem pls
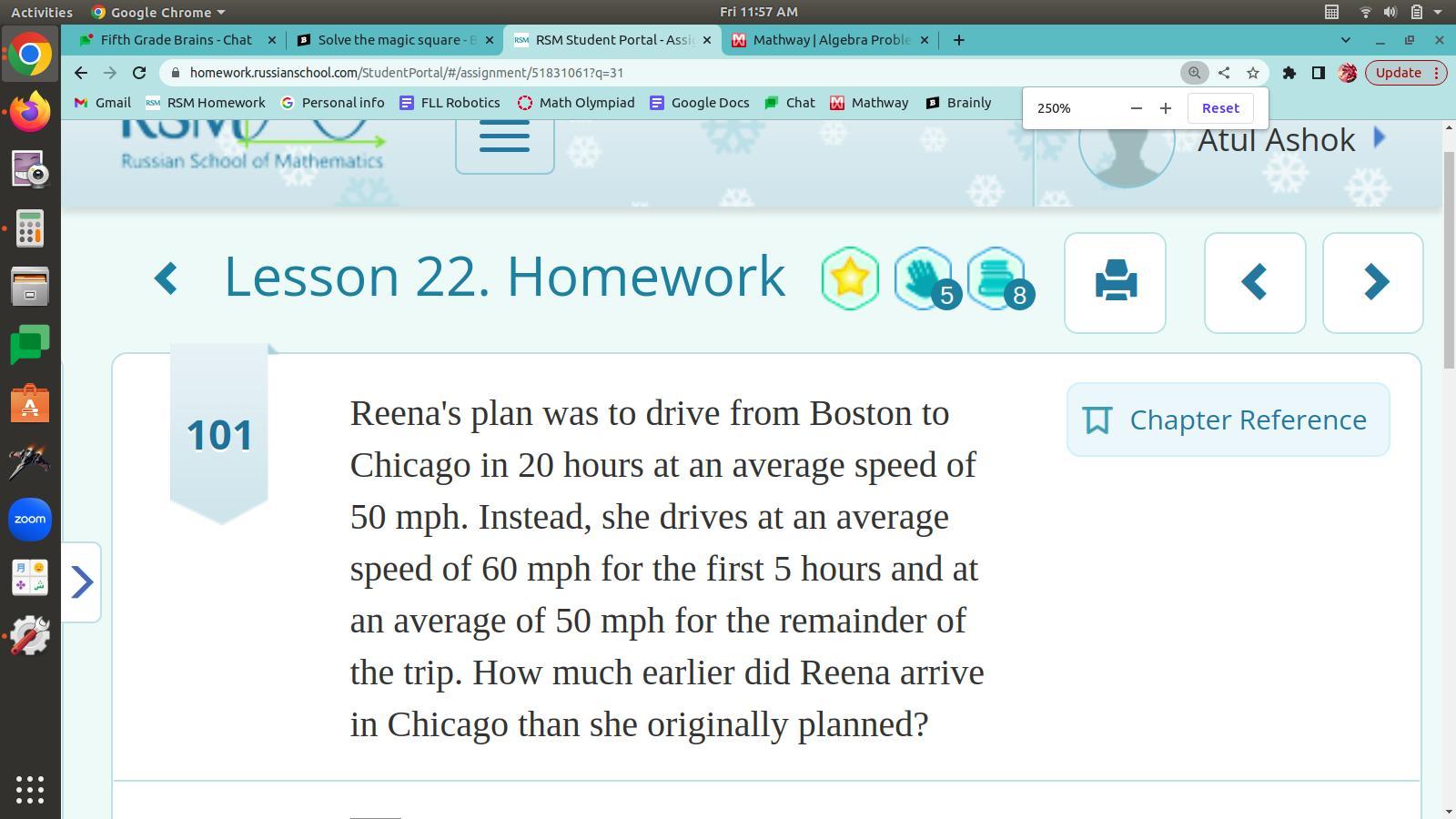
Answers
Reena's original speed as compared to her new speed concludes that Reena arrived at her destination in her planned amount of time which is 20 hours.
What is speed?
The distance travelled in relation to the time it took to travel that distance is how speed is defined. Since speed simply has a direction and no magnitude, it is a scalar quantity.
Reena's original plan was to drive for 20 hours at an average speed of 50 mph, which means that she would have covered a distance of -
Distance = Speed x Time
Distance = 50 mph x 20 hours
Distance = 1000 miles
Now calculate the distance that Reena actually traveled.
She drove at an average speed of 60 mph for the first 5 hours, covering a distance of -
Distance1 = Speed1 x Time1
Distance1 = 60 mph x 5 hours
Distance1 = 300 miles
For the remaining 15 hours of the journey, she drove at an average speed of 50 mph, covering a distance of -
Distance2 = Speed2 x Time2
Distance2 = 50 mph x 15 hours
Distance2 = 750 miles
The total distance that Reena traveled is the sum of the two distances -
Total Distance = Distance1 + Distance2
Total Distance = 300 miles + 750 miles
Total Distance = 1050 miles
Reena actually traveled 1050 miles to reach Chicago, which is 50 miles more than her planned distance of 1000 miles.
To calculate how much earlier Reena arrived in Chicago than she originally planned, we need to compare the time it took her to travel the two distances -
Time1 = Distance1 / Speed1
Time1 = 300 miles / 60 mph
Time1 = 5 hours
Time2 = Distance2 / Speed2
Time2 = 750 miles / 50 mph
Time2 = 15 hours
Total Time = Time1 + Time2
Total Time = 5 hours + 15 hours
Total Time = 20 hours
Reena arrived in Chicago in 20 hours, which was exactly the same as her original plan.
Therefore, she did not arrive earlier than planned.
To learn more about speed from the given link
https://brainly.com/question/6504879
#SPJ1
If (4x + 1) is one of the factors of p(x) = 4x³ + 5x² - 23x - 6, then p(x) = 0 when x =
Options :
A. 1/4
B. 1/2
C. -1/2
D. -1/4
no spam and kindly explain your answer!
Answers
Answer:
THE CORRECT OPTION IS DGiven
4x+1 is a factor of p(x) = 4x³ + 5x² - 23x - 6,
so
4x+1 =0
4x = -1
x = -1/4
Answer -p(x) = 0 when x = -1/4