-14x + 18 - 11 -2x + 3
Answers
Answer:
-2(8x-5)
Step-by-step explanation:
Answer:
I think you meant -14x+18-11-2x+3=0
If that's the case then x= 5/8
Step-by-step explanation:
-16x+10=0
-16x= -10
x= -10/-16 = 5/8
In decimal form it is 0.625
Related Questions
consider two nonnegative numbers p and q such that p+q=6. what is the difference between the maximum and minimum of the quantity (p^2q^2)/2?
Answers
When considering two nonnegative numbers p and q such that p+q=6, the difference between the maximum and minimum of the quantity (p^2q^2)/2 is 81 - 0 = 81.
To find the maximum and minimum of the quantity (p^2q^2)/2, we can use the AM-GM inequality.
AM-GM inequality states that for any nonnegative numbers a and b, (a+b)/2 ≥ √(ab).
So, in our case, we can write:
(p^2q^2)/2 = (p*q)^2/2
Let x = p*q, then we have:
(p^2q^2)/2 = x^2/2
Since p and q are nonnegative, we have x = p*q ≥ 0.
Using the AM-GM inequality, we have:
(x + x)/2 ≥ √(x*x)
2x/2 ≥ x
x ≥ 0
So, the minimum value of (p^2q^2)/2 is 0.
To find the maximum value, we need to use the fact that p+q=6.
We can rewrite p+q as:
(p+q)^2 = p^2 + 2pq + q^2
36 = p^2 + 2pq + q^2
p^2q^2 = (36 - p^2 - q^2)^2
Substituting this into the expression for (p^2q^2)/2, we get:
(p^2q^2)/2 = (36 - p^2 - q^2)^2/2
To find the maximum value of this expression, we need to maximize (36 - p^2 - q^2)^2.
Since p and q are nonnegative and p+q=6, we have:
0 ≤ p, q ≤ 6
So, the maximum value of (36 - p^2 - q^2) occurs when p=q=3.
Thus, the maximum value of (p^2q^2)/2 is:
(36 - 3^2 - 3^2)^2/2 = 81
Therefore, the difference between the maximum and minimum of (p^2q^2)/2 is:
81 - 0 = 81.
Learn more about maximum and minimum of the quantity:
https://brainly.com/question/29671614
#SPJ11
The union of two sets is a set that contains only the elements that appear in both sets
a. True
b. False
Answers
The union of two sets is to avoid counting the same elements twice.
What is set?
The mathematical logic subfield of set theory investigates sets, which can be loosely defined as collections of objects. Although any object can be combined into a set, set theory, as a mathematical discipline, focuses primarily on those that are relevant to mathematics as a whole.
Given union of set
(A ∪ B),
The set of all objects that are members of either A or B, or both, is the union of the sets A ∪ B.
let us take example,
A = { 1, 2, 3, 4}
B = {3, 4, 5, 6, 7}
(A ∪ B) = { 1, 2, 3, 4} ∪ {3, 4, 5, 6, 7}
we can simply write all of A and B's elements in a single set to avoid duplicates to find A U B.
(A ∪ B) = {1, 2, 3, 4, 5, 6, 7}
Hence the union of two sets is a set that contains all the elements of both set and avoid duplicates.
Learn more about set;
https://brainly.com/question/28492445
#SPJ12
You have 6 different colored balloons. In how many distinct ways can the balloons be ordered?
Select one:
a.
720
b.
365
c.
5040
d.
120
Answers
Answer: a. 720
Step-by-step explanation:
You have 6 different sticks to choose from for the first stick. Then there are 5 for the second (6 - 1 = 5), then 4 for the third (5 - 1 = 4), etc all the way to the last stick.
Mathematically, this can be shown with 6!. In other words, 6 factorial.
6 * 5 * 4 * 3 * 2 * 1 = 720
The answer to our question is:
a. 720
Please help me long division step by step !!!

Answers
Answer:
0.850
Step-by-step explanation:
The first step is to write the number in standard form. Then, you place the decimal point in the quotient above the decimal point of the dividend. Then, divide and bring down the other digits such as hundredths, thousandth, and ect.

whats 2÷1 to the 2nd power
Answers
Answer: its going to be 2
Step-by-step explanation: simplify 1 to the second power would be 1*1 and 2 divide by 1 is 2 hope this helps :D
Answer:
4
Step-by-step explanation:
Write the equation of the line that passes through the points (2,5) and (-7,-2)
Answers
Answer:
y=7/9x+31/9
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(-2-5)/(-7-2)
m=-7/-9
m=7/9
y-y1=m(x-x1)
y-5=7/9(x-2)
y=7/9x-14/9+5
y=7/9x-14/9+45/9
y=7/9x+31/9
Shaan walks 2.5 meters per second. His brother Dhvan walks 1 meter
per second. Dhvan wants to have a race. Shaan knows that he walks faster,
but he wants to give his brother a head start of 45 meters, so it doesn't
seem that he is allowing him to win. How many meters long should the
race be in order for Dhvan to win?
Answers
Answer:
The race must be up to 29 meters for Dhvan to win.
Step-by-step explanation:
Since Shaan walks 2.5 meters per second, while his brother Dhvan walks 1 meter per second, and Dhvan wants to have a race, and Shaan knows that he walks faster, but he wants to give his brother a head start of 45 meters, so it doesn't seem that he is allowing him to win, to determine how many meters long should the race be in order for Dhvan to win the following calculation must be performed:
45 / (2.5 - 1) = X
45 / 1.5 = X
30 = X
Therefore, the race must be up to 29 meters for Dhvan to win.
Describe four common ways in which individuals respond to perceived inequity. provide an example of each.
Answers
Describe four common ways in which individuals respond to perceived inequity are -
People work hard to achieve and maintain equity.If perceive inequity, it causes conflict, which motivates them to reduce or eliminate it.The more severe the degree of inequity, the more motivated people are to decrease or eliminate a certain tension.Unfavorable inequity is more easily perceived than favorable inequity.What is equity?Equity, also known as shareholders' equity (or shareholders' equity for private companies), is the sum of money which would be handed back to a company ’s creditors if each of its assets have been liquidated and all of its debt was paid off in the event of liquidation.
Some key features regarding the equity are-
Equity is the value which would be returned to a company's shareholders if all assets have been liquidated and all debts were paid off.Equity can also be defined as the amount of leftover ownership in an organization or asset remaining after deducting all debts affiliated with that asset.On a company's balance sheet, equity represents the shareholders' stake in the company.Equity is calculated as a firm's revenue assets less total liabilities, and it is included in several important financial ratios like ROE.Home equity is another way to define equity. It is the value of an owner's estate (net of debt).To know more about the equity, here
https://brainly.com/question/12781629
#SPJ4
Eric's Ford Mustang and Susan's Toyota Prius are insured with the same insurance agent. They have 100/300/50 vehicle insurance coverage. The very week of the windstorm, Susan had an accident. She lost control of her car, hit a parked car, and damaged a storefront. The damage to the parked car was $4,300 and the damage to the store was $50,400. What amount will the insurance company pay for Susan's car accident?
Answers
Step-by-step explanation:
Given:
The damage to the parked car was
$4,300and the damage to the store
was
$50,400.
Objective:
The objective is to determine the
amount will the insurance company pay
for Susan's car accident.
Explanation:
Having a 100/300/50 insurance policy
means you have $100,000 in coverage
for bodily injury liability per person,
$300,000 for bodily injury liability per
accident, and $50,000 for property
damage liability.
The anmount insurance company
will pay $4,300 for car damage and
$50,000 for property damage.
So total amount that must be paid is
$50000+$4300=$54300
mark brainly

Which of the following is equivalent to the quotient below?
√135/√3
A. 5√3
B. √45/3
C. 3√5
D. 3√15
Answers
The answer is C. 3√5.
√135/√3√45√3² × 53√5What geometric shapes are in the fools puzzle quilt
Answers
The quilt consist of the following geometric shapes, which are the areas
bounded by lines, including;
An octagonA pentagonA right isosceles triangleAn equilateral triangleHow can the geometric shapes in the quilt be found?
Geometric shapes are shapes with boundary lines, interior angles and
surfaces.
The possible given quilt is attached;
From the given quilt, we have;
An octagon
A pentagon
A right isosceles triangle
An equilateral triangle
Learn more about types of geometric shapes here:
https://brainly.com/question/1259159

How many runners finished the race in under 13 minutes.
It's a 1.5 race.

Answers
Answer:
16 runners
Step-by-step explanation:
you have to add up all the runners that are under 13 minutes. Which is, 8+6+2 = 19 runners
Identify the correct test statistic for their significance test.

Answers
This is the alternative hypothesis. It is expressed as
H0 : μ < 250
How to solveA restaurant advertises that its burritos weigh 250 g. A consumer advocacy group doubts this claim, and they obtain a random sample of these burritos to test if the mean weight is significantly lower than 250 g. Let u be the mean weight of the burritos at this restaurant and ĉ be the mean weight of the burritos in the sample. Which of the following is an appropriate set of hypotheses for their significance test? Choose 1 answer:
A) H0 : x = 250 , Ha : x < 250
B) H0 : x = 250 , Ha : x > 250
C) H0 : μ = 250 , Ha: μ < 250
C) H0 : μ = 250 , Ha: μ > 250
Solution:
The null hypothesis is the hypothesis that is assumed to be true. The restaurant advertises that its burritos weigh 250. This is the null hypothesis. 250 is the population mean,μ . Thus, the null hypothesis is
H0 : μ = 250
The alternative hypothesis is what the researcher expects or predicts. The consumer advocacy group tests if the mean weight is significantly lower than 250g.
This is the alternative hypothesis. It is expressed as
H0 : μ < 250
Read more about test statistic here:
https://brainly.com/question/15110538
#SPJ1
What is the range of the relation? {(-4,1), (-2, 0), (8,-1)}
Answers
Answer:
The range of the relation is {1, 0, -1}.
Step-by-step explanation:
The range of a relation will be all the y-values in the ordered pairs.
add the following polynomial of x3+3xy-2×y2+y3,2×3-5x2y-3xy2-2y3
Answers
The addition of the polynomial \(x^{3}+3xy-2xy^{2} +y^{3}\) with \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\) is \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\).
What is a polynomial?
⇒ A polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables.
⇒ In the addition of polynomials, the like terms are added while in subtraction, the like terms are subtracted.
Calculation;
We have been given two polynomial which we have to add \(x^{3}+3xy-2xy^{2} +y^{3}\) and \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\)
The sign after addition or subtraction will always be of the variable having more value.
\((x^{3}+3xy-2xy^{2} +y^{3} )+(2x^{3}-5x^{2} y-3xy^{2}-2y^{3})\)
On adding like terms with each other
⇒ \((x^{3} +2x^{3})+ 3xy-5x^{2} y-(2xy^{2}+3xy^{2})+(y^{3}-2x^{3})\)
⇒ \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\)
Hence the addition of the polynomial\(x^{3}+3xy-2xy^{2} +y^{3}\) and \(2x^{3}-5x^{2} y-3xy^{2}-2y^{3}\) is \(3x^{3}+3xy-5x^{2} y-5xy^{2}-y^{3}\).
Learn more about polynomial here :
brainly.com/question/1487158
#SPJ9
Write the domain and range of the function represented below.
(2, 9), (3, 4), (-1, 2), (6, 1)
Domain:
Range:
Answers
Range: { 9 , 4 , 2 , 1 }
Domain is x
Range is y
the picture below shows the shape of a design painted on the side of a building. The design was formed by combining triangles and rectangles.
What is the area of the wall covered by the design?

Answers
Therefore , the solution of the given problem of surface area comes out to be 212 square feet of the wall are therefore covered by the design.
What exactly does an area mean?The total size of the object can be determined by calculating how much room would be required to completely cover its exterior. When choosing a similar product with a cylindrical form, the environment is taken into account. Anything's total dimensions are determined by its surface area. The amount of water that a cuboid can hold depends on the number of sides that link its four trapezoidal shapes.
Here,
We must first determine the area of each individual form before adding them together to determine the portion of the wall that the design covers.
Taking a look at the rectangle first, we can observe that it has the following area:
=> 120 square feet= 10 feet x 12 feet.
=> 40 square feet = (1/2)(10 ft)(8 ft).
Consequently, the two triangles' combined area is:
=> 80 square feet = 2 x 40 square feet.
=> (12 square feet) = (1/2)(6 ft)(4 ft).
The total area of all the shapes is as follows:
=> 212 square feet= 120 square feet, 80 square feet, and 12 square feet.
=> 212 square feet of the wall are therefore covered by the design.
To know more about surface area visit:
https://brainly.com/question/2835293
#SPJ1
Answer: the answer is 261 ^2 ft!
Step-by-step explanation:
just need help with part (b) please

Answers
In response to the stated question, we may state that As a result, the formula for the sequence's nth term is: \(a_n = a _1 * r^{(n-1) (n-1)}\)
What is Sequences?In mathematics, a sequence is an ordered list of items. Elements can be numbers, functions, or other mathematical objects. A series is commonly expressed by putting the phrases in parentheses and separating them with commas. A natural number series, for example, can be denoted as: (1, 2, 3, 4, 5, ...) Similarly, the even number series is labelled as follows: (2, 4, 6, 8, 10, ...) A series can be finite or infinite depending on whether it has a finite or infinite number of words.
a. Since the difference between subsequent terms is constant, the series 5, 7, 8,... is an arithmetic sequence. The usual difference is 2, specifically. As a result, the formula for the sequence's nth term is:
\(a_n = a_1 + (n-1)d\)
where a 1 represents the first term, d represents the common difference, and n represents the term number. Using the provided values, we get:
\(a_n = 5 + (n-1)2\\a_n = 2n + 3\)
b. Since the ratio between subsequent terms is constant, the series 6, 30, 150,... is a geometric sequence. The common ratio is 5, specifically. As a result, the formula for the sequence's nth term is:
\(a_n = a _1 * r^{(n-1) (n-1)}\)
where a 1 denotes the first term, r the common ratio, and n the term number
\(a_n = 6 * 5^{(n-1) (n-1)}\)
To know more about Sequences visit:
https://brainly.com/question/21961097
#SPJ1
URGENT!!!!!
math assignment(not to be confused with assessment) that I need help with

Answers
The statements that are true in the lines of construction of the straightedge and compass construction which makes use of congruent circles, are;
Line EF is the perpendicular bisector of segment BD
Line EF is the bisector of angle BAC
How are a compass and straightedge used to construct geometric figures?Geometric figures are constructed using a compass and a straightedge, by using outlined steps or procedures.
From the diagram, given that the circumference of the circle with center B passes through the center of the circle with center D, and vice versa, we have;
Circle B is congruent to circle D
Construction of Perpendicular Bisector to Line BDThe steps to construct a perpendicular bisector to the segment BD includes;
Placing the compass at point B and draw an arc above and below segment BC then place the compass at point D then draw arcs above and below the segment BD to intersect the previous arcs drawn from point B. at points E and FJoin the point of intersection of the two arcs which are the points E and F to complete the the construction of the perpendicular bisector of segment BDTherefore;
Line EF is the perpendicular bisector of segment BDThe steps to construct the angle bisector of angle BAC
The angle bisector can be constructed by using the following steps
Place the compass at point A which is the vertex of the angle, and draw arcs to intersect the arms of the angle at B and D Place the compass at points B and D and draw arcs above BD to intersect at point F which is on the of BD away from point AJoin FAV to complete the construction of the bisector of angle BACWhich gives;
Line EF is the bisector of angle BACLearn more about construction of geometric figures here:
https://brainly.com/question/17834363
#SPJ1
population has decreased by 30% in the past A city has a population of 350,000. The ten years. What was the population of the city ten years ago?
Answers
Answer:
the population used to be 455,000
Step-by-step explanation:
Consider the function f(x) = x2 - 4x + 8 on the interval 0, 4. Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0. Find all such values c and enter them as a comma-separated list. Values of c =: (1 point) Consider the function graphed below. P n ? Does this function satisfy the hypotheses of the Mean Value Theorem on the interval a, b ? Does it satisfy the conclusion?? f(b) f(a)2 At what point c is f'(c) b - a
Answers
Verifying that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c = 2 such that f'(c) = 0.
Given:
Consider the function f(x) = x2 - 4x + 8 on the interval 0, 4. Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0.
f(x)=x^2−4x+8, [0,4]
when, x = 0
f(x) = x^2 -4x +8
f(0) = y = 0 - 0 + 8 = 8
when, x=4
f(5) = y = 16 - 16+8 =
thus, we have 2 points (0, 8) ; (4, 8)
slope,m = {8-(8)} / {4-0} = 0
hence, we have to calculate all the points,x where 0<x<8 and slope=0
f '(x) = 2x - 4 = 0
or, f '(c) = 2c - 4 = 0
c = 4/2 =2 ( 0<x<4)
hence, the there is only one solution c=2 which satisfies Rolle's theorem.
Learn more about the rolle's theorem here:
https://brainly.com/question/13972986
#SPJ4
Can someone please help me find out the valu of X?

Answers
To determine the value of x, you have to apply the Thales theorem. Which states that the line segments determined by the parallel lines are at the same ratio, so that:
\(\frac{x}{28}=\frac{8}{16}\)From this expression, you can determine the value of x. Multiply both sides f the equal sign by 28 to calculate the value of x:
\(\begin{gathered} 28\cdot\frac{x}{28}=28\cdot\frac{8}{16} \\ x=14 \end{gathered}\)The value of x is equal to 14
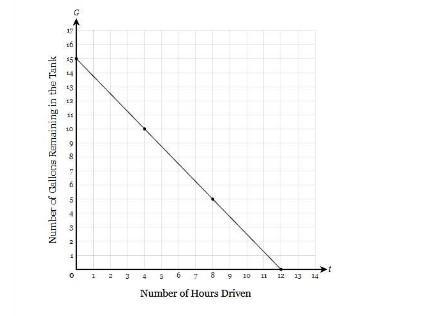
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
Write the product using exponents.
(−7) (−7) (−7) (−7) (−7) (−7) (−7) (−7)
Answers
Answer:
(-7)^8
Step-by-step explanation:
You write as (-7) to the power of n where n is the #of times you write (-7)
Answer:
-7
Step-by-step explanation:
Unit 8 homework 2 special right triangles
Answers
Two square floor tiles are made of the same material.One costs 180 naira and its edge is 30cm long.Find the cost of the other if its edge is 50cm long
Answers
Answer:
300 naira
Step-by-step explanation:
Steps to answer this question
we have to first determine the cost per cm the answer gotten is then multiplied by 50cmcost per cm = 180 /30 = 6 naira
cost of the other edge = 6 naira x 50 = 300 naira
There is a line whose slope is 7 and whose y-intercept is 9. What is its equation in slope-intercept form?
Answers
Answer:
Y=7x+9
Step-by-step explanation:
Y=mx + b
b= y-intercept
m=slope
Substitute:
Y=7x+9
The yearly depreciation rate for a car is modeled by r = 1 - (V/C)^1/n, where V'is the value of the car after n years, and C'is the original cost. (a) Determine the depreciation rate for a car that originally cost S20,000 and is worth $12,000 after 4 yr. Round to the nearest tenth of a percent. (b) Determine the original cost of a car that has a yearly depreciation rate of 11% and is worth $10,000 after 2 yr. Round to the nearest S100 Part 1 of 2 (a) The depreciation rate is approximately __ % per year. Round to the nearest tenth of a percent. Part 2 of 2 (b) The original cost of a car is approximately $ __ Round to the nearest S100.
Answers
(a) The depreciation rate for the car is approximately 16.6% per year. (b) The original cost of the car is approximately $18,200.
(a) The depreciation rate for the car is approximately 16.6% per year. (b) The original cost of the car is approximately $18,200.
To find the depreciation rate in part (a), we can use the formula r = 1 - (V/C)^1/n, where V = $12,000, C = $20,000, and n = 4. Plugging these values in, we get r = 1 - (12,000/20,000)^(1/4) ≈ 0.166, or 16.6% rounded to the nearest tenth of a percent.
To find the original cost of the car in part (b), we can use the formula V = C(1 - r)^n, where V = $10,000, r = 0.11, and n = 2. Solving for C, we get C = V / (1 - r)^n = 10,000 / (1 - 0.11)^2 ≈ 18,200, rounded to the nearest $100.
To know more about depreciation rate, refer here:
https://brainly.com/question/30531944#
#SPJ11
Simplify the expression. sin^2 Ø/ csc Øtan^2 Ø

Answers
Answer: OPTION (B): sin θ cos^2 θ
Therefore, The simplified expression is OPTION (B): sin θ cos^2 θ,
Which corresponds to:
sin^2 θ / csc θtan^2 θ is OPTION (B): sin θ cos^2 θ,
Step-by-step explanation:Rewrite In Terms of SINE and COSINE:
sin^2 θ / 1 / sinθ * sin^2 θ / cos^2 θ
Simplify the Denominator:sin^2 θ / sin^3 θ / cos^2 θ
Multiply by the Reciprocal:sin^2 θ * cos^2 θ / sin^3 θ
Cancel out the Common Factors:sin^2 θ * cos^2 θ / sin^3 θ = sin θ * cos^2 θ / sin^2 θ
Cancel sin θ from Numerator and Denominator:sin θ * cos^2 θ / sin^2 θ = sin θ cos^2 θ
Draw the Conclusion: Match with the given options:Therefore, Therefore, The simplified expression is
OPTION (B): sin θ cos^2 θ,
Which corresponds to:sin^2 θ / csc θtan^2 θ is OPTION (B): sin θ cos^2 θ,
I hope this helps you!
the edges of a cube increase at a rate of 2 centimeters per second. how fast is the volume changing when the length of each cube edge is 50 centimeters ?
Answers
The required volume of the cube is increasing at a rate of 15,000 cubic centimeters per second when the length of each edge is 50 centimeters and the edges are increasing at a rate of 2 centimeters per second.
Let us consider V be the volume of the cube,
And s be the length of one edge of the cube.
Volume of a cube is equal to,
V = s^3
To find how fast the volume is changing with respect to time,
Use the chain rule of differentiation,
dV/dt = dV/ds × ds/dt
where dV/dt is the rate of change of volume with respect to time,
dV/ds is the rate of change of volume with respect to the length of one edge of the cube,
And ds/dt is the rate of change of the length of one edge of the cube with respect to time.
ds/dt = 2 cm/s,
find dV/dt when s = 50 cm.
First, find dV/ds,
dV/ds = 3s^2
Then, we can plug in s = 50 cm,
dV/ds = 3(50)^2
= 7500 cm^2
Finally, we can plug in the values we have to find dV/dt,
dV/dt = (dV/ds) × (ds/dt)
= 7500 cm^2/s × 2 cm/s
= 15,000 cm^3/s
Therefore, the volume of the cube is increasing at a rate of 15,000 cubic centimeters per second .
Learn more about volume here
brainly.com/question/20066234
#SPJ4