1
2
3
4
5
6
10
34:10
Which division problem does the model show?
1
1
1
1
1
3
3-3 -9
9
San

Answers
Answer:
3 ÷ 1/3 = 9
Step-by-step explanation:
= 3 ÷ 1/3
= 3/3 (3/1) ÷ 1/3
= 9/3 × 3/1
= 9/1
= 9
Related Questions
A group of 500 middle school students were randomly selected and asked about their preferred television genre. A circle graph was created from the data collected.
a circle graph titled preferred television genre, with five sections labeled drama 14 percent, sports, documentaries 24 percent, reality 20 percent, and sci-fi 20 percent
How many middle school students prefer the Sports television genre?
22
78
79.2
110
Answers
Answer:
110 students
Step-by-step explanation:
The total is 100%. Subtract the other parts of the circle to find the percent for sports.
100 - 14 -24-20 -20
22
Sports is 22%
Multiply the number of students by the percentage of students that prefer sports
500 *22%
500 *.22
110
Answer: 110 students
42 + z= 131
what is z?
Answers
Answer:
z=89
Step-by-step explanation:
42+z=131
take 42 away from both sides
z= 89
Answer:
z = 89
Step-by-step explanation:
42 + z = 131
z = 131 - 42
z = 89
A club raised 175% of its goal for a charity. The club raised $763. What was the goal?
Answers
Answer: The clubs goal is to raise $436.
Step-by-step explanation:
175% * x = 763 where x is the goal
1.75 *x = 763
1.75x = 763
x= 436
\(\$436\)
A percentage is a number or ratio expressed as a fraction of \(\boldsymbol{100}\)
Percentage of amount raised for charity \(=175\%\)
Amount raised for charity \(=\$763\)
Therefore,
\(175\%\) of amount of goal \(=\$763\)
\(\frac{175}{100}\times \) Amount of goal \(=\$763\)
Amount of goal \(=\frac{76300}{175} \)
\(=\boldsymbol{\$436}\)
For more information:
https://brainly.com/question/2724587?referrer=searchResults
Edwin sells jars of jam for $1.90 each. Determine how many jars of jam Edwin needs to sell to break even if the variable cost per jar is $1.10 and fixed expenses are $35,700.00 per year.
Answers
Edwin needs to sell 44,625 jars of jam to break even.
To determine how many jars of jam Edwin needs to sell to break even, we'll calculate the breakeven point using the following formula:
Breakeven Point = Fixed Expenses / (Selling Price per Unit - Variable Cost per Unit)
Given information:
Selling Price per Unit (SP) = $1.90
Variable Cost per Unit (VC) = $1.10
Fixed Expenses = $35,700.00 per year
Plugging in the values into the formula:
Breakeven Point = $35,700 / ($1.90 - $1.10)
Breakeven Point = $35,700 / $0.80
Breakeven Point = 44,625 jars
Therefore, Edwin needs to sell 44,625 jars of jam to break even.
for such more question on breakeven point
https://brainly.com/question/30551452
#SPJ8
Wind and Moisture: To understand how weather and landscape affect the spread of wildfires, an experiment was conducted in a low velocity wind tunnel. A fire was started in pine litter, and the researchers measured the fire spread rate for varying wind speeds and pine litter moisture contents. Data for fires started in pine litter that had a moisture content of 4% are shown in the table below.
Answers
Based on the scatterplot, the form of the relationshipbetween fire spread rate and wind speed can be described as a positive correlation.
How is this so?As wind speed increases,the fire spread rate also tends to increase.
b. Direction -
Based on the given scatterplot,the direction of the relationship between fire spread rate and wind speed appears to be positive.
As the wind speed increases,the fire spread rate generally tends to increase as well.
c. Strength -
The scatterplot suggests a moderate to strong relationship between fire spread rate and wind speed.
The data points exhibit a somewhat linear pattern, indicating that there is a noticeable association between these variables.
The firespread rate tends to increase consistently as the wind speed increases, suggesting a relatively strong positive correlation between the two factors.
Learn more about correlation at:
https://brainly.com/question/13879362
#SPJ1
Full Question:
Wind and Moisture: To understand how weather and landscape affect the spread of wildfires, an experiment was conducted in a low velocity wind tunnel. A fire was started in pine litter, and the researchers measured the fire spread rate for varying wind speeds and pine litter moisture contents.
Data for fires started in pine litter that had a moisture content of 4% are shown in the table below.
Wind Speed (miles/hour) Fire Spread Rate (feet/minute)
0.76 0
1.78 2
3.34 4
5.38 6
8.10 8
11.75 10
16.70 12
A scatterplot of these data is shown here -
1. Based on the scatterplot, how would you describe the following with regard to the relationship between fire spread rate and wind speed?
a. Form:
b. Direction:
c. Strength:

A rainwater collection system uses a cylindrical storage tank with a diameter of 50 cm and a height of 80 cm what is the total volume of water in cubic centimeters that can be collected
Answers
Answer:
157,000
Step-by-step explanation:
π r² h
the three data sets show the number of text messages sent by jada, and diego, and lin over 6 days. one of the data sets has a mean of 4, one has a mean of 5, and one has a mean of 6.
1. which data set has which mean? what does this tell you about the text messages sent by the three students?
2. which data set has the greatest variabillity? Explain
Answers
1. Jada's data set has a mean of 5, Diego's data set has a mean of 6, and Lin's data set has a mean of 4.
2. The data set that has the greatest variability is Lin's data set because it has the highest standard deviation of 3.6.
How to calculate the mean for the set of data?In Mathematics and Geometry, the mean for this set of data can be calculated by using the following formula:
Mean = [F(x)]/n
Question 1.
In this scenario and exercise, we would determine the mean of the three data sets based on the number of text messages sent by Jada, and Diego, and Lin over 6 days as follows;
Mean number of text for Jada = (4 + 4 + 4 + 6 + 6 + 6)/6
Mean number of text for Jada = 30/6
Mean number of text for Jada = 5.
Mean number of text for Diego = (4 + 5 + 5 + 6 + 8 + 8)/6
Mean number of text for Diego = 36/6
Mean number of text for Diego = 6.
Mean number of text for Lin = (1 + 1 + 2 + 2 + 9 + 9)/6
Mean number of text for Lin = 24/6
Mean number of text for Lin = 4.
Question 2.
In Statistics, variability is a measure of the spread of a data set. Also, we would use standard deviation to determine the variability in each data set as follows;
Standard deviation = √(1/n × ∑(xi - u₁)²)
Standard deviation for Jada = √(1/6 × [(4 - 5)² + (4 - 5)² + (4 - 5)² + (6 - 5)² + (6 - 5)² + (6 - 5)²]
Standard deviation for Jada = √(6/6) = 1
Standard deviation for Diego = √(1/6 × [(4 - 6)² + (5 - 6)² + (5 - 6)² + (6 - 6)² + (8 - 6)² + (8 - 6)²]
Standard deviation for Diego = √(14/6) = 1.53
Standard deviation for Lin = √(1/6 × [(1 - 4)² + (1 - 4)² + (2 - 4)² + (2 - 4)² + (9 - 4)² + (9 - 4)²]
Standard deviation for Lin = √(76/6) = 3.6
Read more on mean here: brainly.com/question/9550536
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Suppose that the scores of a standardized test are normally distributed with an unknown mean and standard deviation. A random sample of 21 scores is taken and gives a sample mean of 95 points and a sample standard deviation of 8 points.
df t0.10 t0.05 t0.025 t0.01 t0.005
17 1.333 1.740 2.110 2.567 2.898
18 1.330 1.734 2.101 2.552 2.878
19 1.328 1.729 2.093 2.539 2.861
20 1.325 1.725 2.086 2.528 2.845
21 1.323 1.721 2.080 2.518 2.831
Find the margin of error for a 95% confidence interval estimate for the population mean using the Student's t-distribution
Use the portion of the table above. Round the final answer to two decimal places.
Provide your answer below:
ME = _______.
Answers
Answer:
ME = 3.64
Step-by-step explanation:
Given:
Sample size, n = 21
Sample mean, X' = 95
Standard deviation \( \sigma \) = 8.
Confidence interval = 95%
Significance level \( \alpha\) = 0.05
Required:
Find margin of error
To find the margin of error, use the formula below:
\( M.E = \frac{\sigma}{\sqrt{n}} * t_\alpha_/_2; _d_f \)
Where,
\( t_\alpha_/_2 = 0.05/2 = 0.025\)
degree of freedom, df = n - 1 = 21 - 1 = 20
Therefore,
\( M.E = \frac{8}{\sqrt{21}} * t_0_._0_2_5; _2_0 \)
Using the table at 95% Confidence interval, we have:
\( = \frac{8}{\sqrt{21}} * 2.086 \)
\( = 3.6416 \)
Rounding to 2 decimal places,
ME = 3.64
Help me please i'm stuck on this question!!
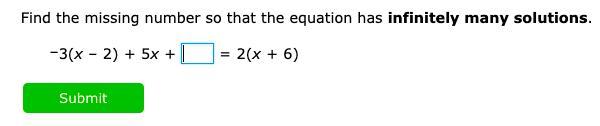
Answers
The missing number so that the equation has infinitely many solutions is 6
For the given equation to have an infinite number of questions, the value of x must be an infinite value.
Given the expression -3(x-2) + 5x + y = 2(x + 6)
Expand the equation
-3x + 6 + 5x + y = 2x + 12
2x + (6 + y) = 2x + 12
For the equation to have infinitely many solutions, 6+y must be equal to 12, that is 6+y = 12
y = 12 - 6
y = 6
Hence the missing number so that the equation has infinitely many solutions is 6
Learn more here; https://brainly.com/question/11966980
The missing number so that the equation has infinitely many solutions is 6.
An equality has infinitely many solutions if it is an identity, that is, both sides are equal.
In this problem, the equality is:
\(-3(x - 2) + 5x + v = 2(x + 6)\)
\(-3x + 6 + 5x + v = 2x + 12\)
\(2x + 6 + v = 2x + 12\)
\(6 + v = 12\)
\(v = 12 - 6\)
\(v = 6\)
The missing number is 6.
A similar problem is given at https://brainly.com/question/14535990
Some values of functions f, g, h, and k are provided in the table on the right.
Find a possible equation of each function Verify your results with a graphing
calculator table. (HINT Use linear or exponential equations]
The equation of function f is f(x) =?

Answers
Without any values of the functions f, g, h, and k, it is not possible to find the equation of each function. The equation of a function can be determined by analyzing the values of the function. Based on the given values, a possible equation can be found and then verified by plotting the points on a graph and seeing if they align with the equation.
It's important to note that the equation can be a linear or exponential equation but it's impossible to determine it without any values.
What is 1400 x 3278
i need help
Answers
Answer:
4,589,200
Step-by-step explanation:
Answer:
4589200
Step-by-step explanation:
hope this helps!! :D
A cubic root function has a domain of x≥−3 and a range of y≥−1. What is the range of its inverse?
Answers
In general, if the range of a function is y≥−1, its inverse has a domain of y≥−1. So, the range of the inverse of the cubic root function is y≥−1.
How do we know this?The range of a cubic root function becomes the domain of a cube function and vice versa since a cubic root function is an inverse function of a cube function. Therefore, the cube function's range is x3 if the cubic root function's domain is x3.
A function's inverse typically has a domain of y1 if its range is y1. Therefore, y1 is the domain of the inverse of the cubic root function.
Describe a function.
A function is a mathematical relationship between a domain—a set of inputs—and a range—a set of outputs. Each input in the domain is given a distinct output, known as the function value, by a function. An equation or graph can be used to depict the function value.
A function is typically represented symbolically by an equation that describes the relationship between the inputs and outputs and a letter, like f or g, as well as the letter. For instance, the equation of a function that accepts a value of x as input and produces its square is f(x) = x2.
Learn more about Functions here
https://brainly.com/question/17043948
#SPJ1
What is \(lim_{x-0} (f(f(x))\) closest to?
a. DNE
b. 1
c. 3
d. 5
![What is [tex]lim_{x-0} (f(f(x))[/tex] closest to?a. DNEb. 1c. 3d. 5](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/NmXWvSXkdO4pcmJwPPMurvHaNHVvCNFQ.jpeg)
Answers
Answer:
c. 3
Step-by-step explanation:
You want to know the limit of the composite function f(f(x)) as x approaches zero.
LimitThe function f(x) can be evaluated at x=0. The graph shows the value to be ...
f(0) = 2
The function f(x) can also be evaluated at x=2. The graph shows the value to be ...
f(2) ≈ 3
The nearest value to f(f(0)) is 3.
__
Additional comment
For a continuous function, the limit at a point is simply the value at that point. F(x) is continuous in the neighborhoods of the points of interest, so we simply need to find the function value.
Find the equation of the line below

Answers
look at this system of exquations. y=2x-1 4x +y=2 which shows a correct step using substitution to solve the system of equations?
Answers
The solution to the system of equations is x = 0.5, y = 0
How to solve the system of equations?The system of equations is given as:
y = 2x-1
4x + y=2
Substitute y = 2x-1 in 4x + y=2
4x + 2x-1 =2
Evaluate the like terms
6x = 3
Divide by 6
x = 0.5
Substitute x = 0.5 in y = 2x-1
y = 2 * 0.5 - 1
Evaluate
y = 0
Hence, the solution to the system of equations is x = 0.5, y = 0
Read more about system of equations at:
https://brainly.com/question/13729904
#SPJ1
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
Will mark brainiest for CORRECT answer!

Answers
ANSWER: y = (1/2)x - 1.
To find the equation of the tangent line to the curve y = √(x - 3) at the point (4, 1), we need to determine the slope of the tangent line and its y-intercept.
First, let's find the derivative of the function y = √(x - 3) using the power rule:
dy/dx = 1/(2√(x - 3))
Now, we can substitute x = 4 into the derivative to find the slope of the tangent line at that point:
m = dy/dx = 1/(2√(4 - 3)) = 1/2
So, the slope of the tangent line is 1/2.
Next, we can use the point-slope form of a line to find the equation of the tangent line. Given the point (4, 1) and the slope m = 1/2, the equation becomes:
y - y1 = m(x - x1)
Substituting the values (x1, y1) = (4, 1):
y - 1 = (1/2)(x - 4)
Simplifying the equation:
y - 1 = (1/2)x - 2
y = (1/2)x - 1
Therefore, the equation of the tangent line to the curve y = √(x - 3) at the point (4, 1) is y = (1/2)x - 1.
Answer:
y = (1/2)x - 1/2
Step-by-step explanation:
Step 1: Find the derivative of the function
The derivative of a function gives the slope of the tangent line to the curve at any point. To find the derivative of the given function y = sqrt(x - 3), we can use the power rule of differentiation which states that:
d/dx (x^n) = nx^(n-1)
Applying this rule to our function, we get:
dy/dx = d/dx sqrt(x - 3)
To differentiate the square root function, we can use the chain rule of differentiation which states that:
d/dx f(g(x)) = f'(g(x)) * g'(x)
Applying this rule to our function, we have:
g(x) = x - 3
f(g) = sqrt(g)
So,
dy/dx = d/dx sqrt(x - 3) = f'(g(x)) * g'(x) = 1/(2*sqrt(g(x))) * 1
Substituting g(x) = x - 3, we get:
dy/dx = 1/(2*sqrt(x - 3))
So, the derivative of y with respect to x is 1/(2*sqrt(x - 3)).
Step 2: Evaluate the derivative at the given point
To find the slope of the tangent line at the point (4, 1), we need to substitute x = 4 into the derivative expression:
dy/dx = 1/(2*sqrt(4 - 3)) = 1/2
So, the slope of the tangent line at the point (4, 1) is 1/2.
Step 3: Use point-slope form to write the equation of the tangent line
Now that we know the slope of the tangent line at the point (4, 1), we can use point-slope form to write the equation of the tangent line. The point-slope form of a line is given by:
y - y1 = m(x - x1)
where (x1, y1) is the point on the line and m is the slope of the line.
Substituting the values x1 = 4, y1 = 1, and m = 1/2, we get:
y - 1 = (1/2)*(x - 4)
Simplifying this equation, we get:
y = (1/2)x - 1/2
So, the equation of the tangent line to the curve y = sqrt(x - 3) at the point (4, 1) is y = (1/2)x - 1/2.
Hope this helps!
3. Rhombus KLMN with vertices K(-3, 2), L(1, 4),
and N(-5, -2): (x,y) → (x+2, y-5)
Answers
The translated vertices of the rhombus are: K(-1,-3), L(3,-1), M(1,-5) and N(-3,-7)
The rhombus is a parallelogram which has all sides equal. the diagonals of a rhombus bisect at right angles. the difference between a rhombus and a square is that none of the angles of a rhombus are 90°.
To translate a figure with given co-ordinates into another figure with a particular translation we simply add or subtract the given values from the coordinates of the available points.
Given co-ordinates of Rhombus are K(-3, 2),L(1, 4),M(-1 ,0)and N(-5, -2).
The translation is given as (x,y) → (x+2, y-5)
So we calculate the coordinates as:
The translated co-ordinate K(-3, 2)→ K'(-1,-3)
The translated co-ordinate L(1, 4)→ L'(3,-1)
The translated co-ordinate M(-1 ,0)→ M'(1,-5)
The translated co-ordinate N(-5, -2)→ N'(-3,-7)
Hence the co-ordinates of rhombus translated by (x,y) → (x+2, y-5) are K(-1,-3), L(3,-1), M(1,-5) and N(-3,-7).
To learn more about Rhombus visit:
https://brainly.com/question/27870968
#SPJ9
Differentiate y=x4 -x
Answers
Answer:
Step-by-step explanation:
To differentiate the function y = x^4 - x, we will use the power rule of differentiation. The power rule states that if f(x) = x^n, then the derivative of f(x) is f'(x) = nx^(n-1).
So, for y = x^4 - x, we can find the derivative as follows:
y' = 4x^3 - 1
So, the derivative of the function y = x^4 - x is y' = 4x^3 - 1.
A beach volleyball court is 8 meters wide and 17 meters long. The rope used for theboundary line costs $1.00 per meter. How much would it cost to buy a new boundary line forthe court?
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
A beach volleyball court is 8 meters wide and 17 meters long.
The rope used for the boundary line costs $1.00 per meter.
How much would it cost to buy a new boundary line for
the court?
Step 2:
The details of the solution are as follows:
Since the beach volleyball is 8 meters wide and 17 meters long.
Then, the boundary line ( perimeter ) =
\(\begin{gathered} =2\text{ \lparen 8 + 17 \rparen} \\ =\text{ 2 x 25} \\ =\text{ 50 meters} \end{gathered}\)The rope used for the boundary line costs $1.00 per meter.
\(\begin{gathered} \text{ \$ 1. 00 = 1 meter} \\ Then,\text{ we have that:} \\ \text{ \$ 50. 00 = 50 meters} \end{gathered}\)CONCLUSION:
The final answer is:
\(\text{ \$ 50 . 00}\)1 a) A restaurant is open 24 hours a day. The manager wants to divide the day into work shifts of equal length. The shifts w=should not overlap. All shifts durations should be a whole number of hours. Describe the different ways this can be done.
b) The manager turns on the restaurant's two neon signs at the same time. Both signs blink as they are turned o. One blinks every 9 seconds. The other sign blinks every 15 seconds. In how many seconds will they blink together again?
Answers
The possible answers for the restaurants are Three 8-hour shifts; four 6-hour shifts; six 4-hour shifts.
2. The seconds that they will blink together again is 45 seconds.
How to illustrate the information?Here we have to determine the factors of 24 for the shifts i.e. 1, 2, 3, 4, 6, 8, 12, 24 .
A 1-hour shift does not make much sense; most employers will also not use a 2-hour or 3-hour shift.
Restaurants typically do not use 12-hour shifts either, and employers do not use 24-hour shifts either.
Since both signs blink as they are turned on and one blinks every 9 seconds. The other sign blinks every 15 seconds. The least common multiple is 45.
Learn more about restaurant on:
https://brainly.com/question/546180
#SPJ1
Todd rolled a 12-sided die marked with the numbers 1 to 12. These are his experimental probabilities.
P(odd number) = 18/48
P(greater than 8) = 16/48
P(9) = 12/48
1. Which experimental probability matches the theoretical probability exactly?
2. Which experimental probability is farthest from the theoretical probability?
Answers
The experimental probability farthest from the theoretical probability is P(greater than 8). The theoretical probability of rolling a 9 is 1/12 because there is one 9 out of twelve total possible outcomes.
Experimental probability refers to the probability of an event based on data acquired from repeated trials or experiments.
Theoretical probability is the probability of an event occurring based on logical reasoning or prior knowledge. In Todd’s case, he rolled a 12-sided die marked with the numbers 1 to 12.
The probabilities are as follows:P(odd number) = 18/48P(greater than 8) = 16/48P(9) = 12/48To answer the questions:1. Which experimental probability matches the theoretical probability exactly?The theoretical probability of rolling an odd number is 6/12 or 1/2 because there are six odd numbers out of the twelve total possible outcomes.
The experimental probability Todd obtained was 18/48. Simplifying 18/48 to lowest terms gives 3/8, which is equal to 1/2, the theoretical probability.
Therefore, the experimental probability that matches the theoretical probability exactly is P(odd number).2. Which experimental probability is farthest from the theoretical probability? The theoretical probability of rolling a number greater than 8 is 3/12 or 1/4 because there are three numbers greater than 8 out of twelve total possible outcomes.
The experimental probability Todd obtained was 16/48. Simplifying 16/48 to lowest terms gives 1/3, which is not equal to 1/4, the theoretical probability.
The experimental probability Todd obtained was 12/48. Simplifying 12/48 to lowest terms gives 1/4, which is not equal to 1/12, the theoretical probability.
However, the difference between the experimental probability and the theoretical probability for P(9) is smaller than that of P(greater than 8). Therefore, P(greater than 8) is the experimental probability that is farthest from the theoretical probability.
For more such questions on possible outcomes
https://brainly.com/question/30241901
#SPJ8
An ecologist finds 220 yellow-flowered plants and 180 white-flowered plants. Use the normal distribution to find the Lower boundary of a 95% confidence interval for the proportion of yellow-flowered plants. Which of the following answers is correct to 2 decimal places?
a. Lower boundary = 0.30
b. Lower boundary = 0.60
c. Lower boundary = 0.50
d. Lower boundary = 0.40
Answers
Answer:
c. Lower boundary = 0.50
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
An ecologist finds 220 yellow-flowered plants and 180 white-flowered plants.
220 out of 220 + 180 = 400. So
\(n = 400, \pi = \frac{220}{400} = 0.55\)
95% confidence level
So \(\alpha = 0.05\), z is the value of Z that has a p-value of \(1 - \frac{0.05}{2} = 0.975\), so \(Z = 1.96\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.55 - 1.96\sqrt{\frac{0.55*0.45}{400}} = 0.5\)
Thus the correct answer is given by option c.
choose all the ones
Bella is taking classes at her local gym where a few pricing choices are available to her. She wants her average cost for each class to be below $6 per class. Which pricing choice has an average price less than $6 per class?
Choose all that are correct.
A.
$196 for 35 classes
B.
40-class pass for $260
C.
50-class pass for $250
D.
10-class pass for $55
E.
$342 for 45 classes
Answers
Answer:
A, C, D
Step-by-step explanation:
A. $5.60 per class
$196 divided by 35
B. $6.50 per class
$260 divided by 40
C. $5.00 per class
$250 divided by 50
D. $5.50 per class
$55 divided by 10
E. $7.60 per class
$342 divided by 45
avg price for B = $260/40 = $6.50
avg price for C = $250/50 = $5
avg price for D = $55/10 = $5.50
avg price for E = $342/45 = $7.60
answer : A,C,D
Hello,Can you please help me with question# 11 ? it is express each sum using summation notation. Use 'i' as the index of th sum

Answers
Given:
The sum of terms
\(4^3+5^3+6^3..........+13^3\)Required:
Find sum.
Explanation:
We know sum of cube of first n terms of natural numbers
\(\sum_{n\mathop{=}1}^{\infty}n^3=[\frac{n(n+1)}{2}]^2\)Now,
\(\begin{gathered} =(1^3+2^3+....+13^3)-(1^3+2^3+3^3) \\ =[\frac{13(13+1)}{2}]^2-36 \\ =8281-36 \\ =8245 \end{gathered}\)Answer:
The sum of terms is 8245.
Which equation is represented by the graph below?
Chose from:
y = e^x
y = e^x - 1
y = ln x
y = ln x - 1

Answers
Answer:
attached
Step-by-step explanation:
y = ln (x)

During a heavy storm rain falls for 4.1 hours through the night. A weather station monitors the rain by measuring the milliliter of water it takes to fill a container . How many milliliters of rain will fill the container of the rain falls at a rate of 4 quarts per 25 minutes?
Answers
Answer:
37240.3 mlStep-by-step explanation:
1 quart = 946 ml4 quarts per 25 minutes to be converted into ml per hour
4 quarts per 25/60 hr = ⇒ quarts to ml, minutes to hour4*946 ml per 0.4166 hr =3784 ml per 0.4166 hr =3784/0.4166 ml per 1 hr = ⇒ volume per hour9083 ml/hrFor the time of 4.1 hr the volume of rain water is:
9083*4.1 ml = 37240.3 mlRichard bought 3 slices of cheese pizza and 2 sodas for $8.75. Jordan bought 2 slices of cheese pizza and 4
sodas for $8.50. How much would an order of slice of cheese pizza and 3 sodas cost? 3
O $3.25
• $5.25
• $7.75
• $17.25
Answers
Cost of 1 slice of pizza and 3 sodas = $5.25
What is Linear Programming?When the requirements of a mathematical model are represented by linear relationships, the best result can be obtained using a technique known as linear programming (LP), also known as linear optimization. A particular type of mathematical programming is linear programming. Formally speaking, linear programming is a method for optimising a linear objective function under the constraints of linear equality as well as linear inequality. Convex polytopes, a set defined as that of the intersection of a finite number of half spaces, which are defined by a linear inequality, make up its feasible region. A real-valued affine (linear) function defined on the this polyhedron serves as its objective function. If there is a point in the polytope in which this function does have the smallest (or largest) value, a linear programming algorithm locates it.
Let the cost of 1 slice of pizza be x and cost of 1 soda be y.
Now,
Richard bought 3 slices of pizza and 2 sodas for $8.75
Therefore, \(3x+2y=8.75\)
Jordan bought 2 slices of pizza and 4 sodas for $8.50
Therefore, \(2x+4y=8.50\)
Solving above equations, we get \(x=2.25\) and \(y= 1\).
Cost of 1 slice of pizza and 3 sodas = 2.25 + 3*1
= 2.25 + 3
= 5.25
Hence, Cost of 1 slice of pizza and 3 sodas = $5.25
Learn more about Linear Programming from the link.
https://brainly.com/question/14309521
#SPJ2
The question is below the screen

Answers
9514 1404 393
Answer:
x = 12
Step-by-step explanation:
The square of the length of the tangent segment is equal to the product of lengths from the external common point to the two circle intersections of the secant.
x^2 = (2)(70+2)
x^2 = 144
x = √144
x = 12
Find the sample size needed so that a 99.5% confidence interval will have margin of error of 1.5.

Answers
Keep in mind that without the population standard deviation, it is impossible to provide an exact sample size. However, this formula will give you a good starting point.
To find the sample size needed for a 99.5% confidence interval with a margin of error of 1.5, we can use the formula:
n = (Z * σ / E)^2
where n is the sample size, Z is the Z-score corresponding to the desired confidence level, σ is the population standard deviation, and E is the margin of error.
For a 99.5% confidence interval, the Z-score is approximately 2.807 (from a standard normal distribution table). Since we do not have the population standard deviation (σ), we will need to estimate it using a sample standard deviation or use a conservative approach by assuming the maximum possible value. For now, let's assume we have an estimated standard deviation.
n = (2.807 * σ / 1.5)^2
Solve for n by plugging in the estimated standard deviation (σ) and then round up to the nearest whole number, as you cannot have a fraction of a sample.
To learn more about : formula
https://brainly.com/question/29797709
#SPJ11