2, 2, 2, 3, 4, 4, 11
What is the median of the seven data values shown?
Answers
Answer:
Median is 3
Step-by-step explanation:
Related Questions
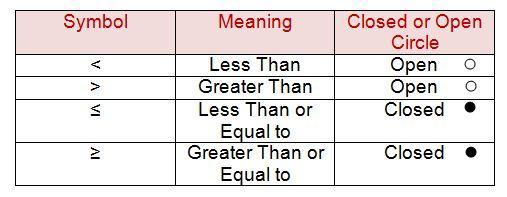
Solve the inequality and graph the solution on the number line.
h−9 ≤ 3
I couldn't screenshot the graph
Answers
Answer:
A closed circle on 12, going to the left.
Step-by-step explanation:
h − 9 ≤ 3
+ 9 + 9
h ≤ 12
Look for a closed circle on 12, going to the left.
Hope that helps!
) what is the probability that a pc is in a bedroom? (b) what is the probability that it is not in a bedroom? (c) suppose a household is selected at random from households with a pc; in what room would you expect to find a pc?
Answers
The answer is a) The probability is 0.32 ; b)The probability is 0.68 ; and c) Office or den.
a) The probability that a PC is in a bedroom is the sum of the probabilities of a PC being is an adult bedroom, child bedroom or other bedroom:
\(P_{bedroom} = P_{adult} +P_{child}+P_{other}\)
\(P_{bedroom}\) = 0.03 + 0.15 + 0.14
\(P_{bedroom}\) = 0.32.
b) The probability that a PC is not in a bedroom is 100% minus the probability of it being in a bedroom:
\(P_{ notbedroom}\) = 1 - \(P_{bedroom}\)
\(P_{ notbedroom}\) = 1 - 0.32
\(P_{ notbedroom}\) = 0.68.
c) The expected room to find a PC from a randomly selected household is the room with highest likelihood of having a PC according to Consumer Digest. The Office or den, is the most probable room with a 0.40 chance. You would expect to find a PC in the Office or den.
Full question:
According to Consumer Digest (July/August 1996), the probable location of personal computers (PC) in the home is as follows: Adult bedroom: 0.03 Child bedroom: 0.15 Other bedroom: 0.14 Office or den: 0.40 Other rooms: 0.28 (a) What is the probability that a PC is in a bedroom? (b) What is the probability that it is not in a bedroom? (c) Suppose a household is selected at random from households with a PC; in what room would you expect to find a PC?
To know more about Probability:
brainly.com/question/13604758
#SPJ4
The rule Ry-axis ∘ T⟨5, –3⟩ is used for point (5, –1). Where is the translated point in the coordinate system? A. Quadrant I B. Quadrant II C. Quadrant III D. Quadrant IV
Answers
Answer:
C
Step-by-step explanation:
solve the following 1-step equation for x

Answers
Answer:
x= -12
Step-by-step explanation:
-22+10 = -12
you have to do the opposite operation
The function f(x) = ( )* is translated up 4 units. Which equation represents the translated function?
g() = (5)***
g(x) = ()
g() = ()' +4
g(x) = (13) -4
Answers
Answer:
c
Step-by-step explanation:
Consider the inverse demand function and the inverse supply function P=1+Q Find (a) equilibrium price and, (b) consumers surplus (CS), producers surplus (PS) and the total surplus (TS). Price celling: (i) Find the quantity demanded and quantity supplied when government imposes a price ceiling of $14 per unit. (ii) Find the quantity demanded and quantity supplied when government imposes a price ceiling of $10 per unit. Price floor: (1) Find the quantity demanded and quantity supplied when government imposes a price floor of $12 per unit. (2) Find the quantity demanded and quantity supplied when government imposes a price floor of $8 per unit.thats all the inf we got
p-20q
Answers
To find the equilibrium price and quantities, we need to set the demand and supply functions equal to each other. P and Q = 10 in this case.
Demand: P = 20 - Q
Supply: P = Q
Equating the two equations:
20 - Q = Q
Solving for Q:
2Q = 20
Q = 10
(a) Equilibrium price:
Substituting the equilibrium quantity (Q = 10) into either the demand or supply equation:
P = 10
Therefore, the equilibrium price is $10.
(b) Consumer surplus (CS):
To find consumer surplus, we need to calculate the area below the demand curve and above the equilibrium price.
Consumer surplus = 0.5 * (20 - 10) * 10 = $50
Producer surplus (PS):
To find producer surplus, we need to calculate the area below the equilibrium price and above the supply curve.
Producer surplus = 0.5 * 10 * 10 = $50
Total surplus (TS):
Total surplus is the sum of consumer surplus and producer surplus.
Total surplus = CS + PS = $50 + $50 = $100
Price ceiling:
(i) When a price ceiling of $14 is imposed, the quantity demanded and supplied will be the equilibrium quantity (Q = 10), as the price ceiling does not affect the equilibrium.
(ii) When a price ceiling of $10 is imposed, the quantity demanded will be 10, but the quantity supplied will be determined by the price ceiling of $10.
Price floor:
(1) When a price floor of $12 is imposed, the quantity demanded will be determined by the equilibrium quantity (Q = 10), but the quantity supplied will be 10, as the price floor does not allow prices to go below $12.
(2) When a price floor of $8 is imposed, the quantity demanded and supplied will be the equilibrium quantity (Q = 10), as the price floor does not affect the equilibrium.
Note: Since the inverse supply function is not provided, we assume that it is a linear function with a positive slope, which intersects the inverse demand function at the equilibrium price and quantity.
Learn more about equilibrium price
https://brainly.com/question/29099220
#SPJ11
Which triangles are congruent by ASA?
ABC and TUV
VTU and ABC
VTU and HGF
none of the above

Answers
angle abc and dcb make a linear pair. of abc=2x+9 and dbc=10x+15,find x
Answers
Answer:
x = 13
Step-by-step explanation:
A linear pair of angles sum to 180° , then
2x + 9 + 10x + 15 = 180 , that is
12x + 24 = 180 ( subtract 24 from both sides )
12x = 156 ( divide both sides by 12 )
x = 13
State the feature of a parabola can be obtained from each form of the equation:

Answers
SOLUTION
The standard from of a parabola can be used to obtain the y-intercept
The Factored form can be used to obtain the roots, also known as the x-intercepts.
The Vertex form can be used to obtain the vertex.
Use the distributive property to write an equivalent expression.
4(9k+9m−5)
Answers
Answer:
46k + 36cm - 20
Step-by-step explanation:
Expand 4(9k + 9m - 5) by the distributive property.
Answer:
36k + 36m - 20
Step-by-step explanation:
\(4(9k + 9m - 5) \\\\4 \cdot9k + 4\cdot9m - 4\cdot5 \\\\36k + 36m - 20\)
25.2 dived 6 what the answer
Answers
Answer:
4.2 you should use a calculator for these
Step-by-step explanation:
What is the value of: (3.3) + (-1) - (-1.7)
Answers
Answer:
4
Step-by-step explanation:
3.3 + -1 is 2.3
2.3 - -1.7 is 4
Can someone help me how to do these two please

Answers
Answer:
1.B
2.B
hope this helps
Answer:
B. 62mph
B. 55weeks
Step-by-step explanation:
496 ÷ 8 = 62
15weeks/3houses = x weeks/11houses
15 × 11 ÷ 3 =55weeks
good luck, i hope this helps :)
Construct both a 98% and a 80% confidence interval for B₁. B₁=46, s=5.7, SSzz = 57, n = 12 98%:
Answers
To construct a 98% confidence interval for B₁, we can use the t-distribution since the sample size is small (n = 12).
Given the sample mean (B₁ = 46), sample standard deviation (s = 5.7), and sum of squares (SSzz = 57), we can calculate the confidence interval.
The formula for a confidence interval is:
Confidence Interval = Sample Mean ± (Critical Value * Standard Error)
For a 98% confidence level and n = 12, the critical value is approximately 2.681 (obtained from a t-distribution table).
The standard error is calculated as the sample standard deviation divided by the square root of the sample size (s / √n).
Plugging in the values:
Standard Error = 5.7 / √12 ≈ 1.647
Confidence Interval = 46 ± (2.681 * 1.647)
Therefore, the 98% confidence interval for B₁ is approximately (42.21, 49.79).
In conclusion, we can be 98% confident that the true value of B₁ falls within the range of 42.21 to 49.79 based on the given sample data.
To know more about confidence interval visit :
https://brainly.com/question/15712887
#SPJ11
a doctor is measuring body temperature for patients visiting the office. the doctor believes the average body temperature is less than 98.6 degrees fahrenheit and would like to test this claim. during the process of hypothesis testing, the doctor computes a value from the sample data, which will be used to compare the sample data to the population parameter. what value did the doctor compute? select the correct answer below: critical value test statistic p-value significance level
Answers
Answer: its B) test statistic
Step-by-step explanation:
If you know that the hypotenuse of a 30-60-90 triangle is 124 cm, explain how you find the lengths of the other two sides.
Answers
Answer:
Length of short side is 62 cm and length of long side is \(62\sqrt{3}\) cm
Step-by-step explanation:
There's specific "rule" for 30-60-90 triangle
short leg will be x
long leg will be \(x\sqrt{3}\)
hypotenuse will be 2x
So, when you know hypotenuse is 124 (2x)
To find short leg, you divide 124 by 2
short leg will be 62 (x)
To find long leg, you plug in the x (in this case it's 62)
long leg will be \(62\sqrt{3}\)
which shape has no lines of symmetry, four unequal sides, two right angles and one pair of parallel lines?
Answers
Answer:
circle and two lines that don't touch and are the same length are parrarell
a joker cap is in the form of a right circular cone of base radius 10.5cm and height 36cm. find the area of sheet to make 20 such caps....?
plz answer this
Answers
We know that
l² = r² + h²
l² = (10.5)² + (36)²
l² = 110.25 + 1296
l² = 1406.5
l = √(1406.5)
l = 37.5 cm
Now,
CSA of cone = πrl
=> 22/7 × 10.5 × 37.5
=> 22 × 1.5 × 37.5
=> 1237.5 cm²
Area of 20 caps = 20 × 1237.5
=> 24750 cm²
Answer:
24740 cm²
Step-by-step explanation:
First let us find the slant height (l) of the corn
l² = r² + h²
l² = (10.5)² + (36)²
l² = 110.25 + 1296
l² = 1406.25
l = √1406.25
l = 37.5 cm
Now let us use this formula to find the area of a corn
π r l
π × 10.5 × 37.5
1237.00 cm²
And now let's find the area of 20 caps or corns
1237.00 × 20
24740 cm²
Hope this helps you :-)
1. Consider a stock and assume it follows a geometric Brownian motion dS = µdt+σdz. Consider now a function G = G(S, t).
i) Use Itˆo’s lemma to find the stochastic process dG followed by G^2.
ii) Show that this value satisfies the Black-Scholes-Merton Partial Differential Equation :
Answers
The stochastic process for the function G = G(S, t) is given by:
\(\[dG = \frac{\partial G}{\partial t}dt + \frac{\partial G}{\partial S}dS + \frac{1}{2}\frac{\partial^2 G}{\partial S^2}(dS)^2\]\)
The stochastic process for G^2 is given by:
\(\[d(G^2) = \left[2G\frac{\partial G}{\partial t} + \left(\frac{\partial G}{\partial t}\right)^2 + 2G\frac{\partial G}{\partial S} + \left(\frac{\partial G}{\partial S}\right)^2\right]dt + 2G\frac{\partial^2 G}{\partial S^2}(dS) + \left(\frac{\partial G}{\partial t}\right)^2(dt)^2 + \left(\frac{\partial G}{\partial S}\right)^2(dS)^2\]\)
Let us now analyze each section in a detailed way:
i) Using Ito's lemma, we can find the stochastic process \($dG$\) followed by \($G^2$\) as follows:
Applying Ito's lemma to \($G(S, t)$\), we have:
\(\[dG = \frac{\partial G}{\partial t}dt + \frac{\partial G}{\partial S}dS + \frac{1}{2}\frac{\partial^2 G}{\partial S^2}(dS)^2.\]\)
For \($G = G(S, t)$\), the first term \($\frac{\partial G}{\partial t}dt$\) is straightforward as it is the partial derivative of \($G$\) with respect to \($t$\) multiplied by \($dt$\).
The second term \($\frac{\partial G}{\partial S}dS\) can be obtained by taking the partial derivative of $G$ with respect to \($S$\) and multiplying it by \($dS\).
The third term \($\frac{1}{2}\frac{\partial^2 G}{\partial S^2}(dS)^2\) involves the second partial derivative of \($G$\) with respect to \($S$\), and it is multiplied by \($(dS)^2\).
ii) To find the stochastic process for $G^2$, we substitute $G = G(S, t)$ into the equation derived above:
\(\[d(G^2) = 2GdG + (dG)^2.\]\)
Expanding and substituting the value of $dG$, we get:
\(\[d(G^2) = 2G\left(\frac{\partial G}{\partial t}dt + \frac{\partial G}{\partial S}dS + \frac{1}{2}\frac{\partial^2 G}{\partial S^2}(dS)^2\right) + \left(\frac{\partial G}{\partial t}dt + \frac{\partial G}{\partial S}dS + \frac{1}{2}\frac{\partial^2 G}{\partial S^2}(dS)^2\right)^2.\]\)
Simplifying the above expression, we can write:
\(d(G^2) &= \left[2G\frac{\partial G}{\partial t} + \left(\frac{\partial G}{\partial t}\right)^2 + 2G\frac{\partial G}{\partial S} + \left(\frac{\partial G}{\partial S}\right)^2\right]dt &\quad+ 2G\frac{\partial^2 G}{\partial S^2}(dS) + \left(\frac{\partial G}{\partial t}\right)^2(dt)^2 + \left(\frac{\partial G}{\partial S}\right)^2(dS)^2.\)
The above equation represents the stochastic process for $G^2$.
To know more about Ito's lemma , refer here:
https://brainly.com/question/30759610#
#SPJ11
i am having a very hard time remembering Negative and Positive numbers adding, subtracting, multiplying, and dividing them.
Here are some examples :
-4+(-25)
-9-(-3)
4÷ - ( -8 )
(-15) (-7)
Answers
Answer:
Step-by-step explanation:
So negitive have the - besides it and + mean its negative .
Answer:
-29
-6
.5
105
Step-by-step explanation:
I need help on this for a brainly
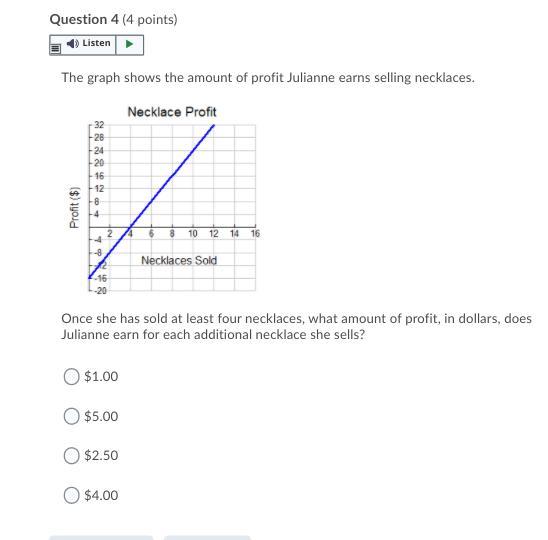
Answers
Answer:
D) $4.00
Step-by-step explanation:
This is because looking closely, the slope is 8/2, it goes up 8 and over 2 make it 8 divided by 2 giving you 4, therefore the choice narrow down to 4, or 4 dollars
You school plans to collect at least 1500 pairs of socks for the homeless shelter. So far they have collected 183 pairs of socks. There are 4 days left of the sock drive. Write an inequality and solve to represent the average number of pairs of socks to be collected each of the last 4 days.
Answers
Answer: the amount of socks they will collect in four days is less than the amount of socks they plant to collect, in other words 915<1500 socks.
Step-by-step explanation:
If they collect 183 pairs of socks in one day, and there are four days left, then 183 x 5 = 915 (pairs of socks) in five days. They need to collect 1,500 pairs.
use a model for security purposes a jewelry company prints a hidden watermark on the logo of its official documents. the watermark is a chord located 0.7 cm from the center of a circular ring that has a 2.5 cm radius. to the nearest tenth, what is the length of the chord?
Answers
The length of the chord located 0.7 cm from the centre of a circular ring with a 2.5 cm radius is approximately 3.5 cm.
To calculate the length of the chord, we can use the following formula:
Chord Length = 2 x √(r^2 - d^2)
Where r is the radius of the circular ring and d is the distance between the chord and the centre of the circle.
In this case, r = 2.5 cm and d = 0.7 cm. Plugging these values into the formula, we get:
Chord Length = 2 x √(2.5^2 - 0.7^2) ≈ 3.5 cm (rounded to the nearest tenth)
Therefore, the length of the chord is approximately 3.5 cm. This hidden watermark technique is a simple but effective security measure that can help prevent counterfeiting or tampering with important documents. By incorporating a unique and difficult-to-replicate watermark, the jewellery company can protect its brand identity and ensure the authenticity of its official documents.
Learn more about chord, here:
brainly.com/question/20969446
#SPJ11
"7
A polynomial \( P \) is given. Find all zeros of \( P \), real and Complex. Factor \( P \) completely. \[ \begin{array}{ll} 1 & P(x)=x^{4}+4 x^{2} \\ 3 & P(x)=x^{3}-2 x^{2}+2 x \\
Answers
1) For the polynomial \(P(x) = x^4 + 4x^2\):
The zeros of \(P\) are \(x = 0\) (with multiplicity 2) and \(x = \pm 2i\) (complex zeros). The polynomial can be factored as \(P(x) = x^2(x^2 + 4)\).
To find the zeros of \(P(x)\), we set \(P(x)\) equal to zero and solve for \(x\):
\[x^4 + 4x^2 = 0.\]
We can factor out a common term of \(x^2\) from both terms:
\[x^2(x^2 + 4) = 0.\]
Using the zero product property, we set each factor equal to zero:
\[x^2 = 0 \quad \text{and} \quad x^2 + 4 = 0.\]
For the first equation, \(x^2 = 0\), we find \(x = 0\) with multiplicity 2. For the second equation, \(x^2 + 4 = 0\), we subtract 4 from both sides and take the square root:
\[x^2 = -4 \quad \Rightarrow \quad x = \pm 2i.\]
Therefore, the zeros of \(P(x) = x^4 + 4x^2\) are \(x = 0\) (with multiplicity 2) and \(x = \pm 2i\). The polynomial can be factored as \(P(x) = x^2(x^2 + 4)\).
2) For the polynomial \(P(x) = x^3 - 2x^2 + 2x\):
The zeros of \(P\) are \(x = 0\) (with multiplicity 1) and \(x = \pm 1\) (real zeros). The polynomial can be factored as \(P(x) = x(x-1)(x+1)\).
To find the zeros of \(P(x)\), we set \(P(x)\) equal to zero and solve for \(x\):
\[x^3 - 2x^2 + 2x = 0.\]
We can factor out a common term of \(x\) from each term:
\[x(x^2 - 2x + 2) = 0.\]
Using the zero product property, we set each factor equal to zero:
\[x = 0, \quad x^2 - 2x + 2 = 0.\]
The quadratic equation \(x^2 - 2x + 2 = 0\) does not have real solutions, as its discriminant (\(-2^2 - 4(1)(2) = -4\)) is negative. Therefore, there are no additional real zeros.
Therefore, the zeros of \(P(x) = x^3 - 2x^2 + 2x\) are \(x = 0\) (with multiplicity 1) and \(x = \pm 1\). The polynomial can be factored as \(P(x) = x(x-1)(x+1)\).
To know more about polynomial, visit
https://brainly.com/question/1496352
#SPJ11
What is the equation of the line that is perpendicular to y = -2/3x+4 and that passes through (-2,-2)
Answers
Answer:
y = 3/2x + 1
Step-by-step explanation:
y = 3/2x + b
-2 = 3/2(-2) + b
-2 = -3 + b
1 = b
50- - 60 -16
What is the answer
Answers
94 cause 50- -60=110 then 110-16=94
Annie works at a library. She worked for a total of 11 hours in the last 5 days and worked an equal amount of time each day. What is the correct way to show how to find the number of hours she worked each day?
Answers
each day is 24 hours.
so minus 11 from 24 , 5 times, since theyre 7 days in a week.
I THINK IVE ALREADY LEARNED THIS BUT IM NOT GREAT AT MATH <3
x+8=6 you have to solve for x.
Answers
Answer:
x= -2
Step-by-step explanation:
8-2=6
also, 8-8=0, 6-8= -2
x=-2
Hope this helps:)- please crown me brainliest!
find the value of "y" in the triangle.

Answers
Answer:
y = 7 x = 45
Step-by-step explanation:
\(x=45\) because the triangle is a right angle isocele triangle so 180-90 =90
90 / 2 =45 = x
\(\frac{7\sqrt{\:2}}{\sin \left(90\right)\:}=\frac{y}{\sin \left(45\right)}\) so y = 7
Answer:
y =7
this is your answer
Carson can choose one vehicle (car or truck), one color (blue, red, or silver), and one type of transmission (standard or automatic). How many possible outcomes are there?
Answers
Answer:
12 possible outcomes
Step-by-step explanation:
Choosing 1 vehicle from 2 = 2C1 = 2
Choosing 1 color from 3 = 3C1 = 3
Choosing 1 type from 2 = 2C1 = 2
Number of possible outcomes :
2C1 * 3C1 * 2C1
2 * 3 * 2
= 12 different possible outcomes