2. Create a sequence to fit the given criteria. Describe your
sequence using figures, words, or numbers. Provide the first
four terms of the sequence. Explain how you know that it is
a sequence.
a. Create a sequence that begins with a positive integer, is
decreasing by multiplication, and is finite.
Need help quick please
Answers
A geometric sequence with first term 16 and common ratio 0.5, with 10 terms, satisfies the requirements for this problem, and the first four terms are:
16, 8, 4, 2.
What is a geometric sequence?A geometric sequence is a sequence in which the result of the division of consecutive terms is always the same, called common ratio q.
The nth term of a geometric sequence is given by:
\(a_n = a_1q^{n-1}\)
In which \(a_1\) is the first term.
For this problem, we have that:
Sequence begins with a positive integer, hence the first term is 16. (chosen value, any positive integer suffices).The sequence is decreasing by multiplication, hence q > 0 and q < 1, q = 0.5 is a possible value and the sequence is geometric.A finite number of terms, we chose 10.Each term is the previous term multiplied by 0.5, hence the first four terms are:
16, 8, 4, 2.
More can be learned about geometric sequences at https://brainly.com/question/24643676
#SPJ1
Related Questions
Make a rap about why a parallelogram is the best shape. Must be appropriate and at least a minute long. Giving brainless to whoever answers!!!
Answers
Ahem, here goes, my attempt at a minute-long rap in praise of the parallelogram:
Yo, listen up, the parallelogram is where it's at,
A shape so brilliant, the angles are sat.
Parallel sides that never converge,
Internal angles that never diverge.
Each side an equal length,
A geometry prodigy's dream length.
The diagonals intersect, another line through the middle they meet,
Creating symmetry so neat.
A rectangle it could be,
But it's oblong, not square, can't you see?
With depth and width in perfect balance we see,
A two-dimensional form of complexity.
While the square is simple, the parallelogram is hip,
A mathematical masterpiece, skip, skip, skip!
four right angles keep the shape so tight,
Parallel lines dominate left and right.
Rotated or reflected without a care,
Its structural integrity beyond compare.
triangles form at each corner you'll note,
Acute or obtuse, depends on the protractor's groove.
A versatile shape with reason and purpose galore,
The parallelogram, simply, carries the floor.
From geometry to art, its angles they intrigue,
As a basis for patterns, its potential we can truly plug.
A forgotten form that deserves more acclaim,
Put the parallelogram on geometry's game!
This shape so underrated, rarely appreciated it seems,
But with logic and virtue, strong foundations it gleams.
The parallelogram, the parallelogram, Hooray!
This is why the parallelogram is the best shape, I say!
find the range of the function y = 1/2x + 2 if the domain is {-4, -2, 0}
Answers
The range of the function y = 1/2 x + 2 is {0, 1, 2}, if the domain of the function is {-4, -2, 0}.
What is function?An expression, rule, or law in mathematics that specifies the relationship between an independent variable and a dependent variable.
The given function is,
y = 1/2 x + 2.
Also, the domain of the function is {-4, -2, 0}.
Since, the domain of the functions defines the values of x,
And range defines the value of y in function.
The value of y at x = -4
y = 1/2(-4) + 2 = -2 + 2 = 0
At x = -2,
y = 1/2(-2) + 2 = -1 + 2 = 1
At x= 0,
y = 1/2 (0) + 2 = 2
The values of y are 0, 1 and 2.
Hence, the range of the function is {0, 1, 2}.
To know more about Function on:
https://brainly.com/question/2411204
#SPJ1
State the name of the property illustrated.
4(-8+5)= - 32 + 20
Answers
The property illustrated in equation 4(-8+5) = -32 + 20 is the Distributive Property.
The Distributive Property states that when a number is multiplied by a sum or difference in parentheses, it can be distributed or multiplied by each term inside the parentheses separately, and then the results can be added or subtracted.
In this case, the number 4 is multiplied by the sum (-8 + 5). By applying the Distributive Property, we distribute the 4 to each term inside the parentheses:
4(-8 + 5) = (4 * -8) + (4 * 5)
This simplifies to:
4(-8 + 5) = -32 + 20
Finally, we can perform the addition:
-32 + 20 = -12
Therefore, the equation demonstrates the application of the Distributive Property.
know more about Distributive Property here:
https://brainly.com/question/2807928
#SPJ8
Please help me with both questions.

Answers
Answer:
3.) m < 7 = 155°, m < 8 = 25°
4.) m < 5 = 30°
m < 6 = 30°
m < 7 = 60°
m < 8 = 60°
Step-by-step explanation:
3.) By definition, angles that do not share a common side are called nonadjacent angles. Two nonadjacent angles formed by two intersecting lines are called vertical angles.
Given that < PQT + < TQR = 180°Then it also means that the sum of m < 7 and m < 8 will also equal 180°. Also, < PQT ≅ < SQR because they are vertical angles, therefore, their measurements must also be congruent. Similarly, < PQS ≅ < TQR because they are vertical angles, and their measurements must also be congruent.m < 7 = 5x + 5
m < 8 = x - 5
m < 7 + m < 8 = 180°
Substitute the values of m < 7 and m < 8 into the equation:
5x + 5 + x - 5 = 180°
6x + 0 = 180°
6x = 180°
Divide 6 on both sides of the equation to solve for x:
\(\frac{6x}{6} = \frac{180}{6}\)
x = 30°
Plug in x = 30° to find the value of m< 7 and m< 8:
m < 7 = 5x + 5 = 5(30) + 5 = 150 + 5 = 155°
m < 8 = x - 5 = 30 - 5 = 25°
4.) This problem is an example of angles on a straight line. By definition, the sum of angles on a straight line is equal to 180°.
Therefore, the measurements of the following angles add up to 180°:
< UVX + < XVY + < YVZ + <ZVW = 180° m < 5 + m < 6 + m < 7 + m < 8 = 180°m < 5 = 5x
m < 6 = 4x + 6
m < 7 = 10x
m < 8 = 12x - 12
Substitute the values of each measurement onto the following equation:
5x + 4x + 6 + 10x + 12x - 12 = 180°
Combine like terms:
31x - 6 = 180°
Add 6 on both sides of the equation:
31x - 6 + 6 = 180° + 6
31x = 186
Solve for x:
\(\frac{31x}{31} = \frac{186}{31}\)
x = 6
Plug in x = 6° to find the values of m < 5, m < 6, m < 7, and m < 8:
5(6) + 4(6) + 6 + 10(6) + 12(6) - 12 = 180°
180° = 180°
Therefore:
m < 5 = 5(6) = 30°
m < 6 = 4(6) + 6 = 30°
m < 7 = 10(6) = 60°
m < 8 = 12(6) - 12 = 60°
During science class, groups measure out different volumes of vinegar. The line plot below shows the amount of vinegar used by 12 1212 groups, rounded to the nearest 1 2 mL 2 1 mLstart fraction, 1, divided by, 2, end fraction, start text, space, m, L, end text. 4 4 4 1 2 4 2 1 5 5 5 1 2 5 2 1 6 6 6 1 2 6 2 1 7 7 7 1 2 7 2 1 8 8 A line plot labeled 4 to 8 with tick marks every one-half unit labeled with a tick mark and number. Above tick mark four and one-half there is a column of two dots. Above tick mark 5 there is a column of three dots. Above tick mark six and one-half there is a column of two dots. Above tick mark 7, there is a column of two dots. Above tick mark seven and one-half, there is a column of three dots. What is the total amount of vinegar, in milliliters, used by the 3 33 groups that used the most? mL mL
Answers
Answer:
22 1/2
Step-by-step explanation:
Solve for d. d−(−12)=100
Answers
Answer:
A - 6
Step-by-step explanation:
The lines are parallel.
Theorem: If two parallel lines are cut by a transversal, then same side interior angles are supplementary.
The angles measuring 16x + 4 and 80 are supplementary, so thjeir measures add to 180.
16x + 4 + 80 = 180
16x + 84 = 180
16x = 96
x = 6
Deandre's chocolate bar is 53% cocoa. If the weight of the chocolate bar is 69 grams, how many grams of cocoa does it contain? Round your answer to the nearest tenth.
Answers
The grams of cocoa does it contains is 36.57 grams
How many grams of cocoa does it contains?From the question, we have the following parameters that can be used in our computation:
Weight of the chocolate bar = 69
Proportion = 53%
This implies that
Grams of cocoa = weight of the chocolate bar * Proportion
Substitute the known values in the above equation, so, we have the following representation
Grams of cocoa = 53% * 69
Evaluate the products
Grams of cocoa = 36.57
Read more about percentage at
https://brainly.com/question/843074
#SPJ1
Assume that Lines L and M are parallel. Find a pair of acute, corresponding angles.
Select all that apply.
A. q and w
B. r and y
C. x and s
D. q and y
E. s and y
F. r and x
G. t and w
H. t and z

Answers
Answer:
Choice E and F
Step-by-step explanation:
acute = less than 90
please help me solve

Answers
The equation for the line of best fit is: C. y = 0.894x + 0.535.
How to determine the equation for the line of best fit?In order to determine the equation for the line of best fit, we would create a table of values based on the given x-values and y-values as follows;
x y x² y² xy__
5 4 25 16 20
6 6 36 36 36
9 9 81 81 81
10 11 100 121 110
14 12 196 144 168
Sum 438 398 415
Next, we would calculate the mean of the x and y variables as follows;
Mean = [∑(x)]/n
Mean = 44/5
Mean, \(\bar{x}\) = 8.8
Mean = [∑(y)]/n
Mean = 42/5
Mean, \(\bar{y}\) = 8.4
∑(x - \(\bar{x}\))(x - \(\bar{y}\)) = (5-8.8)(4-8.4) + (6-8.8)(6-8.4)+(9-8.8)(9-8.4)+(10-8.8)(11-8.4)+(14-8.8)(12-8.4)
∑(x - \(\bar{x}\))(x - \(\bar{y}\)) =45.4
∑(x - \(\bar{x}\))² = (5-8.8)²+(6-8.8)²+(9-8.8)²+(10-8.8)²+(14-8.8)²
∑(x - \(\bar{x}\))² = 50.8
Now, we can determine the slope coefficient for the line of best fit:
Slope (b) = 45.4/50.8
Slope (b) = 0.894.
Lastly, we would determine the intercept (a) as follows;
\(a = \bar{y} - b\bar{x}\)
a = 8.4 - (0.894)8.8
a = 0.535
Therefore, the required equation is y = 0.894x + 0.535.
Read more on linear regression here: brainly.com/question/16793283
#SPJ1
Use the diagram to find the angle measures
of the triangle. Recall that the sum of the
angle measures of a triangle is 180º.
9x
(x+4)
.
x =
(x+4)° = °
9x =

Answers
Answer:
x=16
(x+4)=20
9x=144
Step-by-step explanation:
9x+x+4+x=180
11x+4=180
11x=180-4
11x=176
\(x = \frac{176}{11} \)
x=16
which terms are like terms in the expression 5x + 9 + (-7x)
Answers
Answer:
5x and -7x
Step-by-step explanation:
they both end in the variable "x"
At a local college, only 30% of students live off campus. Of those who live off campus, 62% of those students get a part-time job. Of those who live on campus, 65% work part-time. The tree diagram shows how the college students are divided into subgroups.
The tree diagram shows college students branching off into two categories, off campus and on campus students. Off campus students branches off into two sub-categories, work part-time and do not work. On campus branches off into two subcategories, work part-time and do not work.
What is the percentage of students who live on campus who do not have a part-time job?
18.6%
24.5%
35%
38%
Answers
Answer:
24.5%
Step-by-step explanation:
Given
P(Off-Campus) = 0.30
P(Part-Time Job | Off-Campus) = 0.62
P(Part-Time Job | On-Campus) = 0.65
Inferred
P(On-Campus) = 0.70
P(No Part-Time Job | Off-Campus) = 0.38
P(No Part-Time Job | On-Campus) = 0.35
Calculation
P(No Part-Time Job | On-Campus) = P(No Part-Time Job ∩ On-Campus)/P(On-Campus)
0.35 = P(No Part-Time Job ∩ On-Campus)/0.70
0.245 = P(No Part-Time Job ∩ On-Campus)
Therefore, 24.5% of students that live on campus do not have a part-time job.
how can i solve it? Which point would be a solution to the system of linear inequalities shown below y < -x + 4 y > - 3x - 8A- (-10,10) B- (-2,-7)C- (11,-10) D- (-6,3)
Answers
The answer is C) (11,-10)
A triangle has a base length of 3ac2 and a height 2 centimeters more than the base length. Find the area of the triangle if a = 2 and c = 3.
Answers
The area of the triangle, when a = 2 and c = 3, is 1512 square centimeters.
We must apply the formula for the area of a triangle, which is provided by: to determine the triangle's area.
(1/2) * Base * Height = Area
We can enter the values of a = 2 and c = 3 into the formula given that the base length is 3ac2 and the height is 2 centimetres greater than the base length.
Base length =\(3ac^2 = 3 * 2 * (3^2) = 3 * 2 * 9 = 54\) centimeters
Height is calculated as Base Length + 2 (54 + 2 = 56 centimetres).
Using these values as a substitute in the formula, we obtain:
Area =\((1/2) * 54 * 56 = 1512\) square centimeters
centimetres square
It's crucial to understand that the calculation assumes the triangle is a right triangle with the specified base and height and that the given values of a and c are accurately used in the formula.
for more such questions on triangle
https://brainly.com/question/25215131
#SPJ8
Given that 8 tan = 3 cos
a) Show that the above equation can be rewritten in the form 3 sin2 + 8 sin − 3 = 0
b) Hence solve, for 0 ≤ ≤ 90, the equation 8 tan 2 = 3 cos 2, giving your answers to 2 decimal places.
Answers
The only solution for the equation 8 tan^2 θ = 3 cos^2 θ in the given Range is θ ≈ 19.47 degrees.
a) We are given the equation 8 tan θ = 3 cos θ.
Dividing both sides of the equation by cos θ, we have:
8 tan θ / cos θ = 3
Using the identity tan θ = sin θ / cos θ, we can substitute it into the equation:
8 (sin θ / cos θ) / cos θ = 3
Simplifying further, we get:
8 sin θ / cos^2 θ = 3
Now, multiplying both sides of the equation by cos^2 θ, we have:
8 sin θ = 3 cos^2 θ
Using the identity cos^2 θ = 1 - sin^2 θ, we can substitute it into the equation:
8 sin θ = 3(1 - sin^2 θ)
Expanding the equation, we get:
8 sin θ = 3 - 3 sin^2 θ
Rearranging the terms, we have:
3 sin^2 θ + 8 sin θ - 3 = 0
Therefore, we have successfully shown that the equation can be rewritten in the form 3 sin^2 θ + 8 sin θ - 3 = 0.
b) Now, let's solve the equation 3 sin^2 θ + 8 sin θ - 3 = 0.
To solve the quadratic equation, we can use factoring, quadratic formula, or other appropriate methods.
In this case, the equation factors as:
(3 sin θ - 1)(sin θ + 3) = 0
Setting each factor equal to zero, we have two equations:
3 sin θ - 1 = 0 or sin θ + 3 = 0
For the first equation, solving for sin θ, we get:
3 sin θ = 1
sin θ = 1/3
Taking the inverse sine (sin^-1) of both sides, we find:
θ = sin^-1(1/3) ≈ 19.47 degrees (to 2 decimal places)
For the second equation, solving for sin θ, we have:
sin θ = -3
Since the range of sine is between -1 and 1, there are no solutions for this equation in the given range (0 ≤ θ ≤ 90 degrees).
Therefore, the only solution for the equation 8 tan^2 θ = 3 cos^2 θ in the given range is θ ≈ 19.47 degrees.
To know more about Range .
https://brainly.com/question/30389189
#SPJ11
The length of a rectangle is six times the width. The perimeter of the rectangle is 28 inches. What is the area of the rectangle (in square inches)?
Answers
Answer:
24sq.in
Step-by-step explanation:
Let, length be x and width be y.
x= 6y
2(x+y)=28
or, 2(6y+y)=28
or, 2×7y=28
or, 14y =28
y=2
x= 6×2=12
area= 12×2 = 24 sq.in
(-1)³
how what is the answer please help
Answers
A spinner is divided into three sections: red, blue, and green. The red section is 2/5 of the area of the spinner. The blue section is 1/2 of the area of the spinner. Give the probability for each outcome. Express your answers as fractions.
Answers
Probability of red = \(\frac{4}{10}\) , blue = \(\frac{5}{10}\) , green = \(\frac{1}{10}\).
Meaning of probability :
Probability is calculation of how likely some event will happen. Whenever we are not sure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are going to happen.
The analysis of events governed by probability is called statistics.
According to the given information :
Red section = \(\frac{2}{5}\)
multiply numerator and denominator by \(2\) we get
Red section = \(\frac{4}{10}\)
Blue section = \(\frac{1}{2}\)
multiply numerator and denominator by \(5\) we get
Blue section = \(\frac{5}{10}\)
Green section = \(1\)- Red section - Blue section
Green section =\(1-\frac{4}{10} -\frac{5}{10}\)
Green section = \(\frac{1}{10}\)
Therefore Probability of red = \(\frac{4}{10}\) , blue = \(\frac{5}{10}\) , green = \(\frac{1}{10}\).
Learn more about Probability
https://brainly.com/question/11234923
#SPJ1
Question 6
1 pts
Translate the following statement into an equation: Sequals the quotient of rand the difference of r
and 4.
OS=s - (r – 4)
OS=144
OS=r(r - 4)
S= A
Question 7
1 pts
Answers
Answer:
add, subtract, multiply and divide complex numbers much as we would expect. We add and subtract
complex numbers by adding their real and imaginary parts:-
(a + bi)+(c + di)=(a + c)+(b + d)i,
(a + bi) − (c + di)=(a − c)+(b − d)i.
We can multiply complex numbers by expanding the brackets in the usual fashion and using i
2 = −1,
(a + bi) (c + di) = ac + bci + adi + bdi2 = (ac − bd)+(ad + bc)i,
and to divide complex numbers we note firstly that (c + di) (c − di) = c2 + d2 is real. So
a + bi
c + di = a + bi
c + di ×
c − di
c − di =
µac + bd
c2 + d2
¶
+
µbc − ad
c2 + d2
¶
i.
The number c−di which we just used, as relating to c+di, has a spec
Keegan is determining whether the triangle with vertices L(-1, 3), M(5, 5) and N(7, -1) is a right triangle. Keegan finds the slopes as shown and concludes that the triangle is not a right triangle because the product is not -1. What is his error and what should he do to correct it?
(added an image)
will mark brainiliest

Answers
Keegan's error is assuming that the product of the slopes of any two sides of a triangle should be -1 for the triangle to be a right triangle.
To determine if the triangle LMN is a right triangle, Keegan should instead calculate the lengths of the three sides of the triangle and check if they satisfy the Pythagorean theorem.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
To correct his approach, Keegan should calculate the lengths of sides LM, MN, and NL using the coordinates of the vertices and then check if the Pythagorean theorem holds true.
If the squared length of one side is equal to the sum of the squares of the other two sides, then the triangle LMN is a right triangle.
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ1
There are 15 pieces of the same size candy in a bag. Four are banana flavored, three strawberry flavored, and two orange flavored. What would be the probability of picking an orange or a cherry flavored candy from the bag? Write your answer as percent rounded to the nearest tenth.

Answers
Given:
Total number of candy in a bag is 15.
Number of orange flavored candy is 2
Number of cherry flavored candy is 6
Let A be the event of picking an orange or a cherry flavored candy from the bag.
\(\begin{gathered} n(A)=2+6 \\ n(A)=8 \end{gathered}\)\(P(A)=\frac{8}{15}\)\(\begin{gathered} \text{Percentage}=\frac{8}{15}\times100 \\ \text{Percentage}=53.3\text{ \%} \end{gathered}\)The average daily balance of a credit card for the month of November was $700, and the unpaid balance at the end of the month was $1,400. If the annual percentage rate is 15.6% of the average daily balance, what is the total balance on the next billing date December 1? Round your answer to the nearest cent.
Answers
Answer:
Step-by-step explanation:
To calculate the total balance on the next billing date, we need to consider the average daily balance and the unpaid balance from the previous month.
Given:
Average daily balance for November = $700
Unpaid balance at the end of November = $1,400
Annual percentage rate (APR) = 15.6%
Step 1: Calculate the interest charged for the month of November.
Interest = (Average daily balance * APR * Number of days in the month) / 365
Number of days in November = 30
Interest = (700 * 0.156 * 30) / 365 = $36.44 (rounded to the nearest cent)
Step 2: Add the interest to the unpaid balance to get the total balance on December 1.
Total balance = Unpaid balance + Interest
Total balance = $1,400 + $36.44 = $1,436.44
Therefore, the total balance on the next billing date, December 1, is $1,436.44 (rounded to the nearest cent).
The total balance on the next billing date December 1 is $1,509.20.
What is an annual percentage rate?The annual interest produced by a sum that is paid to investors or charged to borrowers is referred to as the annual percentage rate (APR).
Given,
The average daily balance of a credit card for November = is $700Unpaid balance at the end of the month = $1,400The annual percentage rate = 15.6%Then, the percentage rate for November = \(\sf\frac{15.6}{100}\) × 700
\(\sf = \$109.20\)
Balance on 1st December = unpaid balance at the end of November + percentage rate
\(\sf = $1400 +$109.20\)
\(\sf =\$1509.20\)
Therefore, the total balance on the next billing date December 1 is $1,509.20.
To learn more about percentage rate, visit:
https://brainly.com/question/30127793
Simplify the expression.
15+(-3) - 4/5j - 2/5j + 5=
Answers
85j-6/5j
Hope this helped.
Which scenario is modeled in the diagram below? Percents Total 80% 20% 100% 20% 20% 20% 20% $6.87 Dimitri used a coupon that saved him 80 percent, or $6.87. He paid $34.35 for the items. Dimitri used a coupon that saved him 80 percent, or $27.48. He paid $34.35 for the items. Dimitri used a coupon that saved him 80 percent, or $6.87. The price of the items before the discount was $34.35. Dimitri used a coupon that saved him 80 percent, or $27.48. The price of the items before the discount was $34.35.
Answers
Answer: Answer is D
Step-by-step explanation: Took the quiz in EDJENUITY
d fgrthrthrhtrhtrhtrhrhrthrh
Kate Drew has been hand-painting wooden Christmas ornaments for several years. Recently, she has hired some friends to help her increase the volume of her business. In checking the quality of the work, she notices that some slight blemishes occasionally are apparent. A sample of 24 pieces of work resulted in the following number of blemishes on each piece: 1,1,2,3,1,0,2,0,0,1,3,1,0,1,2,0,0,2,1,2,3,2,1,1. Develop upper and lower control limits (99.73%) for the number of blemishes on each piece. Is the process in control? Why? **Please do this in excel*
Answers
A sample of 24 pieces of work is considered for the checking the quality of the work,
a) Upper control limit of 99.73% confidence interval is 4
Lower control limit of 99.73% confidence interval is Zero.
The process is in control because all the values of the blemishes per unit are lie within the control limits .
What is Control Limits?The Control limits consist of two limits lower control limit and upper control limit within which the value of the statistical observations of a product are expected to lie. If the values lie outside these limits, then the process is called out of statistical control. We have,
Kate Drew has been hand-painting wooden Christmas ornaments for several years.
Sample size = 24 pieces
confidence level = 99.73% = 0.9973
The number of blemishes per unit is given as:
1,1,2,3,1,0,2,0,0,1,3,1,0,1,2,0,0,2,1,2,3,2,1,1.
The control limits are to be computed for the number of defects per piece . Let us consider the number of defects per piece be denoted by c. In that case, the control limits for c chart are used. The upper control limit (UCL) and lower control limit (LCL) for c chart is given by,
UCL = c-bar + 3 s.d
LCL = c-bar - 3 s.d
where c-bar = 1/n(€c) average number of defects
So, c-bar is computed as,
c-bar = (1+1+2+3+1+0+2+0+0+1+3+1+0+ 1+2+0 +0+2 + 1+2 +3+ 2+1+1) /24 = 30/24 = 1.25
put the data in Excel sheet and calculate required limits using Excel Commands.
Excel Command for Average, c-bar
=Average( Range of numbers who's average you want to calculate )
In my excel sheet, = Average ( H2 : H25)
= 1.25
Excel Command for Standard deviations,
=STDEV( numbers who's standard deviations you want to calculate)
here, =STD(H2:H25) , output= 0.98907
UCL = 1.25 + 3( 0.98907)
= 4.217
LCL = 1.25 - 3( 0.98907)
= - 1.717
but defective item can never be negative so, Lower control limit is Zero.
Hence, for the given data, the upper control limit for the number of defects is 4 and the lower control limit is 0.
To learn more about Contral limits of confidence interval, refer:
https://brainly.com/question/15712887
#SPJ4

What is the place value of the 8 in 45.1386? a. Tenths
b. Tens
c. Thousands d. Thousandths
2. What is the place value of 1 in 0.5431? a. Thousands
b. Thousandths
c. Tenthousandths d. Ten thousands
3. What is the place value of 9 in 5.9105 a. Tenths
b. Tens
c. Hundredths d. hundreds
4. Whichdigithastheleastvaluein5.1896 a. 1
b. 8 c. 9 d. 6
5. Which decimal place value has the greatest value? a. Tenths
b. Hundredths
c. Thousandths
d. Ten thousandths
6. How to read and write 5.04? a. Fiveandfourtenths
b. Five and four hundredths
c. Fiveandfourthousandths
d. Five and four ten
Answers
Answer:
1. d thousandths
2. c ten thousandths
3. a tenths
4. d 6
5. a tenths
6. b five and four hundredths
Step-by-step explanation:
So far, I got 2 out of 5 for finding the radius but I don't know the rest

Answers
Answer:
∠ABD≈31.974°
Step-by-step explanation:
Since BD is a diameter, ΔABD is a right triangle with BD as its hypotenuse.
Using BD=d, solve for ∠ABD using sin⁻¹(4.5/d)
Complete this sequence of numbers such that the difference between any two adjacent numbers is the same : 3/k, _, _, 9/2k.
Answers
The completed sequence is: 3/k, 3/k, 3/k, 9/2k.To complete the sequence of numbers with a constant difference between adjacent numbers, we can calculate the common difference by subtracting the first term from the second term.
Let's denote the missing terms as A and B.
The given sequence is: 3/k, A, B, 9/2k.
The common difference can be found by subtracting 3/k from A or B. Therefore:
A - 3/k = B - A = 9/2k - B.
To simplify, we can equate the two expressions for the common difference:
A - 3/k = 9/2k - B.
Next, we can solve for A and B using this equation.
Adding 3/k to both sides gives:
A = 3/k + 9/2k - B.
Now, we can substitute the value of A into the equation:
3/k + 9/2k - B - 3/k = 9/2k - B.
Simplifying further, we have:
9/2k - 3/k = 9/2k - B.
Cancelling out the common terms, we find:
-3/k = -B.
Multiplying both sides by -1, we get:
3/k = B.
For more such questions on Adjacent numbers:
https://brainly.com/question/28207765
#SPJ8
suppose 77% of students chose to study French their junior year, and that meant that there were 616 such students. How many chose not to take French their junior year?
Answers
Notice that if we find the total number of students, we can find the number of those that decided not to take French by subtracting the ones that took French from the total number of students.
We have the next relations:
\(\begin{gathered} 616\to77\text{percent} \\ x\to100\text{percent} \end{gathered}\)In other words:
\(\begin{gathered} \frac{616}{77}=\frac{x}{100} \\ \Rightarrow x=\frac{616\cdot100}{77} \\ \Rightarrow x=800 \end{gathered}\)Then, there are 800 students in total
The number of students that did not choose to take French their junior year is:
\(800-616=184\)184 is the answer.
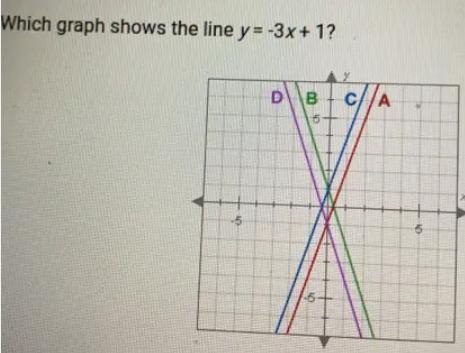
Which graph shows the line y=-3x+1?
A. Graph A
B. Graph B
C. Graph C
D. Graph D
Answers
The graph that shows the line y = - 3 x + 1 would be B. Graph B.
How to find the graph ?To find the graph, you need to find the x and y values from the given equation of line y=-3x+1.
Then look at the graph that has these points.
For x = -2:
y = -3(-2) + 1
y = 6 + 1
y = 7
For x = -1:
y = -3(-1) + 1
y = 3 + 1
y = 4
For x = 0:
y = -3(0) + 1
y = 0 + 1
y = 1
For x = 1:
y = -3(1) + 1
y = -3 + 1
y = -2
For x = 2:
y = -3(2) + 1
y = -6 + 1
y = -5
For x = 3:
y = -3(3) + 1
y = -9 + 1
y = -8
So, the y values for x = -3 to x = 3 are:
x = -3: y = 10
x = -2: y = 7
x = -1: y = 4
x = 0: y = 1
x = 1: y = -2
x = 2: y = -5
x = 3: y = -8
The graph that has these points is therefore Graph B.
Find out more on graphs at https://brainly.com/question/14474675
#SPJ1