2) If r=9, b=5, g=-6 , what does (r+b-g)(b+g) equal? A)-20 B) -8 C)8 D)19 E)20
Answers
Work Shown:
(r+b-g)(b+g)
(9+5-(-6))(5-6)
(9+5+6)(5-6)
(20)(-1)
-20
Related Questions
PLEASE HELP!!!!! i am desperate.
Zack is building a model sailboat. The mast will have two inches of height below the base of the main sail, as shown in the diagram below. He wants the base of the sail to have a length of 11 inches and angle S to measure 49 degrees.
A) Write an equation that can be used to find the length of the side of the triangular sail opposite angle S.
B) Find the length of the side of the triangle opposite angle S, to the nearest tenth.
C) What will be the height of the mast, to the nearest tenth?

Answers
Answer:
A) x = 11 tan 49°
B) 12.7 inches
C) 14.7 inches
Step-by-step explanation:
(refer to attached for reference)
Let the length of the vertical side of the triangular sail be x
recall that for right angle triangle, the following trigonometric relation applies:
tan θ = length of opposite side / length of adjacent side
in our case,
θ = 49°
length of adjacent side = 11 inches
length of opposite side = length of vertical edge of sail = x (which we defined above)
hence we can assemble our formula
tan 49° = x / 11 (rearranging)
x = 11 tan 49° (Answer for A)
Using a calculator to solve this gives
x = 12.65 inches
x = 12.7 inches (to nearest tenth) (Answer for B)
The height of the mast is merely the height of the sail plus the 2" length of mast extending below the sail.
Mast height = 12.7" + 2" = 14.7" (Answer for C)

Kindly solve the following with the cirrect method .SOLVE ALL . I'll give brainliest + thanks + follow

Answers
The following percentages are listed below:
12.5 %40 %6.25 %6.667 %41.667 %75 %How to use percentages in real life situationsIn this question we have seven cases of real life situations in which percentages are used. Mathematically speaking, percentages are represented by the following expression:
x = r / r' × 100 (1)
Where:
r - Real quantityr - Maximum quantityNow we proceed to determine quantities related to percentages:
2.8 mm as a per cent of 2.24 cm
x = (2.8 mm / 22.4 mm) × 100 %
x = 12.5 %
What per cent of 1.5 m is 60 cm?
x = (60 cm / 150 cm) × 100 %
x = 40 %
What per cent of 2 kg is 125 g?
x = (125 g / 2000 g) × 100
x = 6.25 %
What per cent of R 6 to 40 p?
x = (40 / 600) × 100
x = 6.667 %
What per cent of a day is 10 h?
x = (10 h / 24 h) × 100
x = 41.667 %
What per cent of 7 1 / 3 m in 5 1 / 2 m ?
x = [(11 / 2) / (22 / 3)] × 100 %
x = 75 %
To learn more on percentages: https://brainly.com/question/14979505
#SPJ1
Find one value of x that is a solution to the equation:
(4x + 1)^2 + 9(4x + 1) = -18
x =
Answers
Answer:
There are two solutions
1: -7/4
2: -1
Step-by-step explanation:
Hope this helps
Brain-List?
y is inversely proportional to the cube of x if y = 7 when x=4 what is y when x is 5
Answers
Answer:
8.75
Step-by-step explanation:
7/4 = 1.75 and ?/5 (5x1.75) = 8.75
Marco wants to know how much the other students in his mathematics class study. He recorded the data he collected in
the following table.
Time spent studying per week (in hours)
2.0
5.0
1.0
2.5
2.5
3.5
0.0
4.5
2.5
4.0
3.5
3.0
2.0
1.5
4.0
2.0
0.5
3.0
1.0
3.0
3.5
1.5
1. Construct a histogram for the data.

Answers
Answer:
Step-by-step explanation:
This problem has been solved! You'll get a detailed solution from a subject matter expert that helps you learn core concepts.
For Mean = 73.19, Mode = 79.56 and Variance = 16, the Karl Pearson's Coefficient of Skewness will be -0.0256 -1.64 0.0256 0
Answers
Answer:
To calculate Karl Pearson's coefficient of skewness, we need to use the formula:
Skewness = 3 * (Mean - Mode) / Standard Deviation
Given the Mean = 73.19, Mode = 79.56, and Variance = 16, we need to find the Standard Deviation first.
Standard Deviation = √Variance = √16 = 4
Now we can substitute the values into the formula:
Skewness = 3 * (73.19 - 79.56) / 4
Skewness = -6.37 / 4
Skewness = -1.5925
Rounded to four decimal places, the Karl Pearson's coefficient of skewness for the given values is approximately -1.5925.
Los puntos A(13, a) y B (4,b) pertenecen a una parábola de vértice V (h, 1) Además el eje focal es paralelo al eje de las abscisas ,su parámetro es p y A, B están
contenidos en la recta 2x - y - 13 = 0. Hallar a" + bP.
Answers
The points on a parabola with the focal axis parallel to the abscissa axis, of parameter p and A, B is -12.
How to calculate parameters?Since A and B are points on the parabola, write two equations using the general form of the parabolic equation:
(x - h)² = 4p(y - 1)
The focal axis is parallel to the x-axis, so the distance from the vertex to the focus is equal to p. Therefore, use the distance formula to write an equation for the distance between the vertex and point A:
√((13 - h)² + (a - 1)²) = p
Similarly, write an equation for the distance between the vertex and point B:
√((4 - h)² + (b - 1)²) = p
A and B lie on the line 2x - y - 13 = 0, so substitute the x and y coordinates of A and B into this equation and solve for a and b:
2(13) - a - 13 = 0
2(4) - b - 13 = 0
Solving these equations gives us a = 3 and b = -5.
Now three equations and three unknowns (a, b, and h):
√((13 - h)² + 4) = p + 1
√((4 - h)² + 36) = p + 1
2h - 3 - 13 = 0
The third equation simplifies to 2h = 16, or h = 8.
Substituting this value of h into the first two equations and squaring both sides:
(13 - 8)² + 4 = (p + 1)²
(4 - 8)² + 36 = (p + 1)²
Simplifying these equations and solving for p gives us p = 3.
Finally, find a" + bP by substituting the values found for a, b, and p:
a" + bP = 3 + (-5)(3) = -12
Therefore, the solution is a" + bP = -12.
Find out more on parabola here: https://brainly.com/question/25651698
#SPJ1
Can anyone tell me What is 95% of 75
Answers
Answer:
Also could you mark my answer as brainliest? It helps and doesnt hurt
In 2015, the average distance from Earth to the moon was about 3.74 x 105 km. The distance from Earth to Mars was about 9.25 x 107 km. How much farther is traveling from Earth to Mars than from Earth to the moon? Write your answer in scientific notation.
Answers
Traveling from Earth to Mars is approximately 9.249626 x 10^7 km farther than traveling from Earth to the moon.
Earth to Mars is compared to traveling from Earth to the moon, we need to calculate the difference between the distances.
The distance from Earth to the moon is approximately 3.74 x 10^5 km.
The distance from Earth to Mars is approximately 9.25 x 10^7 km.
To find the difference, we subtract the distance to the moon from the distance to Mars:
9.25 x 10^7 km - 3.74 x 10^5 km
To subtract these numbers, we need to make sure the exponents are the same. We can rewrite the distance to the moon in scientific notation with the same exponent as the distance to Mars:
3.74 x 10^5 km = 0.374 x 10^6 km (since 0.374 = 3.74 x 10^5 / 10^6)
Now we can perform the subtraction:
9.25 x 10^7 km - 0.374 x 10^6 km = 9.25 x 10^7 km - 0.374 x 10^6 km
To subtract, we subtract the coefficients and keep the same exponent:
9.25 x 10^7 km - 0.374 x 10^6 km = 9.25 x 10^7 - 0.374 x 10^6 km
Simplifying the subtraction:
9.25 x 10^7 - 0.374 x 10^6 km = 9.249626 x 10^7 km
Therefore, traveling from Earth to Mars is approximately 9.249626 x 10^7 km farther than traveling from Earth to the moon.
Scientific notation is a convenient way to express very large or very small numbers. It consists of a coefficient (a number between 1 and 10) multiplied by a power of 10 (exponent). It allows us to write and manipulate such numbers in a compact and standardized form.
To know more about Traveling .
https://brainly.com/question/21219866
#SPJ11
Students at a local community college have G.P.A.s that are normally distributed with a mean of 2.8 and a standard deviation of 0.5.
Answers
The percentage of students at the college have a GPA between 2.3 and 3.3 is C. 68.26%.
How to calculate the percentage?How far is 2.3 from 2.8. This will be:
= (2.3-2.8) = -0.5
That means 2.3 is one standard deviation to the left of the mean.
How far is 3.3 from 2.8? This is (3.3-2.8) = 0.5
That means 3.3 is one standard deviation to the right of the mean.
According to the empirical rule 68% of normally distributed data is within 1 standard deviation of the mean.
Therefore, the correct option is C.
Learn more about normal distribution on:
https://brainly.com/question/4079902
#SPJ1
At one college GPA's are normally distributed with a mean of 2.8 and a standard deviation of .5. What percentage of students at the college have a GPA between 2.3 and 3.3?
a)84.13% b)99.74% c) 68.26% d) 95.44%
HELP ME raaaaaaaa NOWWWWWWWWWW

Answers
Answer:
C: EAF Is the correct answer
The phone company Splint has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses 390 minutes, the monthly cost will be $178. If the customer uses 940 minutes, the monthly cost will be $398.
find an equation in the form y=mx+b, where x is the number of monthly minutes and y is the total monthly of the splint plan.
B) Use your equation to find the total monthly cost if 866 minutes are used.
Answer: If 866 minutes are used, the total cost will be dollars.

Answers
Therefore , the solution of the given problem of equation comes out to be total cost for 866 minutes is $1487.
What is an equation?The similar symbol (=) is used in arithmetic equations to signify equality between two statements. It is shown that it is possible to compare various numerical factors by applying mathematical algorithms, which have served as expressions of reality. For instance, the equal sign divides the number 12 or even the solution y + 6 = 12 into two separate variables many characters are on either side of this symbol can be calculated. Conflicting meanings for symbols are quite prevalent.
Here,
Given :
customer uses 390 minutes , the monthly cost will be $178.
customer uses 940 minutes, the monthly cost will be $398.
To find an equation ,
where x is number of monthly minutes
and y is total monthly of splint plan.
So , equation is :
=> y =mx +b
For first case :
=> 178 = 390x + b
Second case :
=> 398 = 940x + b
Solve for x:
=> 178 - 390x = 398 - 940x
=> -200x = - 550
=> x = 550/200
=>x = 55/20
=>x = 11/4
=> x = 2.75
For value of b
=> 178 = 390(2.75) + b
=> 178 - 1072.5 = b
=> -894.5 = b
B)
=> y = 866(2.75) - 894.5
=> y = 2381.5 - 894.5
=> y = 1487
Therefore , the solution of the given problem of equation comes out to be total cost for 866 minutes is $1487.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
An elementary school is offering 3 language classes: one in Spanish, one in French, and one in German. These classes are open to any of the 100 students in the school. There are 28 students in the Spanish class, 21 in the French class, and 12 in the German class. There are 9 in both Spanish and French, 5 in both Spanish and German, and 5 that are in both French and German. There are 3 students taking all 3 classes.
Required:
a. If a student is chosen randomly, what is the probability that he or she is not in any of the language classes?
b. If a student is chosen randomly, what is the probability that he or she is taking exactly one language class?
c. If 2 students are chosen randomly, what is the probability that at least 1 is taking a language class?
Answers
Answer:
0.55 ; 0.32 ; 0.7
Step-by-step explanation:
Let :
Spanish = S ; French = F ; German = G
SnFnG = 3
(SnF) only = 9 - 3 = 6
(SnG) only = 5 - 3 = 2
(FnG) only = 5 - 3 = 2
S only = 28 - (6+3+2) = 17
F only = 21 - (2+3+2) = 14
G only = 12 - (6+3+2) = 1
Student not taking any of the classes :
(100 - (17+14+1+2+2+6+3))
100 - 45 = 55
A.) P(not taking any language class).
Required outcome = 55
Total possible outcomes = 100
= 55 / 100 = 0.55
B.)
P(taking exactly one language class)
(S only + F only + G only) / 100
(17 + 14 + 1) / 100
= 32/100
= 0.32
C.)
Atleast 1 is taking a language class out of 2 selected
Possibilities :
(taking and not taking) ;
(not taking and taking) ;
(taking and taking)
(45/100 * 55/99) + (55/100 * 45/99) + (45/100 * 44/99) = 0.7
there was 506 tickets sold for the school play they were either student tickets or adult tickets there was 56 more student tickets sold than adult tickets sold how many adult tickets were sold
Answers
Answer:
A = 228 tickets
Step-by-step explanation:
We need to set up a system of equation to find the number of adult tickets sold, where A represents the adult tickets and S represents the student tickets.
Because the number of adult and student tickets together equals 506, we have A + S = 506.
Because there are 56 more student tickets than adult tickets we have A + 56 = S
And the way the system is already set up allows us to use substitution.
Thus, we have:
\(A + S=506\\A+56 = S\\\\A+A+56 =506\\2A+56=506\\2A=456\\\\A=228\\228+56=S\\278=S\)
The number of student tickets was not necessary to find in this problem, but I found anyway just in case you wanted check the work or wanted to prove the validity of the values.
Please answer ASAP I will brainlist
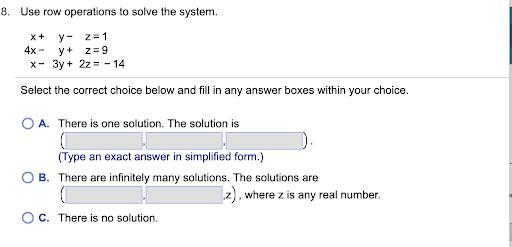
Answers
Answer:
There is one solution. The solution is 2, 18, 19.
Step-by-step explanation:
If you want me to show working tell me in the comments and I'll edit the answer
Answer:
A. (2, 18, -19)
Step-by-step explanation:
To solve:
Z is the most suitable variable to remove first
Add the first equation to the second equation: (this conveniently removes both y and z)
(x+y-z) + (4x-y+z) = 1+9
Simplify
5x = 10
Solve
x = 2
Multiply the second equation by 2 and minus it to the third equation: (Solve for y)
2(4x-y+z) - (x-3y+2z) = 2(9) - (-14)
Simplify
8x-2y+2z-x+3y-2z=18+14
7x+y=32
Substitute using x=2
7(2) + y = 32
y = 32 - 14
y = 18
Now substitute x and y for their respective values into Equation 1
2 + (-18) - z = 1
Simplify
-z = 19
z = -19
So :
x = 2, y = 18 , z = -19
21 plus 22 plus 9 plus 10 times zero
Answers
Answer:
52
Step-by-step explanation:
Also Written as:
((21+22)+9)+(10*0)
Using the PEMDAS also known as Order of operations.
((21+22)+9)+(10× 0) {10× 0 = 0}
((21+22)+9)+(0)
Then, it will look like this below:
((21+22)+9)
Now add then all together..
21 + 9 = 30
30 + 22 = 52
Input Equation:
Input Equation:
= ((21+22)+9)+(10*0)
= ((43)+9)+(10*0)
= (43+9)+(10*0)
= (52)+(10*0)
= 52+(10*0)
= 52+(0)
= 52+0
= 52
Hence, the answer is 52.
[RevyBreeze]
3. Divide 41 by 15. Give your answer to 3 decimal places
Answers
We have the following:
Therfeore, the answer is 2,733

find a solution y = 3 x − 4
Answers
Answer: The equation y = 3x - 4 is a linear equation in slope-intercept form, where the slope (3) is the coefficient of x and the y-intercept (-4) is the constant term. To find a solution for this equation, we can substitute a specific value of x and solve for the corresponding value of y.
For example, if we let x = 2, we can substitute it into the equation:
y = 3(2) - 4 = 6
So the solution for x=2 is y=6
We can also graph this equation, it will be a straight line with slope 3 and y-intercept (-4)
Step-by-step explanation:
WILL MAKE BRAINLIEST
write the slope intercept form of the equation of each line

Answers
Answer:
3. y = -3x + 2
4. y = 3x - 5
Step-by-step explanation:
Slope-intercept form equation is given as y = mx + b.
3. First, using two points on the line, (0, 2) and (1, -1), find the slope (m).
Slope (m) = change in y / change in x = (-1 - 2)/(1 - 0) = -3/1
m = -3
Find the y-intercept (b):
The y-intercept (b) = 2 (this is where the line intercepts the y-axis)
b = 2
✅To write the equation, substitute m = -3 and b = 2 into y = mx + b
Thus:
y = -3x + 2
4. Using two points on the line, (2, 1) and (0, -5), find the slope (m).
Slope (m) = change in y / change in x = (-5 - 1)/(0 - 2) = -6/-2 = 3
m = 3
Find the y-intercept (b):
The y-intercept (b) = -5 (this is where the line intercepts the y-axis)
b = -5
✅To write the equation, substitute m = 3 and b = -5 into y = mx + b
Thus:
y = 3x + (-5)
y = 3x - 5
Find two vectors in opposite directions that are orthogonal to the vector u. (There are many correct answers.)

Answers
Given:
The given vector is u=<7,9>.
Required:
We need to find two vectors in opposite directions that are orthogonal to the vector u.
Explanation:
Recall that two vectors are orthogonal if their dot product equals 0.
Let v be the orthogonal vector to u.
\(u\cdot v=0\)\(<7,9>\cdot=0\)\(7v_1+9v_2=0\)\(7v_1+9v_2-9v_2=-9v_2\)\(7v_1=-9v_2\)\(\frac{7v_1}{7}=\frac{-9v_2}{7}\)\(v_1=-\frac{9}{7}v_2\)\(v=<-\frac{9}{7}v_2,v_2>\)\(Let\text{ }v_2=7\text{ and substitute in the vector v.}\)\(v=<-\frac{9}{7}\times7,7>=<-9,7>\)\(Let\text{ }v_2=-7\text{ and substitute in the vector v.}\)\(v=<-\frac{9}{7}\times(-7),-7>=<9,-7>\)Final answer:
\(negative\text{ x-component, positive y-component=<-9,7>}\)\(positive\text{ x-component, negative y-component=<9,-7>}\)the metric that measures the percentage of the total number of items on an order that a firm shipped on time is. is the meaning of?
Answers
Unit Fill Rate: The percentage of a customer's purchase that was shipped on time. This statistic calculates the quantity and time elapsed after the order was dispatched, rather than when the client made the purchase.
On-time delivery is a key performance indicator (KPI) used by ecommerce and other delivery organizations to evaluate their ability to complete a client purchase by the specified delivery date.
The metric used to quantify supply chain efficiency is on-time delivery, or OTD. This KPI indicates whether or not an organization is meeting its goals in terms of promised delivery times, and it is critical for measuring carrier performance as well as maintaining customer satisfaction.
Learn more about to measures the percentage visit here;
https://brainly.com/question/14126037
#SPJ4
Which answer is not correct?

Answers
Answer:
the third choice
Step-by-step explanation:
because j is not a angle it is part of a angle
If there are 624 calories in 3 servings, how many calories are in 1 serving
Answers
Answer:
208 calories
Step-by-step explanation:
You have to divide 624 by 3, and you get 208.
Type the correct answer in each box. Use numerals instead of words.
Consider function h.
What are the values of the function when x= 0 and when x=4
h(0)=
h(4)=

Answers
Answer:
10 16
Step-by-step explanation:
when x= 0 h(x)=2x²-3x+10
⇒ h(0)=2*0²-3*0+10=10
when x= 4 h(x)=\(2^{x}\)
⇒ h(4)=\(2^{4}\)=16
The value of the given piecewise function at \(x=0\) is \(h(0)=10\) and the value of the function at \(x=4\) is \(h(4)=16\).
Important information:
The given piecewise function is:\(h(x)=\begin{cases}3x-4, &x < 0 \\ 2x^2-3x+10, &0\leq x < 4 \\ 2^x, & x\geq 4\end{cases}\)
Piecewise Function:The function for \(x=0\) is \(h(x)=2x^2-3x+10\).
\(h(0)=2(0)^2-3(0)+10\)
\(h(0)=10\)
The function for \(x=4\) is \(h(x)=2^x\).
\(h(4)=2^4\)
\(h(4)=16\)
Therefore, the required values of the piecewise function are \(h(0)=10\) and \(h(4)=16\).
Find out more about 'Piecewise Function' here:
https://brainly.com/question/17966003
SP bisects _RST. Find the following. m please help as soon as possible!!!!! thank you

Answers
1) To better visualize it let's draw that bisected angle
According to the Bisector theorem, those angles are congruent therefore we can write an equation:
3x-2=9x-26
-2+26=9x-3x
24=6x
6x=24
x=4
m RST = (3x -2) + (9x -26)
m RST = 3(4) -2 +9(4) -26
m RST = 12 -2 +36 -26
m RST = 10 +10
mRST = 20º

15 POINTS
Using Pythagoras' theorem, calculate the length
of XY.
Give your answer in centimetres (cm) to 1 d.p.

Answers
Answer:
13.27 cm
Step-by-step explanation:
I am using (xy) to mean the length of the side xy
7^2 + (xy)^2 = 15^2
49 + (xy)^2 = 225
(xy)^2 = 225-49
(xy)^2 = 176
Side (xy) = sqrt(176) = 13.2664991614 = 13.27 cm
13.3cm
Step-by-step explanation:
The Pythagorean theorem is a^2+ b^2 = c^2
Plug the values into the equation.
7^2+ b^2 = 15^2
Simplify.
49 ÷ b^2 = 225
Subtract 49 from both sides.
b^2 = 176
Take the square root of both sides.
vb^2 = v176
b=13.266
b=13.3cm
A traveler standing at the intersection of Green Avenue and Wyoming Street wants to walk to the State Building. The traveler knows that the State Building is 8 blocks from the intersection of Orovada Street and Washington Avenue. She also knows that the intersection of Orovada Street and Washington Avenue is 5 blocks from the intersection of Wyoming Street and Washington Avenue. If the traveler had to walk 4 blocks to get from the intersection of Wyoming Street and Green Avenue to the intersection of Orovada Street and Green Avenue, how much further must she walk to reach the State Building?
Answers
The traveler must walk 17 blocks to reach the State Building.
Solving for how much further must she walk to reach the State Building:The traveler needs to walk 8 blocks from the intersection of Orovada Street and Washington Avenue to the State Building.
She also knows that the intersection of Orovada Street and Washington Avenue is 5 blocks from the intersection of Wyoming Street and Washington Avenue, so she needs to walk 5 blocks from the intersection of Wyoming Street and Washington Avenue to the intersection of Orovada Street and Washington Avenue.
Also, the traveler had to walk 4 blocks to get from the intersection of Wyoming Street and Green Avenue to the intersection of Orovada Street and Green Avenue.
Therefore, the traveler must walk 8 + 5 + 4 = 17 blocks to reach the State Building.
Learn more about quantitative Reasoning on
https://brainly.com/question/15566375
#SPJ1
Factor −5x2 + 10x.
PLS HURRY NEED THIS DUE TODAY
Answers
Answer:
C. 5x(-x + 2)
Step-by-step explanation:
To factor the expression -5x² + 10x, we need to look for a common factor that can be factored out.
Finding a common factor involves identifying a term or expression that can be factored out from each term of a given expression.
Both terms have the common factor of 5x, so we can factor out 5x:
5x(-x + 2)
Therefore, the factored form of -5x² + 10x is -5x(x - 2).
\(\hrulefill\)
Additional notes:
If we expand the expressions in the given answer options, we get:
A. −5x(x + 2) = -5x² - 10x
B. 5(−x² + 10x) = -5x² + 50x
C. 5x(−x + 2) = -5x² + 10x
D. x(5x + 10) = 5x² + 10x
Hence confirming that the correct answer is option C.
To factor \(-5x^2+10x\), we can begin by factoring out the greatest common factor, which is \(-5x\):
\(-5x^2 + 10x = \boxed{-5x(x - 2)}\)We can check our answer by distributing \(-5x\) to the expression inside the parentheses:
\(\begin{aligned}-5x(x - 2)& = (-5x)(x) + (-5x)(-2)\\& = -5x^2 + 10x\end{aligned}\)\(\therefore\) The answer is \(-5x(x-2)\).
\(\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}\)
Sully is having a party and wants to fill his swimming pool. If he only uses his hose, it takes 3 hours more than if he only uses his neighbor's hose. If he uses both hoses together, the pool fills in 5 hours. How long does it take for each hose to fill the pool (in hr)?
Answers
Answer:
It takes the neighor's hose 3 hours to fill the pool and it takes Sully's hose 6 hours to fill the pool if each filled alone.
Step-by-step explanation:
This is a work problem, and the way these are done is to figure the amount that each can do based on how much can get done in a single hour.
First thing, in order to have only one variable, we have to put one hose in terms of the other hose.
We know that it takes the neighbor's hose a certain amount of time (there's our unknown) to fill the pool and that it takes Sully's hose that same time plus 3 hours.
neighbor's hose can get the job done in x time
Sully's hose can get the job done in x + 3 time
Now we will figure out how much each can do in a single hour.
If the neighbor's hose takes x hours to fill the pool, then it can get
of the pool filled in 1 hour.
If Sully's hose takes x + 3 hours to fill the pool, then it can get
of the pool filled in 1 hour.
The sum of these takes 2 hours total and 1/2 of the pool gets filled in 1 hour.
Our equation then is:
This equation states in words:
"the amount of the pool that the neighbor's hose can fill in an hour plus the amount of the pool that Sully's hose can fill in an hour will fill half the pool".
Solving for x will give us that time.
Begin to solve this by finding the LCM of those denominators and getting rid of the fractions by reducing. The LCM will be 2x(x + 3). Multiplying each term by that LCD looks like this:
In the first term the x's cancel out, in the second term the (x + 3) cancels out, and in the last term the 2's cancel out leaving us with:
and simplifying gives us:
This is a quadratic that will have to be factored to solve for those values of x. Combine like terms and get everything on one side to get:
Factor this however you find easiest to get the values:
x = 3 hours and x = -2 hours
We all know that the 2 things in math that will never EVER be negative are times and distances/measures, so we can disregard the -2 and say that
x = 3 hours.
To answer our question, then;
It takes the neighbor's hose 3 hours to fill the pool; it takes Sully's hose 3+3 hours = 6 hours to fill the pool.
A right circular cone is intersected by a plane that passes through the cone's
vertex and is perpendicular to its base, as in the picture below. What is
produced from this intersection?
OA. A pair of parallel lines
B. A single line
OC. A point
OD. A pair of intersecting lines
Answers
Answer:
D. A pair of intersecting lines
Step-by-step explanation:
A conic section is a fancy name for a curve that you get when you slice a double cone with a plane. Imagine you have two ice cream cones stuck together at the tips, and you cut them with a knife. Depending on how you cut them, you can get different shapes. These shapes are called conic sections, and they include circles, ellipses, parabolas and hyperbolas. If you cut them right at the tip, you get a point. If you cut them slightly above the tip, you get a line. If you cut them at an angle, you get two lines that cross each other. That's what happened in your question. The plane cut the cone at an angle, so the curve is two intersecting lines. That means the correct answer is D. A pair of intersecting lines.
I hope this helps you ace your math question.