2/3 of a number is 12. What is 1/2 the number?
Answers
Answer:
Step-by-step explanation:
the number is 18, so half of that would be
Related Questions
write the sequence of natural numbers which leaves the remainder 3 on didvidng by 10
Answers
The sequence of natural numbers that leaves a remainder of 3 when divided by 10 is:
3, 13, 23, 33, 43, 53, 63, 73, 83, 93, 103, 113, ...
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Gabriel deposits $660 every month into an account earning a monthly interest rate of
0.475%. How much would he have in the account after 16 months, to the nearest
dollar? Use the following formula to determine your answer.

Answers
The future value of the monthly deposit which earns 0.475 monthly interest will be $10,944.67 after 16 months.
How the future value is determined:The future value can be determined using the future value annuity formula or an online finance calculator.
The future value represents the periodic deposits compounded periodically at an interest rate.
N (# of periods) = 16 months
I/Y (Interest per year) = 5.7% (0.475% x 12)
PV (Present Value) = $0
PMT (Periodic Payment) = $660
Results:
Future Value (FV) = $10,944.67
The sum of all periodic payments = $10,560.00
Total Interest = $384.67
Thus, using an online finance calculator, the future value of the monthly deposits is $10,944.67.
Learn more about the future value at https://brainly.com/question/24703884.
#SPJ1
does anyone know the answer to this

Answers
Answer:
1=27
2=65
3=115
4=
Step-by-step explanation:
I am still working on four i will put it in the comments
If f(x) = x2 – 3, then f(-1) is equivalent
to
Answers
Answer:
negative 5. or -5
Step-by-step explanation:
f(-1)= (-1)2-3
2 times -1= -2
-2-3= -5
f= -5
this question is -5
I need help as soon as possible

Answers
Answer:
A. x = 4
I hope this helps!
15 8 5 12 = 17 make it true
Answers
Answer:
take away the 15 and 8
Step-by-step explanation:
12 plus 5 =17
Answer:
15÷(8-5)+12=17
Step-by-step explanation:
Use PEMDAS to solve
15÷(8-5)+12=17
first-parentheses
(8-5)=3
rewrite equation
15÷3+12=17
next-divide
15÷3=5
rewrite equation
5+12=17
and finally-add
5+12=17
:)
Hope This Helps
(brainliest please, if possible)
Pilar used six reusable shopping bags on a recent purchase she made at a grocery store. Each bag decreased the amount she spent by 5 cents. What was the change to the amount Pilar spent at the grocery store by using the reusable bags?
A.
-30 cents
B.
11 cents
C.
30 cents
D.
-11 cents
Answers
Use the equation P = 10 -2.5c.
Find P when c = 3.2
Answers
Answer:
p=2
Step-by-step explanation:
3.2*2.5=8
10-8=2
PLEASE HELP ASAP WILL GIVE POINTS AND BRAINLIEST! TY BESTIES! Factor using GCF 20x^2+10x please show work
Answers
Answer:
10x(2x+1)
Step-by-step explanation:
20x^2+10x
2*10*x*x + 10 *x
Factor out the common terms
10x(2x+1)
Consider the polynomial p(x)=16x^4 - 81y^4. Which of the following are equivalent expressions?
Answers
Answer: (2x^2 - 3y^2)(2x^2 + 3y^2)(4x^2 + 9y^2)
Step-by-step explanation:
Formula to remind: \((A^2 - B^2) = (A-B)(A+B)\)
\(16x^4 - 81y^4 = (4x^2 - 9y^2)(4x^2 + 9y^2) = (2x^2 - 3y^2)(2x^2 + 3y^2)(4x^2 + 9y^2)\)
A researcher identifies college students as a group of interest to test her hypothesis.She then identifies a few local college students and selects a small group of local college students to be observed.In this example,the sample is:
A) not clearly identified.
B) all college students.
C) the few local college students.
D) the small group of college students who are observed.
Answers
The sample in this example is D) the small group of college students who are observed. The correct option is D.
The researcher has identified college students as her group of interest, but it is not feasible or practical to observe or study all college students. Therefore, she needs to select a subset of college students, which is known as a sample. In this case, she has chosen to observe a small group of local college students, which is the sample. It is important to note that the sample needs to be representative of the larger population of interest, in this case, all college students, in order for the results to be applicable to the larger group.
While the sample in this example is only a small group of local college students, the researcher would need to ensure that they are representative of all college students in order for the results to be generalizable.
To know more about sample visit:-
https://brainly.com/question/32277048
#SPJ11
Need Help here Please!

Answers
Answer:
Step-by-step explanation:

To solve the given equation \(\sf x - y = 4 \\\), we can perform the following calculations:
a) To find the value of \(\sf 3(x - y) \\\):
\(\sf 3(x - y) = 3 \cdot 4 = 12 \\\)
b) To find the value of \(\sf 6x - 6y \\\):
\(\sf 6x - 6y = 6(x - y) = 6 \cdot 4 = 24 \\\)
c) To find the value of \(\sf y - x \\\):
\(\sf y - x = - (x - y) = -4 \\\)
Therefore:
a) The value of \(\sf 3(x - y) \\\) is 12.
b) The value of \(\sf 6x - 6y \\\) is 24.
c) The value of \(\sf y - x \\\) is -4.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
I need a bit of help you don’t have to do all of them but put which # your doing please and thank you if you do answer all thank you

Answers
Answer:
1. 26
2. 15
3. 14
4. \(\sqrt{50}\) or \(5\sqrt{2}\)
5. \(\sqrt{11} \\\)
6. \(\sqrt{245}\) or \(7\sqrt{5}\)
I think most of these answers are correct
Find the equation of the line that i perpendicular to the line y=−3x5 and pae through the point (5,2)
Answers
The equation of the line is x - 3y + 1 =0.
What is the meaning perpendicular line?
A perpendicular is a straight line in mathematics that forms a right angle (90 degrees) with another line. In other words, two lines are perpendicular to one another if they connect at a right angle.
Given equation of line is
y=−3x + 5
Now compare the given equation with y = mx +c
m = -3 and c = 5.
The slope perpendicular line of the given line is = -1/m
= 1/3
The equation of line passes through the point (x₁, y₁) with slope m is
y - y₁ = m (x - x₁)
Putting m = 1/3, y₁ = 2, and x₁ = 5 in the above equation:
y - 2 = 1/3 (x - 5)
3y - 6 = x - 5
x - 3y + 1 =0
To learn more about equation of line, click on below link:
https://brainly.com/question/29524262
#SPJ4
Answer the problem below. Round your answer to the nearest tenth.
(1 decimal place)
A military cannon is placed at the base of a hill. The cannon is fired at an angle toward the hill. The path
of the cannon ball is parabolic and can be represented by y = -0.05x2 + 5x + 1, where y represents
the height of the ball in meters and x represents the horizontal distance of the ball from the cannon.
The incline of the hill can be represented by the equation y = 0.725x. How far will the cannon ball have
moved horizontal from the cannon when it hits the hill?
Answers
The cannonball will have moved approximately 24.2 meters horizontally from the cannon when it hits the hill.
To find the horizontal distance the cannonball travels before hitting the hill, we need to determine the point where the path of the cannonball intersects with the incline of the hill. We can do this by setting the equations of the cannonball's path and the incline of the hill equal to each other and solving for x.
Setting -0.05x^2 + 5x + 1 = 0.725x, we can rearrange the equation to form a quadratic equation: -0.05x^2 + 4.275x + 1 = 0.
Using the quadratic formula x = (-b ± √(b^2 - 4ac))/(2a), where a = -0.05, b = 4.275, and c = 1, we can solve for the two possible values of x.
Calculating the discriminant, b^2 - 4ac, we get 4.275^2 - 4(-0.05)(1) = 18.20625. Since the discriminant is positive, we have two real solutions.
Applying the quadratic formula, we find x ≈ -2.6 and x ≈ 24.2. Since we are interested in the positive value, the cannonball will have moved approximately 24.2 meters horizontally from the cannon when it hits the hill.
To learn more about equation click here: brainly.com/question/29657983
#SPJ11
The ratio of red marbles to blue marbles is 3:5. If there are 225 blue marbles total in the collection, how many of each color are there? Please show your work.
Answers
Answer:
Red balls = 84 Blue balls = 140
Step-by-step explanation:
Ok so there are 225 marbles
And ratio here is Red : Blue = 3 : 5
So Red marbles = 3x whereas Blue marbles = 5x
Therefore,
3x + 5x = 225
8x = 225
x = 28.125 = 28
Red balls = 28*3 = 84 Blue balls = 28*5 = 140
(Pls check whether total no of balls is 224)
Rachel went out for lunch. Her total for lunch came to $28.55. Rachel wants to leave the waitress a 22% tip. What will be Rachel's total including the tip?
Answers
Answer:
the answer is 6.28 her total is 34.83
Answer:
the answer is 6.28 hope it helps
Evaluate.
(a - 2b)^2 when a = -4 and b = -1/2
25
9
-9
-25
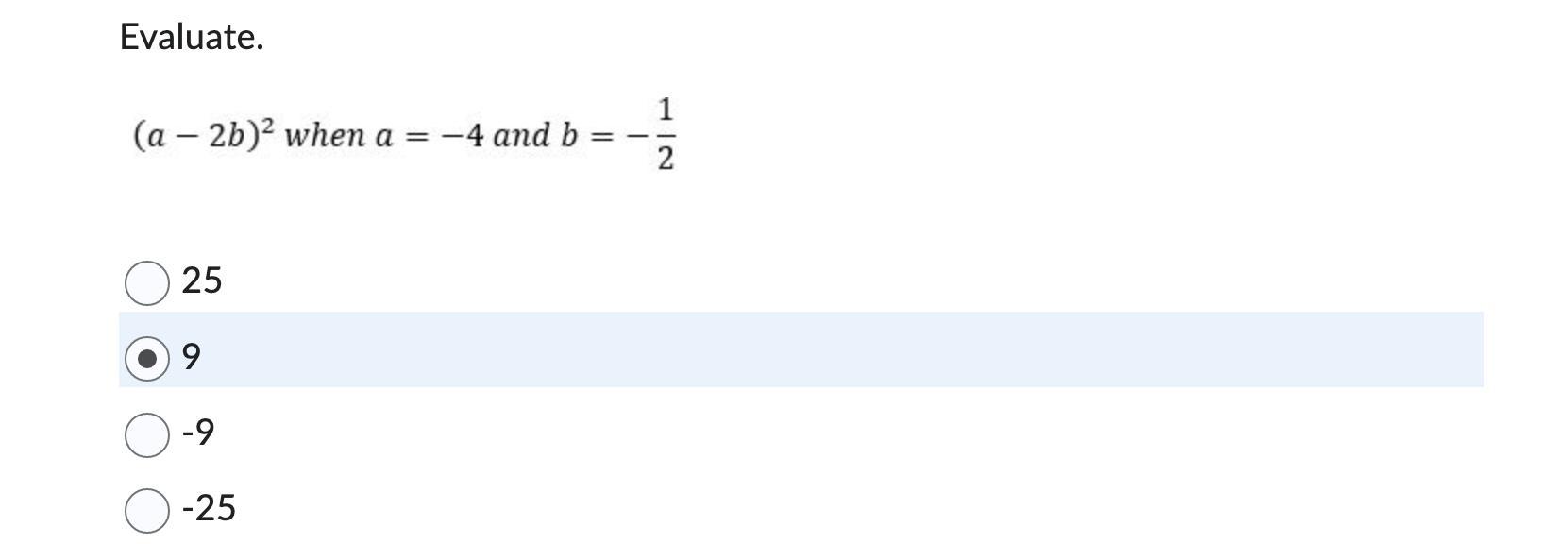
Answers
((-4)-2(-1/2))^2
Remember, when we have a squared binomial, it expands; do not distribute the exponents! So, if we have (a+b)^2, we do not distribute the exponent of 2 to a and b. Instead, we expand the binomial: (a+b)(a+b). The logic of exponents applies because a number times itself x time forms the exponent n^x.
[(-4)-2(-1/2)][(-4)-2(-1/2)]
Now, use PEMDAS to simplify:
Parenthesis/brackets first:
Multiplication and division come before addition and subtraction:
(-4+1)(4+1)
Simplify the parenthesis, then multiply:
(-3)(-3)
-3•-3 = 9
So, the answer is: 9
a successful proof can turn a conditional statement into a theorem.T/F
Answers
The given statement "A successful proof can indeed turn a conditional statement into a theorem.'' is true because a successful proof can transform a conditional statement into a theorem by providing a logical and rigorous demonstration of its truth based on the given hypothesis.
In mathematics, a conditional statement is a proposition that asserts a relationship between two or more mathematical objects or concepts. It consists of a hypothesis and a conclusion.
A conditional statement is typically expressed in the form "If A, then B," where A represents the hypothesis and B represents the conclusion.
To establish a conditional statement as a theorem, one needs to provide a valid proof that demonstrates the truth of the statement. A proof is a logical argument that follows a series of logical deductions from axioms, definitions, and previously established theorems.
When a proof is successfully constructed for a conditional statement, it provides rigorous justification for the truth of the conclusion based on the given hypothesis.
By demonstrating the logical validity and coherence of the argument, the proof confirms the truth of the conditional statement and establishes it as a theorem.
The process of proving a conditional statement involves carefully reasoning through logical steps, utilizing mathematical principles and logical inference rules.
It requires precise and accurate reasoning, ensuring that each step in the proof is valid and consistent with the underlying mathematical framework.
Once a conditional statement has been proven, it is elevated to the status of a theorem. Theorems are fundamental results in mathematics that have been rigorously proven and hold true within a given mathematical system.
They serve as building blocks for further mathematical investigations and form the foundation of mathematical knowledge.
In summary, a successful proof can transform a conditional statement into a theorem by providing a logical and rigorous demonstration of its truth based on the given hypothesis.
To know more about conditional statement refer here:
https://brainly.com/question/14457027#
#SPJ11
L 4.6.3 Test (CST): Linear Equations
me.
OA. y+4= -3(x-3)
OB. y-4=-3(x+3)
OC. y-4=3(x+3)
OD. y+4=3(x-3)
(3,-4)
Answers
The correct option is OA. y+4= -3(x-3). L 4.6.3 Test (CST): Linear Equations Solution: We are given that a line passes through (3,-4) and has a slope of -3.
We will use point slope form of line to obtain the equation of liney - y1 = m(x - x1).
Plugging in the values, we get,y - (-4) = -3(x - 3).
Simplifying the above expression, we get y + 4 = -3x + 9y = -3x + 9 - 4y = -3x + 5y = -3x + 5.
This equation is in slope intercept form of line where slope is -3 and y-intercept is 5.The above equation is not matching with any of the options given.
Let's try to put the equation in standard form of line,ax + by = c=> 3x + y = 5
Multiplying all the terms by -1,-3x - y = -5
We observe that option (A) satisfies the above equation of line, therefore correct option is OA. y+4= -3(x-3).
Thus, the correct option is OA. y+4= -3(x-3).
For more question on equation
https://brainly.com/question/17145398
#SPJ8
Hannah wants to buy a $540 camera. She can save $40 each week from her paycheck. However, before Hannah can buy the camera, she must give her brother $60 that she owes him. For how many weeks will Hannah need to save before she can pay back her brother and buy the camera?
Answers
Answer:
w = 12
Step-by-step explanation:
Create formula:
540 = 40w - 60 where 540 is the cost of the camera, 40 is the amount saved, w is the number of weeks, 60 is the amount owed
Solve for w
540 = 40w - 60: subtract 60
480 = 40w: divide by 40
w = 12
What is the equation of the line?
A: y = -4/5x + 3/2
B: y = -5/4x + 5/4
C: y = -4/5x + 5/4
D: y = -5/4x + 3/2

Answers
Answer:
A: y = -4/5x + 3/2 i believe is the correct answer
Step-by-step explanation:
Solve each system by elimination or substitution.
-x + 5y = 3 , 2x - 10y = 4
Answers
The given system of equations do not have a solution since their related line equations have the same slope.
The given system of equations is:
-x + 5y = 3 .......... (1)
2x - 10y = 4 ........(2)
In Equation (1), add both sides by (-5y)
-x + 5y + (-5y) = 3 + (-5y)
-x = -3 - 5y
Multiply by (-1)
x = 3 + 5y
Substitute x = 3 + 5y into equation (2)
2x - 10y = 4
2.(3 + 5y) - 10y = 4
6 + 10y - 10y = 4
6 = 4 (False)
Since the last equation is false, we might suspect that the given system of solution does not have solutions.
We need to check the slope of both equations:
-x + 5y = 3
⇒ 5y = x + 3
⇒ y = 1/5 x + 3/5
2x - 10y = 4
⇒ -10 y = -2x + 4
⇒ y = (2/10) x - 4/10
⇒ y = 1/5 x - 2/5
We can see that both equations have the same slope, i.e. 1/5.
Hence, they do not have solutions since the lines are parallel to each other.
Learn more on how to find solution of a system of equations here:
https://brainly.com/question/25869125
#SPJ4
Consider a wire in the shape of a
helix r(t)=2costi+2sintj+4tk,0≤t≤2π with
constant density function rho(x,y,z)=1.
A. Determine the mass of the wire: B. Determine the coordinates of the center of mass:
( , , )
C. Determine the moment of inertia about the
z-axis:
Answers
a. The mass of the wire is 4π√5.
b. The coordinates of the center of mass at (0, 0, 8π/3).
c. The moment of inertia about the z-axis is 16π√5.
A. To find the mass of the wire, we need to integrate the density function over the length of the wire:
M = ∫ρ(t)ds = \(\int\limits^{2\pi} _0\) ρ(t) ||r'(t)|| dt
where ||r'(t)|| is the magnitude of the derivative of r(t):
||r'(t)|| = ||-2sin(t)i + 2cos(t)j + 4k|| = √(4sin²(t) + 4cos²(t) + 16) = 2√5
Substituting in the values, we get:
M = \(\int\limits^{2\pi} _0\) 1 * 2√5 dt = 4π√5
Therefore, the mass of the wire is 4π√5.
B. The coordinates of the center of mass (x, y,z) can be found using the following formulas:
x = (1/M) ∫ρ(t)x(t)ds
y = (1/M) ∫ρ(t)y(t)ds
z = (1/M) ∫ρ(t)z(t)ds
We can simplify the expressions using the parameterization of the helix:
x(t) = 2cos(t)
y(t) = 2sin(t)
z(t) = 4t
Substituting the values, we get:
x = (1/4π√5) \(\int\limits^{2\pi} _0\) 2cos(t) * 2√5 dt = 0
y = (1/4π√5) \(\int\limits^{2\pi} _0\)2sin(t) * 2√5 dt = 0
z = (1/4π√5) \(\int\limits^{2\pi} _0\) 4t * 2√5 dt = 8π/3
Therefore, the center of mass is located at (0, 0, 8π/3).
C. The moment of inertia about the z-axis can be found using the formula:
Iz = ∫ρ(t)(x² + y²)ds
Using the same parameterization as before, we get:
Iz = \(\int\limits^{2\pi} _0\) 1 * (4cos²(t) + 4sin²(t)) * 2√5 dt
= \(\int\limits^{2\pi} _0\) 8√5 dt
= 16π√5
Therefore, the moment of inertia about the z-axis is 16π√5.
To learn more about density function, refer below:
brainly.com/question/31039386
#SPJ11
Consider the following data for a group of 2000 women. Of these women, 16 are known to have breast cancer. All 2000 undergo the same test to determine whether or not they have breast cancer, and 154 test positive. 14 of the 16 that have breast cancer test positive and 140 of those that do not have breast cancer test positive.
Find the probability that a woman has breast cancer given that her test result is positive.
Find the probability that a woman does not have breast cancer given that her test result is negative.
Answers
The probability that a woman tests positive given that she has breast cancer is 7/8 and the probability that a woman tests negative for breast cancer given that her test result is negative is 923/1000.
What is probability?Probability is the possibility of happening an event.
Since 14 of 16 have breast cancer test positive, the probability is:
p = 14/16
p = 7/8
Therefore, the probability that a woman tests positive given that she has breast cancer is 7/8.
The number of women who test negative is:
2000 - 154
= 1846
Therefore, 1846 out of 2000 women test negative.
The probability of a woman testing negative is:
p = 1846/2000
p = 923/1000
Therefore, The probability that a woman tests negative for breast cancer given that her test result is negative is 923/1000.
Learn more on probabilities here:
https://brainly.com/question/19557377
#SPJ1
At a nearby frozen yogurt shop, the mean cost of a pint of frozen yogurt is $1.50 with a standard deviation of $0.10.Assuming the data is normally distributed, approximately what percent of customers are willing to pay between $1.20 and $1.80 for a pint of frozen yogurt?
Answers
According to the question we have approximately 99.74 percent of customers are willing to pay between $1.20 and $1.80 for a pint of frozen yogurt.
To answer this question, we will use the normal distribution formula and z-score.
First, we need to find the z-score for the lower limit of $1.20:
z = (1.20 - 1.50) / 0.10 = -3
Next, we need to find the z-score for the upper limit of $1.80:
z = (1.80 - 1.50) / 0.10 = 3
Now, we can use a z-table to find the area under the curve between these two z-scores.
The area to the left of z = -3 is 0.0013, and the area to the left of z = 3 is 0.9987.
To find the area between these two z-scores, we subtract the area to the left of z = -3 from the area to the left of z = 3:
0.9987 - 0.0013 = 0.9974
Therefore, approximately 99.74% of customers are willing to pay between $1.20 and $1.80 for a pint of frozen yogurt.
To know more about Percent visit :
https://brainly.com/question/31323953
#SPJ11
write the fraction
28
32
in simplest form.
Answers
Answer: 7/8 or 0.875
Step-by-step explanation:
28
32
Reduce the fraction
28/32
to lowest terms by extracting and canceling out 4.
7/8
the simplest form of given fraction 28/32 is 7/8.
Given that:
Fraction: 28/32
To write the fraction 28/32 in its simplest form, to find the greatest common divisor (GCD) of the numerator (28) and the denominator (32) and then divide both the numerator and denominator by that GCD.
Step 1: Find the GCD of 28 and 32.
The factors of 28 are 1, 2, 4, 7, 14, and 28.
The factors of 32 are 1, 2, 4, 8, 16, and 32.
The largest common factor between 28 and 32 is 4.
Step 2: Divide both the numerator and denominator by the GCD (4).
28 ÷ 4 = 7
32 ÷ 4 = 8
Hence, the simplified fraction is 7/8.
Learn more about Fraction here:
https://brainly.com/question/10354322
#SPJ6
(-9) 4 as a exponent
Answers
Answer:
\(9^4\) = \(6561\)
in a school orchestra, 2/5 o the students are string players of the string players 5/8 are girls what fractin of all the stuentd in the orchestra are girls who play string instruments.
Answers
1/4 of all the students in the orchestra are girls who play string instruments.
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants.
Let's assume there are a total of 100 students in the school orchestra. Then, according to the problem, 2/5 of them are string players.
The number of string players is:
2/5 x 100 = 40
Out of these 40 string players, 5/8 are girls.
The number of girls who play string instruments is:
5/8 x 40 = 25
Therefore, the fraction of all the students in the orchestra who are girls who play string instruments is:
25/100 = 1/4
Therefore, 1/4 of all the students in the orchestra are girls who play string instruments.
To learn more about Algebraic expression from given link.
https://brainly.com/question/28884894
#SPJ1
Select the correct answer.
An insurance data scientist is researching a certain stretch of a rural highway where drivers are never pulled over. The mile markers in the solution of the following inequality determines the conclusion of his research.
Solve and interpret the compound inequality, where x represents the mile marker along the highway.
2x − 18 ≥ 122 or 5x + 15 < 250
Drivers located below mile marker 47 or at mile marker 70 or above never get pulled over.
Drivers located between mile marker 46 and mile marker 71 never get pulled over.
Drivers located below mile marker 46 or at mile marker 71 or above never get pulled over.
Drivers located between mile marker 47 and mile marker 70 never get pulled over.
Answers
The correct interpretation regarding the solution of the compound inequality is given as follows:
Drivers located below mile marker 47 or at mile marker 70 or above never get pulled over.
How to solve a compound inequality involving the or operation?To solve a compound inequality involving the or operation, we solve each inequality, then apply the union operation to their solutions.
In this problem, the following inequalities help us find the miles x in which the drivers are never pulled over.
2x - 18 ≥ 122.5x + 15 < 250.The solutions are found as follows:
2x - 18 ≥ 122
2x ≥ 140
x ≥ 140/2
x ≥ 70.
5x + 15 < 250.
5x < 235
x < 235/5
x < 47.
Hence the correct option is given by:
Drivers located below mile marker 47 or at mile marker 70 or above never get pulled over.
More can be learned about compound inequalities at https://brainly.com/question/24528399
#SPJ1