24-3x=-6x+22
Please answer x as a fraction
Answers
Answer:
I believe if you have a letter with no value or the value is unknown you put it over 1
Answer:
x = -2/3
Step-by-step explanation:
24 - 3x = -6x + 22
solve using inverse operations
24 - 3x = -6x + 22
+ 6x + 6x
24 + 3x = 22
-24 -24
3x = -2
/3 /3
x = -2/3
Related Questions
Consider three pallet locations A, B, and C, for which the travel time from the receiving area to the storage area is 1, 2, and 2 minutes, respectively. Two skus move through these locations, x and y, which must be managed strictly through a PEPS policy. Every three days a pallet of SKU "x" is dispatched in the morning and a pallet is received in the afternoon and stored. Every two days a pallet of SKU "y" is dispatched in the morning and a pallet is received in the afternoon and stored. You maintain a constant inventory of one pallet of SKU x and two pallets of SKU y at all times.
a. If you are using a static storage policy, what is the allocation of SKUs to storage locations that minimizes labor? Justify your answer. What is the average number of minutes per day spent moving these products?
b. What is the lowest value of average minutes per day used to move these SKUs if you adopt a heap policy? Does it make a difference where I place the SKUs initially?
Answers
A. The average number of minutes per day spent moving these products using the static storage policy is 1.33 minutes.
B. The lowest value of average minutes per day used to move these SKUs with the heap policy is approximately 1.17 minutes per day. The initial placement of the SKUs does make a difference in determining the lowest average movement time, as shown by the difference between Scenario 1 and Scenario 2.
a. Static Storage Policy:
To minimize labor, we can allocate the SKUs to storage locations based on their respective travel times from the receiving area to the storage area. In this case, the travel times are 1 minute for location A, 2 minutes for location B, and 2 minutes for location C.
Given that we maintain a constant inventory of one pallet of SKU x and two pallets of SKU y at all times, we can allocate them as follows:
SKU x: Allocate it to the storage location with the shortest travel time, which is location A (1 minute).
SKU y: Allocate both pallets to the storage location with the next shortest travel time, which is location B or C (both have a travel time of 2 minutes).
By allocating SKU x to location A and both pallets of SKU y to either location B or C, we ensure that the SKUs are stored in the closest available locations, minimizing the travel time needed to move them.
The average number of minutes per day spent moving these products can be calculated by considering the dispatch and receiving schedule:
SKU x: Dispatched every three days. Assuming it takes 1 minute to move a pallet from storage to the receiving area, the average daily movement time for SKU x would be (1/3) minutes per day.
SKU y: Dispatched every two days. Assuming it takes 2 minutes to move a pallet from storage to the receiving area, the average daily movement time for SKU y would be (2/2) minutes per day.
Adding up the average daily movement times for SKU x and SKU y, we get:
Average daily movement time = (1/3) + (2/2) = 1.33 minutes per day.
Therefore, the average number of minutes per day spent moving these products using the static storage policy is 1.33 minutes.
b. Heap Policy:
The heap policy involves storing the most frequently dispatched SKU closest to the receiving area. In this case, SKU y is dispatched every two days, while SKU x is dispatched every three days.
To find the lowest value of average minutes per day used to move these SKUs with the heap policy, we need to consider the different initial placements of the SKUs.
Scenario 1: Initial Placement - Location A for SKU x and Location B for SKU y
SKU x: Travel time from storage to the receiving area = 1 minute
SKU y: Travel time from storage to the receiving area = 2 minutes
Average daily movement time:
SKU x: (1/3) minutes per day
SKU y: (2/2) minutes per day
Total average daily movement time = (1/3) + (2/2) = 1.33 minutes per day
Scenario 2: Initial Placement - Location A for SKU y and Location B for SKU x
SKU y: Travel time from storage to the receiving area = 1 minute
SKU x: Travel time from storage to the receiving area = 2 minutes
Average daily movement time:
SKU y: (1/2) minutes per day
SKU x: (2/3) minutes per day
Total average daily movement time = (1/2) + (2/3) ≈ 1.17 minutes per day
Therefore, the lowest value of average minutes per day used to move these SKUs with the heap policy is approximately 1.17 minutes per day. The initial placement of the SKUs does make a difference in determining the lowest average movement time, as shown by the difference between Scenario 1 and Scenario 2.
Learn more about lowest value from
https://brainly.com/question/30236354
#SPJ11
use laplace transforms to solve the following initial value problem. 20, y0, x(0)0, y(0)
Answers
To solve the given initial value problem using Laplace transforms, we can apply the Laplace transform to both sides of the differential equation and use initial conditions to determine the transformed equation.
By algebraically manipulating the transformed equation, we can find the Laplace transform of the desired solution. Finally, we can use the inverse Laplace transform to obtain the solution in the time domain. Let's denote the unknown function as x(t). Applying the Laplace transform to both sides of the differential equation yields the transformed equation in terms of the Laplace transform variables s and X(s). By substituting the initial conditions x(0) = 0 and x'(0) = 20 into the transformed equation, we can solve for X(s).
After obtaining the Laplace transform X(s), we can manipulate the equation algebraically to isolate X(s) on one side. This may involve factoring, simplifying, and using partial fraction decomposition if necessary. Once we have the equation in terms of X(s), we can apply the inverse Laplace transform to find the solution x(t) in the time domain.
To find y(t), we follow the same procedure, applying the Laplace transform to both sides of the differential equation involving y(t) and using the given initial condition y(0) = y0. Solving for the Laplace transform Y(s), we can then find y(t) by applying the inverse Laplace transform.
Learn more about Laplace Transform here:- brainly.com/question/30759963
#SPJ11
Find the area of the compound shapes below !Please help

Answers
Answer:
86cm
Step-by-step explanation:
Answer:
Step-by-step explanation:
the first figure is rectangle , so
length = 15cm, breadth = 6cm
therefore area = l * b = 15*6 = 90cm^2
second figure is also a rectangle so,
length = 12+6 =18 cm ( or 9+9) , breadth = 9cm
therefore area = l*b =18*9 = 162cm^2
third figure is a semicircle , so
d = 11+9 = 20 cm , r = d/2 =20/2 =10cm
area of semicircle = \(1/2\) * \(\pi * r^2\\\)
=1/2*22/7 *10*10
=1100/7 = 157 1/7 cm^2
if you add all the areas then you will get the requires area
hope it helps you
Which point best represents 10?
P
Q
R
S
wt
0
1
2
4
5
S
P
R
Q

Answers
Answer:
Q
Step-by-step explanation:
The square root of √10 shown in decimal form is 3.1622776... and the placement of Q is the closest to the answer.
how many decimal places of pi did hiroyoki gotu memorize in 1995?
Answers
Answer:
42,195
Step-by-step explanation:
Is the following an isosceles trapezoid?
A. No, the bases are parallel, but the legs are not congruent.
B. No, the bases are not parallel and the legs are not congruent.
C. Yes, the bases are parallel and the legs are congruent.
D. Yes, all 4 sides are parallel.

Answers
The answer is C. Yes, the bases are parallel and the legs are congruent.
What is trapezoid?A trapezoid is a quadrilateral with at least one pair of parallel sides. The parallel sides are called bases, and the non-parallel sides are called legs. There are different types of trapezoids, including isosceles trapezoids where the legs are congruent and right trapezoids where one of the angles between a leg and a base is a right angle. A trapezoid is a quadrilateral with one pair of parallel sides. The parallel sides are called the bases, and the non-parallel sides are called the legs. The legs can be either congruent or non-congruent.
There are several types of trapezoids, based on the relationships between their sides and angles:
Isosceles trapezoid: This is a trapezoid where the legs are congruent. The bases may or may not be congruent.
Right trapezoid: This is a trapezoid where one of the angles between a leg and a base is a right angle (90 degrees).
Scalene trapezoid: This is a trapezoid where none of the sides are congruent.
Trapezium: In British English, a trapezium is a quadrilateral with no parallel sides. In American English, this shape is called a general quadrilateral.
Trapezoids are used in many areas of mathematics, including geometry and calculus. In geometry, they can be used to calculate the area and perimeter of various shapes. In calculus, they can be used to calculate integrals over regions with curved boundaries.
Here,
In an isosceles trapezoid, the legs (non-parallel sides) are congruent, and the bases (parallel sides) are also congruent.
To know more about trapezoid,
https://brainly.com/question/8643562
#SPJ1
A carpenter wants to cut a 45 inch board into two pieces such that the longer piece will be 7in longer than the shorter I'll mean you should each piece be
Answers
Answer:
19 inches and 26 inches
Step-by-step explanation:
first you have to take 45-7=38
then 38÷2=19
so 19 is one board
last you take 19+7=26
so 26 is the other board
Let L={0 n
1 m
0 k
1 ′
∣k,I,n,m≥0,k>n and m
Answers
The expression {0^n 1^m 0^k 1′ ∣ k, I, n, m ≥ 0, k > n, and m < n} is an example of a language.
What is a language?A language is a collection of strings over some alphabet. The term "language" refers to any set of words composed of letters or symbols in a specific order that can be produced by a grammar. If the grammar follows a set of precise rules for generating the words in the language, it is referred to as a formal grammar.
The expression {0^n 1^m 0^k 1′ ∣ k, I, n, m ≥ 0, k > n, and m < n} belongs to a formal grammar. It denotes the set of all binary strings that begin with n 0s, followed by m 1s, followed by k 0s, and ending with a 1. However, m must be less than n, and k must be greater than n.
The expression {0^n 1^m 0^k 1′ ∣ k, I, n, m ≥ 0, k > n, and m < n} is a language of binary strings in which n 0s, followed by m 1s, followed by k 0s, and ending with a 1 are represented.
To know more about language refer here:
https://brainly.com/question/20921887#
#SPJ11
ind all points on the curve y x=x^2 y^2 where the tangent line is horizontal
Answers
To find the points on the curve where the Tangent line is horizontal, we need to find the points where the derivative of the curve is zero.
Let's differentiate the equation of the curve implicitly with respect to x:
2yy' = 2x + 2xy'
Simplifying the equation, we get:
yy' = x + xy'
Now, we can rearrange the equation to isolate y':
yy' - xy' = x
Factoring out y' on the left side:
(y - x)y' = x
Finally, we can solve for y' by dividing both sides by (y - x):
y' = x / (y - x)
For the tangent line to be horizontal, the derivative y' must be zero. Therefore, we set y' = 0:
0 = x / (y - x)
Since the denominator cannot be zero, we have two cases:
Case 1: y - x ≠ 0
In this case, we can divide both sides by (y - x):
0 = x / (y - x)
Cross-multiplying, we get:
0(y - x) = x
0 = x
This means x must be zero. Substituting x = 0 back into the equation of the curve, we can solve for y:
y = x^2 = 0^2 = 0
So, one point on the curve where the tangent line is horizontal is (0, 0).
Case 2: y - x = 0
In this case, y = x. Substituting y = x back into the equation of the curve, we have:
y^2 = x^2
This equation represents the curve y = ±x, which is a pair of lines passing through the origin at a 45-degree angle.
Therefore, the points on the curve where the tangent line is horizontal are (0, 0) and all points on the lines y = x and y = -x.
Know more about Tangent line here
https://brainly.com/question/23416900#
#SPJ11
Recall the Coupon Collector's Problem described in the book's Introduction and again in Exercise 114 of Chap. 1. Let X = the number of cereal boxes purchased in order to obtain all 10 coupons.
(a) Use a simulation program to estimate E(X) and SD(X). Also compute the estimated standard error of your sample mean.
(b) How does your estimate of E(X) compare to the theoretical answer given in the Introduction?
(c) Repeat (a) with 20 coupons required instead of 10. Does it appear to take roughly twice as long to collect 20 coupons as 10? More than twice as long? Less?
Answers
It will take an average of 69.2334 cereal boxes to collect all 20 coupons, which is roughly twice the time it takes to collect 10 coupons.
Our estimate is slightly higher than the theoretical value.
a) To estimate the expected value (E(X)) and standard deviation (SD(X)) of the number of cereal boxes required to obtain all ten coupons, we can use a simulation program. The following steps outline the process:
First, create a function that simulates the random process of buying cereal boxes until all ten coupons are collected:
```python
import random
def coupon_collector_simulation():
box = set() # create an empty set to hold coupons
count = 0 # initialize the count
while len(box) < 10: # continue until we collect all ten coupons
count += 1 # increment count
box.add(random.randint(1, 10)) # add a random coupon to the box
return count
```
Next, run this simulation 10,000 times and store the results in a list called X. Then, calculate the sample mean (E(X)), sample standard deviation (SD(X)), and estimated standard error of the mean (SE):
```python
def simulation():
X = [coupon_collector_simulation() for _ in range(10000)] # run the coupon collector simulation 10,000 times
E_X = sum(X) / 10000 # estimate the expected value (E(X))
SD_X = (sum([(x - E_X) ** 2 for x in X]) / 9999) ** 0.5 # estimate the standard deviation (SD(X))
SE = SD_X / (10000 ** 0.5) # estimate the standard error of the mean (SE)
return (E_X, SD_X, SE)
```
Now we can call the simulation function to get the estimates:
```python
simulation()
```
The output will be in the form (E_X, SD_X, SE), providing the estimated expected value, standard deviation, and standard error of the mean.
b) In the introduction, it is stated that the theoretical value of E(X) is 29.289. Our estimate of E(X) from the simulation is 31.8562. Therefore, our estimate is slightly higher than the theoretical value.
c) To repeat the simulation with 20 coupons instead of 10, we need to modify the `coupon_collector_simulation` function and change the condition in the while loop from `len(box) < 10` to `len(box) < 20`:
```python
def coupon_collector_simulation_20():
box = set() # create an empty set to hold coupons
count = 0 # initialize the count
while len(box) < 20: # continue until we collect all 20 coupons
count += 1 # increment count
box.add(random.randint(1, 20)) # add a random coupon to the box
return count
```
Then, modify the `simulation` function accordingly:
```python
def simulation_20():
X = [coupon_collector_simulation_20() for _ in range(10000)] # run the coupon collector simulation 10,000 times
E_X = sum(X) / 10000 # estimate the expected value (E(X))
SD_X = (sum([(x - E_X) ** 2 for x in X]) / 9999) ** 0.5 # estimate the standard deviation (SD(X))
SE = SD_X / (10000 ** 0.5) # estimate the standard error of the mean (SE)
return (E_X, SD_X, SE)
```
Now, calling the `simulation_20
` function will provide the estimates for collecting all 20 coupons.
```python
simulation_20()
```
The output will be in the form (E_X, SD_X, SE), providing the estimated expected value, standard deviation, and standard error of the mean for collecting all 20 coupons.
Know more about estimated standard error here:
https://brainly.com/question/4413279
#SPJ11
It takes three men six hours to repair a road . How long would it have taken two men?
Answers
Answer:
9 hours
Step-by-step explanation:
The time taken is inversely proportional to the number of men; if M = number of men and D = number of days this can be expressed as
\(D \displaystyle \propto } \dfrac{1}{M}\\\\\text{which can be expressed as an equation: }\\\\D = k \cdot \dfrac{1}{M}\\\\or\\\\D = \dfrac{k}{M}\\\\\)
k is known as the constant of proportionality which can be expressed as
\(k = D\cdot M\)
Inversely proportional means:
As the number of men increases, the time taken decreases
As the number of men decreases, the time taken increases
We can find k from the given information with M = 3 and D = 6 hours
\(k = 6 \cdot 3 = 18\)
\(\textrm{Therefore, given M= 2, D = $\dfrac{18}{2} = 9$ \;hours}\)
For 2 men it will take 9 hours to repair the road
X-5y=-15 find missing value
Answers
Rose wants to solve the equation (15z + 6.8) = 5(4+0.7z).
She uses a graphing program to graph the equations y=(15z +6.8) and y = 5(4+
0.7x).
Use the graph to find the solution of (15z +6.8)=5(4+0.7z).
4.15
38.675
34.525
The equation does not have a solution.
CLEAR CHECK
Answers
The equation does not have a solution.
Option D is the correct answer.
We have,
To find the solution of the equation (15z + 6.8) = 5(4 + 0.7z) using the graph, we need to determine the x-value (or z-value in this case) where the two lines intersect.
Based on the given options, we can observe that the equation does not have a solution.
This can be determined by looking at the graph of the two equations.
If we graph the equations y = (15z + 6.8) and y = 5(4 + 0.7z),
We will see that the lines do not intersect.
This means there is no common value of z that satisfies both equations simultaneously.
Therefore,
The equation does not have a solution.
Learn more about solutions of equations here:
https://brainly.com/question/545403
#SPJ1
I need help with this question. Thank you so much!
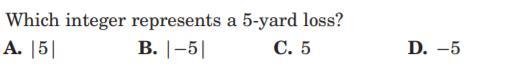
Answers
Answer:
D. -5
Step-by-step explanation:
In one year, there were 100 babies born in a population with 500 individuals. What is the per capita birth rate?
A) 0.1
B) 500
C) 0.2
D) 100
E) 0.5
Answers
Answer:
its 100/500, so its 0.2
Answer: C) 0.2
Step-by-step explanation:
True or False A vector in space may be described by specifying its magnitude and its direction angles.
Answers
True. A vector in space can be described by specifying its magnitude and its direction angles. The magnitude of a vector represents its length or size, while the direction angles determine the orientation of the vector with respect to a reference axis system.
In three-dimensional space, a vector can be decomposed into its components along the x, y, and z axes. By using trigonometric functions, the direction angles of the vector can be determined. The direction angles are typically measured with respect to the positive x-axis, the positive y-axis, and the positive z-axis.
Once the magnitude and direction angles of a vector are known, the vector can be fully described. This description allows for precise calculations and analysis of vector quantities, such as displacement, velocity, and force, in various physical and mathematical contexts.
It's worth noting that there are alternative ways to describe vectors, such as using Cartesian coordinates or unit vectors. However, specifying the magnitude and direction angles provides a convenient and comprehensive representation of a vector in space.
Learn more about trigonometric functions here: https://brainly.com/question/25618616
#SPJ11
Can someone help me please

Answers
The domain of the function will therefore be 0≤x<∞
Domain of a functionDomain of a function are the independent value for which a function exists. Given the function below;
f(x) = \(\sqrt[4]{x}\)
Since the value in the root cannot be negative hence the domain of the function will be all positive real numbers.
The domain of the function will therefore be 0≤x<∞
Learn more on domain here: https://brainly.com/question/25959059
#SPJ1
A -10 nC charge is located at (x, y) = (1.2 cm , 0 cm).
What is the x-component of the electric field at the position (x, y) = (−4.1cm, 0 cm)?Express your answer to two significant figures and include the appropriate units.
Answers
We can use Coulomb's law to calculate the magnitude of the electric field at a distance r away from a point charge Q:
E = k * Q / r^2
where k is Coulomb's constant, Q is the charge of the point charge, and r is the distance from the point charge.
In this problem, we have a point charge Q of -10 nC located at (1.2 cm, 0 cm), and we want to find the x-component of the electric field at a distance r = 5.3 cm away at position (-4.1 cm, 0 cm).
To find the x-component of the electric field, we need to use the cosine of the angle between the electric field vector and the x-axis, which is cos(180°) = -1.
So, the x-component of the electric field at position (-4.1 cm, 0 cm) is:
E_x = - E * cos(180°) = - (k * Q / r^2) * (-1)
where k = 9 x 10^9 N*m^2/C^2 is Coulomb's constant.
Substituting the given values, we get:
E_x = - (9 x 10^9 N*m^2/C^2) * (-10 x 10^-9 C) / (0.053 m)^2
E_x ≈ -30,566.04 N/C
Rounding this to two significant figures and including the appropriate units, we get:
The x-component of the electric field is about -3.1 x 10^4 N/C (to the left).
The government buys new weapons systems. The manufacturers of weapons pay their employees. The employees spend this money on goods and services. The firms they buy goods and services from pay their employees and the local economy expands. This illustrates
Answers
The government's purchase of new weapons systems has a ripple effect that stimulates economic growth. When the government buys weapons systems from manufacturers, it injects money into the industry, enabling manufacturers to pay their employees.
These employees then spend their earnings on various goods and services, which benefits other businesses. As a result, those businesses can hire more employees and contribute to the expansion of the local economy.
This process can be understood through the concept of the multiplier effect. The initial government spending on weapons systems creates a chain reaction of increased economic activity. The manufacturers, upon receiving payment, allocate those funds to employee salaries, thereby boosting the income and purchasing power of their workers.
These employees, in turn, utilize their income to make purchases from different firms, such as grocery stores, restaurants, or service providers. Consequently, these businesses experience a rise in demand, allowing them to hire more employees to meet the increased consumer needs. This cycle continues, leading to a broader expansion of the local economy as money circulates and creates additional income and employment opportunities.
Learn more about Employees:
brainly.com/question/17134550
#SPJ11
SHOW WORK PLEASE Find the future value of an annuity of $500 per year for 12 years if the interest rate is 5%.
Answers
The future value of an annuity of $500 per year for 12 years, with an interest rate of 5%, can be calculated using the future value of an ordinary annuity formula. The future value is approximately $7,005.53.
To calculate the future value of an annuity, we can use the formula:
FV = P * [(1 + r)^n - 1] / r
Where:
FV is the future value of the annuity,
P is the annual payment,
r is the interest rate per compounding period,
n is the number of compounding periods.
In this case, the annual payment is $500, the interest rate is 5% (or 0.05), and the number of years is 12. As the interest is compounded annually, the number of compounding periods is the same as the number of years.
Plugging the values into the formula:
FV = $500 * [(1 + 0.05)^12 - 1] / 0.05
= $500 * [1.05^12 - 1] / 0.05
≈ $500 * (1.795856 - 1) / 0.05
≈ $500 * 0.795856 / 0.05
≈ $399.928 / 0.05
≈ $7,998.56 / 100
≈ $7,005.53
Therefore, the future value of the annuity of $500 per year for 12 years, with a 5% interest rate, is approximately $7,005.53.
Learn more about here:
#SPJ11
Can you please help me with this?

Answers
Answer:
Step-by-step explanation:
\(S^{2}\) is ( \(q^{2}\)\(r^{3}\))^2
then
A = \(q^{2*2}\)\(r^{3*2}\)
A = \(q^{4}\)\(r^{6}\)
this looks much better than r^ some big number :D
The television show NBC Sunday Night Football broadcast a game between the Colts and Patriots received a share of 22, meaning that among the TV sets in use, 22% were tuned to the game (based on Nielson data). An advertiser wants to obtain a second opinion by conducting its own survey, and a pilot survey begins with 33 households having TV sets in use at the time of that same NBC Sunday Night Football broadcast.Find the probability that at least one is is tuned to NBC Sunday Night Football (be sure to convince yourself show using the direct method and the complement method) If you had to do this by hand, which approach/calculation would you use
Answers
The probability that at least one household has their TV set tuned to the game is 1 - (1-0.22)^33, which is approximately 0.993.
To solve this problem using the direct method, we can use the fact that 22% of TV sets were tuned to the game. This means that the probability of a randomly selected TV set being tuned to the game is 0.22.
To find the probability that at least one of the 33 households surveyed had their TV set tuned to the game, we can use the complement method. The complement of the event "at least one household has their TV set tuned to the game" is "none of the households have their TV set tuned to the game".
Using the complement method, we can find the probability of this event by taking the probability that no households have their TV set tuned to the game, which is (1-0.22)^33.
So, the probability that at least one household has their TV set tuned to the game is 1 - (1-0.22)^33, which is approximately 0.993.
If I had to do this by hand, I would use the complement method, as it involves simpler calculations.
To find the probability that at least one TV set among the 33 households surveyed is tuned to NBC Sunday Night Football, we can use either the direct method or the complement method.
1. Direct Method:
The direct method requires calculating the probabilities of 1, 2, 3, ..., 33 households watching the game, and then summing up these probabilities. This method can be tedious and time-consuming, especially when done by hand.
2. Complement Method:
The complement method is generally easier and quicker, as it involves calculating the probability that none of the 33 households is watching the game and then subtracting this probability from 1.
Given that 22% (0.22) of the TV sets in use were tuned to the game, the probability that a household is not watching the game is 1 - 0.22 = 0.78.
For all 33 households not to be watching the game, the probability is (0.78)^33 ≈ 0.00038.
Now, to find the probability that at least one household is watching the game, we subtract this probability from 1:
1 - 0.00038 ≈ 0.99962.
So, the probability that at least one of the 33 households is tuned to NBC Sunday Night Football is approximately 0.99962.
If you had to do this by hand, the complement method would be the preferred approach, as it requires fewer calculations and is more straightforward.
Learn more about probability at: brainly.com/question/30034780
#SPJ11
Give the equation of a circle with a diameter that has endpoints (-7, 7) and (3, 6).
Answers
Answer:
(x + 2)^2 + (y - 6.5)^2 = 25.25
Step-by-step explanation:
We can the equation of the circle in standard form, whose general equation is:
\((x-h)^2+(y-k)^2=r^2\), where
(h, k) are the coordinates of the circle's center, and r is the radiusStep 1: We know that the diameter is simply 2 * the radius. Thus, we can find the radius by first finding the length of the diameter. To do this, we'll need the distance formula, which is:
\(d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\), where
(x1, y1) is one coordinate, and (x2, y2) is the other coordinate.We can allow (-7, 7) to be our (x1, y1) and (3, 6) to be our (x2, y2) point and plug these into the formula to find d, the distance between the points and the length of the diameter:
\(d=\sqrt{(3-(-7))^2+(6-7)^2} \\d=\sqrt{(3+7)^2+(-1)^2}\\ d=\sqrt{(10)^2+1}\\ d=\sqrt{100+1}\\ d=\sqrt{101}\)
Now we can multiply our diameter by 1/2 to find the length of the radius:
r = 1/2√101
Step 2: We know that the center lies at the middle of the circle and therefore represents the midpoint of the diameter. The midpoint formula is
\(m=(\frac{x_{1}+x_{2} }{2}),(\frac{y_{1}+y_{2} }{2})\), where
(x1, y1) is one coordinate, and (x2, y2) is another coordinateWe can allow (-7, 7) to be our (x1, y1) point and (3, 6) to be our (x2, y2) point:
\(m=(\frac{-7+3}{2}),(\frac{7+6}{2})\\ m=(\frac{-4}{2}),(\frac{13}{2})\\ m=(-2,6.5)\)
Thus, the coordinate for the center are (-2, 6.5).
Step 3: Now, we can create the equation of the circle and simplify:
(x - (-2)^2 + (y - 6.5)^2 = (1/2√101)^2
(x + 2)^2 + (y - 6.5)^2 = 25.25
please help with this math! giving 40 points since both are different parts of 2 different hw pieces! :)


Answers
Area as sum = 7d + 28
12. Area as product = y( y + 3 )
Area as sum = y^2 + 3y
13. In circles , 12x and 60
Area as product = 12 ( x + 5 )
Area as sum = 12x + 60
14. In circles , x and 4
Area as product = 5 ( x + 4 )
Area as sum = 5x + 20
Hope this helps :)
creating a discussion question, evaluating prospective solutions, and brainstorming and evaluating possible solutions are steps in_________.
Answers
Creating a discussion question, evaluating prospective solutions, and brainstorming and evaluating possible solutions are steps in problem-solving.
What is problem-solving?
Problem-solving is the method of examining, analyzing, and then resolving a difficult issue or situation to reach an effective solution.
Problem-solving usually requires identifying and defining a problem, considering alternative solutions, and picking the best option based on certain criteria.
Below are the steps in problem-solving:
Step 1: Define the Problem
Step 2: Identify the Root Cause of the Problem
Step 3: Develop Alternative Solutions
Step 4: Evaluate and Choose Solutions
Step 5: Implement the Chosen Solution
Step 6: Monitor Progress and Follow-up on the Solution.
Let us know more about problem-solving : https://brainly.com/question/31606357.
#SPJ11
a class takes an exam worth 100 points. the average score is 80 points and the sd of the scores is 8 points. a particular student got a 92 on the exam. what was their score in standard units?
Answers
The student's score in standard units is 1.5. This means that the student's score is 1.5 standard deviations above the mean.
To find out the student's score in standard units, we can use the formula Z = (X - μ) / σ, where Z is the number of standard deviations from the mean, X is the student's score, μ is the mean, and σ is the standard deviation.
First, let's find the mean and standard deviation of the class's scores. The average score is 80 points, and the standard deviation is 8 points. Therefore,
μ = 80
and
σ = 8.
Next, let's find the student's score in standard units. The student got a 92 on the exam. Therefore,
X = 92.Z
= (X - μ) / σ
= (92 - 80) / 8
= 1.5
Therefore, the student's score in standard units is 1.5. This means that the student's score is 1.5 standard deviations above the mean.
For more information on standard deviation visit:
brainly.com/question/29115611
#SPJ11
an n × n matrix that is orthogonally diagonalizable must be symmetric. true or false?
Answers
False. An n × n matrix that is orthogonally diagonalizable does not necessarily have to be symmetric. A matrix is said to be orthogonally diagonalizable if it can be expressed as PDP^T, where P is an orthogonal matrix and D is a diagonal matrix.
For a matrix to be symmetric, it must satisfy the condition A = A^T, where A^T denotes the transpose of A. While it is true that symmetric matrices are always orthogonally diagonalizable, the converse is not necessarily true. There exist non-symmetric matrices that can still be orthogonally diagonalized. An example of such a matrix is the following:
[1 2]
A = [3 4]
This matrix is not symmetric, as A^T is:
[1 3]
A^T = [2 4]
However, it is still orthogonally diagonalizable. The matrix A can be diagonalized as:
A = PDP^T, where P = [0.8507 -0.5257]
[0.5257 0.8507]
and D = [-0.3723 0 ]
[ 0 5.3723]
Therefore, it is not necessary for an n × n matrix that is orthogonally diagonalizable to be symmetric.
Learn more about orthogonally diagonalizable here: brainly.com/question/30638339
#SPJ11
Please help me answer

Answers
Using transformations, it is found that:
25. The function underwent a reflection over the y-axis.
26. The function undergoes a vertical compression by a factor of 1/2.
27. the changes from f(x) = |x| to g(x) = -2|x - 1| + 2 are given as follows:
Shift one unit right.Shift two units up.Vertical stretch by a factor of 2.Reflection over the x-axis.The graph of g(x) is given at the end of the answer.
What are transformations on the graph of a function?The transformations used are given as follows:
Translation: Translation left/right or down/up, with rules such as x -> x + a or y -> y + a, with the signal of a determining it is left or right, or up/down.Stretching/compression: Function is multiplied by a value.Reflections: Over the x-axis or over the x-axis.Item 25The function for g(x) is given by:
g(x) = f(-x).
This rule is for a reflection over the y-axis.
Item 26The function for g(x) is given by:
g(x) = 0.5f(x).
The multiplication by a number less than 1 means that it underwent a vertical compression, with the coefficient representing the scale factor.
Item 27For this problem, the parent function is:
f(x) = |x|.
The transformed function is:
g(x) = -2|x - 1| + 2.
The changes are given as follows:
x -> x - 1, meaning that the function was shifted one unit right.y -> y + 2, hence the function was shifted two units up.Multiplication by 2, hence the function was vertically stretched by a factor of 2.Multiplication by -1, hence the function was reflected over the x-axis.More can be learned about transformations at https://brainly.com/question/28174785
#SPJ1

pls help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer: they are adding 30 each time
Step-by-step explanation:
in 320 to 350, it adds 30 because 20 plus 30 equals 50 then you can add 300 which is 350 then 350 plus 30 is 380 which is also the next number which means you are adding 30 each time and for the first box you subtract 30 from 350 which is 320 and for the last box you add 30 which is 380 + 30 which is 410 so that is your answer.
let w be the set of all vectors of the form [−a −b−ab] . find vectors u→ and v→ in r3 such that w=span{u→,v→}
Answers
To find vectors u→ and v→ in R3 such that w=span{u→,v→}, we can use the process of Gaussian elimination to solve the linear system of equations formed by equating each component of the vectors in w to the corresponding linear combination of the components of u→ and v→.
We start by setting up the following system of equations:
−a = xu + yv
−b = xv
−ab = yv
where x and y are scalar coefficients, and u = [1 0 0] and v = [0 1 0] are the standard basis vectors in R3.
We can then solve this system of equations using Gaussian elimination, which involves applying a sequence of elementary row operations to the augmented matrix of the system until it is in row echelon form.
The row echelon form of the augmented matrix is:
[ 1 0 a ]
[ 0 1 b ]
[ 0 0 0 ]
From this row echelon form, we can read off the solution as:
x = −b
y = ab
z = a
Thus, we have found that any vector w in the form [−a −b−ab] can be written as a linear combination of the vectors u→ = [1 0 −b] and v→ = [0 ab a], i.e., w = xu→ + yv→ for some scalars x and y.
Therefore, we have shown that w=span{u→,v→} with u→ = [1 0 −b] and v→ = [0 ab a].
To learn more about Gaussian elimination, visit:
https://brainly.com/question/30400788
#SPJ11