25 points and brainiest
2. If you get paid hourly, making $1000 a week, but work 65 hours per week how much are you making hourly?
3. If you get paid hourly, making $25.00 an hour, but work 20 hours’ overtime per week, what is your weekly pay?
4. If you get paid hourly at a job making $25.00 an hour, but have to call in sick for one day of work, how much would you get paid at the end of the week assuming you normally work 40 hours and get no sick leave.
Answers
3. Assuming that you get time and a half for OT.
$25 x 45hrs + 1.5(20hrs x $25)
= $1125 + $750
=$1875
4. You lose 8 hrs pay. So you only work 32 hrs.
32hrs x $25 = $800
Related Questions
Find the 12th term of the following geometric sequence. 2, 8, 32, 128
Answers
Step-by-step explanation:
So 2 * 4 = 8
8 * 4 = 32
32 * 4 = 128
128 * 4 = 512
512*4=2048
2048*4=8192
8192*4=32768
32768*4=131072
131072*4=524288
524288*4=2097152
2097152*4=8388608
8388608*4=33554432 and that would probably be your final answer
Find a solution of the initial-value problem.
14. y' = 6e^2x−y, y(0) = 0
16. dy/dx= e^x−y/1 + e^x, y(1) = 0
18. y' = x√1 − y^2/1− x^2, y(0) = 0
the square root on problem 18 is over the rest of the equation....square root over 1-y^2/1-x^2
Answers
The y:y' = x*sqrt((1 - y^2)/(1 - x^2))dy/sqrt(1 - y^2) = x dx/sqrt(1 - x^2)arcsin y = -arcsec x + KSince C = 0, we have:y(x) = sin(-arcsec x)
14. Solution of the initial-value problem:y' = 6e^(2x)-y, y(0) = 0Let y' = f(y, x), and then let's use the initial condition to find the arbitrary constant:C = y(0) = 0Now let's solve for y:(dy)/(dx) + y = 6e^(2x) = (f(y, x) + y = 6e^(2x))Using the integrating factor µ = e^x, we can solve the problem using the formula:y(x) = [e^(∫µ(x)dx) * C] + [e^(∫µ(x)dx) * ∫µ(x) * f(x) dx]y(x) = [e^(x) * C] + [e^(x) * ∫6e^(2x) * e^x dx]y(x) = [e^(x) * C] + [6/3 * e^(3x) + K]Since C = 0, we have:y(x) = [6/3 * e^(3x) + K]y(x) = 2e^(3x) + K16. Solution of the initial-value problem:dy/dx = (e^x-y)/(1+e^x), y(1) = 0Let y' = f(y, x), and then let's use the initial condition to find the arbitrary constant:C = y(1) = 0Now let's solve for y:dy/dx + y/(1 + e^x) = e^x/(1 + e^x)Using the integrating factor µ = e^(x)/(1 + e^x), we can solve the problem using the formula:y(x) = [e^(∫µ(x)dx) * C] + [e^(∫µ(x)dx) * ∫µ(x) * f(x) dx]y(x) = [e^(∫e^(x)/(1 + e^x) dx) * C] + [e^(∫e^(x)/(1 + e^x) dx) * ∫(e^x)/(1 + e^x) * e^x dx]y(x) = [e^(ln(1 + e^x)) * C] + [e^(ln(1 + e^x)) * ∫(e^x)/(1 + e^x) * e^x dx]y(x) = [1 + e^x * C] + [(1 + e^x) * ∫(e^x)/(1 + e^x) dx]y(x) = [1 + e^x * C] + [(1 + e^x) * ln|1 + e^x| - e^x + K]Since C = 0, we have:y(x) = (1 + e^x) * ln|1 + e^x| - e^x + K18. Solution of the initial-value problem:y' = x*sqrt((1 - y^2)/(1 - x^2)), y(0) = 0Let y' = f(y, x), and then let's use the initial condition to find the arbitrary constant:C = y(0) = 0Now let's solve for y:y' = x*sqrt((1 - y^2)/(1 - x^2))dy/sqrt(1 - y^2) = x dx/sqrt(1 - x^2)arcsin y = -arcsec x + KSince C = 0, we have:y(x) = sin(-arcsec x)
Learn more about Sqrt
brainly.com/question/30086102
#SPJ11
what is 4 1/5 divided by 2/3
Answers
Answer:
6 3/10
Step-by-step explanation:
They are planting each tree 12 feet apart. how many trees can they plant on 2 miles of streets
Answers
Answer: 880 Trees
Step-by-step explanation:
To determine the number of trees that can be planted on 2 miles of streets, we need to convert the distance from miles to feet and then divide it by the spacing between each tree.
1 mile is equal to 5,280 feet. Therefore, 2 miles would be 2 * 5,280 = 10,560 feet.
If each tree is planted 12 feet apart, we can calculate the number of trees by dividing the total distance by the spacing between each tree:
Number of trees = Total distance / Spacing between each tree
Number of trees = 10,560 feet / 12 feet
Number of trees = 880
Therefore, they can plant 880 trees on 2 miles of streets, assuming each tree is planted 12 feet apart.
A computer costs $1300 new and then depreciates $25 each month.
Find the value, V, of the computer after t months.
Answers
The value of a computer depreciates by $25 each month. Given that the computer initially costs $1300, we need to determine the value of the computer after t months.
To find the value of the computer after t months, we subtract the total depreciation from the initial cost. The total depreciation can be calculated by multiplying the depreciation per month ($25) by the number of months (t). Therefore, the value V of the computer after t months is given by V = $1300 - $25t.
This equation represents a linear relationship between the value of the computer and the number of months. Each month, the value decreases by $25, resulting in a straight line with a negative slope. The value of the computer decreases linearly over time as the depreciation accumulates. By substituting the appropriate value of t into the equation, we can find the specific value of the computer after a certain number of months.
To learn more about depreciates: -brainly.com/question/15085226#SPJ11
Let {X t
} an ARIMA process (2,1,0) given by: (1−0.8B+0.25B 2
)∇X t
=Z t
{Z t
}∼WN(0,1) Determine the forecast function. g(h)=P n
X n+h
∀h>0
Answers
Therefore, the forecast function g(h) is given by: g(h) = Xn + 0.8(Xn+1 - Xn) - 0.25(Xn+2 - Xn+1) for h > 0.
To determine the forecast function g(h) for an ARIMA(2,1,0) process, we need to find the values of Xn+h for each h > 0.
The ARIMA(2,1,0) model can be represented as (1 - 0.8B + 0.25B^2)∇Xt = Zt, where ∇Xt represents the differenced series and Zt is white noise with mean 0 and variance 1.
To forecast the future values, we need to solve the difference equation for ∇Xn+h. Let's denote the difference operator as Δ = (1 - B) and rewrite the model as:
Δ(1 - 0.8B + 0.25B^2)Xt = Zt
Expanding the expression, we have:
Xn+h - Xn - 0.8(Xn+1 - Xn) + 0.25(Xn+2 - Xn+1) = Zn+h
Rearranging the equation, we get:
Xn+h = Xn + 0.8(Xn+1 - Xn) - 0.25(Xn+2 - Xn+1) + Zn+h
Therefore, the forecast function g(h) is given by:
g(h) = Xn + 0.8(Xn+1 - Xn) - 0.25(Xn+2 - Xn+1) for h > 0.
Learn more about forecast here:
https://brainly.com/question/21445581
#SPJ11
MAX is equiangular. m
Answers
Answer:
x = 8
Step-by-step explanation:
If equiangular, than all angles are equal
Thus, we have that;
7x + 4 = 12x-36
12x-7x = 36 + 4
5x = 40
x = 40/5
x= 8
Find the value of X below
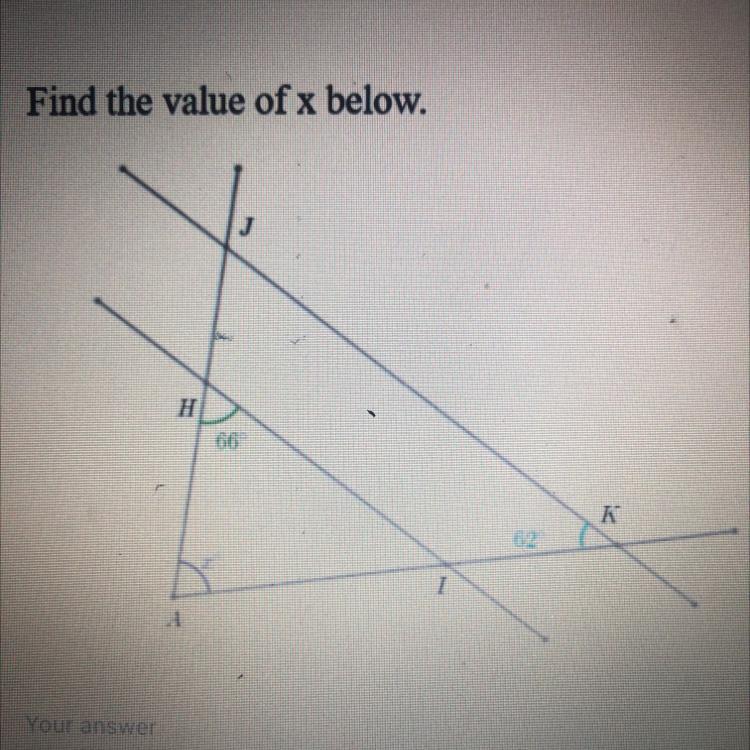
Answers
52° is your answer
Hope it helps
POSSIBLE POINTS 162 + 122Which equation written below in vertex form is equivalent to the equation y = 22Oy= (x – 3)Oy= (2-6)² + 12Oy= (x+3)+ 3Oy= (2 – 3)2 +3

Answers
Given:
\(y=x^2-6x+12\)\(y=x^2-6x+3^2-3^2+12\)\(y=(x-3)^2-9+12\)\(y=(x-3)^2+3\)prtion D is the correct answer.
vincent, a quality control manager at an outdoor apparel manufacturing company, studies and monitors quality using r-charts. he discovers a quality problem with the construction of zippers. vincent proposes that 25 samples of eight observations each be collected on a daily basis. he plans to prepare an r-chart to monitor the variation in the size of the zippers. the data collected shows that the mean length of the zippers is 15 inches and the average range is 0.5 inches. if d3 for the r-chart is 0.136, the lower control limit (lclr) for the r-chart will be: a. less than or equal to 1. b. more than 1 but less than or equal to 2. c. more than 2 but less than or equal to 3. d. more than 4.
Answers
lowest control limit (LCL^{R} ) for R chart is equal to 0.068 inches
and 0.068 is less than 1 .So the correct answer is( A) less than or equal to 1 .
What is lowest control limit?
The lower control limit on a control chart is a line that runs parallel to the centerline and denotes the value below which any particular data point would be deemed to be outside statistical control due to special cause variation.
Total sample = 25
sample size = 8 observation
mean length of the zippers = 15 inches
average range = 0.5 inches
D3 for R chart = 0.136
Formula = \(LCL^{R}\) = D₃ R
Put the values
R = 0.5 Inches
D₃ = 0.136
LCL^{R} = D₃ R
= 0.136 * 0.5 = 0.068 inches
Thus lowest control limit (LCL^{R} ) for R chart is equal to 0.068 inches
and 0.068 is less than 1 .
Learn more about lowest control limit
brainly.com/question/15298022
#SPJ4
26=6(5-a)
What is a
Answers
Answer:
2/3
Step-by-step explanation:
Simplify
\(26=6\cdot \left(5-a\right)\\26=6\cdot 5+6\cdot -a\\26=30+6\cdot -a\\26=30+\left(6\cdot -1\right)a\\26=30-6a\\30-6a=26\)
Group constants
\(30-6a=26\\30-6a-30=26-30\\-6a+30-30=26-30\\-6a=26-30\\-6a=-4\\\)
Isolate the term, a
\(-6a=-4\\\frac{-6a}{-6}=\frac{-4}{-6}\\\frac{6a}{6}=\frac{-4}{-6}\\a=\frac{-4}{-6}\\\\\frac{-a}{-b} = \frac{a}{b}\\\\a=\frac{4}{6}\\a=\frac{2\cdot 2}{3\cdot 2}\\a=\frac{2}{3}\)
ten people were asked if they had a brother or sister, this Venn diagram shows the results. A person was randomly chosen from those shown on the Venn diagram.
let event A = person has a sister
let event B = person has a brother
what does P(B|A) = 0.50 mean in terms of the Venn diagram?
the photo below shows the Venn diagram as well as the possible answers

Answers
The Venn diagram shows that P(B|A) = 0.50 means that of the ten people surveyed, five of these have only a brother or only a sister. Option C.
What is probability?
Probability is a measure of the likelihood that a particular event will occur. It is a number between 0 and 1, with 0 indicating that an event is impossible and 1 indicating that an event is certain.
Events with a probability between 0 and 1 are known as possible events. The probability of an event is often represented as a decimal or fraction, and can also be expressed as a percentage.
Learn more about probability:https://brainly.com/question/30034780
#SPJ1
Megan is in charge of creating a five-digit code to lock and unlock a secure room. She can use any digit from 0 through 9, and she can use each digit as many times as she wants. She knows she wants to start the code with a 7.
How many possible codes that start with 7 could Megan create?
10,000 codes
70,000 codes
100,000 codes
700,000 codes
Answers
Answer:
The Answer Is 10,000 Codes
Proof :

Answer:
10,000
Step-by-step explanation:
Took k-12 quiz
find the 3x3 matrix that corresponds to the composite transformation of a scaling by 2, a rotation of 90o about the origin
Answers
The 3x3 matrix after composite transformation of scaling by 2, a rotation of 90° about origin is \(\left[\begin{array}{ccc}2c&2d&2i\\2b&2e&2h\\2a&2d&2g\end{array}\right]\).
Let A=\(\left[\begin{array}{ccc}a&b&c\\d&e&f\\g&h&i\end{array}\right]\) be a 3x3 matrix
scaling the matrix A by 2 then the result will be
\(2A=2\left[\begin{array}{ccc}a&b&c\\d&e&f\\g&h&i\end{array}\right]\\\\=\left[\begin{array}{ccc}2a&2b&2c\\2d&2e&2f\\2g&2h&2i\end{array}\right]\)
now, rotating the resultant matrix by 90° in counterclockwise direction about the origin, we get
\(=\left[\begin{array}{ccc}2c&2d&2i\\2b&2e&2h\\2a&2d&2g\end{array}\right]\)
Thus, a 3x3 matrix after composite transformation of scaling by 2, a rotation of 90° about origin is \(\left[\begin{array}{ccc}2c&2d&2i\\2b&2e&2h\\2a&2d&2g\end{array}\right]\)
To learn more about transformation of matrices refer here
https://brainly.com/question/16956653
#SPJ4
What is the equation, in point-slope form, of the line
that is perpendicular to the given line and passes
through the point (-4, -3)?
A: y + 3 = -4(x + 4)
B: y + 3 = -1/4(x+4)
C: y + 3 = 1/4(x + 4)
D: y + 3 = 4(x + 4)

Answers
Answer:
C: y + 3 = 1/4(x + 4)
Step-by-step explanation:
Perpendicular to a given line means opposite inverse of the slope...
Equation of line is: y = -4x - 3
slope in above equation is -4, perpendicular would be 1/4
Perpendicular equation of a line through P(-4, -3):
y = mx + b
-3 = 1/4(-4) + b
-3 = -1 + b
b = -2
Use perpendicular slope and the b from above to form the perpendicular equation of line:
y = 1/4x - 2
Check:
(-3) = 1/4(-4) - 2
-3 = -1 - 2
-3 = -3
What is the sum?
X
3
2
+
X+3 x+3 x+3
O
+
colch
53
X+5
X+3
X+5
3x+27
6x
X+3

Answers
The outcome or result of adding two or more integers is known as the SUM.
What is a sum?The outcome of adding numbers or quantities mathematically is a summation, often known as a sum. A summation always has an even number of terms in it. There may be just two terms, or there may be 100, 1000, or even a million. Some summations include an infinite number of terms.
the sum of two or more numbers, magnitudes, quantities, or specifics as determined by or as though decided by the addition process in mathematics.
The outcome of adding two or more numbers, objects, or things is referred to in mathematics as the sum.
The result or solution we obtain from adding two or more integers is known as the SUM. Addends are the figures that are combined.
\(Simplify $\frac{x}{x+3}+\frac{3}{x+3}+\frac{2}{x+3}: \frac{x+5}{x+3}$Steps$$\frac{x}{x+3}+\frac{3}{x+3}+\frac{2}{x+3}$$Apply the fraction rule: $\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$$$=\frac{x+3+2}{x+3}$$Add the numbers: $3+2=5$$$=\frac{x+5}{x+3}$$\)
Therefore, the correct answer is option b) \($=\frac{x+5}{x+3}$\)
To learn more about sum refer to:
https://brainly.com/question/25734188
#SPJ1
Please help it’s due today

Answers
Answer:
x = 2/3
Step-by-step explanation:
cross multiply
-9(x-4) = 10(3x+1)
and then solve the equation
-9x + 36 = 30x + 10
36 = 39x + 10
26 = 39x
x = 2/3
-9(x-4) = 10(3x + 1)
-9x + 36 = 30x + 10
-9x = 30x - 26
-39x = -26
X = -26/-39 = 2/3
The solution is x = 2/3
Please help me I need help puhleass

Answers
Answer:
I can not see the full question
Step-by-step explanation:
Answer:
12/20 is 3/5, 42/66= 7/11, 7/56=1/8, 30/45=2/3, 9a/50a= i dont know because you are not able to divide 9/2 and is able to divide 50/2, 125/625= 1/5
Step-by-step explanation:
divide the numerator and the denominator buy the same number to get the answer i got 12/20 to 3/5 because 12/4= 3 and 20/4=5.
he cycle time for trucks hauling concrete to a highway construction site is uniformly distributed over the interval 50 to 70 minutes. find the mean and variance of the cycle times for the trucks.
Answers
The mean cycle time for the trucks hauling concrete to a highway construction site is 60 minutes, and the variance of the cycle times is 100/3 minutes squared.
The cycle time for the trucks hauling concrete is uniformly distributed over the interval 50 to 70 minutes. This means that any value within the interval has an equal chance of being the cycle time for the trucks. The probability density function (PDF) for a uniform distribution is given by:
f(x) = 1/(b-a), for a ≤ x ≤ b
where a = 50 minutes (the lower limit of the interval) and b = 70 minutes (the upper limit of the interval).
To find the mean of the cycle times, we can use the formula:
mean = (a + b)/2
Substituting the values of a and b, we get:
mean = (50 + 70)/2 = 60
Therefore, the mean cycle time for the trucks hauling concrete is 60 minutes.
To find the variance of the cycle times, we can use the formula:
variance = (b - a)² / 12
Substituting the values of a and b, we get:
variance = (70 - 50)² / 12 = 100/3
Therefore, the variance of the cycle times for the trucks hauling concrete is 100/3 minutes squared.
To know more about variance here
https://brainly.com/question/14116780
#SPJ4
There are 5 white balls,8 red balls ,7 yellow balls and 4 green balls in a container a ball is choosen at random.what is the probabilty of chooseing neither white or green? .
Answers
15/19 + 14/19 = 29/19
Step-by-step explanation:
Add the number of balls in the basket together.
Subtract the number of white balls from the sample space ( the total amount of balls) your answer is written over the sample space and the same process is done for the green ball
I need three examples on how math is used in psychology.
Answers
Answer: 1) Error response times
2) Memory Scanning, visual search
3) Stimulus identification
Step-by-step explanation:1) response times reflext the time it takes to interpret a stimulus,get info from memory, initiate a muscle response
2) The hippocampus retrieves info from the working memory and begins to change the brains physical neural wiring
3) A decisive role in our perception and cognition
In general, there are two areas of psychology where mathematics is heavily utilized: mathematical modeling of psychological theories and experimental phenomena, which gives rise to mathematical psychology, and statistical approaches to quantitative measurement practices in psychology, which give rise to psychometrics.
Triangle ARE congruent triangle ___ by ____

Answers
Answer: yes by SSS
hit the like button if it is correct :D
the length of one side of a rectangle is p cm and width is 3(p-2) cm the perimeter is 44 cm find the length and width of rectangle
Answers
Answer:
Length = 7cm, Width = 15cm
Step-by-step explanation:
Length = p
Width = 3(p-2)
= 3p-6
Perimeter = length + width + length + width
= p + 3p-6 + p + 3p-6
= 8p-12
8p - 12 = 44
Isolate 8p.
8p = 44+12
= 56
Find p.
p = 56 ÷ 8
p = 7
Length = 7cm
Width = 3(7)-6
= 21-6
= 15cm
What sorting algorithms are not comparison based?
Answers
The sorting algorithms that are not comparison based are counting sort, bucket sort, and radix sort.
Counting sort works by counting the number of occurrences of each element in an array and then using this information to determine the position of each element in the sorted array.
Bucket sort works by dividing the array into a number of smaller arrays, called buckets, and then sorting each of these smaller arrays separately.
Radix sort works by sorting the elements of an array based on the individual digits of each element, starting with the least significant digit and working up to the most significant digit.
These algorithms do not rely on comparisons between elements, which is why they are not considered comparison based.
To know more about sorting algorithms click on below link:
https://brainly.com/question/14531150#
#SPJ11
Find the slope of the line that passes through the points A(-3, 1) and B(2, -5).
Answers
Answer:
\(m = \frac{ - 5 - 1}{2 - ( - 3)} = - \frac{6}{5} \)
the top-selling red and voss tire is rated 80,000 miles. in fact, the distance the tires can run until they wear out is a normally distributed random variable with a mean of 94,000 miles and a standard deviation of 7200 miles. what is the probability that a tire wears out before 80,000 miles?
Answers
the probability that a top-selling red and voss tire wears out before 80,000 miles is about 2.56%.
The student question asks about the probability that a top-selling red and voss tire, rated for 80,000 miles, wears out before reaching 80,000 miles. The tire's lifespan follows a normal distribution with a mean of 94,000 miles and a standard deviation of 7200 miles.
To find the probability, we need to calculate the z-score first. The z-score is a measure of how many standard deviations away from the mean a particular value is. We can use the following formula to calculate the z-score:
z = (X - μ) / σ
where X is the value (in this case, 80,000 miles), μ is the mean (94,000 miles), and σ is the standard deviation (7200 miles).
Calculate the z-score:
z = (80,000 - 94,000) / 7200
z = -14,000 / 7200
z ≈ -1.944
The z-score is approximately -1.944, which means the tire wearing out at 80,000 miles is about 1.944 standard deviations below the mean.
Find the probability:
Now, we can use the z-score to find the probability. We can look up the z-score in a standard normal distribution table or use a calculator with a built-in function for this purpose.
Using a standard normal distribution table or calculator, we find that the probability corresponding to a z-score of -1.944 is approximately 0.0256 or 2.56%.
for more questions on probability
https://brainly.com/question/24756209
#SPJ11
Convert the polar coordinate (9,(11pi)/6) to Cartesian coordinates. X = y =
Answers
The Cartesian coordinates for the polar coordinate (9, (11π)/6) are x = (9√3)/2 and y = 9/2.
To convert a polar coordinate to Cartesian coordinates, we use the formulas:
x = r * cos(theta)
y = r * sin(theta)
Given the polar coordinate (9, (11π)/6), where r = 9 and θ = (11π)/6, we can substitute these values into the formulas:
x = 9 * cos((11π)/6)
y = 9 * sin((11π)/6)
To simplify, let's recall the values of cosine and sine for (11π)/6. In the fourth quadrant, the reference angle for (11π)/6 is π/6. We know that cos(π/6) = √3/2 and sin(π/6) = 1/2.
Substituting these values into the formulas:
x = 9 * (√3/2)
y = 9 * (1/2)
Simplifying further:
x = (9√3)/2
y = 9/2
Therefore, the Cartesian coordinates for the polar coordinate (9, (11π)/6) are x = (9√3)/2 and y = 9/2.
Learn more about polar coordinate here
https://brainly.com/question/29840804
#SPJ11
differentiate the following function f(x)=2x3 6x-1/x 3ex-sin(x)
Answers
The differentiation of the function is f'(x) = 6x² + 6 - ln(x) + 3eˣ - cos(x)
How to differentiate the functionfrom the question, we have the following parameters that can be used in our computation:
f(x) = 2x³ + 6x - 1/x + 3eˣ - sin(x)
The derivative of the functions can be calculated using the first principle which states that
if f(x) = axⁿ, then f'(x) = naxⁿ⁻¹
Using the above as a guide, we have the following:
f'(x) = 6x² + 6 - ln(x) + 3eˣ - cos(x)
Hence, the differentiation of the function is f'(x) = 6x² + 6 - ln(x) + 3eˣ - cos(x)
Read more about derivatives at
brainly.com/question/5313449
#SPJ4
Quick algebra 1 question for 10 points!
Only answer if you know the answer, quick shout-out to tariqareesha2 and MrBrainly, tysm for the help!

Answers
The range of the quadratic function y = (2 / 3) · x² - 6 is {- 6, 0, 18, 48}.
What is the range of a quadratic equation?
In this case we have a quadratic equation whose domain is stated. The domain of a function is the set of x-values associated to only an element of the range of the function, that is, the set of y-values of the function. We proceed to evaluate the function at each element of the domain and check if the results are in the choices available.
x = - 9
y = (2 / 3) · (- 9)² - 6
y = 48
x = - 6
y = (2 / 3) · (- 6)² - 6
y = 18
x = - 3
y = (2 / 3) · (- 3)² - 6
y = 0
x = 0
y = (2 / 3) · 0² - 6
y = - 6
x = 3
y = (2 / 3) · 3² - 6
y = 0
x = 6
y = (2 / 3) · 6² - 6
y = 18
x = 9
y = (2 / 3) · 9² - 6
y = 48
The range of the quadratic function y = (2 / 3) · x² - 6 is {- 6, 0, 18, 48}.
To learn more on functions: https://brainly.com/question/12431044
#SPJ1
I need this asap please
