-2x^2(3x - 6)
options to choose from
6x^3 + 12x^2
6x^3 - 12x^2
-6x^3 + 12x^2
-6x^3 - 12x^2
Answers
Related Questions
Perimeter of ABC is 67.
ADC is equilateral and ABC is isosceles. Angle CAB=60, ACB=60 and ACB=60. Find perimeter of triangle ADC.
(Triangle ADB intersects at an angle of 60 deg in triangle ABC.)
Answers
Answer:
man can u send the pic of the diagram I will solve it
Flynn has $12 and he earns $8 for every hour he works. Which equation shows how many dollars, d, that Flynn has after h hours.
Answers
Special angles type 1

Answers
Answer:
∠ 1 = 60°
Step-by-step explanation:
the angle on the circle is half the measure of the central angle , subtended on the same arc , then
∠ 1 = \(\frac{1}{2}\) × 120° = 60°
NEED NEED HELP QUICK ASAP

Answers
Answer:
1/3 of the 342 seats which would be 267 of the seats are used by the Students
Step-by-step explanation:
In the diagram shown, m_3 = 3x - 16 and m_4 = x + 84. Find the value of x. o 25 50 34 28

Answers
Answer:
50
Step-by-step explanation:
m3 and m4 are going to be equaivalent due to some law I don't remember the name of.
So, 3x-16 = x+84
(do some rearranging)
2x=100
x=50
Part A: Virginia earned $14 walking her neighbors' dogs on Saturday. She earned some extra money on Sunday doing the same thing. Write an expression with a variable that shows the total amount of money Virginia earned Saturday and Sunday.
Part B: Virginia was able to walk 2 less than twice as many dogs as her friend Alicia. Write an algebraic expression to represent the number of dogs Virginia walked compared with Alicia.
Answers
Cory, Josh and Dan went shopping for Halloween treats. Cory bought 3 chocolate pumpkins, 4 masks and 8 candy witches. He spent $36.65. Josh bought 5 chocolate pumpkins,3 masks and 10 candy witches. He spent $37.50. Dan bought 4 chocolate pumpkins, 5 masks and 6 candy witches. He spent $43.45. Write a system of equations to represent this problem.
Answers
Answer:
\(\left\{\begin{matrix}3x+4y+8z=36.65\\ 5x+3y+10z=37.50\\ 4x+5y+6z=43.35\end{matrix}\right.\)
Step-by-step explanation:
System of equations
Let's set the following variables:
x=Price of chocolate pumpkins
y=Price of masks
z=Price of candy witches
We'll establish the system of equations needed to know the prices of all the Halloween treats.
Cory bought 3 chocolate pumpkins, 4 masks, and 8 candy witches and he spent $36.65. This leads to the following equation:
\(3x+4y+8z=36.65\qquad\qquad [1]\)
Josh bought 5 chocolate pumpkins, 3 masks, and 10 candy witches and he spent $37.50. This leads to the following equation:
\(5x+3y+10z=37.50\qquad\qquad [2]\)
Dan bought 4 chocolate pumpkins, 5 masks, and 6 candy witches and he spent $43.45. This leads to the following equation:
\(4x+5y+6z=43.35\qquad\qquad [3]\)
Collecting the equations [1] [2] [3], we form the system of equations to represent this problem:
\(\left\{\begin{matrix}3x+4y+8z=36.65\\ 5x+3y+10z=37.50\\ 4x+5y+6z=43.35\end{matrix}\right.\)
using the fact that v1 · v2 = v1t v2, show that the dot product of two free vectors does not depend on the choice of frames in which their coordinates are defined
Answers
The dot product of two free vectors is independent of the choice of frames, as it relies only on the inner product of their transposed coordinate vectors.
The dot product of two free vectors, v1 and v2, can be expressed as the inner product of their transposed coordinate vectors, v1t and v2. This inner product is invariant under changes of frames, i.e. the same result will be obtained regardless of the choice of frames in which the coordinates are defined. This is because the transpose of a vector only changes the order of the coordinates, and the inner product of two vectors is unaffected by this reordering. Therefore, the dot product of two free vectors does not depend on the choice of frames in which their coordinates are defined.
Learn more about vectors here
https://brainly.com/question/30202103
#SPJ4
Ok last one,
Find the x-intercept of the following equation. Simplify your answer.
4x + 13y = 6
x-intercept =
Answers
Answer:
x-intercept = 6/4 = 3/2 = 1.50000
Step-by-step explanation:
Rearrange:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
4*x+13*y-(6)=0
Step 1: Equation of a Straight Line
Solve 4x+13y-6 = 0
Tiger recognizes that we have here an equation of a straight line. Such an equation is usually written y=mx+b ("y=mx+c" in the UK).
"y=mx+b" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis.
In this formula :
y tells us how far up the line goes
x tells us how far along
m is the Slope or Gradient i.e. how steep the line is
b is the Y-intercept i.e. where the line crosses the Y axis
The X and Y intercepts and the Slope are called the line properties. We shall now graph the line 4x+13y-6 = 0 and calculate its properties
Graph of a Straight Line :
Calculate the Y-Intercept :
Notice that when x = 0 the value of y is 6/13 so this line "cuts" the y axis at y= 0.46154
y-intercept = 6/13 = 0.46154
Calculate the X-Intercept :
When y = 0 the value of x is 3/2 Our line therefore "cuts" the x axis at x= 1.50000
x-intercept = 6/4 = 3/2 = 1.50000
Calculate the Slope :
Slope is defined as the change in y divided by the change in x. We note that for x=0, the value of y is 0.462 and for x=2.000, the value of y is -0.154. So, for a change of 2.000 in x (The change in x is sometimes referred to as "RUN") we get a change of -0.154 - 0.462 = -0.615 in y. (The change in y is sometimes referred to as "RISE" and the Slope is m = RISE / RUN)
Slope = -0.615/2.000 = -0.308
Geometric figure: Straight Line
Slope = -0.615/2.000 = -0.308
x-intercept = 6/4 = 3/2 = 1.50000
y-intercept = 6/13 = 0.46154
Rachel withdraws $19 from her bank account once each day for three days. What integer represents the change in the amount in the account? Find the integer that would represent the change in the amount in the account if Rachel deposits $19 into her bank account once each day for three days.
Answers
Answer:
How much did she start with tho???
Step-by-step explanation:
Q3 Estimate the monthly average daily radiation on a horizontal surface \( \mathrm{H} \) in June in Amman given the following : Monthly average hours per day of sunshine in June 10 hours Climate type:
Answers
The estimated monthly average daily radiation on a horizontal surface in June in Amman is approximately 7.35 kWh/m(^2)/day.
To estimate the monthly average daily radiation on a horizontal surface H in June in Amman, we can use the following equation:
\([H = S \times H_s \times \frac{\sin(\phi)\sin(\delta)+\cos(\phi)\cos(\delta)\cos(H_a)}{\pi}]\)
where:
S is the solar constant, which is approximately equal to 1367 W/m(^2);
\(H(_s)\) is the average number of sunshine hours per day in Amman in June, which is given as 10 hours;
(\(\phi\)) is the latitude of the location, which for Amman is approximately 31.9 degrees North;
(\(\delta\)) is the solar declination angle, which is a function of the day of the year and can be calculated using various methods such as the one given in the answer to Q1;
\(H(_a)\) is the hour angle, which is the difference between the local solar time and solar noon, and can also be calculated using various methods such as the one given in the answer to Q1.
Substituting the given values, we get:
\([H = 1367 \times 10 \times \frac{\sin(31.9)\sin(\delta)+\cos(31.9)\cos(\delta)\cos(H_a)}{\pi}]\)
Since we are only interested in the monthly average daily radiation, we can assume an average value for the solar declination angle and the hour angle over the month of June. For simplicity, we can assume that the solar declination angle (\(\delta\)) is constant at the value it has on June 21, which is approximately 23.5 degrees North. We can also assume that the hour angle \(H(_a)\) varies linearly from -15 degrees at sunrise to +15 degrees at sunset, with an average value of 0 degrees over the day.
Substituting these values, we get:
\([H = 1367 \times 10 \times \frac{\sin(31.9)\sin(23.5)+\cos(31.9)\cos(23.5)\cos(0)}{\pi}]\)
Simplifying the equation, we get:
\([H \approx 7.35 \text{ kWh/m}^2\text{/day}]\)
Therefore, the estimated monthly average daily radiation on a horizontal surface in June in Amman is approximately 7.35 kWh/m(^2)/day.
Learn more about "average daily radiation " : https://brainly.com/question/32911494
#SPJ11
Partial Derivative Applications, Vectors and Matrices
If z = F(u, v, w) where u = r 2 , v = −2s 2 , and w = lnr + lns,
find ∂z/∂r and ∂z/∂s.
Answers
The values of ∂z/∂r and ∂z/∂s. These partial derivatives will depend on the specific function F(u, v, w) provided.
To find ∂z/∂r and ∂z/∂s, we need to differentiate z = F(u, v, w) with respect to r and s.
Given that u = r^2, v = -2s^2, and w = ln(r) + ln(s), we can substitute these values into z = F(u, v, w).
So, z = F(r^2, -2s^2, ln(r) + ln(s)).
To find ∂z/∂r, we differentiate z with respect to r while treating s as a constant. This gives us:
∂z/∂r = ∂F/∂u * ∂u/∂r + ∂F/∂w * ∂w/∂r.
Similarly, to find ∂z/∂s, we differentiate z with respect to s while treating r as a constant. This gives us:
∂z/∂s = ∂F/∂v * ∂v/∂s + ∂F/∂w * ∂w/∂s.
Since we don't have the specific function F(u, v, w) mentioned in the question, we cannot determine the values of ∂z/∂r and ∂z/∂s. These partial derivatives will depend on the specific function F(u, v, w) provided.
To know more about partial derivatives, visit:
https://brainly.com/question/28751547
#SPJ11
A certain integer between 1 and 1200 leaves the reminder 1, 2, 6 when divided by 9, 11, 13 respectively. What is the integer?
Answers
An integer between 1 and 1200 leaves remainders of 1, 2, and 6 when divided by 9, 11, and 13, respectively. By finding the least common multiple of these divisors, we can determine the integer. In this case, the integer is 361.
To find the integer that satisfies the given conditions, we need to determine the least common multiple (LCM) of 9, 11, and 13.
First, let's consider the remainders: 1, 2, and 6. These are one less than the respective divisors. We can rewrite them as 9 - 8, 11 - 9, and 13 - 7, respectively.
Next, we calculate the LCM of the divisors: LCM(9, 11, 13) = 9 * 11 * 13 = 1287.
Now, we need to find the remainder when 1287 is divided by 9, 11, and 13. This can be done by subtracting the respective remainders we calculated earlier: 1287 - 8 = 1279 (remainder 1), 1287 - 9 = 1278 (remainder 2), 1287 - 7 = 1280 (remainder 6).
Therefore, the integer that satisfies the conditions is 1287 - (1 + 2 + 6) = 1287 - 9 = 1278.
However, we need to ensure that the integer is within the given range of 1 to 1200. Since 1278 is greater than 1200, we need to subtract the LCM (1287) to get the integer within the range.
1278 - 1287 = -9.
Thus, the integer that satisfies all the given conditions is 1287 - 9 = 1278.
To learn more about least common multiple visit:
brainly.com/question/11533141
#SPJ11
A tudent earned 48 out of 50 point on the lat tet, what percent correct did the tudent earn
Answers
Answer:
96%
Step-by-step explanation:
48 ÷ 50 × 100
A bus leaves a bus station at 9:00 am and travels on the Eastbound Highway. A second bus leaves the same bus station 45 minutes later and travels in the same direction on the same highway at a speed of 20 kilometers per hour faster than the first bus. The second bus catches up with the first bus at 12:00. How fast was each bus traveling? (Include units in your answer. ) A. [3 pts) Define variables to represent the unknowns and setup the necessary equations to answer the question
Answers
The speed of the first bus is 60 km/h while the speed of the second bus is 80 km/h.
SpeedSpeed is the rate of change of distance with time. It is given by:
Speed = distance / time
Let a represent the speed of the first bus, and b represent the speed of the second bus.
b = a + 20
At 12:00, t = 3 hours, hence:
a = d/3
d = 3a
Also:
b = d/2.25
d = 2.25b
3a = 2.25b
3a = 2.25(a + 20)
a = 60
b = 60 + 20 = 80
The speed of the first bus is 60 km/h while the speed of the second bus is 80 km/h.
Find out more on Speed at: https://brainly.com/question/4931057
What are the values of x and y

Answers
Answer:
??
Step-by-step explanation:
Can't see that clear
Nandlal bought 20 dozen notebooks at Rs.156 per dozen.He sold 8 dozens of them at 10% gain and the remaining 12 dozens at 20% gain.What is his gain percent on the whole transaction?
Answers
Answer:
\(8(156 \times 1.1) + 12(156 \times 1.2) \)
Simplify.
68.6³ = 61²]
65
![Simplify.68.6 = 61]65](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/9ScHX0YkaoDpJrGAT2KDMUgEa2h6mkgC.png)
Answers
What is the answer to this fast smart people
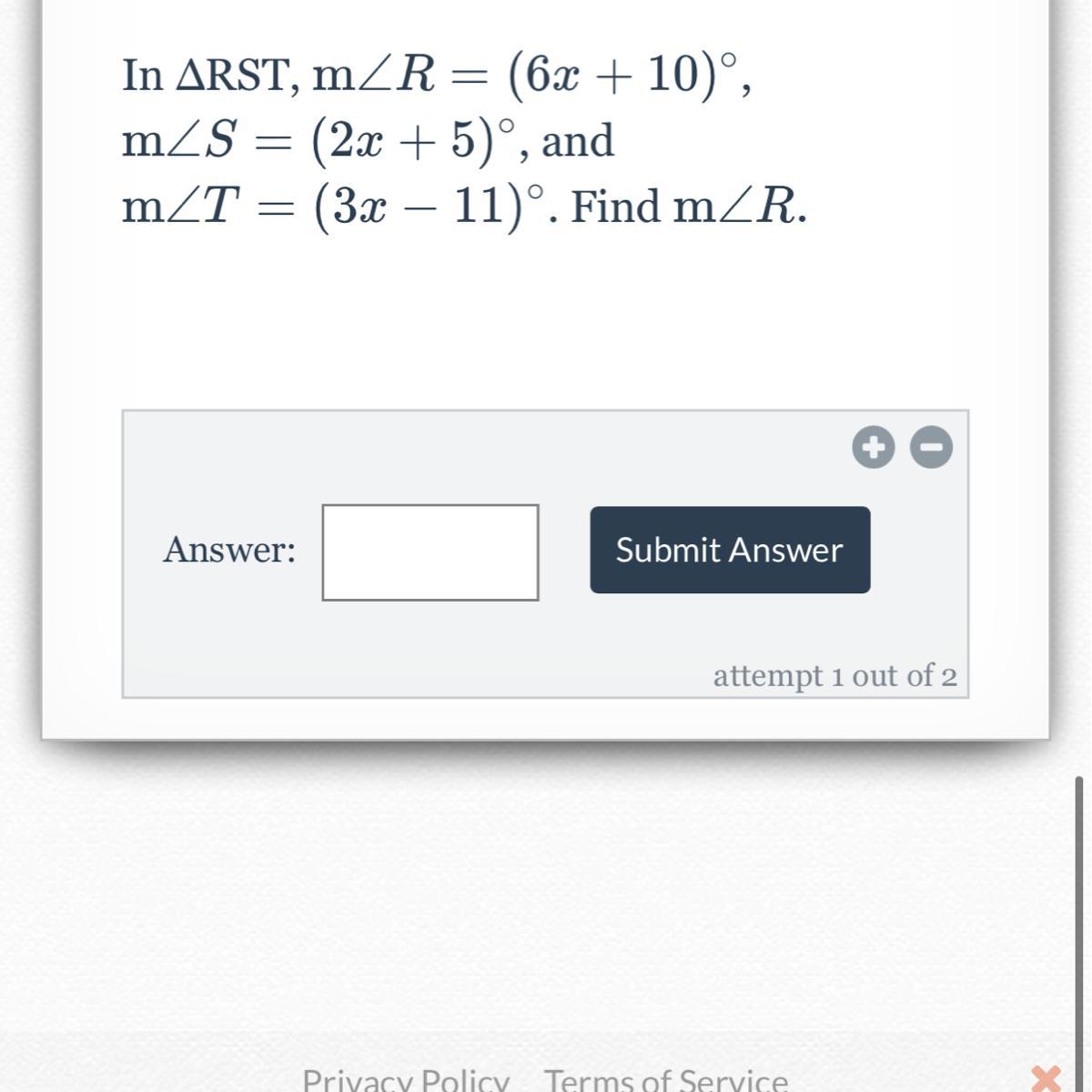
Answers
Answer:
m<R = 106°
Step-by-step explanation:
Given,
m<R = (6x+10)°
m<S = (2x+5)°
m<T = (3x-11)°
Now,
6x+10°+2x+5°+3x-11° = 180°{the sum of angles of triangle is 180°}
or, 11x+4° = 180°
or, 11x = 180°-4
or, x = 176°/11
or, x = 16°
therefore, x = 16°
m<R = (6x+10)°
= 6×16°+10°
= 96°+10°
= 106°
Anne and Beate together have $120, Beate and Cecilie together have $60, and Anne and Cecilie together have $70. How much money do they have in total?
Answers
Answer:
Step-by-step explanation:
$270 in total
find 1 2/3 + (-2 1/2). show your work
Answers
Answer: -5/6
Step-by-step explanation:
(1 + -2) + (2/3+ -1/2)
-1 + 2 x 2 / 3 x 2 + -1 x 3 / 2 x 3
Simplify:
-1 + 4/6 + -3/6
Turn into a simpler fraction:
1 + 4 + (-3) / 6
Combine like terms:
-1 + 1/6
Add together:
- 5/6
Hope this helps!
Write and equation to match each graph
rsm work


Answers
The equation of the graph is y = -| x | + 1
Given data ,
The graph of y = -|x| + 1 is a V-shaped graph with the vertex at the origin (0, 1), and it opens downwards along the y-axis. The negative sign in front of the absolute value function reflects the graph of y = |x| across the x-axis, flipping it upside down.
When x is greater than or equal to 0, the expression |x| becomes x, and the graph of y = -|x| + 1 will be y = -x + 1 for x ≥ 0.
When x is less than 0, the expression |x| becomes -x, and the graph of y = -|x| + 1 will be y = x + 1 for x < 0.
Thus, the graph of y = -|x| + 1 consists of two linear segments with slopes of -1, intersecting at the point (0, 1), and extends indefinitely in both directions along the x-axis.
Hence , the equation of graph is y = -| x | + 1
To learn more about equation of graph of polynomials click :
brainly.com/question/16957172
#SPJ1
Question Content Area
Net Present Value
A project has estimated annual net cash flows of $15,000 for ten
years and is estimated to cost $47,500. Assume a minimum acceptable
rate of return of 20%. Use
Answers
The required rate of return (or minimum acceptable rate of return) is 20 percent. If the net cash flows are $15,000 per year for ten years, the total cash flow is $150,000. The project's cost is $47,500. We can now apply the net present value formula to determine whether or not the project is feasible.
Net Present Value (NPV) = Cash flow / (1 + r)^n - Cost Where, r is the discount rate, n is the number of years, and Cost is the initial outlay.
Net Present Value = 150000 / (1 + 0.20)^10 - 47500
Net Present Value = $67,482.22
Since the NPV is positive, the project is feasible. When calculating net present value, it's important to remember that a positive NPV implies that the project is expected to generate a return that exceeds the cost of capital, whereas a negative NPV indicates that the project is expected to generate a return that is less than the cost of capital, and as a result, it should be avoided.
Know more about NPV here:
https://brainly.com/question/32720837
#SPJ11
Jodie started washing her car at 10:15 am she finished at 10:50 am how long did it take jody to wash her car.
Answers
Answer:
35 minutes
Step-by-step explanation:
this requires us to find out how long it took and because both times given to figure this out are within the same hour it is easy to figure out in this case, 50 - 15 = 35. This is not as simple with all problems like this but because of the times given in this problem its much easier.
Suppose the sample mean CO2CO2 level is 418 ppm.418 ppm. Is there any evidence to suggest that the population mean CO2CO2 level has increased
Answers
The probability that sample is greater than 418 will be is 6.533.
What is a probability?Probability is the occurence of likely events. It is the area of mathematics that deals with numerical estimates of the likelihood that an event will occur or that a statement is true.
Here we have
\(\mu=397.64,n=40,\sigma=20\)
According to central limit theorem, the sampling distribution of mean will be normal with mean
\(\mu_{\bar{x}}=\mu=397.64\)
and standard deviation
\(\sigma_{\bar{x}}=\frac{\sigma}{\sqrt{n}}=\frac{20}{\sqrt{40}}=3.1623\)
The z-score for\(\bar{x}=418\) is
\(z=\frac{\bar{x}-\mu_{\bar{x}}}{\sigma_{\bar{x}}}=\frac{418-397.34}{3.1623}=6.533\)
Therefore, the probability that sample is greater than 418 will be
\(P(\bar{x} > 418)=P(z > 6.533)\)
Learn more about probability here:
https://brainly.com/question/29557037
#SPJ4
Incomplete Question
Carbon dioxide (CO2) is one of the primary gases contributing to the greenhouse effect and global warming. The mean amount of CO2 in the atmosphere for March 2013 was 397.34 parts per million (ppm). Suppose 40 atmospheric samples are selected at random in May 2013 and the standard deviation for CO2 in the atmosphere is σ = 20 ppm. (1 pt.)
c) Suppose the sample mean CO2 level is 400. Is there any evidence to suggest that the population mean CO2 level has increased?
The method of tree-ring dating gave the following years A.D. for an archaeological excavation site. Assume that the population of x values has an approximately normal distribution. 1,320 1,285 1,306 1,306 1,268 1,316 1,275 1,317 1,275
When finding an 90% confidence interval, what is the critical value for confidence level? (Give your answer to three decimal places.)
tc =
What is the maximal margin of error when finding a 90% confidence interval for the mean of all tree-ring dates from this archaeological site? (Round your answer to the nearest whole number.)
E =
Find a 90% confidence interval for the mean of all tree-ring dates from this archaeological site. (Round your answers to the nearest whole number.)
lower limit _______
upper limit _______
Answers
The 90% confidence interval for the mean of all tree-ring dates from this archaeological site is (1295, 1317).
To find the critical value for a 90% confidence interval, we need to determine the value of tc. Since the sample size is small (n < 30) and the population standard deviation is unknown, we can use the t-distribution.
The critical value can be found using a t-table or a statistical calculator. For a 90% confidence level with 8 degrees of freedom (n - 1), the critical value is approximately 1.860.
tc = 1.860
To find the maximal margin of error, we can use the formula:
E = tc * (s / √n)
where s is the sample standard deviation and n is the sample size. Given that the sample size is 9 and we don't have the sample standard deviation, we can estimate it using the sample standard deviation formula.
After calculating the sample standard deviation, let's assume it is s = 18.45 (rounded to two decimal places).
E = 1.860 * (18.45 / √9) = 11.079
The maximal margin of error is approximately 11.
To find the confidence interval, we use the formula:
lower limit = sample mean - E
upper limit = sample mean + E
Given that the sample mean is 1306 (rounded to the nearest whole number):
lower limit = 1306 - 11 = 1295
upper limit = 1306 + 11 = 1317
Know more about 90% confidence interval here:
https://brainly.com/question/31420373
#SPJ11
A recently televised broadcast of a popular television show had a 15 share, meaning that among 5000 monitored households with TV sets in use, 15% of them were tuned to the show. A 0.01 significance level is used to test an advertiser’s claim that among the households with TV sets in use, less than 20% were tuned in to the show. Find the P-value.
1.9998
0.9999
0.0001
0.0002
Answers
The p-value of the given hypothesis is; 0.9999
How to find the p-value of the statistics?The formula for the z-score of proportions is;
z = (p^ - p)/√(p(1 - p)/n)
where;
p^ is sample proportion
p is population proportion
n is sample size
We are given;
p^ = 15% = 0.15
p = 20% = 0.2
n = 5000
Thus;
z = (0.15 - 0.2)/√(0.2(1 - 0.2)/5000)
z = -8.8388
From p-value from z-score calculator, we have;
P(Z < -8.8388) = 1 - 0.0001 = 0.9999
Read more about p-value at; https://brainly.com/question/4621112
#SPJ1
What is the remainder when x 3 1 is divided by x 3 x 1?
Answers
The remainder when x³ - 1 is divided by (x + 3) is -28
How to determine the remainder of the polynomial division?The functions are given as
x 3 1 is divided by x 3
Rewrite them as
f(x) = x³ - 1 is divided by (x + 3)
Set the divisor to 0
So, we have
x + 3 = 0
Determine the value of x
This gives
x = -3
By the remainder theorem
Substitute x = -3 in the function f(x)
So, we have
f(-3) = (-3)³ - 1
Evaluate the expression
f(-3) = -28
By the remainder theorem, this represents the remainder
Read more about remainder at
brainly.com/question/14130807
#SPJ1
Determine if the following pairs of lines are parallel, perpendicular, or neither.
x+y = -3
x+y = 5
Answers
y= -x - 3
y= -x + 5
Since both of these linear equations have the same slope but a different y-intercept, they are parallel, meaning they will go on forever without intersecting. A line would be perpendicular if the slope is opposite reciprocal to the other equation.
Hope this helps!
How many solutions does the equation: 4x-8=2(2x-4) have?