-2x+y=1 solve with steps
Answers
Answer:
x=1 and y=3
Step-by-step explanation:
-2x1=-2
-2+3=1
So this answer makes sense
Answer:
y = 2x + 1
Step-by-step explanation:
Given: -2x+y=1
Add 2x to both sides: y=1+2x
Reorder: y = 2x + 1
I am not sure exactly what you need for this point, but here is the equation in y=mx+b form aka slope-intercept form
m = slope = 2
b = y-intercept = 1
Hope this helps, have a nice day :D
Related Questions
Describe the domain of
y = 3(1/2)^x
Answers
Answer:
Step-by-step explanation:

On a coordinate plane, circle has its center at the point (3, −6). The point (−1, −2) is on circle .
Which of these statements are correct? Choose ALL that are correct.
Responses
The line = − 1 is tangent to circle at P
The line = − 1 is tangent to circle at P
The area of the circle is 32 square units
The area of the circle is 32 square units
The radius of the circle is 4√2
The radius of the circle is 4√2
The range of the circle is (−6 − 4√2) ≤ ≤ (−6 + 4√2) -
The range of the circle is (−6 − 4√2) ≤ ≤ (−6 + 4√2) -
The point (4, −0.5) is on the circle.
The point (4, −0.5) is on the circle.
The equation of the circle is ( − 3)² + ( + 6)² = 32

Answers
We can conclude that the equation of the circle is (x - 3)² + (y + 6)² = 32, where (3, -6) is the center and 4√2 is the radius. Option 3 and 6 are correct options.
Based on the information given, we know that circle has its center at the point (3, -6) and a radius of 4√2. We also know that the point (-1, -2) and (4, -0.5) are on the circle.
Using the distance formula, we can confirm that the distance between the center of the circle and each of these points is indeed 4√2.
This equation can be simplified to x² - 6x + y² + 12y + 1 = 0 by expanding and combining like terms. This is the equation of circle , and any point that satisfies this equation will be on the circle. Option 3 and 6 are correct options.
To learn more about : equation
https://brainly.com/question/17145398
#SPJ11
I need help with figuring out the meters …

Answers
Step-by-step explanation:
length = 7m or 5m
width= 5m or 7m
Express 75 as a product of its prime factors write the prime factors in ascending order and give your answer in index form
Answers
Step-by-step explanation:
75 = 3 x 5 x 5 in prime factorization
Answer:
Step-by-step explanation:
3x5x5
Two tickets to the movies cost $16. If two drinks add $4.56 to the total, how much change should be received from $25?
Answers
Answer:
total cost =$ 16 +$ 4.56=$ 20.56
change received = $25 - $ 20.56 = $4.44 .
Step-by-step explanation:
therefore your answer is 4,44 hope this helps
HELP PLEASE I DONT GET THIS

Answers
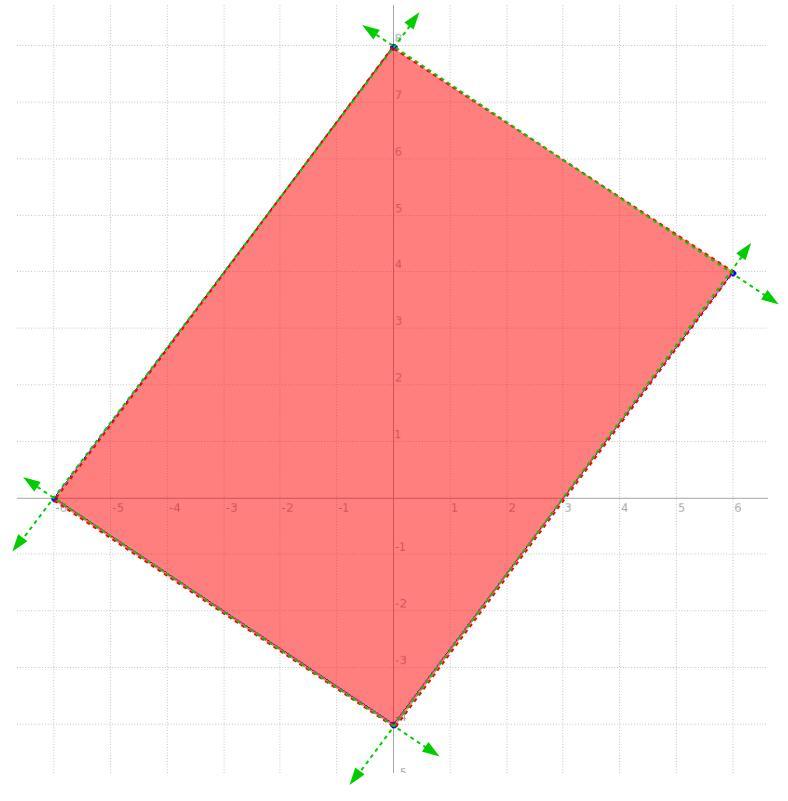
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.
we have a line passing through (-6,0) and (0,8), side one
we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two
we have a line passing through (0,-4) and (6,4), side three
now, side four is simply the line connecting one and three.
the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?
well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)
\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)
now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to (-3 , 4). Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.
now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality
\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)
haydenkyletoddhaydenkyletodd
Answers
Alguém me ajuda pelo amor de Deus q eu tô em prova

Answers
Answer:
\(x=50\º\)
Step-by-step explanation:
We know ∠R+∠S+∠T = 180º
Then,
\((x+50\º)+(x+10\º)+(x-30\º) = 180\º\)
\(3x+30\º = 180\º\)
\(3x = 150\º\)
\(x=50\º\)
Which of the following is the function of FX if F^-1 (x) = ×/8 +3
Answers
Answer:
F(x)=8(x-3)
Step-by-step explanation:
Had to watch a video but I THINK this is the correct answer
Simplify 3^2 • 3^5. PLZ HELP FAST WILL GIVE BRAINLIEST

Answers
Answer:
1 2/13
Step-by-step explanation:
Explanation: have a good day/night :)
A farmer uses x lb of fertilizer per acre at a cost of 1.4 per pound, leading to a revenue of R = 700 – 400e -x/100 dollars per acre.
(a) How many pounds of fertilizer should be applied per acre to maximize profit? Write you answer in decimal form rounding to three decimal places
Number
pounds per acre.
(b) What is the maximum profit on a 200 acre farm?
$ Number
Answers
Answer:
The cost can be written as:
C(x) = $1.4*x
The revenue can be written as:
R(x) = $700 - $400*e^(-x/100)
And as you know, the profit is written as the difference between the revenue and the cost:
P(x) = R(x) - C(x)
P(x) = $700 - $400*e^(-x/100) - $1.4*x
Now we want to maximize this, then we must look at the zeros in the derivate of P(x)
dP/dx = P'(x) = (-1/100)*$400*e^(-x/100) - $1.4
The maximum will be when P'(x) = 0.
we can solve:
0 = (-1/100)*$400*e^(-x/100) - $1.4
$1.4 = (-1/100)*$400*e^(-x/100)
(-100)*$1.4 = $400*e^(-x/100)
$140 = $400*e^(-x/100)
($140/$400) = e^(-x/100)
0.35 = e^(-x/100)
Now we can apply the Ln() in both sides and get:
ln(0.35) = ln(e^(-x/100) ) = -x/100
-ln(0.35)*100 = x = 104.98
You should apply 104.90 pounds of fertilizer.
b) The profit per acre, is:
P(x) = $700 - $400*e^(-x/100) - $1.4*x
Then if you have 200 acres, the profit will be:
200*P(x) = 200*($700 - $400*e^(-x/100) - $1.4*x)
and the maximum profit is whit x = 104.98 pounds, then:
200*P(104.98) = 200*($700 - $400*e^(-104.98/100) - $1.4*104.98) = $82,604.98
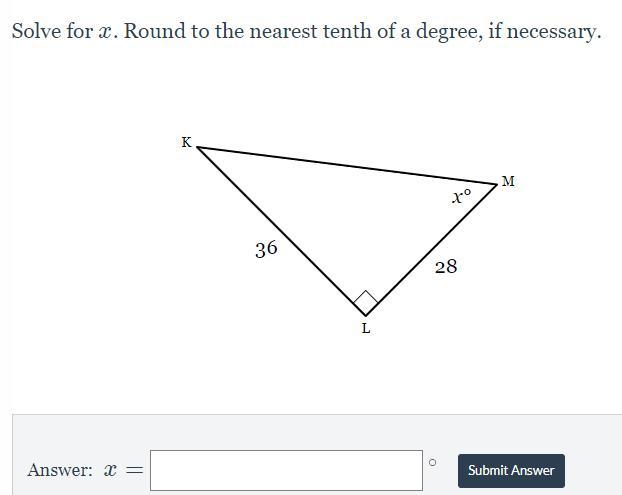
The measures of the angles of a triangle are shown in the figure below. Solve for x.

Answers
Answer:
x=5
Step-by-step explanation:
We know that the angels in a triangle are equal to 180.
(6x+20)+(7x-10)+105=180
We open the prentices and simplify.
13x+115=180
Now we can subtract 115 on both sides.
13x=65
At last, we can divide by 13 on both sides to get the result of x.
x=5
2x − y < 4
x + y > −1
In each graph, the area for f(x) is shaded and labeled A, the area for g(x) is shaded and labeled B, and the area where they have shading in common is labeled AB.
Answers
The graph should visually represent the shaded regions A and B, as well as their overlap in region AB. It's important to note that without a specific scale or values, the graph may not accurately depict the exact shape and position of the shaded regions.
To graph the system of inequalities 2x - y < 4 and x + y > -1, we can start by graphing each inequality separately and then determining the overlapping region.
For the inequality 2x - y < 4:
Start by graphing the line 2x - y = 4. Choose two points on the line, such as (0, -4) and (2, 0), and connect them to draw the line.
Since the inequality is "less than" (<), shade the region below the line. Label this shaded region as A.
For the inequality x + y > -1:
Graph the line x + y = -1 using points such as (-2, 1) and (0, -1). Connect the points to draw the line.
Since the inequality is "greater than" (>), shade the region above the line. Label this shaded region as B.
Finally, identify the overlapping region of the shaded regions A and B. This region represents the solution to the system of inequalities and is labeled as AB. This region indicates the values of x and y that satisfy both inequalities simultaneously.
For more such questions on graph visit;
https://brainly.com/question/19040584
#SPJ8
Answer:
Step-by-step explanation:
2x − y < 4
x + y > −1
In each graph, the area for f(x) is shaded and labeled A, the area for g(x) is shaded and labeled B, and the area where they have shading in common is labeled AB.
The coordinates of the point 3/10 of the way from A to B are _

Answers
Answer:
(-1, -4.8)
Step-by-step Explanation:
Let the point be P, which is 3/10 of the way from A to B. This means, it divides P into AP and PB in the ratio, 3:10 = AP/PB = 3/10.
Apply the formula for internal division to find the coordinates which is given as:
\( x = \frac{mx_2 + nx_1}{m + n} \)
\( y = \frac{my_2 + ny_1}{m + n} \)
Where,
\( A(-4, -8) = (x_1, y_1) \)
\( B(9, 6) = (x_2, y_2) \)
\( m = 3, n = 10 \)
Plug in the necessary values to find x and y coordinates for point P
\( x = \frac{mx_2 + nx_1}{m + n} \)
\( x = \frac{3(9) + 10(-4)}{3 + 10} \)
\( x = \frac{27 - 40}{13} \)
\( x = \frac{-13}{13} \)
\( x = -1 \)
\( y = \frac{my_2 + ny_1}{m + n} \)
\( y = \frac{3(6) + 10(-8)}{3 + 10} \)
\( y = \frac{18 - 80}{13} \)
\( y = \frac{-62}{13} \)
\( y = \frac{-62}{13} \)
\( y = -4.8 \)
The coordinates of the point 3/10 of the way from A to B are (-1, -4.8)
Answer:
(0.2,-2.3)
Step-by-step explanation:
The US Census reported that it takes workers an average of 28 minutes to get home from work with standard deviation 5 minutes. A random sample of 10 workers in a large metropolitan area showed an average time to get home from work to be 32 minutes. Is this evidence that workers in the large city take longer than 28 minutes to get home from work.
Answers
Using the z-distribution, as we have the standard deviation for the population, to test the hypothesis, it is found that this is evidence that workers in the large city take longer than 28 minutes to get home from work.
What are the hypothesis tested?At the null hypothesis, it is tested if the mean time is of 28 minutes, that is:
\(H_0: \mu = 28\)
At the alternative hypothesis, it is tested if the mean time is greater than 28 minutes, that is:
\(H_1: \mu > 28\).
What is the test statistic?The test statistic is given by:
\(z = \frac{\overline{x} - \mu}{\frac{\sigma}{\sqrt{n}}}\)
The parameters are:
\(\overline{x}\) is the sample mean.\(\mu\) is the value tested at the null hypothesis.\(\sigma\) is the standard deviation of the sample.n is the sample size.In this problem, the values of the parameters are given by:
\(\overline{x} = 32, \mu = 28, \sigma = 5, n = 10\)
Hence:
\(z = \frac{\overline{x} - \mu}{\frac{\sigma}{\sqrt{n}}}\)
\(z = \frac{32 - 28}{\frac{5}{\sqrt{10}}}\)
\(z = 2.53\)
What is the decision?Considering that we have a right-tailed test, as we are testing if the mean is greater than a value, with a standard significance level of 0.05, the critical value is of \(z^\ast = 1.645\).
Since the test statistic is greater than the critical value, it is found that this is evidence that workers in the large city take longer than 28 minutes to get home from work.
To learn more about the z-distribution, you can check https://brainly.com/question/26454209
how can 12 people share 7 apples so that each apple is cut into equal pieces only and into no more than 4 pieces? It also must be fair!
Answers
Answer:
1.75 or 1 3/4 pieces each
Step-by-step explanation:
3 pieces per apple x 7 = 21
21/12 = 1.75
The solution is 1/4 + 1/3 = 7/12
The number of apples is shared among 12 people is given by the equation A = ( 1/4 ) + ( 1/3 ) = 7/12
What is an Equation?
Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Let the number of apples be = 7 apples
Let the number of people be = 12 people
Now , let the number of apples each person gets be A = number of apples / number of people
Substituting the values in the equation , we get
Number of apples each person gets be A = 7/12
Now , the value 7/12 is represented as A = 1/12 + 6/12
And, cut 4 apples into thirds and cut 3 apples into fourths
Substituting the values in the equation , we get
A = ( 1/4 ) + ( 1/3 ) be equation (1)
On simplifying the equation , we get
A = ( 3 + 4 ) / ( 3 x 4 )
A = 7 / 12
Therefore , the value of A is 7/12
Hence , the number of apples shared is A = ( 1/4 ) + ( 1/3 )
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ2
A 2-column table with 5 rows. Column 1 is labeled Evelyn's Scores with entries 125, 137, 138, 145, 145. Column 2 is labeled Distance from the Mean with entries x, y, 0, 7, z.
What is the mean absolute deviation of Evelyn’s scores?
5.1
5.6
5.8
7
Answers
Answer:
Column 1(X) Column 2(mean - X)
125 -13
137 -1
138 0
145 7
145 7
Mean = 138
Mean Absolute Deviation : 5.6
Answer:
for all the lazy readers on top the answer is.. B. 5.6:)
Step-by-step explanation:
determine what type of model bets fits the given situation: A $500 raise in salary each year
Answers
The type of model that best fits the situation of a $500 raise in salary each year is a linear model.
In a linear model, the dependent variable changes a constant amount for constant increments of the independent variable.
In the given case, the dependent variable is the salary and the independent variable is the year.
You may build a table to show that for increments of 1 year the increments of the salary is $500:
Year Salary Change in year Change in salary
2010 A - -
2011 A + 500 2011 - 2010 = 1 A + 500 - 500 = 500
2012 A + 1,000 2012 - 2011 = 1 A + 1,000 - (A + 500) = 500
So, you can see that every year the salary increases the same amount ($500).
In general, a linear model is represented by the general equation y = mx + b, where x is the change of y per unit change of x, and b is the initial value (y-intercept).
In this case, m = $500 and b is the starting salary: y = 500x + b.
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

(x+2) (x+3) + (x-3) (x-2)-2x (x+1)=0
Answers
Answer:
Step-by-step explanation:
x(x+3) + 2(x+3) + x(x-2) - 3(x-2) - 2x2 - 2x =0
x2 + 3x + 2x + 6 + x2 - 2x - 3x + 6 - 2x2 - 2x = 0
x2 + x2- 2x2 + 3x + 2x - 2x - 3x - 2x + 6 + 6 = 0
2x2 - 2x2 - 2x + 12 =0
-2x = -12
X = -12/-2
X = 6
here, x2 is x squared.
Noise levels at 5 airports were measured in decibels yielding the following data:
117,118,140,116,119
1. Construct the 90% confidence interval for the mean noise level at such locations. Assume the population is approximately normal.
2. Calculate the sample mean for the given sample data.
3. Find the critical value that should be used in constructing the confidence interval.
Answers
Answer:
1. 112.364<μ,131.636
2. mean = 122
3. critical value = +-2.1318
Step-by-step explanation:
117+118+140+116+119/5
= 610/5
= 122
the sample mean = 122
the sample standard deviation
s² = (117-122)²+(118-122)²+(140-122)²+(116-122²)+(119-122)²/5-1
= 25+16+324+36+9/4
= 410/4
= 102.5
s² = 102.5
s = √102.5
s= 10.12
SE = s/√n
= 10.12/√5
= 4.52
degree of freedom = 5-1 = 4
critical value of t = +-2.1318 using soft ware
confidence interval =
mean +- t(SE)
122-(2.1318)(4.52), 122+(2.1318)(4.52)
= [112.364, 131.636]
112.364<μ,131.636
therefore these are the answers in the ordre it was given in the question
1. 112.364<μ,131.636
2. mean = 122
3. critical value = +-2.1318
Find unit rate $602 for 20 hours of work
Answers
Sasha is dividing 1/4 pound of peanuts into 5 plastic bags. What fraction of a pound of peanuts will be in each plastic bag?
Answers
Answer:
1/20
Step-by-step explanation:
(1/4)/5= (1/4)/(5/1)
You cross multiply and you get 1/20
3. Given the directed line segment AB, with endpoints A20, 6) and B(-16, 50), find the point Q
that partitions this segment into a 1:1 ratio.
Answers
The point Q that partitions the line segment is Q(2,28)
Given that the directed line segment AB, with endpoints A(20, 6) and B(-16, 50) and divide the segment into a 1:1 ratio.
A line segment is a part of a line bounded by two distinct endpoints and containing all the points of the line segment between its endpoints.
We will find the point Q by using the section formula that is
Q(x,y)=((mx₂+nx₁)/(m+n),(my₂+ny₁)/(m+n))
The given ratio is m:n=1:1 and the points (x₁,y₁)=(20,6) and (x₂,y₂)=(-16,50).
Firstly, we will find the point Q for x-axis, we get
Q(x)=(mx₂+nx₁)/(m+n)
Q(x)=(1×(-16)+1×20)/(1+1)
Q(x)=(-16+20)/2
Q(x)=4/2
Q(x)=2
Now, we will find the point Q for y-axis, we get
Q(y)=(my₂+ny₁)/(m+n)
Q(y)=(1×50+1×6)/(1+1)
Q(y)=(50+6)/2
Q(y)=56/2
Q(y)=28
The point Q that partitions the line segment is Q(x,y)=(2,28)
Hence, point Q partitions this segment into a 1:1 ratio with directed line segment AB, with endpoints A(20, 6) and B(-16, 50) is Q(2,28).
Learn more about the line segment from here brainly.com/question/9034900
#SPJ9
can someone help me with my work so i can pass
Answers
The measure of the angles are:: x = 20. so, angles are, 20°, 40°, 120°.
Here, we have,
we know that,
The sum of the angles in a triangle add to 180
x+2x+6x = 180
Combine like terms
9x= 180
Divide by 9
9x/9 = 180/9
x = 20.
Hence, The measure of the angles are:: x = 20. so, angles are, 20°, 40°, 120°.
To learn more on angle click:
brainly.com/question/28451077
#SPJ1
complete question:
The sum of the angle measures in a triangle is 180°. The angles of a certain triangle measure x°, 2x°, and 6x°. Solve for x.
If it takes three robots 17 hours to mow vast lawn how many robots would be needed to mow it under three hours
Answers
Answer:1/4 of robot
Step-by-step explanation:
Write the dual of following problems: Maximize Z = 7X1 + 5X2 Subject to: X1 + 2X2 ≤ 6 4X1 + 3X2 ≤ 12 X1 , X2 ≥ 0 brainly
Answers
The dual problem of the primal problem "Maximize Z = 7X1 + 5X2, Subject to X1 + 2X2 ≤ 6, 4X1 + 3X2 ≤ 12, X1, X2 ≥ 0" is:
What are inequalities?Mathematical expressions with inequalities are those in which the two sides are not equal. Contrary to equations, we compare two values in inequality. Greater than (or greater than or equal to), less than (or less than or equal to), or not equal to signs are used in place of the equal sign.
Minimize Z = 6Y1 + 12Y2
Here
Y1 + 4Y2 ≥ 7
2Y1 + 3Y2 ≥ 5
Y1, Y2 ≥ 0
(b) The dual problem of the primal problem "Maximize Z = 3X1 + 4X2, Subject to 5X1 + 4X2 ≤ 200, 3X1 + 5X2 ≤ 150, 8X1 + 4X2 ≥ 80, X1, X2 ≥ 0" is:
Minimize Z = 200Y1 + 150Y2
Subject to:
4Y1 + 5Y2 ≥ 3
5Y1 + 3Y2 ≥ 4
4Y1 + 8Y2 ≤ -80
Y1, Y2 ≥ 0
To learn more about the inequalities visit:
https://brainly.com/question/20383699.
#SPJ9
"Your question is incomplete, probably the complete question/missing part is:"
Write the dual of following problems:
(a) Maximize Z = 7X1 + 5X2
Subject to:
X1 + 2X2 ≤ 6
4X1 + 3X2 ≤ 12
X1, X2 ≥ 0
(b) Maximize Z= 3X1 + 4X2
Subject to:
5X1 + 4X2 ≤ 200
3X1 + 5X2 ≤ 150
8X1 + 4X2 ≥ 80
X1, X2 ≥ 0
what is 3 2/3 + 2 7/10
Answers
The simplified sum is 191/30.In mixed number form, this is 6 and 11/30.3 2/3 + 2 7/10 equals 6 and 11/30.
To add the mixed numbers 3 2/3 and 2 7/10, we can follow these steps:First, convert both mixed numbers into improper fractions.
3 2/3 = (3 * 3 + 2)/3 = 11/3
2 7/10 = (2 * 10 + 7)/10 = 27/10
Now, we have 11/3 + 27/10.
To find a common denominator, we multiply the denominators: 3 * 10 = 30.Rewriting the fractions with the common denominator, we have 110/30 + 81/30.
Adding the numerators, we get 110 + 81 = 191.
The sum is 191/30.
To simplify the fraction, we can divide both the numerator and denominator by their greatest common divisor, which is 1.
For more such questions on sum
https://brainly.com/question/30432029
#SPJ8
Perry wants to increase their protein intake for a diet. They find a good protein bar that contains 15g of protein per serving. They also find a good protein shake that contains 24g of protein per serving. If Perry wants to add 165g of protein to their diet each week, how many servings of each do they need per week to meet all their protein goals in 8 servings?
Answers
We need 3 servings of protein bars and 5 servings of protein shakes per week.
Given,
Protein bar = 15g of protein per serving.
Protein shake = 24g of protein per serving.
165g of protein is required each week.
Total number of servings = 8
We need to find how many servings of each are needed per week to meet 165g of protein.
How do solve a system of equations?By substitution method.
Let us consider two systems of equations:
x + y = a ____(1)
x + 2y = b ____(2)
From (1) we have,
x = a - y
Putting this in (2) we get,
a - y + 2y = b
y = b - a
Let us consider,
Protein bar servings be x.
Protein shake servings be y.
Make two systems of equations.
x + y = 8 _____(A)
15x + 24y = 165 ______(B)
Solve by substitution method.
From (A),
x = 8 -y
Putting in (B)
15(8-y) + 24y = 165
120 - 15y + 24y = 165
120 + 9y = 165
Subtracting 120 on both sides.
9y = 165 - 120
9y = 45
Dividing both sides by 9
y = 45/9 = 5
We have,
y = 5 putting in (A)
x + y = 8
x = 8 - 5
x = 3.
We can cross-check:
- x + y = 8
5 + 3 = 8
8 = 8
- 15x + 24y = 165
15 x 3 + 24 x 5 = 165
45 + 120 = 165
165 = 165
Thus we need 3 servings of protein bars and 5 servings of protein shakes per week.
Learn more about solving a system of equations here:
https://brainly.com/question/27911202
#SPJ1
Please help I will give brainleist

Answers
Answer: 0.50b + 1.50p ≤ 9
Hope this helped =)