3. James Augustine wants to deposit the following into his savings account: 12 one-dollar bills, 4 five-dollar
bills, 10 quarters, 12 dimes, 40 pennies, a check for $132.51, and a check for $32.12. He wants to receive 2
twenty-dollar bills in cash. How much will he deposit?
( don’t answer with links plz they don’t work for me (: )
Answers
Answer:
James Augustine would have deposited $160.73 into the bank
Step-by-step explanation:
\(12+20+2.50+1.20+0.40+132.51+32.12-40=160.73\)
Related Questions
utomobile trips there are major roads from city to city and major roads from city to city . how many different trips can be made from city to city passing through city ?
Answers
There are 8 different trips that can be made from City X to City Z, passing through City Y.
To find the number of different trips that can be made from City X to City Z, passing through City Y, we can use the multiplication principle of counting.
First, we need to choose one of the 2 major roads from City X to City Y. Then, for each of these roads, there are 4 major roads from City Y to City Z, and we need to choose one of these roads.
By the multiplication principle of counting, the total number of different trips from City X to City Z, passing through City Y, is the product of the number of choices at each stage. Thus, we get:
Number of different trips = Number of roads from City X to City Y x Number of roads from City Y to City Z
= 2 x 4
= 8
This calculation shows how the multiplication principle of counting can be used to find the total number of possible outcomes in a multi-stage process where the number of choices at each stage is known.
To learn more about outcomes click on,
https://brainly.com/question/14796795
#SPJ4
Complete question is:
Automobile Trips. There Are 2 Major Roads From City X To City Y And 4 Major Roads From City Y To City Z. How Many Different trips can be made from City X to City Z, passing through City Y?
Help me plsss plssss plsssssss
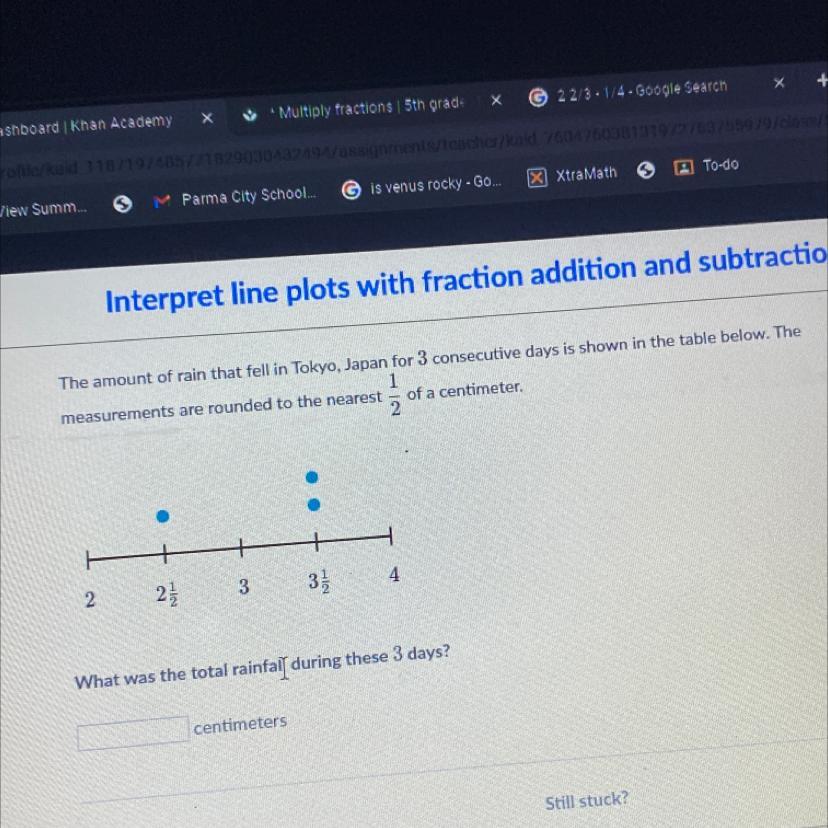
Answers
Answer:
9 1/2
Step-by-step explanation:
Add 2 1/2 plus 3 1/2 plus 3 1/2 to get 9 1/2.
what is the reasoning of 9 +10 is 21?
Answers
Answer:
the reasoning is incorrect.
Step-by-step explanation:
9+10=19.
In triangle ABC, angle A is 35º and angle B is 20°. Select all triangles which are similar totriangle ABC

Answers
To check the simliarity of two triangles only using angles, we can use the correspnding angles criterion. If two pairs of correspondent angles are equal, both triangles are similar.
If two pairs corresponding angles are equal, then the third pair of corresponding angles is equal too.
Just to keep in mind, the sum of the three angles if a triangle is always 180. Then, for trangle ABC, if angle A is 35 and angle B is 20, then, angle C is:
\(\begin{gathered} A+B+C=180^o^{} \\ C=180^o-35^o-20^o \\ C=125^o \end{gathered}\)Angle C is 125°.
Let's check each triangle:
A. Triangel DEF where D is 35° and E is 20° is similar, since corresponding pairs of angles A-D and B-E are congruent.
B. Triangle GHI where G = 35° and I = 30° is NOT similar, since corresponding pair of angles I-C are not congruent (30 and 125). No angle in triangle ABC is 30°.
C. Triangle JKL where J is 35° and L is 125° is similar, corresponding pairs of angles A-J and C-L are congruent (35° and 125°).
D. Triangle MNO with N = 20° and O = 125° is similar, since pairs of corresponding angles B-N and C-O are congruent (20° and 125°)
E. Triangle PQR with Q = 20° and R = 30° is NOT similar, since pair of corre
use a graphing calculator or other technology to answer the question. which quadratic regression equation best fits the data set?
Answers
The quadratic regression equation that best fits the data set is \(y = -1.62x^2 + 34.89x - 5.57.\)
To determine which quadratic regression equation best fits the data set, we can use a graphing calculator or other technology to perform a quadratic regression analysis on the given data.
Using a graphing calculator, we can enter the data set as follows:
Press the STAT button.
Press ENTER to select 1:Edit.
Enter the x-values in L1 and the y-values in L2.
Press STAT again and choose CALC.
Choose option 5:QuadReg.
Press ENTER to select the regression equation.
The calculator will display the quadratic regression equation in the form y = \(ax^2 + bx + c.\)
After performing the quadratic regression analysis, we get the following equation:
y = \(-1.62x^2 + 34.89x - 5.57\)
Therefore, the quadratic regression equation that best fits the data set is \(y = -1.62x^2 + 34.89x - 5.57.\)
Learn more about quadratic regression equation
https://brainly.com/question/30738733
#SPJ4
Full Question: Use a graphing calculator or other technology to answer the question. 4.5 122 Which quadratic regression equation best fits the data set? 6.2 145 7.0 155 8.9 189 O Û = 1.62x2 + 34.89x +5.57 10.1 171 © = -5.5722 + 34.89x – 1.62 14.8 170 O Û = -1.62x2 + 34.89x 15.7 133 © y = -1.62x2 + 34.893 – 5.57

Please I’m giving away Brainly ASAP

Answers
Answer:
g and f are inverse functions because g(f(x)) = f(g(x)) = x
Step-by-step explanation:
Let's start by finding f(g(x)) and g(f(x)). As we discussed in another question, to find a composite function, apply the outer function to whatever the inner function evaluates to. We can start with f(g(x)):
\(f(g(x))=f(\frac{x+6}{7})=7(\frac{x+6}{7} )-6=x+6-6=x\)
Now, let's find g(f(x)):
\(g(f(x))=g(7x-6)=\frac{(7x-6)+6}{7} =\frac{7x}{7}=x\)
There is a property that says that if f(g(x)) = g(f(x)) = x, the two functions are inverse. This suggests that g and f are inverse functions. We can verify this by taking one function, switching y and x, and then solving for y. If we complete this process and find that we get the OTHER function, it means the two functions are inverse. Let's try that:
\(f(x)=y=7x-6\)
Swap x and y:
\(x=7y-6\)
Solve for y:
\(x+6=7y\\y=\frac{x+6}{7}\)
Notice that we got g, which means f and g are inverse.
Instant solution please .
Question 1 B: Solve the following ODE y" + 7y=9e²t,y(0) = 0, and y'(0) = 0
Answers
To solve the following ODE:y" + 7y = 9e² twith initial conditions:y(0) = 0and y'(0) = 0,
We need to follow the steps given below:
Step 1: Characteristic equation For the characteristic equation, we assume the solution of the form:
y = e^(rt)Differentiating it twice, we get:y' = re^(rt)y" = r²e^(rt)
Substituting these in the differential equation, we get:r²e^(rt) + 7e^(rt) = 9e^(2t) => r² + 7 = 9e^t² => r² = 9e^t² - 7
We have two cases to solve:r = ±sqrt(9e^t² - 7)
Step 2: General Solution For each case, the general solution of the differential equation is:
y = c₁e^(sqrt(9e^t² - 7)t) + c₂e^(-sqrt(9e^t² - 7)t)
Step 3: Apply Initial conditions To apply the first initial condition,
we have:y(0) = c₁ + c₂ = 0 => c₂ = -c₁For the second initial condition,
we have:y'(0) = c₁(sqrt(9e^0² - 7)) - c₁(-sqrt(9e^0² - 7)) = 0 => c₁ = 0
Therefore, the solution of the ODE with the given initial conditions is:y = 0
Hence, the solution of the given ODE:y" + 7y = 9e²t, y(0) = 0, and y'(0) = 0 is:y = 0
Note: Since the solution of the differential equation is zero,
it means that the given ODE has no effect on the function and remains constant.
To know more about initial condition visit:
https://brainly.com/question/2005475
#SPJ11
5. What is the range of the function y = 2x – 4?
Answers
Answer:
The domain is how far left and right it goes on a graph, and the range is how far up and down it goes on a graph. Because this equation is linear (if you graphed it, it would be in a straight line), both the domain and range are infinity, because it keeps going up and to the right, the larger X gets, and smaller and to the left, the more negative X gets.
graph is linear:
y=2x-4
solve for x=o
y=2x0-4 Eliminate 0
y=-4 solved for y
solve for y=0
0=2x-4 add 4
+4 +4
4=2x divide by 2
/2 /2
4/2 =x
2=x solved for x
calculate the slope
Solve for x=1
y=2x1-4
y=2-4
y=2 solved for y
Calculating the slope
y -y
a= x=1 x=0 =2
1
The graph is
(0, -4) (2, 0)
Solve the given initial-value problem.
x2y'' + 3xy' = 0, y(1) = 0, y'(1) = 10
Answers
the solution to the initial-value problem is:
y = 10 - 10/x^2.
To solve this second-order linear homogeneous differential equation, we first write it in standard form by dividing both sides by x^2:
y'' + (3/x)y' = 0
This equation is not in the form of a standard linear homogeneous differential equation, so we need to use a substitution to transform it into that form. Let z = y', then we have:
z' + (3/x)z = 0
This is a first-order linear homogeneous differential equation, which we can solve using an integrating factor. The integrating factor is given by:
I(x) = e^(∫(3/x) dx) = x^3
Multiplying both sides of the differential equation by the integrating factor, we get:
x^3 z' + 3x^2 z = 0
This equation can be rewritten as:
d/dx (x^3 z) = 0
Integrating both sides with respect to x, we obtain:
x^3 z = C1
where C1 is an arbitrary constant of integration. Substituting z = y' and solving for y, we get:
y' = C1/x^3
Integrating both sides with respect to x, we obtain:
y = C2 - C1/(2x^2)
where C2 is another arbitrary constant of integration. Using the initial conditions, we have:
y(1) = 0, so C2 - C1/2 = 0, or C2 = C1/2
y'(1) = 10, so C1 = 20
Substituting these values, we have:
C2 = 10
Therefore, the solution to the initial-value problem is:
y = 10 - 10/x^2.
Visit to know more about initial-value problem:-
https://brainly.com/question/31041139
#SPJ11
What is the midpoint to this line segment?

Answers
Answer:
I think 5
Step-by-step explanation:
the inside diameter (in inches) of 50 lightweight snaps used in assembling computer cases are measured and sorted with the following resulting data: 0.0395 0.0443 0.0450 0.0459 0.0470 0.0485 0.0486 0.0487 0.0489 0.0496 0.0499 0.0500 0.0503 0.0504 0.0504 0.0516 0.0529 0.0542 0.0550 0.0571 (a) compute the sample mean and sample variance. (b) find the sample upper and lower quartiles. (c) find the sample median. (d) construct a box plot of the data. (e) find the 5th and 95th percentiles of the inside diameter.
Answers
(a) the sample mean is 0.0494 and the sample variance is 0.000016, (b) the upper quartile is 0.04775, and the lower quartile is 0.0510, (c) the sample median is 0.04975, (d) boxplot is attached, and (e) the 5th and 95th percentiles of the inside diameter are 0.03974 and 0.056995 respectively.
(a) The mean = sum of all values divided by the number of values
μ = (x1 + x2 + ..... + xn)/n
n = 20
μ = (0.0395 + 0.0443+ 0.0450 + ... + 0.0550 + 0.0571)/20
μ = 0.9878/20
μ = 0.0494
(b) Variance = sum of squared deviations from the mean divided by n-1
s² = {(x1-μ)² + (x2-μ)² + .... (xn - μ)²)/(n-1)
s² = {(0.0395-0.0494)² + (0.0443-0.0494)² + .... +(0.0571-0.0494)²}/19
s² = 0.000016
(b) The minimum is 0.0395 and the maximum is 0.0571.
since the number of data is even, the median will be the average of two middle values.
M = Q2 = (0.0496+0.0499)/2 = 0.04975
Now, the first quartile is the median of the data values below the median
so Q1 = (0.0470+0.0485)/2 = 0.04775
And third quartile will be the median of the data values above the median
Q3 = (0.0504+0.0516)/2 = 0.0510
(c) Since we know that the number of data values is even, the median will be the average of the two middle values of the data set
so M = (0.0496+0.0499)/2
or M = 0.04975
(d) The boxplot is at maximum and minimum values. It will start in Q1 and end in Q3 and has a vertical line at the median or Q2.
The boxplot is attached.
(e) The 5th percentile means 0.05(n+1)th data value
or = 0.05(20+1) = 1.05th data value
5th percentile = 0.0550 + 0.05(0.0443-0.0395) = 0.03974
similarly,
95th percentile = 0.0550 + 0.95(0.0571-0.0550) = 0.056995
Therefore, (a) the sample mean is 0.0494 and the sample variance is 0.000016, (b) the upper quartile is 0.04775, and the lower quartile is 0.0510, (c) the sample median is 0.04975, and (e) the 5th and 95th percentiles of the inside diameter are 0.03974 and 0.056995 respectively.
To read more about quartile:
https://brainly.com/question/15642066
#SPJ4

Maya brought some orange slices for her volleyball team to eat between games. They
divided the orange slices equally among the 8 team members, so each team member got
6 orange slices. Lets be the number of orange slices Maya brought. Write and solve an
equation to find s.
Answers
Answer:
48
Step-by-step explanation:
6 times 8=48
Convert the following improper fraction to a mixed number 58/15
Answers
Answer: 3 13/15
Step-by-step explanation:
58/15= 3.8666666666667 = 3
58 - (15 x 3) = 13
3 13/15
-100/-20 multiplying integers
Answers
−100×(−20)=?
2000
Find the tenth term of the sequence 3,2,-1,-6,-13
Answers
Answer:
-78
Step-by-step explanation:
Answer:
to advance from 7th to 21st term of an arithmetic sequence one must add the constant difference 14 times. from 21 to 301 is advancement by 280, in total; thus d = 280/14 = 20. Tenth term is 21 + 3(20) = 81
Step-by-step explanation:
hope this helps
a wall has a perimeter of 120 what is the perimeter of the wall in inches
Answers
The Perimeter of wall in inches is 4.724412 inches.
We have the Perimeter = 120 m
We know 1 m = 39.3701 inch
Then, the perimeter inches
= 39.3701 x 120
= 472.4412 inches
and, 1 cm= 0.393701 inch
Then, perimeter
= 12 x 0.393701
= 4.724412 inches
Learn more about Unit Conversion here:
https://brainly.com/question/19420601
#SPJ1
Anyone help please anyone

Answers
B)when multiplying 6i and 2i he gave it an exponent instead of canceling the i out
C)he never carried the other 12 down so there was no 22
Find the area of the region bounded by \[ y=\frac{7}{(4+x)^{2}}+\frac{5}{7+x^{2}}, \quad y=0, x \geq 5 . \]
Answers
The area of the region bounded by
\[y=\frac{7}{(4+x)^2}+\frac{5}{7+x^2},\ y=0,\ x\ge5\]is 0.0188 (rounded to four decimal places).
Here's how to get the solution:
We are asked to find the area of the region bounded by the two curves.
The curves intersect at (5, 0) because x can not be less than 5.
They meet again at the point x ≈ 1.281.
Now, we must find the integrals for both functions in the given range.
We'll call the first function "f (x)" and the second "g (x)."
f(x) = 7 / (4 + x)² + 5 / (7 + x²)
g(x) = 0
The area between the two curves is obtained by finding the integral of the difference of the two functions.
The area is given by:
\[\int_{5}^{1.281} [f(x) - g(x)] dx\]
Since there is no point of intersection beyond x ≈ 1.281, we will use this value for the limit of integration.
Integrating:
\[\begin{aligned} &\int_{5}^{1.281} [f(x) - g(x)] dx \\ =& \int_{5}^{1.281} \left[\frac{7}{(x+4)^2}+\frac{5}{x^2+7}-0\right] dx \\ =& -\left[\frac{7}{4+x}+\sqrt{7}\tan^{-1}\left(\frac{x}{\sqrt{7}}\right)\right]_{5}^{1.281} \\ =& 0.0188. \end{aligned}\]
Thus, the area of the region is 0.0188.
Learn more about "calculating area by integration":
brainly.com/question/30452445
#SPJ11
At the start of her shift at Midtown Bakery, Megan made some batches of cookies that called for 3 cups of flour each. Then, she used the remaining 8 cups of flour she had to make a pan of muffins. She started her shift with a 20-cup bag of flour.
Answers
Answer:
Step-by-step explanation:
26
Latoya builds a border for her strawberry plot, which is shaped like a square. All the sides measure 5 feet. How many feet of border does she need to buy?
Answers
The amount of feet of border that she needs to purchase is given as follows:
20 feet.
How to obtain the perimeter of a square?The perimeter of a square of side length s is given by the multiplication of four and the side length s, as follows:
P = 4s.
All the sides measure 5 feet, hence the parameter s is given as follows:
s = 5.
Then the perimeter of the square plot is given as follows:
P = 4 x 5
P = 20 feet.
More can be learned about the perimeter of a square at https://brainly.com/question/25092270
#SPJ1
please help me!!!!!!!!

Answers
Answer:
see explanation
Step-by-step explanation:
Using the double angle identity for cosine
cos2x = 2cos²x - 1
Given
cos( \(\frac{0}{2}\) ) = \(\frac{1}{2}\)( p + \(\frac{1}{p}\) ) , then
cosΘ = 2[ \(\frac{1}{2}\)(p + \(\frac{1}{p}\) ) ]² - 1
= 2 [ \(\frac{1}{4}\)(p² + 2 + \(\frac{1}{p^{2} }\) ) ] - 1 ← distribute by 2
= \(\frac{1}{2}\)(p² + 2 + \(\frac{1}{p^{2} }\) ) - 1 ← distribute by \(\frac{1}{2}\)
= \(\frac{1}{2}\) p² + 1 + \(\frac{1}{2p^2}\) - 1
= \(\frac{1}{2}\) p² + \(\frac{1}{2p^2}\) ← factor out \(\frac{1}{2}\) from each term
= \(\frac{1}{2}\) ( p² + \(\frac{1}{p^{2} }\) ) ← as required
Answer:
Step-by-step explanation:
Hello, please consider the following.
\(cos(\theta)=2cos^2(\dfrac{\theta}{2})-1\\\\=2\left(\dfrac{p+\dfrac{1}{p}}{2}\right)^2-1\\\\=\dfrac{p^2+\dfrac{1}{p^2}+2}{2}-1\\\\=\dfrac{1}{2}(p^2+\dfrac{1}{p^2})+1-1\\\\=\dfrac{1}{2}(p^2+\dfrac{1}{p^2})\)
Thank you
help im in k12 9th grade
Factor
x2+7x+10
Question 2 options:
(x+1)(x+10)
(x+3)(x+4)
(x−2)(x−5)
(x+2)(x+5)
Answers
When factoring find 2 numbers that when added together equal the middle value and when multiplied equal the last value.
min this problem the middle value is 7 and the last value is 10
5 + 2 = 7 and 5 x 2 = 10
The answer is: (x+2)(x+5)
Answer:
(x+2)(x+5)Step-by-step explanation:
Factoring x^2+7x+10 The first term is, x^2 its coefficient is 1 .The middle term is, +7x its coefficient is 7 .The last term, "the constant", is +10 Step-1 : Multiply the coefficient of the first term by the constant 1 * 10 = 10 Step-2 : Find two factors of 10 whose sum equals the coefficient of the middle term, which is 7 . -10 + -1 = -11 -5 + -2 = -7 -2 + -5 = -7 -1 + -10 = -11 1 + 10 = 11 2 + 5 = 7 That's itStep-3 : Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, 2 and 5 x2 + 2x + 5x + 10Step-4 : Add up the first 2 terms, pulling out like factors : x * (x+2) Add up the last 2 terms, pulling out common factors : 5 * (x+2)Step-5 : Add up the four terms of step 4 : (x+5) * (x+2) Which is the desired factorizationSolution:
(x+2) * (x+5)find the largest number such that if |x − 4| < , then |2x − 8| < , where = 0.5.
Answers
The largest number that satisfies both inequalities is x = 4.
We want to find the largest number x such that if |x - 4| < 0.5, then |2x - 8| < 1.
First, consider the inequality |x - 4| < 0.5. This means that x is within 0.5 units of 4, or:
3.5 < x < 4.5
Next, consider the inequality |2x - 8| < 1. This means that 2x - 8 is within 1 unit of 0, or:
-1 < 2x - 8 < 1
Adding 8 to all parts of the inequality gives:
7 < 2x < 9
Dividing by 2 gives:
3.5 < x < 4.5
Notice that this is the same interval as the first inequality. Therefore, the largest number that satisfies both inequalities is x = 4.
So, if |x - 4| < 0.5, then |2x - 8| < 1 is satisfied for x = 4.
To know more about inequality here
https://brainly.com/question/30228778
#SPJ4
if rose and Carl share a 18 ounce bucket of clay. by the end of the week rose has used 1/6 of the Bucket and carl used 2/3 of the bucket How many ounces are left in the bucket
Answers
Answer:
3 ounces left
Step-by-step explanation:
We convert both 2/3 and 1/6 into a similar fraction. In this case, the simplest way to answer the problem is to convert them into eighteenths, as when we convert them to this, the numberator will show the amount of ounces used. SO, 2/3=12/18=12 ounces used and 1/6=3/18=3 ounces used. The total answer of ounces used is 15, so 18-15=3 ounces left
Which of the following is true of programmed decisions?
(A) They are new and complex decisions.
(B) They require creative solutions.
(C) They have an established decision rule.
(D) They require detailed judgement.
Answers
The true statement regarding programmed decisions is option(C) They have an established decision rule.
Programmed decisions are repetitive and routine in nature, involving situations that have occurred before and for which there are established guidelines or rules to follow. These decisions can be automated and do not require extensive analysis or subjective judgment. They are typically based on standard operating procedures, policies, or predefined algorithms that guide the decision-making process. The established decision rule allows for consistent and efficient decision-making in repetitive situations, saving time and effort.
Programmed decisions are often applied in structured environments where the decision-making process can be clearly defined and standardized. In contrast, new and complex decisions (A) usually require a more dynamic and flexible approach, creative solutions (B), and detailed judgment (D) as they involve unfamiliar situations that lack established rules or precedents.
To know more about programmed decisions, refer here:
https://brainly.com/question/13631418#
#SPJ11
two narrow slits 70 μm apart are illuminated with light of wavelength 550 nm . part a what is the angle of the m = 3 bright fringe in radians?
Answers
The angle of the m=3 bright fringe in radians can be calculated using the formula θ = sin^(-1)(mλ/d), where θ is the angle, λ is the wavelength of light, d is the distance between the slits, and m is the order of the bright fringe.
Substituting the values given, we get θ = sin^(-1)((3)(550 nm)/(70 μm)).
First, we need to convert the wavelength to the same unit as the distance between the slits, which is 0.55 μm. Then we can convert the result to radians by dividing by 180/π.
The final answer is θ = 0.063 radians (rounded to three decimal places). This means that the m=3 bright fringe is located at an angle of approximately 3.61 degrees with respect to the central maximum.
This calculation is an example of the interference of light waves through a double-slit experiment, which demonstrates the wave nature of light.
Learn more about angle here:
https://brainly.com/question/28451077
#SPJ11
Solve inequality and graph solution 3>4x-1
Answers
Answer: x < 1
--------------------
find the area and circumference of the 2 circles

Answers
Answer:
32, 45
Step-by-step explanation:
Given: QR ≈ ST, PQ ≈ PT
Prove: ΔPQR ≈ ΔPTS
Answers
ΔPQR is similar to ΔPTS by the Side-Angle-Side similarity criterion.
To prove that triangles PQR and PTS are similar, we need to show that their corresponding angles are congruent and their corresponding sides are proportional.
Given:
1. QR ≈ ST (Segment similarity)
2. PQ ≈ PT (Segment similarity)
To prove:
ΔPQR ≈ ΔPTS
Proof:
1. We know that if two sides of a triangle are proportional to two sides of another triangle, and their included angles are congruent, then the triangles are similar (Side-Angle-Side similarity).
2. From statement 1, we have QR ≈ ST. This implies that the sides QR and ST are proportional.
3. From statement 2, we have PQ ≈ PT. This implies that the sides PQ and PT are proportional.
4. We also know that corresponding angles of similar triangles are congruent.
5. Let's examine the corresponding angles of the two triangles:
- ∠Q in ΔPQR corresponds to ∠T in ΔPTS.
- ∠P in ΔPQR corresponds to ∠P in ΔPTS.
- ∠R in ΔPQR corresponds to ∠S in ΔPTS.
6. Therefore, we have corresponding angles ∠Q ≅ ∠T, ∠P ≅ ∠P, and ∠R ≅ ∠S.
7. Based on the side and angle relationships established in steps 2 and 6, we can conclude that ΔPQR ≈ ΔPTS by the Side-Angle-Side similarity criterion.
Thus, we have proven that triangles PQR and PTS are similar.
Learn more about similarity here: https://brainly.com/question/29731302
#SPJ11
Compare the budgets of Hong Kong, United States of America, and
Korea based on your definition of a budget, in terms of contents,
formats, advantages, and disadvantages, etc.
Answers
The budgets of Hong Kong, the United States of America, and Korea differ in contents, formats, advantages, and disadvantages. While each budget has its strengths and weaknesses, they all aim to provide a clear and transparent financial plan for their respective countries.
A budget is a financial plan that estimates expected income and expenditure for a specific period. It may include income, expenses, debts, and savings. Budgets may vary from country to country and can be analyzed by comparing their contents, formats, advantages, and disadvantages. Here are the budgets of Hong Kong, the United States of America, and Korea:
Hong Kong Budget:Contents: The Hong Kong budget comprises revenue and expenditure. It provides a detailed analysis of expected sources of income and the allocation of funds.Format: The Hong Kong budget is presented in a clear and concise format, including charts and graphs to aid understanding.Advantages: The budget is easy to understand, and it promotes transparency and accountability.Disadvantages: It does not provide detailed information on tax expenditures and lacks public participation in the budget process.
United States Budget:
Contents: The US budget comprises revenue, expenditures, and deficit or surplus. It includes an analysis of taxes, social security, and Medicare.Format: The US budget is presented in a complex and lengthy format, including tables, graphs, and other financial documents.Advantages: The budget provides detailed information on tax expenditures and encourages public participation in the budget process.Disadvantages: The budget can be challenging to understand due to its complexity, and it may not provide an accurate depiction of federal spending.Korean Budget:
Contents: The Korean budget comprises revenue, expenditures, and surplus or deficit. It includes detailed information on taxes, social security, and public welfare.Format: The Korean budget is presented in a clear and concise format, including tables and charts to aid understanding.Advantages: The budget is easy to understand, and it promotes transparency and accountability. It also provides detailed information on social welfare expenditures.Disadvantages: The budget may not provide an accurate depiction of government spending, and it may not include information on hidden expenditures.Learn more about Budget:
https://brainly.com/question/26894404
#SPJ11