Answers
Answer:
Step-by-step explanation:
r(x)= (x-3)(x+5)
= x²+5x-3x-15
=x²+2x-15
Answer:
\({\huge{\pink{\underline{\underline{QuEsTiOn}}}}}\)
rewrite r(x) in expanded form
\({\huge{\pink{\underline{\underline{SoLuTiOn}}}}}\)
\((x-3)(x+5)\\
=>x(x + 5) - 3(x + 5) \\
= > {x}^{2} + 5x - 3x + 15\\
=> {x}^{2} + 2x + 15 \)
Related Questions
(q1) Find the length of the curve described by the function

Answers
The value of the Integral at the lower limit from the value of the integral at the upper limit to get the length of the curve.
The length of the curve described by the function f(x) = 1 + 3x^2 + 2x^3 is to be found. The formula used to find the length of a curve is:
L = ∫(sqrt(1 + [f'(x)]^2))dx where f'(x) is the derivative of f(x)We have to first find f'(x):f(x) = 1 + 3x^2 + 2x^3f'(x) = 6x + 6x^2
The integral becomes:L = ∫(sqrt(1 + [6x + 6x^2]^2))dx = ∫(sqrt(1 + 36x^2 + 72x^3 + 36x^4))dx The integral appears to be difficult to evaluate by hand.
Therefore, we use software like Mathematica or Wolfram Alpha to solve the problem. Integrating the expression using Wolfram Alpha gives:
L = 1/54(9sqrt(10)arcsinh(3xsqrt(2/5)) + 2sqrt(5)(2x^2 + 3x)sqrt(9x^2 + 4))The limits of integration are not given. Therefore, the definite integral be solved.
We can, however, find a general solution. We use the above formula and substitute the limits of integration.
Then, we subtract the value of the integral at the lower limit from the value of the integral at the upper limit to get the length of the curve.
To know more about Integral.
https://brainly.com/question/27419605
#SPJ8
The value of V-4 is not -2 because .
A.
(-2)2 -4
B.
22 -4
C.
(-4)2 -2
D.
42 -2

Answers
9514 1404 393
Answer:
A
Step-by-step explanation:
The correct choice is marked.
The square of the square root is the number being rooted. -2 is not the square root of -4 because it square (-2)² is a positive number, not equal to -4.
Makesha lost 58.5 pounds in 18 weeks. Find her rate of loss in pounds per week.
Answers
If an investment company pays 6% compounded semiannually, how much will you have 5 years from now if you deposit $900?
How much would you earn if it were simple interest instead of compound interest?
Answers
With compound interest of 6% paid semiannually, a deposit of $900 would result in $1,191.02 after 5 years, while simple interest would earn $270, resulting in a total of $1,170.
To calculate the future value of an investment with compound interest, we can use the following formula:
FV =\(PV * (1 + r/n)^{(n*t)}\)
where FV, PV, r, n and t is the future value, present value, annual interest rate, number of compounding periods per year and number of years respectively.
In this case, the present value (PV) is $900, the annual interest rate (r) is 6%, and the interest is compounded semiannually, so there are 2 compounding periods per year (n=2). The period (t) of investment is 5 years.
Using these values, we can calculate the future value (FV) as follows:
FV = \(\$900 * (1 + 0.06/2)^{(2*5)\)
= \(\$900 * (1.03)^{10\)
= $1,191.02
Therefore, the future value of the investment after 5 years with compound interest would be $1,191.02.
If the interest were simple interest instead of compound interest, the calculation would be simpler. Simple interest is calculated as follows:
I = P x r x t
where I is the interest, P is the principal or present value, r is the interest rate, and t is the time period.
In this case, the interest rate is still 6% and the investment period is still 5 years, but the interest is calculated only on the principal amount of $900. Therefore, the interest earned would be:
I = $900 x 0.06 x 5
= $270
Therefore, the total amount after 5 years with simple interest would be the sum of the principal and the interest earned, which is:
Total = $900 + $270
= $1,170
Therefore, if the interest were simple interest instead of compound interest, the total amount after 5 years would be $1,170, and the interest earned would be $270.
Leaen more about simple interest here:
https://brainly.com/question/30824126
#SPJ1
please i’ll fail if i don’t get this right. please i’ll give brainlyist The current temperature of 15°F below zero is 18°F below the high temperature of the day. What is the high temperature for the
day?
OA. 5°F
ов. 33°F
OC. 3°F
OD. 33°F
Answers
Answer:
I think its C
Step-by-step explanation:
What equation is equivalent to 6x + 13 - (3x - 7)
Answers
Answer:
6x + 12 - (3x - 7)
6x + 12 - 3x + 7
3x + 19
Step-by-step explanation:
Simplifying
6x + 13 + -3x + -7 = 0
Reorder the terms:
13 + -7 + 6x + -3x = 0
Combine like terms: 13 + -7 = 6
6 + 6x + -3x = 0
Combine like terms: 6x + -3x = 3x
6 + 3x = 0
Solving
6 + 3x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-6' to each side of the equation.
6 + -6 + 3x = 0 + -6
Combine like terms: 6 + -6 = 0
0 + 3x = 0 + -6
3x = 0 + -6
Combine like terms: 0 + -6 = -6
3x = -6
Divide each side by '3'.
x = -2
Simplifying
x = -2
Use a geometric tool to draw a circle. Draw and measure a radius and a diameter of the circle .
Answers
Answer:
Attached is an example of a circle with a radius of 5 and a diameter of 10.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

the tables represent two linear functions in a system. what is the solution to this system?

Answers
Answer: The solution is the point (-14, -54)
Step-by-step explanation:
When we have a system of linear equations like:
y = a*x + b
y = c*x + d
The solution of this system is the point (x, y) that is a solution for both equations, if we graph the lines, this point would be the point where the lines intersect.
To start with this, we need to find the equations of the lines, we will use the following:
A linear relationship can be written as:
y = a*x + b
where a is the slope and b is the y-axis intercept.
For a line that passes through the points (x1, y1) and (x2, y2), the slope can be written as:
a = (y2 - y1)/(x2 - x1).
Now, for the first table, we can use the points: (-3, -10) and (0, 2)
The slope of this line is:
a = (2 - (-10))/(0 - (-3)) = 12/3 = 4
then we have:
y = 4*x + b
To find the value of b, we can just replace one of the points in the equation, for example, we can use the point (0, 2), this means that we need to replace x by 0, and y by 2.
2 = 4*0 + b
2 = b
Then the equation for the first table is y = 4*x + 2
For the second table, we can use the points (0, -12) and (3, - 3)
Then the slope is:
a = (-3 - (-12))/(3 - 0) = 9/3 = 3
Then we have:
y = 3*x + c
And to find the value of c, we can do the same as before, now we use the point (0, -12) then:
-12 = 3*0 + c
-12 = c
Then the equation for this line is:
y = 3*x - 12
The system of linear equations is then:
y = 4*x + 2
y = 3*x - 12
To find the solution of the system, we must have that y = y, then we can write:
4*x + 2 = y = 3*x - 12
4*x + 2 = 3*x - 12
Now we can solve this for x.
4*x - 3*x = -12 - 2
x = -14
x = -14
Now we can replace this in one of the equations to find the value of y.
y = 3*(-14) - 12 = -54
Then the solution is the point (-14, -54)
Find the mean absolute deviation (MAD) of the data in the pictograph below.

Answers
Answer:
its 1
Step-by-step explanation:
Correct answer gets brainliest!!!!

Answers
Answer:
A is incorrect because points are: (length [x], height [y])
B is correct because a point is not a size, it is a position, and they have no dimensions, as they are a dot.
C is incorrect, as I explained above.
D is incorrect, also as I explained above.
Select the bolded answers, as the question asks which are false
Imma get that brainliest ;)
Answer:
It's has to be D) because it says it depends on their dimensions.
Step-by-step explanation:
a) says they have no length or high which is almost the same thing as B).
Cuz B) they have no size or dimension
which that means that if you have to check if they all apply they all have to be the same thing in different words.
C) says their size variety which variety means it could be different types it could be without dimension it could be tall or etc
And D) says their size depends on their dimension all the others say don't have size or dimension. I hope this helps you
The image of triangle ABC after a 180° rotation around
the origin is:
A'(-1, 2)
B'(-4, 2)
C'
Answers
Answer:If A is at point (x,y), then A' would be at point (-x,-y). Same goes for points B and C.
Step-by-step explanation:
please help!! 100 points

Answers
Explanation:
Plug in 4 for x
H(4)=1/5(4^2-6)-8
After solving you should get -6
\(\\ \tt\bull\rightarrowtail h(x)=1/5(x^2-6)-8\)
\(\\ \tt\bull\rightarrowtail h(4)\)
\(\\ \tt\bull\rightarrowtail 1/5(4^2-6)-8\)
\(\\ \tt\bull\rightarrowtail 1/5(16-6)-8\)
\(\\ \tt\bull\rightarrowtail 10/5-8\)
\(\\ \tt\bull\rightarrowtail 2-8\)
\(\\ \tt\bull\rightarrowtail -6\)
Simplify 3(x+2) + 2x + 5
Answers
Answer:
\(5x+11\)
Step-by-step explanation:
Step 1: Distribute
\(3x+6+2x+5\)
Step 2: Add like terms
\(5x+11\) < your answer
-3x-5x+8=16
Please I don’t understand
Answers
-1
We can solve in this way,
-3x-5x+8=16
-8x=16-8
-8x=8
x= -8/8
x= -1
Therefore for this equation, x= -1.
Answer is -1
Solve the following compound inequality
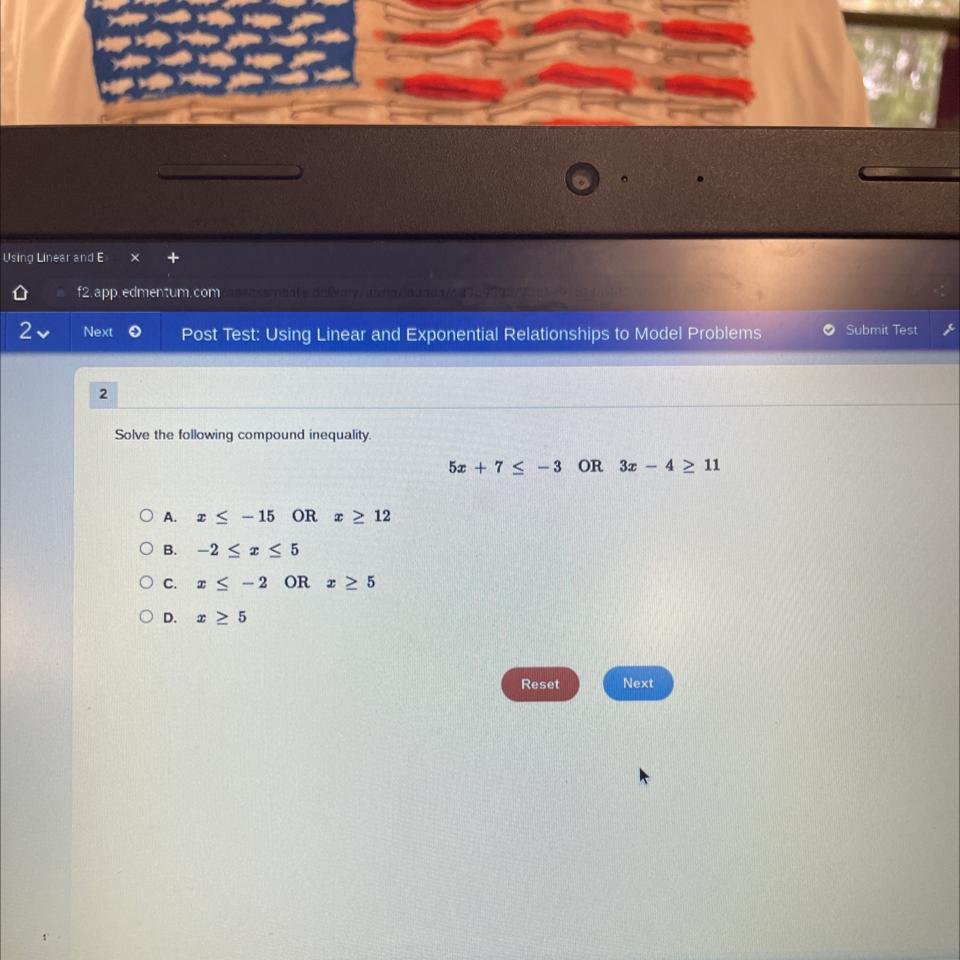
Answers
The solution of the compound inequality 5x + 7 ≤ - 3 or 3x - 4 ≥ 11 is x ≤ -2 or x ≥ 5. Therefore, the answer is C.
How to solve compound inequalities?An inequality is an expression containing <, >, ≤ and ≥.
A compound inequality is an inequality that combines two simple inequalities.
Therefore, let's solve the compound inequality as follows:
5x + 7 ≤ - 3 or 3x - 4 ≥ 11
5x + 7 ≤ - 3
5x ≤ -3 - 7
5x ≤ - 10
divide both sides by 5
x ≤ - 10 / 5
x ≤ -2
3x - 4 ≥ 11
3x ≥ 11 + 4
3x ≥ 15
x ≥ 15 / 3
x ≥ 5
Therefore,
x ≤ -2 or x ≥ 5
learn more on inequality here: https://brainly.com/question/28600203
#SPJ1
The owner of a restaurant is concerned about customers who ask for a water cup when placing an order but fill the cup with a drink from the beverage fountain instead of filling the cup with water. The owner randomly selected 90 people who order a water cup and found that 21 of those customers filled the cup with a soft drink.a. Construct and interpret a 95 percent confidence interval for the proportion of all customers who, having asked for a water cup when placing an order, will fill the cup with a soft drink from the beverage fountain. b. The owner estimates that each customer who asks for a water cup but fills it with a soft drink costs the restaurant $0.35. Suppose that in the month of June 2,500 customers ask for a water cup when placing an order. Use the confidence interval constructed in part (a) to give an interval estimate for the cost to the restaurant for the month of June from the customers who ask for a water cup but fill the cup with a soft drink.
Answers
Answer:
This is very confusing.
Can you try and make this a shorter question for me to answer?
Step-by-step explanation:
Matt is helping to set up drinks and snacks for a luncheon.
Matt has 4.8 liters of iced tea. He is going to pour this into pitchers that can each only hold 0.8 liters of iced tea.
If Matt pours an equal amount of iced tea into each pitcher, how many pitchers does he fill?
Answers
Answer:
he will fill 6 pitchers
Step-by-step explanation:
4.8÷0.8=6
Goldie Gold Jewelry uses direct labor hours to apply overhead and estimated total overhead costs at $52,500 and direct labor hours at 12,500 for the second quarter. The direct labor quantity standard is 1.75 direct labor hours per unit, and the company produced 5,250 units in the second month of the second quarter. This required 2,625 direct labor hours. What was the overhead rate for the second quarter?
Answers
In the case above, the value of the overhead rate for the second quarter is $17,640.
What is the overhead rate about?Note that:
In the case above, for one to be able to calculate the predetermined overhead rate, a person need to divide the value of the estimated overhead costs which is $52,500 by that of the estimated direct labor hours .
Predetermined overhead rate=Estimated overhead costs/ estimated direct labor hours
Predetermined overhead rate=$52,500/ 12,500
Predetermined overhead rate=$4.20/DLH overhead rate
Hence: $52,500/ 12,500 = $4.20/DLH overhead rate.
Since the Overhead that was applied at standard hours was said to be allowed, then:
= $4.2 x 2,400 x 1.75
= $17,640.
Therefore, In the case above, the value of the overhead rate for the second quarter is $17,640.
Learn more about overhead rate from
https://brainly.com/question/16256360
#SPJ1
X+10=3(x-1)^2 written in standard form
Answers
Answer:
3x^2-7x-7
Step-by-step explanation:
(x-1)^2= x^2-2x+1
x+10 = 3(x^2-2x+1)
x+10 = 3x^2-6x+3
Then subtract x+10 from both sides which equals:
3x^2-7x-7
Two buildings are 18 m part. The shorter building is 12 m high while the taller one is 19 m high. Find the distance, x m between the top of the buildings.
Answers
The distance between the tops of the buildings is 28.5 meters.
To find the distance between the top of the buildings, we can use the concept of similar triangles.
Let's denote the height of the shorter building as "a" (12 m) and the height of the taller building as "b" (19 m). The distance between the buildings can be denoted as "c" (18 m), and the distance between the top of the buildings as "x" (which we need to find).
We can set up a proportion based on the similar triangles formed by the buildings:
a/c = b/x
Substituting the known values:
12/18 = 19/x
To find "x," we can cross-multiply and solve for "x":
12x = 18 * 19
12x = 342
x = 342/12
x = 28.5 m
Therefore, the distance between the tops of the buildings is 28.5 meters.
for such more question on distance
https://brainly.com/question/12356021
#SPJ8
72=2+5(-2–4x)
-4
4
-20
20
No solution
Answers
Answer:
-4
Solution:
72 = 2 + 5(-2 - 4x)
Distribute right side
72 = 2 - 10 - 20x
Combine like terms
72 = -8 - 20x
Add 8 to both sides
80 = -20x
Divide -20 to both sides
-4 = x
Best of Luck!
Nina and Luca were told to draw a net for the three-dimensional figure shown below. Which statement
nets is true?
Three-dimensional Figure
Answers
Answer:
d
Step-by-step explanation:

The perimeter of the figure below is 35. Find
the missing value.

Answers
Answer: 7 feet
Step 1: Add the values of the sides we know the length of.
9 + 9 + 10 = 28.
Step 2: Subtract the number 28 from 35.
35 - 28 = 7
The answer is 7. Hope this helps!
Answer:
35 - 28 = 7
Step-by-step explanation:
7
Thanks bro...
Find the area of square that has the same perimeter as a rectangle whose length and breadth are 18cm and 8cm respectively
Answers
Answer:
169
Step-by-step explanation:
The perimeter of the square and rectangle are said to be the same. Therefore we have to find the perimeter which is :Perimeter of a rectangle= 2(length+breath)
2(18 + 8)
2(26)
52.
A square has four equal sides.
The length will be determined by dividing 52 by 4
\(52 \div 4 = 13\)
The length is 13.
Since the area of a square is
\( {l}^{2} = {13}^{2} \)
L is length.
The answer is
\( {169}^{2} \)
C=5/9 (F - 32), for F
Answers
Answer: f=32+9/5c,c=r
Step-by-step explanation:
Compare the functions shown below:
g(x)
X
O f(x)
O g(x)
-16
01
f(x) = 4 sin (2x-1)-11 -2 h(x)=(x-2)² +4
2 -3
3-2
1
4
5
6
Which function has the smallest minimum y-value? (2 points)

Answers
Answer:
Step-by-step explanation:
To compare the minimum y-values of the given functions, we need to find the minimum point of each function and compare their respective y-values.
For the function f(x) = 4 sin(2x-1) - 11, we know that the sine function oscillates between -1 and 1, and is multiplied by a factor of 4, which will change the amplitude of the function. We can find the minimum point of the function by setting its derivative equal to zero:
f'(x) = 8 cos(2x-1) = 0
cos(2x-1) = 0
2x-1 = (2n+1/2)π, where n is an integer
x = (2n+1/4)π + 1/2, where n is an integer
The minimum point will occur at x = (2n+1/4)π + 1/2, and the corresponding y-value can be found by substituting this value of x into the original function:
f(x) = 4 sin(2x-1) - 11
f((2n+1/4)π + 1/2) = 4 sin(2[(2n+1/4)π + 1/2]-1) - 11
f((2n+1/4)π + 1/2) = 4 sin(2nπ + π/2) - 11
f((2n+1/4)π + 1/2) = 4 (-1)^n - 11
We can see that the y-value of the minimum point alternates between -15 and -7 as n changes. Therefore, the smallest minimum y-value for the function f(x) is -15.
For the function h(x) = (x-2)² + 4, we know that it is a quadratic function with a minimum point at x=2. The y-value of the minimum point can be found by substituting x=2 into the function:
h(2) = (2-2)² + 4
h(2) = 4
Therefore, the smallest minimum y-value among the two given functions is 4, which is the minimum y-value of the function h(x) = (x-2)² + 4.
What is the measure of m?5m15nmm = [ ?]Give your answer in simplest form.Enter
![What is the measure of m?5m15nmm = [ ?]Give your answer in simplest form.Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/HyNOc6r8bqDcOpnYqCMkPeJtjAt4qZu6.jpeg)
Answers
The labelled diagram of the triangle is shown below
From the diagram,
BC is common to triangles ABC and BCD.
AC is the hypotenuse of triangle ABC and BC is the hypotenuse of triangle BCD. CD and BC are corresponding legs of triangles ABC and BCD
Thus,
CD/BC = BC/AC
5/m = m/(15 + 5)
5/m = m/20
By crossmultiplying,
m * m = 5 * 20
m^2 = 100
m = square root of 100
m = 10
![What is the measure of m?5m15nmm = [ ?]Give your answer in simplest form.Enter](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Zx3fvzkh6QAKhJuSvBQM9IeI0p7w2zqS.png)
Given the following table of values for the function f(x), determine f^-1(4)

Answers
Using the inverse of the function from the table, the value of f⁻¹(4) is 107/3
What is the inverse of a function?The inverse of a function is a new function that "undoes" the original function. It reverses the mapping of inputs and outputs, allowing you to find the original input value when you know the output value.
In this problem, we have to use the table to find the original function which is f(x) and use it to find the inverse of the function;
Taking two points from the table;
m = y₂ - y₁ / x₂ - x₁
m = 0 - (-3) / -9 - (-11)
m = 3 / 20
Using the slope and one point on the table;
y = mx + x
-3 = 3/20(-11) + c
-3 = -1.65 + c
c = -3 + 1.65
c = -1.35
Putting the slope and y - intercept together;
y = 3/20x - 1.35
y = 3/20x - 27/20
f(x) = 3/20x - 27/20
Taking the inverse of the function;
f⁻¹(x) = (20x + 27)/3
To find the value of f⁻¹(4), we just need to substituting the value of x in the function;
f⁻¹(4) = (20(4) + 27)/3
f⁻¹(4) = 107/3
Learn more on inverse of a function here;
https://brainly.com/question/3831584
#SPJ1
An amusement park has 20 rides. Ethan has enough time to ride 3 rides before the park closes. How many different ways could Ethan pick to ride the 3 rides?
Answers
Answer
20*19*18 = 6840
UNLESS...............
he is allowed to ride the same ride again , over and over....
then it is 20 x 20 x 20 = 8000
The average monthly income of three persons is rs. 3,600. If the income of the first is 1/5 of the combined income of the other two then his monthly income is
Answers
The monthly income of the first person is $600.
Given that, the average monthly income of three persons is RS 3,600.
The income of the first is 1/5 of the combined income of the other two.
Here, Let income of the first be A, let income of the second be B and let Income of the third be C.
A+B+C=3600 -----(i)
Income for the first person = 1/5(B+C) -----(ii)
Substitute equation (ii) in equation (i), we get
(B+C)/5 +B+C =3600
B+C+5B+5C=3600×5
6B+6C=18000
6(B+C)=18000
B+C=3000 ------(iii)
Substitute (iii) in equation (i), we get
A=$600
Therefore, the monthly income of the first person is $600.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ1
