- 3/4f = 5/4
f = ??
find f
Answers
Answer:
the answer to that, f= -5/3
Related Questions
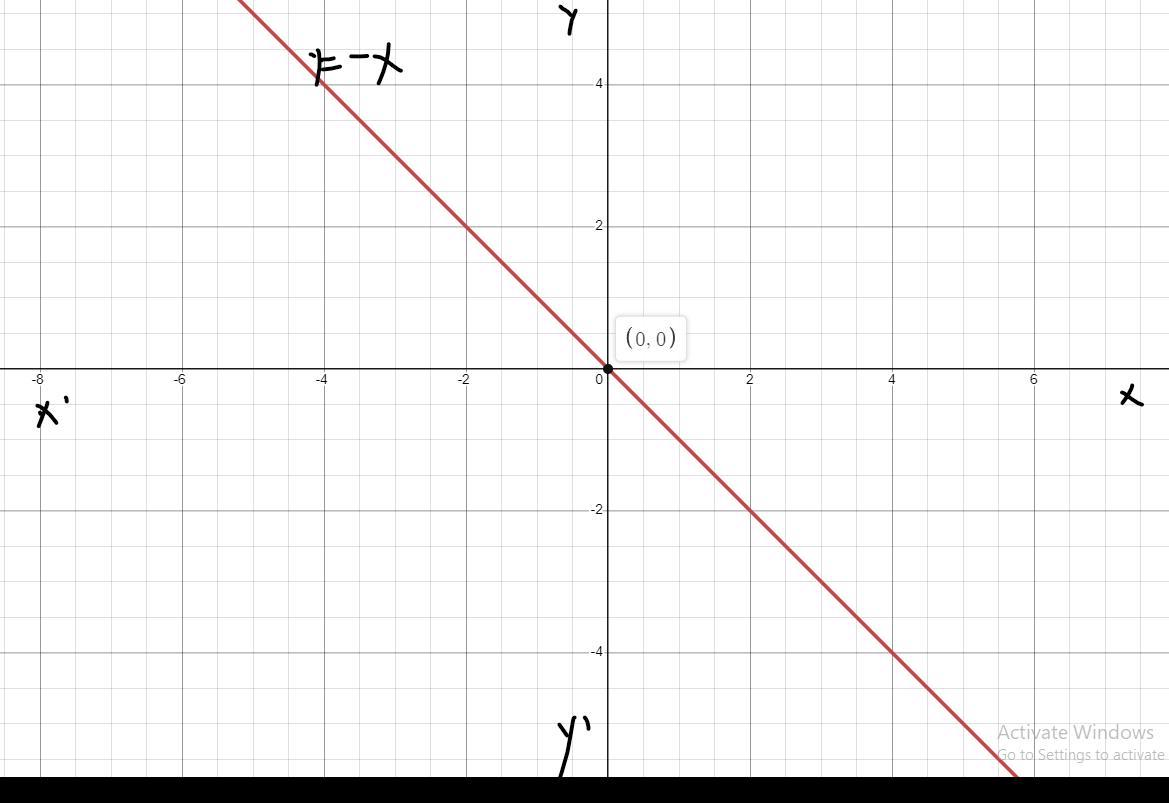
graph the linear function identify the x-intercept.
y=-x
Answers
The x-intercept of the given linear function is 0 and the graph of the linear ufnction is shown.
What is the x-intercept?A line's x-intercept and y-intercept are the points at which the x- and y-axes, respectively, are crossed.We set y = 0 and solve the equation for x to determine the x-intercept. This is due to the fact that the line crosses the x-axis at y=0. If an equation is not in the form y = MX + b, we can still solve for the intercepts by substituting 0 where necessary and then solving for the final variable.So, plot the linear function:
Plot y = -x as follows:(Refer to the graph attached below)
We can clearly see that the x-intercept is 0.Therefore, the x-intercept of the given linear function is 0 and the graph of the linear ufnction is shown.
Know more about the x-intercept here:
https://brainly.com/question/17932786
#SPJ1
14. Which equation can be used to find the
value of x?
(4x-10)
58
A) (4x-10) +58=180
B) (4x-10)-58=180
C) (4x-10) =180
D) (4x-10) =58
Answers
Answer:
(4x - 10) = 58
Step-by-step explanation:
Problem? ? If (4x - 10) - 58 = 0
(4x -10) - 58 +58 = 0 + 58 Add 58 to both side of the equation
(4x - 10) = 58
0.14+0.14+0.14_________0.14×3equal togreater thanless than
Answers
If we compute the operations in each side, we can see that on the left side 0.14+0.14+0.14 is the same as 3 times 0.14, so 3 x 0.14
This means that the expressions are equal to each other:
\(0.14+0.14+0.14=3\times0.14\)Suppose 4
?
Please help I dont understand how to solve it.

Answers
Let's find the smallest number in the range.
Subtract the largest b from the smallest a: 4 - 4 = 0
Then find the largest number in the range.
Subtract the smallest b from the largest a: 5 - 2 = 3
So...
0 < a - b < 3
If a is an integer then there is no value of a as there is no integer present which is greater than 4 and less than 5.
So if a is real.
b can be 3 onlySo
set of values
[1,2]during an experiment, some water was removed from each of 6 water tanks. if the standard deviation of the volumes of water in the tanks at the beginning of the experiment was 10 gallons, what was the standard deviation of the volumes of water in the tanks at the end of the experiment?
Answers
The standard deviation of the volumes of water in the tanks at the end of the experiment is 0.8944.
In this experiment, we are given that the standard deviation of the volumes of water in the tanks at the beginning of the experiment was 10 gallons. This means that the volumes of water in the tanks were spread out around the mean volume, with most of the data falling within 10 gallons of the mean.
During the experiment, some water was removed from each of the 6 tanks. This means that the volumes of water in the tanks have changed and we need to find the new standard deviation of the volumes of water in the tanks.
To find the new standard deviation, we need to use the formula for the sample standard deviation, which is:
s = √[ Σ ( xi - x )² / ( n - 1 ) ]
Where s is the sample standard deviation, xi is each data point, x is the sample mean, and n is the sample size.
s = √[ Σ ( 5 - 3 )² / ( 6 - 1 ) ] = 0.8944
To know more about standard deviation here
https://brainly.com/question/16555520
#SPJ4
find an equation of the plane. the plane through the points (2, −1, 3), (5, 4, 6), and (−3, −3, −3)
Answers
The equation of the plane passing through the points (2, -1, 3), (5, 4, 6), and (-3, -3, -3) is 4x - 4y - 3z - 3 = 0.
To find the equation of the plane passing through the points (2, -1, 3), (5, 4, 6), and (-3, -3, -3), we can use the point-normal form of the equation of a plane. This form uses a point on the plane and the normal vector to define the plane's equation.
First, we need to find the normal vector of the plane. The normal vector is perpendicular to the plane and can be determined using the cross product of two vectors in the plane.
Let's define two vectors in the plane:
Vector A = (5, 4, 6) - (2, -1, 3) = (3, 5, 3)
Vector B = (-3, -3, -3) - (2, -1, 3) = (-5, -2, -6)
Next, we calculate the cross product of vectors A and B:
Normal vector N = A x B = (3, 5, 3) x (-5, -2, -6)
To find the cross product, we can use the determinant of a 3x3 matrix:
N = (5 * (-6) - (-2) * (-3), -[(3 * (-6) - (-2) * 3), 3 * (-2) - 5 * (-5)])
Simplifying, we get:
N = (12, -12, -9)
Now that we have the normal vector, we can use one of the given points, let's say (2, -1, 3), and the normal vector (12, -12, -9) to write the equation of the plane in the point-normal form:
12(x - 2) - 12(y - (-1)) - 9(z - 3) = 0
Simplifying further:
12x - 24 - 12y + 12 - 9z + 27 = 0
12x - 12y - 9z - 9 = 0
4x - 4y - 3z - 3 = 0
Thus, the equation of the plane passing through the points (2, -1, 3), (5, 4, 6), and (-3, -3, -3) is 4x - 4y - 3z - 3 = 0.
This equation represents all the points (x, y, z) that lie on the plane. By substituting any point into the equation, we can determine if it lies on the plane or not. The coefficients of x, y, and z in the equation (4, -4, and -3) represent the direction of the normal vector of the plane, indicating the orientation of the plane in three-dimensional space.
Learn more about equation of the plane here
https://brainly.com/question/30655803
#SPJ11
please help me find m<1 before 11:59 PM!

Answers
Answer:
129 degrees
Step-by-step explanation:
add the interior angles: 62 + 67 = 129
subtract your answer from 180 to get the exterior angle of the interior angle that is opposite to the given angles
67+62
Answer
129

the producer of a certain bottling equipment claims that the variance of all its filled bottles is 0.027 or less. a sample of 30 bottles showed a standard deviation of 0.2. calculate the p-value of the test to four decimal places.
Answers
The p-value of the test of the producer of certain bottling equipment claims that the variance of all its filled bottles is 0.027 or less. a sample of 30 bottles showed a standard deviation of 0.2. is between 0.025 and 0.05.
What does the p-value tell you?The likelihood that the null hypothesis is correct is expressed by the p-value. The likelihood that the alternative hypothesis is correct is (1 - p-value). A little p-value indicates that the findings are repeatable. A big effect or a significant theoretical, clinical, or practical significance is indicated by a low p-value.
How is the p-value calculated?The sample data, test type, and sampling distribution of the test statistic under the null hypothesis are used to determine the p-value (lower-tailed test, upper-tailed test, or two-sided test). The formula for calculating the p-value for a lower-tailed test is: p-value = P(TS ts | H 0 is true) = cdf (ts)
The p-value of the test of the producer of certain bottling equipment claims that the variance of all its filled bottles is 0.027 or less. a sample of 30 bottles showed a standard deviation of 0.2. is between 0.025 and 0.05.
to learn more about p-value click the following link:-
https://brainly.com/question/24756209
#SPJ4
help pls pls help pls

Answers
Answer:
Step-by-step explanation:
See attachment

a container holds 18 identical boxes. determine how many containers can be filled completely by 300 similar boxes
Answers
Answer:
16
Step-by-step explanation:
300/18 is 16.6 but then the box isn't completely full so round down to get 16.
Answer:
\(\frac{50}{3}\)
Decimal Form: 16.666...
Mixed Number: \(16\frac{2}{3}\)
Step-by-step explanation:
Rewrite it into a fraction
\(\frac{1}{18} =\frac{x}{300}\)
Find x
Step 1: Cross Multiply
18 ⋅ x = 18x
1 ⋅ 300 = 300
Step 2: Turn into a ratio
18x : 300
Step 3: Divide Both sides by 18
\(\frac{18x}{18} =\frac{300}{18}\)
Cancel the 18's in \(\frac{18x}{18}\) by themselves, that leaves us with x
\(x = \frac{300}{18}\)
Step 4: Simplify
\(x = \frac{50}{3}\)
Decimal Form: 16.666...
Mixed Number: \(16\frac{2}{3}\)
If f(x) + x^2[f(x)]^5 = 34 and f(1) = 2, find f '(1). F '(1) = Use implicit differentiation to find an equation of the tangent line to the curve at the given point. y sin 12x = x cos 2y, (pi/2, pi/4)
Answers
To find the derivative of f(x) at x = 1, we can use the formula for implicit differentiation:
d/dx[f(x) + x^2[f(x)]^5] = 0
Substituting the given values, we get:d/dx[f(1) + 1^2[f(1)]^5] = 0
d/dx[2 + 1[2]^5] = 0
Solving for the derivative, we get:d/dx[2 + 1[2]^5] = 0
d/dx[2 + 32] = 0
0 + 32 = 0
Therefore, the derivative of f(x) at x = 1 is 32.
To find the equation of the tangent line to the curve at the given point (pi/2, pi/4), we can use the formula for the slope of a tangent line:
m = f'(x) = d/dx[y sin 12x] / d/dx[x cos 2y]
Substituting the given values, we get:m = d/dx[pi/4 sin 12(pi/2)] / d/dx[pi/2 cos 2(pi/4)]
m = d/dx[pi/4 sin 6pi] / d/dx[pi/2 cos pi/2]
m = 0 / 0
Since the derivative of the numerator is 0 and the derivative of the denominator is 0, the slope of the tangent line is undefined. This means that the tangent line is vertical and parallel to the y-axis.
The equation of the tangent line at the given point is therefore of the form:
x = c
where c is the x-coordinate of the given point, which is pi/2. Therefore, the equation of the tangent line is:
x = pi/2
Note that this is just the equation of a vertical line with an x-intercept at pi/2.
Learn More about Implicit differentiation here:
https://brainly.com/question/17018960
#SPJ4
.
Steven borrows $60,000 for school. The interest rate is 6.5%. He wants to pay off the loan in 12 years. What would be the simple interest rate?
$4,680
$4,680,000
$44,000
$46,800
Answers
The simple interest rate is $46,800
What is simple interest?
Simple interest serves as the interest that is based on the principal amount of a loan or in some cases the deposit in a savings account.
interest rate = 6.5%= 6.5/100= 0.065
time = 12 years
principal = $60,000
Simple interest formular =(Principal x Interest Rate x Time)/100
Simple interest = (12* 0.065* 60000)/100
=$46,800
Therefore, simple interest rate is $46,800
Learn more about simple interest at:
https://brainly.com/question/20690803
#SPJ1
Suppose the mean income of firms in the industry for a year is 9090 million dollars with a standard deviation of 1515 million dollars. If incomes for the industry are distributed normally, what is the probability that a randomly selected firm will earn less than 103103 million dollars
Answers
It is highly unlikely that a firm in this industry will earn less than 103 million dollars.
z = (x - μ) / σ
z = (103 - 9090) / 1515 = -5.38
The probability of a firm earning less than -5.38 standard deviations from the mean is very low, approximately 0.00000003. This means that the probability of a randomly selected firm earning less than 103 million dollars is extremely low, less than 0.00000003 or 0.000003%.
Probability is a mathematical concept that measures the likelihood of an event occurring. It is a way to quantify uncertainty and express it as a numerical value between 0 and 1. A probability of 0 indicates that the event is impossible, while a probability of 1 indicates that the event is certain.
Probabilities can be calculated using various methods, including the classical, empirical, and subjective approaches. The classical approach is based on the assumption that all outcomes are equally likely, while the empirical approach is based on observed data. The subjective approach involves using personal beliefs and opinions to estimate the probability of an event.
To learn more about Probability visit here:
brainly.com/question/30034780
#SPJ4
do exponential functions have horizontal asymptotes?
Answers
9514 1404 393
Answer:
yes
Step-by-step explanation:
The parent function e^x has a horizontal asymptote at y=0.

A student claims that the sum of a rational number and an irrational number is always irrational. Is the claim correct? No. The claim is incorrect because 2 + √ 4 = 2 + 2 = 4 , and 4 is a rational number. No. The claim is incorrect because 2 plus square root of 4 is equal to 2 plus 2 is equal to 4, and 4 is a rational number. No. The claim is incorrect because 2 + 1 √ 4 = 2 + 1 2 = 5 2 , and 5 2 is a rational number. No. The claim is incorrect because 2 plus the fraction with numerator 1 and denominator square root of 4 is equal to 2 plus 1 half is equal to 5 halves, and 5 halves is a rational number. Yes. The claim is correct because 3 π + 4 π = 7 π , and 7 π is an irrational number. Yes. The claim is correct because 3 pi plus 4 pi is equal to 7 pi, and 7 pi is an irrational number. Yes. The claim is correct because √ 16 + π = 4 + π , and 4 + π is an irrational number. Yes. The claim is correct because square root of 16 plus pi is equal to 4 plus pi, and 4 plus pi is an irrational number.
Answers
The correct option regarding whether the sum of a rational number and an irrational number is always irrational is given by:
Yes. The claim is correct because √ 16 + π = 4 + π , and 4 + π is an irrational number.
What are rational and irrational numbers?Rational numbers are numbers that can be represented by fractions, such as terminating decimals.Irrational numbers are numbers that cannot be represented by fractions, such as non-terminating decimals and non-exact roots.
The sum of a terminating decimal with a non-terminating decimal always results in a non terminating decimal, that is, the sum of a rational number with an irrational number is always irrational, and the correct option is given by:
Yes. The claim is correct because √ 16 + π = 4 + π , and 4 + π is an irrational number.
More can be learned about rational and irrational numbers at brainly.com/question/17232771
#SPJ1
If John has 10 apples and he associate Lily stole 1. How many oranges does he have?
Answers
Answer: it is 9 because 10 - 1 = 9
Step-by-step explanation:
Answer:
Answer 9 because 10-1=9
Step-by-step explanation:
If you have 10 apples and if I stole one from you then it will 9.
What is the probability that the test will fail to decide
is true when in reality =72. 5?
Answers
Determined by various factors such as sample size, statistical significance, and the chosen level of confidence. the probability that the test will fail to decide that the true value is 72.5 when it is indeed 72.5.
In order to calculate the probability of a Type II error, one would need to know the specific details of the test being used, such as the sample size, the statistical power of the test, and the chosen level of significance.
In general, the probability of a Type II error increases as the sample size decreases and the level of significance decreases. This means that if the test being used is not sufficiently powered or if the level of confidence is too low, there is a higher probability of failing to detect a true effect.
If the test is not able to accurately determine if the statement is true or not when the actual value is 72.5, then there is a possibility that a Type II error has occurred. The probability of this error depends on the specific details of the test being used and cannot be determined without further information.
The probability of a test failing to decide a certain hypothesis is true, when it is actually true, can be determined using the concept of Type II error or false negative rate. In statistical hypothesis testing, Type II error (β) refers to the probability of failing to reject a false null hypothesis. These factors influence the power of the test, which is the probability of correctly rejecting the null hypothesis when it is false. The power of the test (1 - β) is complementary to the probability of making a Type II error.
In this case, the null hypothesis (H0) could be that the value is not equal to 72.5,
while the alternative hypothesis (H1) states that the value is equal to 72.5.
The probability you are looking for is the Type II error rate when the true value is 72.5.
Learn more about sample size here:
https://brainly.com/question/31734526
#SPJ11
What is the contrapositive of the following statement
If two triangles are congruent, then their corresponding angles are congruent
Answers
Answer:/Step-by-step explanation:
If a triangle is not equiangular, then it does not have three congruent angles. If two triangles are congruent, then their corresponding angles are congruent. If the corresponding angles of two triangles are congruent, then the triangles are congruent.
what is the slope of the line that passes through the points (6, -5) and (6, -4)?
Answers
Answer (y2 -y1) / (x2 - x1)
hope this helps
Answer:
(y2 -y1) / (x2 - x1)
Step-by-step explanation:
Use that formula. The answer should be -3/0 which doesn't make sense. Are you sure you have your x values correct? Since in that case, it would be a straight line and the equation for that would be x = 6 since it is a straight line up with no y-intercept.
the issues surrounding the levels and structure of executive compensation have gained added prominence in the wake of the financial crisis that erupted in the fall of 2008. based on the 2006 compensation data obtained from the securities and exchange commission (sec) website, it was determined that the mean and the standard deviation of compensation for the 524 highest paid ceos in publicly traded u.s. companies are $10.82 million and $10.25 million, respectively. an analyst randomly chooses 46 ceo compensations from 2006 for analysis. true or false: the sampling distribution of the sample mean is approximately normally distributed.
Answers
The central limit theorem tells us that the distribution of the sample mean will be approximately normal if the sample size is sufficiently large. This information can be used to calculate the standard error and construct confidence intervals.
The sampling distribution of the sample mean is approximately normally distributed.
This statement is true. When the sample size is large\((n ≥ 30),\) the sampling distribution of the sample mean is approximately normally distributed. The sample mean is the mean of the sample's measurements, while the sampling distribution of the sample mean is the distribution of all possible sample means with a particular sample size.The central limit theorem guarantees that the sampling distribution of the sample mean is approximately normal if the sample size is large enough. This is due to the fact that the distribution of the population is not necessary. This theorem allows us to use the normal distribution in inferential statistics, making it an important theorem in statistics. When the sample size is less than 30, it is appropriate to use the t-distribution instead of the normal distribution because the t-distribution takes into account the extra uncertainty generated by the smaller sample size.The sampling distribution is critical to statistical inference because it helps us estimate population parameters by making inferences based on sample statistics. For instance, suppose we want to know the mean salary of all the employees in a firm. We could take a random sample of employees and calculate their average salary.
for such more questions on central limit theorem
https://brainly.com/question/13652429
#SPJ11
Finding the volume. help lol!!

Answers
Hope this helps and good luckkkkk :)
Answer:
5128 2/3 m³
Step-by-step explanation:
Cone Volume Formula: πr²h/3
3.14(14²) * 25/3
3.14(196) * 25/3
615.44 * 25/3
15386/25 * 25/3
GCD = 75
46158/75 * 625/75
46158/3 * 25/75
15386/3 * 25/25
15386/3
5128 2/3 m³ is the volume.
Find the measure of angle A. 7x-2
80°
9x+6

Answers
Round 36.268 to the nearest whole number.
Answers
The answer after rounding is 36
the sum of 12 terms of an arithmetic series is 186 and the 20th term is 83. find the sum of 40 terms of the series.
Answers
The Sum of 40 terms of the Arithmetic Sequence is 3,420..
Arithmetic Series is defined as a sum of the terms of arithmetic progression or sequence.
An Arithmetic progression is a sequence of terms in which the difference between two consecutive terms is a constant number.
We have following information about series
sum of 12 terms of an arithmetic series (S₁₂) = 186
the 20th term of arithmetic sequence = 83
i.e., a₂₀ = 83
As we know that nth term of arithmetic progression is aₙ= a + (n-1)d
where , a---> first term of sequence
n ----> nth term
d -----> constant difference between two consecutive terms
put n= 20 in above formula we get,
83 = a + (20-1 )d = a+ 19d ----(1)
Now , Using the sum of n arithmetic terms formula, Sₙ = n/2 ( 2a + (n-1)d)
so, for n = 12
186 = 12/2 ( 2a + 11d ) => 2a + 11d = 31 ---(2)
Solving equations (1) and (2) we get,
27d = 135 => d = 5
putting the value of d in equation (1)
83 = a + 19×5 => a = 83 - 95 = -12
thus sequence is like as -12, -7 , -2 , ------
Sum of first 40 terms of arithmetic sequence (S₄₀) = 40/2 ( 2× (-12) + 39d ) = 20 ( -24 + 39×5)
= 20( 171) = 3,420
So, required result is 3,420..
To learn more about Arithmetic Sequence, refer:
https://brainly.com/question/10694174
#SPJ4
Solve the inequality x + 2 > 6.
Answers
Answer:
x > 4
Step-by-step explanation:
x + 2 > 6
-2 -2
x > 4
If A ⊂ X then the boundary Bd(A) is defined by the expressionBd(A) = A ∩ X − Aa) show that inf(A) and Bd(B) are disjoint and their union is the closure of A.b) show that Bd(A) is empty if and only if A is both open and closed
Answers
a) To show that inf(A) and Bd(A) are disjoint and their union is the closure of A, we need to prove two things:
1. inf(A) and Bd(A) are disjoint: Suppose there exists an element x that belongs to both inf(A) and Bd(A). Then, x belongs to A and its closure, Abar, and it also belongs to the boundary of A, Bd(A). This means that x is a limit point of both A and its complement, X-A, which implies that x belongs to the closure of both A and X-A. But since A is a subset of X, we have X-A ⊆ X-A ∪ A = X, and therefore x belongs to the closure of X, which is X itself. This contradicts the assumption that x belongs to A, which is a proper subset of X. Hence, inf(A) and Bd(A) are disjoint.
2. The union of inf(A) and Bd(A) is the closure of A: Let x be a limit point of A. Then, by definition, every open set U containing x must intersect A in a non-empty set. Now, consider two cases:
- If x is not a boundary point of A, then there exists an open set U such that U ∩ A is either empty or equal to A itself. Since x is a limit point of A, we know that U must intersect A in a non-empty set, and hence U ∩ A ≠ ∅. Therefore, U ∩ A = A, which implies that x ∈ A and hence x ∈ inf(A).
- If x is a boundary point of A, then every open set U containing x must intersect both A and X-A in non-empty sets. Hence, U ∩ A ≠ ∅ and U ∩ X-A ≠ ∅. This means that x belongs to both Abar and (X-A)bar, the closures of A and X-A respectively. Therefore, x belongs to the boundary of A, Bd(A).
Since every limit point of A belongs to either inf(A) or Bd(A), we have inf(A) ∪ Bd(A) = Abar, the closure of A.
b) Now, we will show that Bd(A) is empty if and only if A is both open and closed.
First, suppose that Bd(A) is empty. This means that every point in A is an interior point or an exterior point of A, but not a boundary point. Since every point in A is either an interior or exterior point, we can conclude that A is both open and closed.
Conversely, suppose that A is both open and closed. Then, by definition, every boundary point of A must be a limit point of both A and its complement, X-A. But since A is closed, its complement, X-A, is open. Therefore, if a point x is a limit point of X-A, then there exists an open set U containing x that is entirely contained in X-A. This implies that U ∩ A = ∅, and hence x cannot be a boundary point of A. Therefore, Bd(A) must be empty.
To know more about sets refer here
https://brainly.com/question/13572279
SPJ11
Consider the following statements: If it snows, I am cold. If it rains, I am wet. If I am wet and it is windy, I am cold. (a) Choose names for each atomic proposition in the text above and write down its intended interpretation. (b) Translate each statement in the text above to a proposition. (c) Find a truth assignment that satisfies all of the sentences above plus the statement "I am cold." (That is, all of the sentences are true in that truth assignment.) (d) Find a truth assignment that satisfies all of the sentences above plus the statement "I am not cold." (e) Treating the propositions from (b) as axioms, prove the proposition corresponding to "If I am not cold and it is windy, then it is not raining."
Answers
(a) Let's assign names to each atomic proposition:
1. P: It snows. 2. Q: I am cold. 3. R: It rains. 4. S: I am wet. 5. W: It is windy.
(b) Translating each statement: 1. If P, then Q. 2. If R, then S. 3. If S and W, then Q. (c) Truth assignment satisfying all sentences + "I am cold": Let's assume the following truth values: P: TrueQ: TrueR: TrueS: True W: True
With this assignment, all the given sentences are true:
1. If it snows (True), I am cold (True) - True.
2. If it rains (True), I am wet (True) - True.
3. If I am wet (True) and it is windy (True), I am cold (True) - True.
"I am cold" - True.
(d) Truth assignment satisfying all sentences + "I am not cold":
Let's assume the following truth values:
P: True
Q: False
R: True
S: True
W: True
With this assignment, all the given sentences are true:
1. If it snows (True), I am cold (False) - True.
2. If it rains (True), I am wet (True) - True.
3. If I am wet (True) and it is windy (True), I am cold (False) - True.
"I am not cold" - True.
(e) Proof of the proposition: "If I am not cold and it is windy, then it is not raining":
To prove this proposition using the given axioms, we assume the following:
1. A: I am not cold.
2. W: It is windy.
We need to show that ¬R holds, i.e., it is not raining.
Using the given axioms, we can derive the proof as follows:
1. A → S (From axiom "If R, then S" by contrapositive)
2. S ∧ W → Q (From axiom "If S and W, then Q")
3. A → Q (Transitivity of implication from 1 and 2)
4. A → (Q ∧ ¬Q) (Combining A with its negation)
5. A → ¬Q (From 4 by contradiction)
6. (A ∧ W) → ¬R (From axiom "If S and W, then Q" by contrapositive)
Thus, using the given axioms, we have proved the proposition "If I am not cold and it is windy, then it is not raining" as (A ∧ W) → ¬R.
Learn more about atomic proposition here: brainly.com/question/30479730
#SPJ11
answer it this is for high school student

Answers
\( \sf \: 1. \bigg[ \frac{4 + ( - 5)}{ - 2 - 3} \bigg]\bigg[ \frac{14 + ( - 21)}{ 2 - 8} \bigg] \\ \)
\( \sf \longrightarrow \: \bigg[ \frac{4 + ( - 5)}{ - 2 - 3} \bigg]\bigg[ \frac{14 + ( - 21)}{ 2 - 8} \bigg] \\ \)
\( \sf \longrightarrow \: \bigg[ \frac{4 - 5}{ - 2 - 3} \bigg]\bigg[ \frac{14 - 21}{ 2 - 8} \bigg] \\ \)
\( \sf \longrightarrow \: \bigg[ \frac{ - 1}{ - 5} \bigg]\bigg[ \frac{ - 7}{ - 6} \bigg] \\ \)
\( \sf \longrightarrow \: \frac{1}{ 5} \times \frac{ 7}{ 6} \\ \)
\( \sf \longrightarrow \: \frac{7}{30} \\ \)
C) 7/30 ✅
________________________________
\( \sf \: 2. \bigg[ \frac{7+ ( - 6)}{ - 4 - 9} \bigg]\bigg[ \frac{20 + ( - 45)}{ 8 - 2} \bigg] \\ \)
\( \sf \longrightarrow\bigg[ \frac{7 + ( - 6)}{ - 4 - 9} \bigg]\bigg[ \frac{20 + ( - 45)}{ 8 - 2} \bigg] \\ \)
\( \sf \longrightarrow\bigg[ \frac{7 - 6}{ - 4 - 9} \bigg]\bigg[ \frac{20 - 45}{ 8 - 2} \bigg] \\ \)
\( \sf \longrightarrow\bigg[ \frac{1}{ - 4 - 9} \bigg]\bigg[ \frac{ - 25}{ 8 - 2} \bigg] \\ \)
\( \sf \longrightarrow\bigg[ \frac{1}{ - 13} \bigg]\bigg[ \frac{ -25}{ 6} \bigg] \\ \)
\( \sf \longrightarrow \: \frac{ - 25}{ - 78} \\ \)
\( \sf \longrightarrow \: \frac{ 25}{ 78} \\ \)
A] 25 / 78 ✅
________________________________
\( \sf \: 3. \bigg[ \frac{4+ ( - 5)}{ - 2 - 4} \bigg]\bigg[ \frac{18 + ( - 36)}{ 7 - 3} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{4+ ( - 5)}{ - 2 - 4} \bigg]\bigg[ \frac{18 + ( - 36)}{ 7 - 3} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{4 - 5}{ - 2 - 4} \bigg]\bigg[ \frac{18 - 36}{ 7 - 3} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{-1}{ - 6} \bigg]\bigg[ \frac{18 - 36}{ 7 - 3} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{-1}{ - 6} \bigg]\bigg[ \frac{-18}{ 4} \bigg] \\ \)
\( \sf \longrightarrow \frac{18}{ - 24} \\ \)
\( \sf \longrightarrow -\frac{6}{ 8} \\ \)
\( \sf \longrightarrow -\frac{3}{ 4} \\ \)
C] -3/4 ✅
________________________________
\( \sf \: 4. \bigg[ \frac{7+ ( - 3)}{ - 6 - 2} \bigg]\bigg[ \frac{18 + ( - 6)}{ 6- 7} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{7+ ( - 3)}{ - 6 - 2} \bigg]\bigg[ \frac{18 + ( - 6)}{ 6- 7} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{7- 3}{ - 6 - 2} \bigg]\bigg[ \frac{18 - 6}{ 6- 7} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{4}{ - 6 - 2} \bigg]\bigg[ \frac{12}{ 6- 7} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{4}{ - 8} \bigg]\bigg[ \frac{12}{ -1} \bigg] \\ \)
\( \sf \longrightarrow \frac{48}{ 8} \\ \)
\( \sf \longrightarrow \frac{6}{ 1} \\ \)
\( \sf \longrightarrow 6 \\ \)
D] 6 ✅
________________________________
\( \sf \: 5. \bigg[ \frac{8+ ( - 2)}{ - 5- 6} \bigg]\bigg[ \frac{40 + ( - 48)}{ 9 - 8} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{8+ ( - 2)}{ - 5- 6} \bigg]\bigg[ \frac{40 + ( - 48)}{ 9 - 8} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{8 - 2}{ - 5- 6} \bigg]\bigg[ \frac{40 - 48}{ 9 - 8} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{6}{ - 5- 6} \bigg]\bigg[ \frac{-8}{ 9 - 8} \bigg] \\ \)
\( \sf \longrightarrow \bigg[ \frac{6}{ - 11} \bigg]\bigg[ \frac{-8}{ 1} \bigg] \\ \)
\( \sf \longrightarrow \frac{-48}{ - 11} \\ \)
\( \sf \longrightarrow \frac{48}{ 11} \\ \)
B] 48/11 ✅
________________________________
Will a large-sample confidence interval be valid if the population from which the sample is taken is not normally distributed? explain
Answers
A normal distribution is a type of continuous probability distribution for a real-valued random variable in statistics.
Yes, the large-sample confidence interval will be valid.
What is meant by normal distribution?A normal distribution is a type of continuous probability distribution for a real-valued random variable in statistics.
The normal distribution, also known as the Gaussian distribution, is a symmetric probability distribution about the mean, indicating that data near the mean occur more frequently than data far from the mean.
The confidence interval will be valid regardless of the shape of the population distribution as long as the sample is large enough to satisfy the central limit theorem.
What does a large sample confidence interval for a population mean?A sample is considered large when n ≥ 30.
By 'valid', it means that the confidence interval procedure has a 95% chance of producing an interval that contains the population parameter.
To learn more about normal distribution, refer to:
brainly.com/question/23418254
#SPJ4
Solve y3 = −125.
please please help
Answers
Answer:
pretty sure it's -5
Step-by-step explanation:
the cubed root if 125 is 5 so you just make it negative
Answer:
y = 5
Step-by-step explanation:
Let's solve your equation step-by-step.
\( y{}^{3}=125\)
Step 1: Take cube root.
\( \sf \: y= {(125)} ^ {( \frac{1}{3} )}\)
y=5