3+5+7+.....+103 determine the general term
Answers
Answer:
\(a_{n}\) = 2n + 1
Step-by-step explanation:
there is a common difference in the first 3 terms, that is
5 - 3 = 7 - 5 = 2
this indicates the sequence could be arithmetic with nth term
\(a_{n}\) = a₁ + d(n - 1)
where a₁ is the first term and d the common difference
here a₁ = 3 and d = 2 , then the general term is
\(a_{n}\) = 3 + 2(n - 1) = 3 + 2n - 2 = 2n + 1
Related Questions
(5x+30)=7x ??
Can anyone help me
Answers
Answer:
the answer is x=15.....

Answer:
Step-by-step explanation:
(5x+30)=7x Subtract 7x from both sides. 5x+30−7x=0 Combine 5x and −7x to get −2x. −2x+30=0 Subtract 30 from both sides. Anything subtracted from zero gives its negation. −2x=−30 Divide both sides by −2. x= −2 −30 Divide −30 by −2 to get 15. answer should be x=15
Which of the following are solutions to the quadratic equation below?
Check all that apply.
x²+7x-8=0
A. -1
B. 2
C. -4
D. -8
E. 1

Answers
Therefore, the solutions to the quadratic equation x² + 7x - 8 = 0 are -8 and 1. The answers are D and E.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It typically consists of variables, constants, and mathematical operations. Equations can be solved by manipulating the expressions to find the value of the variables that satisfy the equation. Equations can be used to model real-world situations, and they are an important tool in many fields, including mathematics, physics, engineering, and economics.
Here,
To check which values are solutions to the quadratic equation, we can substitute each value into the equation and see if it equals zero.
Substituting -1 into the equation:
(-1)² + 7(-1) - 8 = 1 - 7 - 8 = -14, which is not equal to zero.
Substituting 2 into the equation:
2² + 7(2) - 8 = 4 + 14 - 8 = 10, which is not equal to zero.
Substituting -4 into the equation:
(-4)² + 7(-4) - 8 = 16 - 28 - 8 = -20, which is not equal to zero.
Substituting -8 into the equation:
(-8)² + 7(-8) - 8 = 64 - 56 - 8 = 0, which is equal to zero. Therefore, -8 is a solution to the equation.
Substituting 1 into the equation:
1² + 7(1) - 8 = 1 + 7 - 8 = 0, which is equal to zero. Therefore, 1 is a solution to the equation.
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
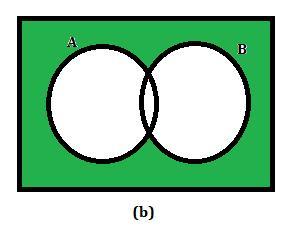
Let A, B, and C be events relative to the sample space S. Using Venndiagrams, shade the areas representing events:
a.) (A∩B)′
b.) (A∪B)′
c.) (A∩C)∪B
Answers
If A, B and C be events relative to the sample space S, then the Venn diagram of the representing event has been plotted
Let A, B and C be events relative to the sample space S.
The sample space is the set of all possible outcomes of the experiment.
The Venn diagram is the pictorial representation of the sample space of the experiment by using the circles and the overlapping of the circles.
Here we have to plot the each representing events using the Venn diagram representation
Part a
The event is (A ∩ B)'
Plot the Venn diagram
Part b
The event is (A ∪ B)'
Plot Venn diagram
Part c
The event is (A ∩ C) ∪ B
Plot the Venn diagram
Therefore, the Venn diagram of the each event has been plotted
Learn more about Venn diagram here
brainly.com/question/29301560
#SPJ4


Find the slope from this table
X Y
2 4
3 7
4 10
Answers
Answer:The relationship isn’t constant
Step-by-step explanation:
In a 30-60-90 triangle the long leg is half the hypotenuse.
never
always
sometimes
Answers
Answer:
Never
Step-by-step explanation:
In a 30-60-90 triangles:
The length of a hypotenuse side is twice the length of the shorter leg
The length of the Longer side is \(\sqrt{3}\) times the shorter leg.
The 1st, 2nd and 3rd terms of a geometric progression are the 1st, 9th and 21st terms of an arithmetic progression respectively. Given that the 1st term of both progressions is 8 and the common ratio of the geometric progression, r not equation of 1 .Find .
a.The value of r
b.the 4th term of each progression
Answers
a. The value of r = 3, -1/2.
b. The 4th term of each progression;
for r = 3; AP = 14, GP = 216.for r = -1/2; AP = 7/2, GP = 1/2.What is defined by AP and GP?An Arithmetic Progression (AP) is a collection of terms with the same differences between them. In a Geometric Progression (GP), each successive term is created by multiplying the common ratio by previously acted.As, per the given question;
Let the first three terms of GP be a, ar, and ar².
The 1st, 2nd and 3rd terms of a GP equals 1st, 9th and 21st terms of an AP respectively.
First term are equal; a = a2nd term GP = 9th term of AP; ar = a + 8d. 3rd term GP = 21st term of AP; ar² = a + 20d.where, 'r' is the common ratio in GP and 'd' is the common difference in AP.
Part 1: Multiply equation 1 by 5 and 2 by 2 and subtract 1 from 2.
2ar² - 5ar - 3a = 0
Put a = 8 and solving.
16r² - 40r - 24 = 0.
Factorising the above equation;
(r - 3)(2r + 1) = 0
Thus, r = 3 and r = -1/2
Part 2:
Case 1: For r = 3; a =8;
ar = a + 8d
d = 2.
Thus, 4th term = a + 3d
= 8 + 3×2
4th term = 14.
For GP;
4th term = ar³
= 8(3)³
4th term = 216.
Case 2: For r = -1/2; a =8;
ar = a + 8d
d = -3/2
Thus, 4th term = a + 3d
= 8 + 3×(-3/2)
4th term = 7/2
For GP;
4th term = ar³
= 8(-1/2)³
4th term = -1.
Therefore, the values for the r and 4th term is estimated.
To know more about geometric progression, here
https://brainly.com/question/25461416
#SPJ9
Which of the values listed is a prime number?
A. 10
B. 15
C. 27
D. 29
Answers
Answer:
D. 29
Step-by-step explanation:
A. 10 = 2 × 5 not prime
B. 15 = 3 × 5 not prime
C. 27 = 3³ not prime
D. 29 = 1 × 29 prime
Answer:
29
Step-by-step explanation:
A prime number is a number that can't be divided by any number other than itself or 1.
10
1*10
2*5
5*2
10*1
NOT A PRIME NUMBER
15
1*15
3*5
5*3
15*1
NOT A PRIME NUMBER
27
1*27
3*9
9*3
27*1
NOT A PRIME NUMBER
29
1*29
29*1
PRIME NUMBER
FILL IN THE BLANK
If an equation has one solution.. It means.. Only ______ Number will make this equation true. Can you think of an equation that would make this equation true?
Answers
Answer:
One
....................
Answer:
1
Step-by-step explanation:
Because if you plug in any other number than that 1 number (the solution) it will make the equation false. So, there will only be 1 number that can make the equation true.
The volume of this rectangular prism is 160 cubic yards. What is the surface area?
10 yd
surface area =
Submit
0
4 yd
square yards
4
Answers
Answer: The surface area of the rectangular prism is approximately 4 square yards.
Step-by-step explanation: Given that the volume of the rectangular prism is 160 cubic yards, we can find the dimensions of the prism using the formula:
V = lwh
where V is the volume, l is the length, w is the width, and h is the height.
So, we have:
160 = lwh
Now, we need to find two other measurements in order to calculate the surface area of the rectangular prism. However, we do not have enough information to find all three dimensions. Therefore, we will assume one dimension and find the other two.
Let's assume that the height of the rectangular prism is 10 yards. Then, we can rearrange the formula for the volume to solve for the product of the length and width:
lw = V/h = 160/10 = 16
Now, we have two equations:
lw = 16
wh = 160/10 = 16
Solving for w in the first equation, we get:
w = 16/l
Substituting this expression for w in the second equation, we get:
l(16/l)h = 16
Simplifying, we get:
h = 1
Therefore, the dimensions of the rectangular prism are:
length = l
width = 16/l
height = 10
Now, we can calculate the surface area of the rectangular prism using the formula:
SA = 2lw + 2lh + 2wh
Substituting the values we found, we get:
SA = 2(l(16/l)) + 2(l(10)) + 2((16/l)(10))
SA = 32/l + 20l + 160/l
To find the minimum value of this expression, we can take its derivative with respect to l and set it equal to zero:
dSA/dl = -32/l^2 + 20 + (-160/l^2)
0 = -32/l^2 + 20 - 160/l^2
52/l^2 = 20
l^2 = 52/20
l ≈ 1.44
Substituting this value of l back into the expression for SA, we get:
SA ≈ 4 square yards
Therefore, the surface area of the rectangular prism is approximately 4 square yards.
1. [1/4 Points] DETAILS PREVIOUS ANSWERS For each absolute value inequality, write an equivalent compound inequality. (a) (x +31 < 1 is equivalent to ____ < x+3< ______
b) |x-6|≥ 2 is equivalent to x-6≤ ______
or x-6≥
Answers
The inequalities are :
x + 31 < 1 ⇒ x < - 30 ⇒ x + 3 < -27
|x - 6| ≥ 2 ⇒x- 6 ≥ 2 and 6 - x ≤ 2
What are inequalities ?An inequality is a relation that compares two numbers or other mathematical expressions in an unequal way. The most frequent application is to size-compare two integers on a number line.
The occurrence of an unfair and/or uneven distribution of opportunities and resources among the people that make up a society is referred to as inequality. To different individuals and in various settings, the word "inequality" may indicate different things.
Inequality is a connection between two expressions or values that is not equal to each other. Therefore, inequality emerges from a lack of balance.
The inequalities are :
x + 31 < 1 ⇒ x < - 30 ⇒ x + 3 < -27
|x - 6| ≥ 2 ⇒x- 6 ≥ 2 and 6 - x ≤ 2
To learn more about Inequality refer to :
https://brainly.com/question/13589585
#SPJ1
Solve −x−6≥−5 or −2x−5>4 and write the solution in interval notation. Note: Use improper fractions, if necessary.
Answers
Answer:
(-∞, -1]
Step-by-step explanation:
−x−6≥−5
-x≥1
x≤-1
−2x−5>4
-2x>9
x<-9/2
So x < -9/2 V x ≤ -1
Answer:
(−∞,∞)
Step-by-step explanation:
5x - 4 ≤ - 3
5x ≤ 1
x ≤ \(\frac{1}{5}\)
4x + 6 > 0
4x > - 6
x > - \(\frac{3}{2}\)
a, b, and c.1-1+7x+6yab-с —Submit Answer
Answers
The general formula for the polynomial function is
\(ax+by+c\)Following this formula, you have to identify a, b and c in the given polynomial
\(-1+7x+\frac{1}{6}y\)c is the term of the function that is not related to any variable, i.e. the number that is alone, so c = -1
a is the number that is related to the variable x, in the expression that value is a = -7
b is the number that is related to the variable y, in the expression that value is b = 1/6
if a teenager receives 4 tokens for finishing first place in an arcade game, which table correctly represents the realtionship between the number of tokens the teenager receives and the number of first place finishes the teenager completes?

Answers
Answer:
The first chart.
Step-by-step explanation:
The first table. The chart gives a ratio of 1:4, which is the same as the amount the teenager made.
Plzzzzzzz help right answer gets brainly

Answers
Answer:
C:"As time dragged on, she sang to pass the hours."
Step-by-step explanation:
Help it’s math work

Answers
Answer:
The First question's answer is AngleW = 77 degrees
The Second question's answe is x = 2
Step-by-step explanation:
First Question:
AngleW = 7x
AngleY = 6x + 11
Since Opposite Angles in a parallelogram are equal,
AngleW = AngleY
or
7x = 6x + 11
7x - 6x = 11
x = 11
Now that we know the value of x, we can find the value of angleW
AngleW = 7x
AngleW = 7(11)
Angle W = 77
Second Question:
LN = 20
UN = 5x
Since LN and KM are diagonals of the parallelogram, they bisect each other at point of contact, so, UN = 1/2LN
or
5x=1/2 × 20
5x = 10
x = 2
Write in word form 10x10
Answers
Answer:
ten times time
Step-by-step explanation:
ten time ten or ten multiple by ten
give brainliest please I need it to level up
Answer:
Ten times Ten or ten over ten
PLEASE ANSWER UNDER 5 MIN!!!! ily!!!!
what is the period of the sinusoidal function? enter your answer in the box.

Answers
Answer:
Step-by-step explanation:
10
Ws
pleas help i in exanm

Answers
6 * 3/8
Is the same as
6/1 * 3/8
Do you know how to multiply fractions
Position vs Time m The starting position of this object is The object is traveling at a velocity of m/s 15 12 Position (m) 0 1 2. 3 4. 5 Time (s)
Answers
Velocity = distance/ time
Starting position of object is 3 meters
Object is travelling at a velocity of (15-3)/(4-0) =
(15-3)/(4-0)= 12/4= 3 meters/second
How could Marc mathematically try to prove that he hit the ball near the top of the tower?While on the golf course last weekend Marc hit into the rough, landing the ball behind a tall tree. To get out of the scenario, his best option was to hit the ball high enough so it goes over the tree and hopefully comes down in the fairway for his next shot. So with a mighty swing, he hit the ball into the air and was surprised to see it hit near the top of a 300 foot tall tower that he had not noticed. The formula for this shot is h(x) = -16xsquared + 120x , where h is the height of the ball and x is the number of seconds the ball is in the air. How could Marc mathematically try to prove that he hit the ball near the top of the tower?While on the golf course last weekend Marc hit into the rough, landing the ball behind a tall tree. To get out of the scenario, his best option was to hit the ball high enough so it goes over the tree and hopefully comes down in the fairway for his next shot. So with a mighty swing, he hit the ball into the air and was surprised to see it hit near the top of a 300 foot tall tower that he had not noticed. The formula for this shot is h(x) = -16xsquared + 120x , where h is the height of the ball and x is the number of seconds the ball is in the air. How could Marc mathematically try to prove that he hit the ball near the top of the tower?
Answers
Answer:
To mathematically prove that Marc hit the ball near the top of the tower, he could use the equation h(x) = -16x^2 + 120x, where h is the height of the ball and x is the number of seconds the ball is in the air.
First, Marc would need to determine the maximum height the ball reached during its flight. This can be found by using the vertex formula, which is x = -b/2a. In this case, a = -16 and b = 120, so x = -120/(2*-16) = 3.75 seconds.
Next, Marc can substitute this value back into the original equation to find the maximum height the ball reached. h(3.75) = -16(3.75)^2 + 120(3.75) = 135 feet.
Since the tower is 300 feet tall, Marc could conclude that if the ball hit near the top of the tower, it would have reached a height close to 300 feet. Since the ball reached a maximum height of 135 feet, it is unlikely that it hit the top of the tower.
However, this calculation assumes that the tower is directly in line with Marc's shot and that the ball did not have any horizontal movement. In reality, the tower could have been to the left or right of the shot, and the ball could have had some horizontal movement, which would affect its height at impact. Therefore, this calculation can only provide a rough estimate and cannot definitively prove whether or not the ball hit near the top of the tower.
Elena receives $95 per year in simple interest from three investments totaling $2100 . Part is invested at 3%, part at 4%, and part at 5%. There is $1000 more invested at 5% than at 4%. Find the amount invested at each rate.
The amount invested at 3% is $
the amount invested at 4% is $
and the amount invested at 5% is $
Answers
The amount invested at 3% is $400, the amount invested at 4% is $700, and the amount invested at 5% is $1000.
Let's assume the amount invested at 4% is x dollars.
According to the given information, the amount invested at 5% is $1000 more than the amount invested at 4%.
So, the amount invested at 5% is (x + $1000).
The total amount invested is the sum of the amounts invested at each rate, which is $2100.
Therefore, we can write the equation:
x + (x + $1000) + (amount invested at 3%) = $2100
Now, we can calculate the amount invested at 3%.
We subtract the sum of the amounts invested at 4% and 5% from the total investment:
(amount invested at 3%) = $2100 - (x + x + $1000) = $2100 - (2x + $1000)
Given that Elena receives $95 per year in simple interest from the investments, we can use the formula for simple interest:
Simple Interest = Principal × Interest Rate
The interest earned from the investment at 3% is (amount invested at 3%) × 0.03, the interest earned from the investment at 4% is (amount invested at 4%) × 0.04, and the interest earned from the investment at 5% is (amount invested at 5%) × 0.05.
According to the problem, the total interest earned is $95.
So we can write the equation:
(amount invested at 3%) × 0.03 + (amount invested at 4%) × 0.04 + (amount invested at 5%) × 0.05 = $95
Now we can substitute the expression for (amount invested at 3%) and solve for x.
Once we have the value of x, we can calculate the amounts invested at 3%, 4%, and 5% using the given information.
For similar question on amount invested.
https://brainly.com/question/2720767
#SPJ8
The cordinates of three of the verticies of paralellogram ABCD are A(1,0), B(2,3) and C(3,2). What are the cordinates of the 4th Vertex and the point of intersection of the diagonals
Answers
Answer:
1) x cordinate x= 2
2) y cordinate y = -1
b)the point of intercowegwjpoeg is (2,1)
Step-by-step explanation:
Answer:
U ଏହାକୁ ଡିକୋଡେଡ୍ କରିନାହିଁ ତୁମେ ଏତେ ଅଦ୍ଭୁତ ଏବଂ ମୂକ ଲୋଲୋଲ୍ |
Step-by-step explanation:
Ten upright dominos of increasing height are lined up to be knocked down. The dominos are numbered 0 to 9. The smallest domino, #0, is 3.00 inches tall and will be toppled by a person to start the chain reaction. Each subsequent domino is 15% taller than the one before. What is the height of domino #9?
Answers
Answer:
8.604 in.
Step-by-step explanation:
We can use the formula for compound interest to find the height of domino #9:
A = P(1 + r)^n
where A is the final amount, P is the initial amount, r is the growth rate, and n is the number of compounding periods. In this case, P is the height of domino #0, r is 15% or 0.15, and n is 9 (since we want to find the height of domino #9).
Substituting the given values:
A = 3.00 in * (1 + 0.15)^9
Simplifying:
A = 3.00 in * 2.86797199
A ≈ 8.604 in
Therefore, the height of domino #9 is approximately 8.604 inches.
Jennifer is a wedding planner. She set up six chairs at each table for the reception. If t represents the number of tables, which of the following expressions represents the total number of chairs that she set up?
A. 6 + t
B. t + 6
C. 6t
D. t - 6
Answers
Answer: C. 6t
Step-by-step explanation:
T is unknown, but because you are only asked for the equation to figure out the total, you simply multiply the 6 chairs per t, or table together, 6t
16 emails to 6 text messages- 10 emails to 4 text messages proportional or not
Answers
Given:
16 emails to 6 text messages- 10 emails to 4 text messages
To find:
Whether 16 emails to 6 text messages- 10 emails to 4 text messages proportional or not.
Solution:
Check the ratio of emails to text. If the ratios are equal then the relation is proportional.
16 emails to 6 text messages.
\(\dfrac{Emails}{Text}=\dfrac{16}{6}\)
\(\dfrac{Emails}{Text}=\dfrac{8}{3}\)
\(\dfrac{Emails}{Text}=8:3\)
10 emails to 4 text messages.
\(\dfrac{Emails}{Text}=\dfrac{10}{4}\)
\(\dfrac{Emails}{Text}=\dfrac{5}{2}\)
\(\dfrac{Emails}{Text}=5:2\)
Since \(\dfrac{8}{3}\neq \dfrac{5}{2}\) or \(8:3\neq 5:2\), therefore, it is not proportional.
you can continue to tranform 12=5x-3 into simpler form by adding 3 to both sides to get 15=5x when x =3 do youu get true statement
Answers
Answer:
yes
Step-by-step explanation:
12+3=5x-3+3
15=5x
15=5(3)
15=15
Suppose that a study of elementary school students reports that the mean age at which children begin reading is 5.9 years with a standard deviation of 0.9 years. Step 1 of 2 : If a sampling distribution is created using samples of the ages at which 69 children begin reading, what would be the mean of the sampling distribution of sample means
Answers
Answer:
5.9 years.
Step-by-step explanation:
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
In this question:
Mean of the population is \(\mu = 5.9\)
If a sampling distribution is created using samples of the ages at which 69 children begin reading, what would be the mean of the sampling distribution of sample means?
By the Central Limit Theorem, the same population mean, of 5.9 years.
What is the base (area) of this

Answers
Answer:
3cm + 3cm+ 14/3cm + 14/3cm = base
Step-by-step explanation:
^^
Good luck!
Here, it will be 3 x 14/3 which is equal to 14 cm.
Thanks.
-3y-5=10 Show your work please, thank you.
Answers
Answer:
-5
Step-by-step explanation:
-3y = 10 + 5
-3y = 15
y = - 5
Answer:
hi
Step-by-step explanation:
-3y-5=10
-3y=10+5
-3y=15
y=15/ -3
y= -5
hope it helps
have a nice day
A cyclist is riding a bicycle whose wheels have a diameter of 1.6 feet. Suppose the wheels turn at a rate of 280 revolutions per minute. (a) Find the angular speed of the wheels in radians per minute. (b) Find the speed of the cyclist in feet per minute.
Answers
Answer: a. 1759.52 radians/minutes
b. 1407.62 feet/minutes
Step-by-step explanation:
Diameter = 1.6 feet
Radius = Diameter/2= 1.6/2 = 0.8 feet
N = 280 revolution
a. Angular speed(w) = 2πN
= 2π × 280
= 560π
= 560 × 3.142
= 1759.52 radians/minutes
Speed of cyclist = wr
= 1759.52 × 0.8
= 1407.62 feet/minutes