36 inch board is to be cut into three pieces so that the second piece is three times as long as the first piece and the third piece is five times as long as the first piece if X represents the length of the first piece find the length of all three pieces
Answers
Answer: the first one would be four then that times 3 would be 12 which is 2 and then 4 times 5 is 20 which would be the third then you could add to check and you would get 36
Step-by-step explanation:
Hope this helped
if something's not clear, write a comment I'll help

Related Questions
7) What does a multiplier of \( 1.2 \) mean?
Answers
A multiplier of 1.2 means the value is multiplied or increased by a factor of 1.2.
A multiplier is a term used to represent a factor by which a value is multiplied or increased. It is a numeric value that indicates the extent of the increase or expansion of a given quantity. Multiplication by a multiplier results in scaling or changing the magnitude of the original value.
A multiplier of 1.2 indicates that a value will be increased by 20% or multiplied by a factor of 1.2. This means that when the multiplier is applied to the original value, the resulting value will be 1.2 times the original.
Read more about multipliers:
brainly.com/question/15883095
What's the answer for this?

Answers
Answer:
50
Step-by-step explanation:
if 50 degrees is the angle across from b, then 50 is b. 50 applies to b as well. whatever is across from it is the same thing. all of the angles should add up to 360 at an intersection.
20 points, I give out 20 points per question and I ask a lot of question

Answers
PLS HELP ME!!!! I WILL GIVE BRAINLIEST!!!!
How cold you find the combined area of all faces of a three dimensional shape? Give an example of why that would be a good measurement to know.
Answers
Answer:
Step-by-step explanation:
Width, Length, and Height being combine it by multiplying.
For a regular prism (where all the sides are the same) calculate the area of one of the sides and multiply by the total number of sides. For irregular prisms (with different sides) calculate the area of each side. Add your two answers together (ends × sides) to find the total surface area of the prism.
the complement of an angle is 57 degrees, what is the size of the angle?
Answers
Answer:
43 degreesStep-by-step explanation:
Find the product using the correct number of significant digits.
0.025 x 4.07 =
Answers
Answer: 0.10175
Step-by-step explanation:
First, bring the decimal points to the right for both numbers, to be a total of 5 decimal points to the right. Then, with the numbers 25 and 407, multiply them, and we get 10175. Then, we must bring the 5 decimal points back, and we end up with 0.10175.
Answer: 0.10
Step-by-step explanation:
on time4llearning
28. solve the 1-dimensional heat equation probleməu/ət = 2 ə^2u/əx^2u(0,t) = u (5,t) = 0, fro t> 0u(x,0) = f(x) = -4sin (πx) + 3sin (2πx), for 0 < x < 5
Answers
The solution to the 1-dimensional heat equation problem with the given initial and boundary conditions is \(u(x, t) = \sum_{n=1}^\infty \frac{(-1)^n}{n\pi} \sin\left(\frac{n\pi x}{5}\right) e^{-(n\pi)^2 \frac{2t}{25}}\).
We are given the one-dimensional heat equation:
\(\frac{\partial u}{\partial t} = 2 \frac{\partial^2 u}{\partial x^2}\)
We need to find the solution u(x, t) subject to the initial condition u(x, 0) = f(x) and boundary conditions u(0, t) = u(5, t) = 0 for t > 0.
To solve this problem, we use separation of variables:
u(x, t) = X(x)T(t)
Substituting this into the heat equation and dividing by u(x, t), we obtain:
\(\frac{1}{T(t)}\frac{dT}{dt} = \frac{2}{X(x)}\frac{d^2X}{dx^2}\)
Both sides are equal to a constant, which we denote by -λ². We then obtain two ordinary differential equations:
\(\frac{d^2X}{dx^2} + \lambda^2X = 0\)
\(\frac{1}{T} \frac{dT}{dt} = -\frac{\lambda^2}{2}\)
The general solution to the first equation is:
\(X(x) = A \sin\left(\frac{\pi x}{L}\right) + B \cos\left(\frac{\pi x}{L}\right)\)
where L = 5 is the length of the interval and A, B are constants determined by the boundary conditions.
The second equation has the solution:
\(T(t) = Ce^{-\lambda^2t/2}\)
where C is a constant determined by the initial condition.
The general solution to the heat equation is then:
\(u(x,t)=\sum\limits_{n=1}^{\infty}\left(A_n\sin\left(\frac{n\pi x}{5}\right) + B_n\cos\left(\frac{n\pi x}{5}\right)\right)e^{-\frac{n^2\pi^2t}{5^2}}\)
where the sum is taken over all positive integers n.
Using the initial condition, we can determine the coefficients A_n and B_n as:
A_n = \((-1)^n \frac{(4n\pi\sin(n\pi) - 3\sin(2n\pi))}{n^3\pi^3}\)
B_n = 0
Therefore, the solution to the given problem is:
\(u(x, t) = \sum_{n=1}^\infty \frac{(-1)^n}{n\pi} \sin\left(\frac{n\pi x}{5}\right) e^{-(n\pi)^2 \frac{2t}{25}}\)
Learn more about heat equation: https://brainly.com/question/13195935
#SPJ11
The value where the histogram balances when supported at that point is called ____.
Answers
The value where the histogram balances when supported at that point is called the mode of the distribution.
The mode of distribution is the value that appears most frequently in the data set. It is often used as a measure of central tendency, along with the mean and median. The mode is especially useful when dealing with categorical or discrete data, where the possible values are limited and well-defined.
For example, the mode of a list of test scores might be the score that occurs most frequently, indicating the most common level of performance. In a histogram, the mode is the value where the distribution is highest, or where the histogram balances when supported at that point.
Learn more about histograms:
https://brainly.com/question/2962546
#SPJ4
please Help me With these last 4 problems!! and show you workkkk

Answers

She must determine height of the clock tower using a 1.5 m transit instrument (calculations are done 1.5 m above level ground) from a distance 100 m from the tower she found the angle of elevation to be 19 degrees. How high is the clock tower from 1 decimal place?
Answers
Step-by-step explanation:
We can use trigonometry to solve this problem. Let's draw a diagram:
```
A - observer (1.5 m above ground)
B - base of the clock tower
C - top of the clock tower
D - intersection of AB and the horizontal ground
E - point on the ground directly below C
C
|
|
|
|
| x
|
|
|
-------------
|
|
|
|
|
|
|
|
|
B
|
|
|
|
|
|
|
|
|
|
|
A
```
We want to find the height of the clock tower, which is CE. We have the angle of elevation ACD, which is 19 degrees, and the distance AB, which is 100 m. We can use tangent to find CE:
tan(ACD) = CE / AB
tan(19) = CE / 100
CE = 100 * tan(19)
CE ≈ 34.5 m (rounded to 1 decimal place)
Therefore, the height of the clock tower is approximately 34.5 m.
For triangle TUV let angle V = 90°.
If angle U = 47° and TU = 13.28, what is the measure of TV

Answers
Answer:
TV = 9.71
Step-by-step explanation:
sin 47° = TV/13.28
0.7314 = TV/13.28
TV = 9.71
using the p-value rule for a population proportion or mean, if the level of significance is less than the p-value, the null hypothesis is rejected. group startstrue or false
Answers
The given statement "Using p-value rule for a population proportion or mean, if the level of significance is less than p-value, null hypothesis is rejected." is True because the hypothesis is rejected in this case.
In hypothesis testing, the p-value is the probability of observing a test statistic as extreme as, or more extreme than, the observed test statistic, assuming that the null hypothesis is true. The level of significance, denoted by alpha, is the maximum probability of rejecting the null hypothesis when it is actually true.
If the p-value is less than the level of significance, it means that the observed test statistic is unlikely to have occurred by chance alone, assuming the null hypothesis is true. Therefore, we reject the null hypothesis in favor of the alternative hypothesis at the given level of significance.
For example, suppose we are testing the hypothesis that the population mean is equal to a certain value. If the p-value is 0.02 and the level of significance is 0.05, we would reject the null hypothesis because the p-value is less than the level of significance.
This means that there is strong evidence against the null hypothesis and we can conclude that the population mean is likely different from the hypothesized value.
In summary, if the level of significance is less than the p-value, we reject the null hypothesis in favor of the alternative hypothesis at the given level of significance.
To learn more about p-value click on,
https://brainly.com/question/14619443
#SPJ4
What is the equation of a line, in point-slope form, that passes through (-8, 1) and has a slope of 5/6?
Answers
Answer:
y-1=\(\frac{5}{6}\)(x+8)
Step-by-step explanation:
1. y-y1=m(x-x1) (point slope form)
2. y1 is the y of your given point and x1 is the x of your given point
3. m is the slope
IXL percent of change
Answers
Answer:
What? I think you forgot to attach the picture.
a fair cube has 2 red sides, 2 blue sides, and 2 green sides what is the probability of rolling red or blue
Answers
This website is helpful hope this helped
https://studyandanswers.com/mathematics/question15393270#
The probability of rolling a red or blue on the fair cube is P = 2/3 = 0.67
What is Probability?The probability that an event will occur is measured by the ratio of favorable examples to the total number of situations possible
Probability = number of desirable outcomes / total number of possible outcomes
The value of probability lies between 0 and 1
Given data ,
Let the probability of rolling a red or blue on the fair cube is P
Now , there are a total of 6 sides on the fair cube, with 2 red sides, 2 blue sides, and 2 green sides.
The probability of rolling a red or blue side can be found by dividing the number of red or blue sides by the total number of sides.
The number of red or blue sides is 2 + 2 = 4, since there are 2 red sides and 2 blue sides.
The total number of sides is 6.
Therefore, the probability of rolling a red or blue side is:
P(red or blue) = (number of red or blue sides) / (total number of sides) = 4/6 = 2/3
So the probability of rolling a red or blue side on the fair cube is 2/3 or approximately 0.67
Hence , the probability is 2/3
To learn more about probability click :
https://brainly.com/question/17089724
#SPJ3
A roller coaster train with 6 passenger cars and the front decoration has a mass of 3,500kg. when the train has the front decoration and only 4 passenger cars, it has a mass of 2,400kg.
what is the mass of the decoration and of each passenger car?
Answers
The mass of the decoration is 200 kg and for each passenger car is 550 kg
How to determine the mass of the decoration and of each passenger car?From the question, we have the following parameters that can be used in our computation:
6 passenger cars and the front decoration = 3,500kg4 passenger cars and the front decoration = 2,400kgThese can be represented as
(6, 3500) and (4, 2400)
The slope of the above points represent the mass of each passenger car
This is calculated as
Slope = Difference in mass/Difference in number of cars
So, we have
Slope = (3500 - 2400)/(6 - 4)
Evaluate
Slope = 550
When there are no passenger cars in the train, we have
(0, Mass of decoration)
Using the slope formula, we have
Slope = (Mass of decoration - 3500)/(0 - 6)
So, we have
Slope = (Mass of decoration - 3500)/(-6)
This gives
(Mass of decoration - 3500)/(-6) = 550
Cross multiply
Mass of decoration - 3500 = -3300
Add 3500 to both sides
Mass of decoration = 200
Hence, the mass of decoration is 200 kg
Read more about slope at
https://brainly.com/question/29135291
#SPJ1
Write an expression for the total volume of the building
Answers
The expression for the total volume of the building is V = L × W × H.
Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
To write an expression for the total volume of a building, we'll need to consider the dimensions of the building: length (L), width (W), and height (H). The volume of a rectangular building can be calculated using the formula:
Total Volume (V) = Length (L) × Width (W) × Height (H)
So, the expression for the total volume of the building is V = L × W × H.
Learn more about volume,
https://brainly.com/question/27710307
#SPJ11
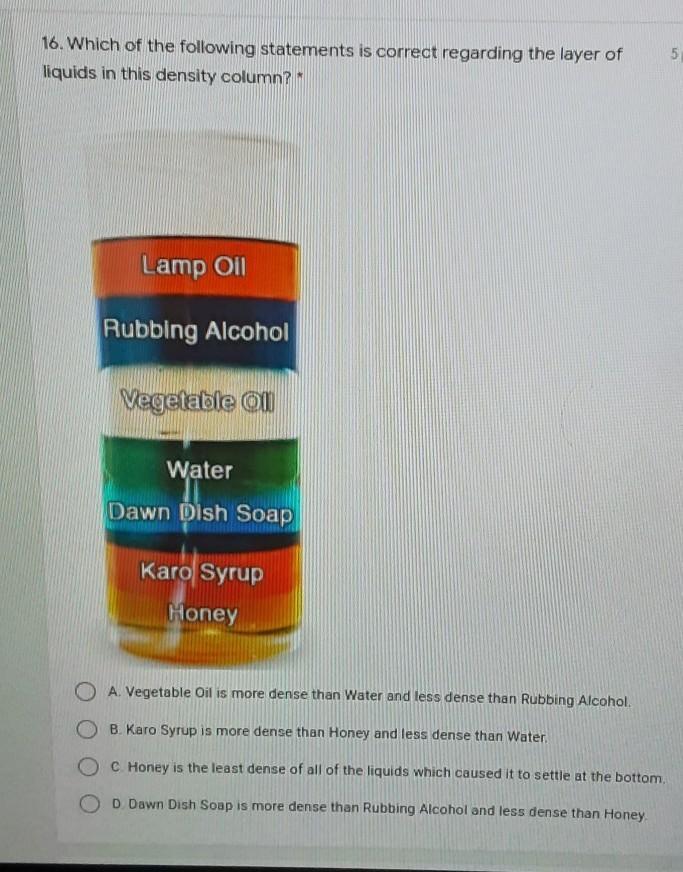
Question 10 of 25
The polynomial (x-2) is a factor of the polynomial 5x² - 6x +4.
O A. True
OB. False
Answers
Answer:
B. False
Step-by-step explanation:
5x² - 6x + 4 | 5 × 4 = 20
Can't factor it normally
√b² - 4ac
-b ± ---------------
2a
√(-6)² - 4(5)(4)
-(-6) ± ---------------
2(5)
√36 - 80
6 ± ---------------
10
6 ± √-44
---------------
10
6 ± √-4 × 11
---------------
10
6 ± 2i√11
---------------
10
The answer is actually
3 ± i√11
---------------
5
I hope this helps!
Answer:
B. False
Step-by-step explanation:
You want to know if (x -2) is a factor of 5x² -6x +4.
RemainderThere are a couple of ways you can determine whether (x -2) is a factor. One is to look at the polynomial value at x=2:
5x² -6x +4 = (5x -6)x +4 = (5(2) -6)(2) +4 = 4(2) +4 = 12
The value is not 0, so (x -2) is not a factor.
Other factorAnother way to tell is to determine what the other factor would be.
The product of roots is the ratio c/a = 4/5 in the polynomial. If 2 is a root, then (4/5)/2 = 2/5 is the other root. That would mean the factorization of the polynomial is ...
(5x -2)(x -2) = 5x² -12x +4 . . . . . . not the same polynomial
The polynomial 5x² -6x +4 does not have a factor (x -2).
GraphThe graph of the polynomial has no x-intercepts, so (x -2) cannot be a factor.
Please show all work and not just the answers. Please help ASAP!!!!!

Answers
9514 1404 393
Answer:
a) x = 14
b) NP = 2 2/9; NL = 2 7/9
Step-by-step explanation:
a) The similarity statement tells you that angle P and angle L have the same measure:
angle L = angle P
3x +18 = 60
x + 6 = 20 . . . . . divide by 3
x = 14 . . . . . . . . . subtract 6
__
b) The proportional segments are ...
PN/NQ = LN/NM
y/3.2 = (5 -y)/4
5y = 4(5 -y) . . . . . multiply by 16
9y = 20 . . . . . . . . add 4y
y = 20/9 = NP
5 -y = (45 -20)/9 = 25/9 = NL
Something times 3=-180
Answers
Answer:
60
Step-by-step explanation:
180 div 3
Answer:
60
Step-by-step explanation:
180/3
Given that the slope of the graphed linear function is -3, which formula could represent the function?
es -
A)
y = -3x + 4
B)
y = -3(x + 4)
y = -3x - 4
D)
y = -3(x - 4)
Answers
Answer: y= -3(x+4)
Step-by-step explanation:
pls help I’ll give BRAINLIEST
A conditional statement is shown.
"If two angles of a triangle are congruent, then it is an isosceles triangle."
Which figure represents a counterexample to this conditional statement?
A. Acute Triangle
B. Obtuse Triangle
C. Equilateral Triangle
D. Scalene Triangle
Answers
Answer:
Step-by-step explanation:
B.
The figure that represents a counterexample to the given conditional statement is option D, a Scalene Triangle.
Given that a conditional statement,
"If two angles of a triangle are congruent, then it is an isosceles triangle."
We need to determine the counterexample to this conditional statement,
A counterexample is an example that disproves a statement. In this case, if we can find a triangle where two angles are congruent but the triangle is not isosceles, it would serve as a counterexample to the given conditional statement.
A scalene triangle is a triangle where all three sides and angles are different.
If we consider a scalene triangle where two angles are congruent, it will violate the given conditional statement because it is not an isosceles triangle.
Therefore, a scalene triangle is the correct choice for a counterexample.
Learn more about conditional statement, click;
https://brainly.com/question/30612633
#SPJ4
NO EXPLANATION JUST ANSWER!

Answers
Answer: 1456 square yds
Step-by-step explanation: Please mark brainliest and give thanks!
Answer:728
Step-by-step explanation:
V=abc=19*14*c=266c=3724
c=14
S=(19c+14c+14*19)=33c+266=33*14+266=728
Use five iterations of the Newton's method to minimize the following functions e^(0.2x) - (x + 3)² – 0.01x⁴. Take the initial point as x^(0) = 0.
Answers
By applying Newton's method five times with an initial point of x^(0) = 0, we minimize the function e^(0.2x) - (x + 3)² - 0.01x⁴. The final approximation for the minimum is x ≈ -2.4505.
Newton's method is an iterative optimization technique used to find the minimum or maximum of a function. To apply it, we start with an initial point and iteratively update it using the derivative of the function until convergence is achieved.
In this case, we want to minimize the function f(x) = e^(0.2x) - (x + 3)² - 0.01x⁴. We begin with an initial point x^(0) = 0. First, we compute the derivative of f(x) with respect to x, which is f'(x) = 0.2e^(0.2x) - 2(x + 3) - 0.04x³.
Using Newton's method, we update our initial point as follows:
x^(1) = x^(0) - f(x^(0))/f'(x^(0))
x^(1) = 0 - (e^(0.20) - (0 + 3)² - 0.010⁴) / (0.2e^(0.20) - 2(0 + 3) - 0.040³)
x^(1) ≈ -1.2857
We repeat this process for four more iterations, plugging the updated x values into the formula above until convergence. After five iterations, we find that x ≈ -2.4505, which is the final approximation for the minimum of the given function.
Learn more about five iterations of Newton :
https://brainly.com/question/31377097
#SPJ11
What is the value of the expression −3 1/3÷(−2.4) ?
Answers
Answer:
First, we need to convert the mixed number −3 1/3 to a fraction. −3 1/3 = −(3 + 1/3) = −(10/3).
Now, we can divide the fraction by the decimal. −(10/3) ÷ (-2.4) = −(10/3) ÷ (-24/10) = −(10/3) x (10/-24) = 10/-7.2 = -1.388888889.
Therefore, the value of the expression is −1.388888889.
Step-by-step explanation:
1. Convert the mixed number to a fraction.
```
-3 1/3 = -(3 + 1/3) = -(10/3)
```
2. Multiply the numerator and denominator of the fraction by -1.
```
-(10/3) = (-1)(10/3) = -10/3
```
3. Divide the numerator and denominator of the fraction by -24.
```
-10/3 = (-10/3) ÷ (-24/10) = 10/-7.2 = -1.388888889
```
Therefore, the value of the expression is −1.388888889.
Here is a visual representation of the steps:
```
-3 1/3 ÷ (-2.4)
= -(10/3) ÷ (-24/10)
= -(10/3) x (10/-24)
= 10/-7.2
= -1.388888889
```
Solve:
3(x + 4) - 5(x - 1) < 5
A ....x<-3
B..... X > -3
C. ......x > 1
D..... x<6
E...... x > 6
Answers
Answer:
х > 6
Step-by-step explanation:
Раскроем скобки:
3x + 12 - 5x + 5 < 5
Приведём подобные. Всё, что с х, перенесем в левую часть:
-2x < -12
Разделим на (-2). Поменяем знак:
x > 6
- 2 2 a 2 Increasing: Increasing Decreasing: Decreasing: Range: Range:
Answers
the graph increases when the values in y are increasing
we must mention the part of x where the function increases
so
Increassing:
\((-\infty,1)\)because the graph is increasing from a very small number to the number 1
the graph decreases when the values in and are less and less
we must mention the part of x where the function decreasing
so
Decreasing:
\((1,\infty)\)because the graph starts to decrease from the number 1 to a very large number
the range is the part of y that the graph uses, from the lowest point to the highest
Range:
\((-\infty,2\rbrack\)because the smallest number is a very small number and the largest number that takes in y is 2

Liz flips a coin 60 times. The coin lands heads up 36 times and tails up 24 times. Complete each statement.

Answers
Answer: 58.33%
Step-by-step explanation:
So, Liz flipped the coin a total of 60 times
Let this be the denominator.
Probability of coin landing up: 35/60
Probability of coin landing down: 24/60
We need the probability of the coin landing up.
So, convert 35/60 into a percentage
To find percentage, we need to find an equivalent fraction with denominator 100. Multiply both numerator & denominator by 1003560 × 100100= (35 × 10060) × 1100 = 58.33/100
So, the probability is 58.33%
A survey was given to a random sample of 400 residents of a town to determine whether they support a new plan to raise taxes in order to increase education spending. Of those surveyed, 168 respondents said they were in favor of the plan. Determine a 95% confidence interval for the proportion of people who favor the tax plan, rounding values to the nearest thousandth.
Answers
The standard error of the sample proportion is sqrt[(0.42)(0.58)/400] = 0.032.
Using a 95% confidence level, the critical value is 1.96.
The margin of error is 1.96 * 0.032 = 0.063.
The 95% confidence interval is 0.42 ± 0.063, which is (0.357, 0.483).
Therefore, we can be 95% confident that the true proportion of people who favor the tax plan is between 0.357 and 0.483.
Really need this, click on photo if neccessary