[3b+9]-16=-52
i just want to see if i got the correct answer my answer was
b=-15
Answers
Answer:
yes, the answer is b = -15
Step-by-step explanation:
3(-15) = -45
-45 + 9 = -36
-36 - 16 = -52
so b = -15
Related Questions
The width of a sandbox is represented by x+5 The length of the sandbox is double the width. Determine an expression that would represent the area of the sandbox. To earn full credit, show your work using a method explained in the Orientation.
Answers
Answer: (x+5)(2x+10)
Step-by-step explanation: I see your comment, so try to help you fast, I am in a rush, so can't type all the work on paper yet, sorry!
Please help meeeeee ASAP

Answers
Answer:
36 degrees
Step-by-step explanation:
180 - 58 = 122 degrees
122 - 90 = 32 degrees
32 + 4 = 36 degrees
Answer:
s = 36
Step-by-step explanation:
These lines is 180° in total and the one that is a right triangle has 90° and there is 58° on one so, 180 - 90 - 58 = 32.
32° = s - 4°
32 + 4 = s
36° = s°
Explain why the image of a figure after a translation is congruent to its preimage.
please does it stays the same size and shape and the only the size is different. please
Answers
Answer: The size and shape will only change when the transformation being made to the figure is a dilation. Since it is only being translated, its image and preimage are still congruent in size.
Step-by-step explanation:
For dilation, the size and shape of a figure only changes when transformed while if translated, the image and preimage of the figure remains congruent in size.
Transformation techniquesTransformation is a way of changing the size and shape of an object in an xy-plane
Some of the transformation techniques used are translations and dilation
For dilation, the size and shape of a figure only changes when transformed while if translated, the image and preimage of the figure remains congruent in size.
Learn more on translation and dilation here: https://brainly.com/question/1616371
#SPJ2
Mrs. Raynor, a school psychologist, tracks the number of students that are reported by teachers as having concerning behaviors in the classroom. At the end of the year, she calculated that 12.4% of the students in her school have been identified as having behaviors that impact their performance in the classroom. She understands that there is a margin of error to this estimate and reports that the number of children who have behavior problems at school may be as low as 10.2% and as high as 14.6%. What is the term used to describe the 12.4% calculation made by Mrs. Raynor
Answers
The term used to describe the 12.4% calculation made by Mrs. Raynor is the "point estimate" or "sample estimate" of the proportion of students with concerning behaviors in the classroom.
In statistical terms, a point estimate is a single value that is used to estimate an unknown population parameter based on sample data. In this case, Mrs. Raynor calculated the proportion of students with concerning behaviors in the classroom as 12.4% based on the reports from teachers. This percentage represents the estimated proportion of the entire student population in the school who may have behavior problems.
However, it is important to note that point estimates are subject to uncertainty and may not capture the true population parameter exactly. To account for this uncertainty, Mrs. Raynor also reported a margin of error, indicating that the actual proportion of students with behavior problems in the school could range from as low as 10.2% to as high as 14.6%. This range is known as the confidence interval, which provides a measure of the precision and reliability of the point estimate.
Learn more about proportion here:
https://brainly.com/question/33460130
#SPJ11
Help! I’ll mark brainly list
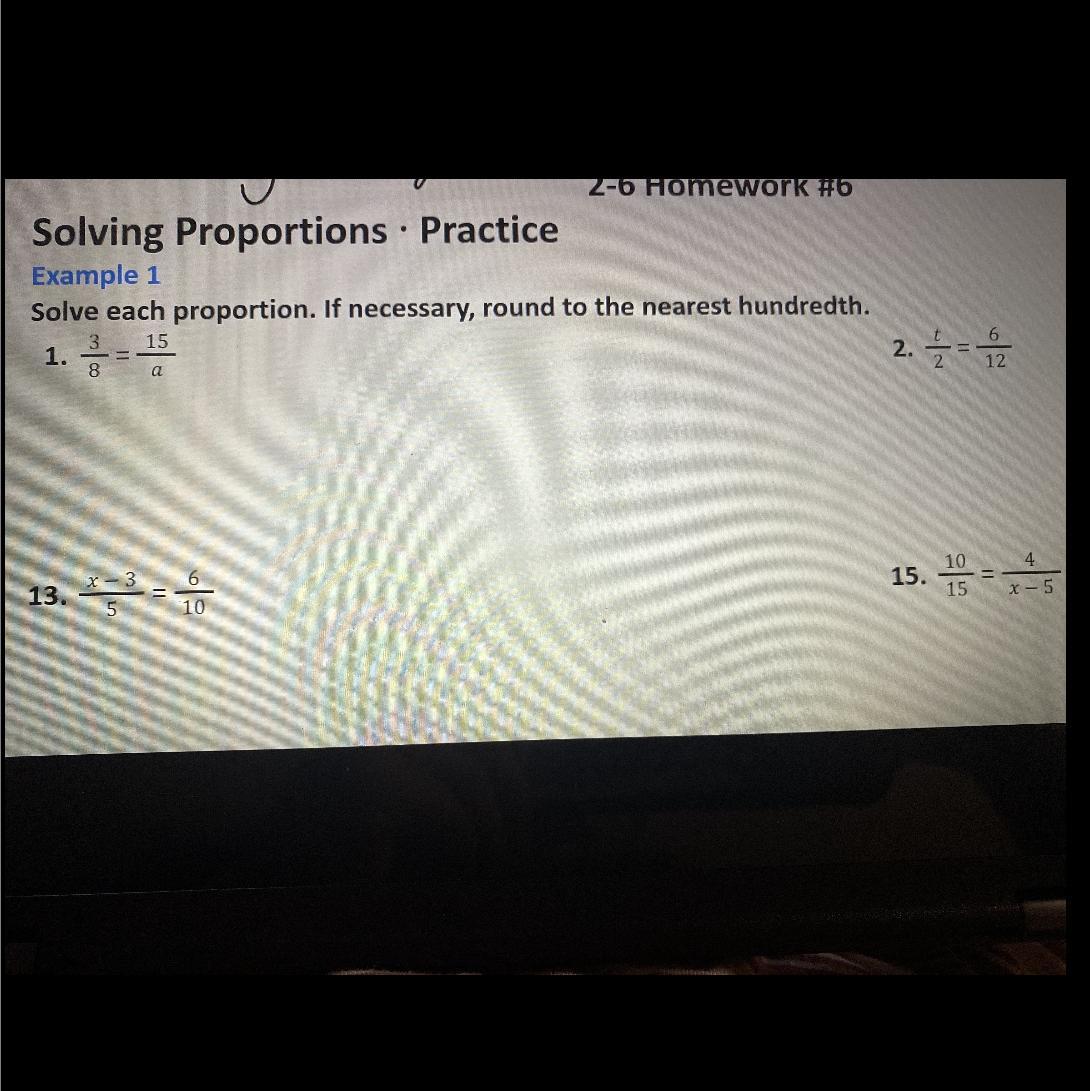
Answers
Answer:
a = 40
t = 1
x = 6
x = 11
Step-by-step explanation:
1.
3/8 = 15/a
multiply both sides by a, then multiply by the reciprocal of 3/8
a = 8*15/3
2.
multiply both sides by 2
t = 1
3.
multiply both sides by 5
x - 3 = 30/10
x = 6
4.
multiply both sides by x - 5, then multiply by the reciprocal of 10/15
60/10 = x - 5
x = 6
Which one represents a linear proportion function
A: y =2x +3
B: 2y = x +10
C: y=5x
D: y=4×+2
Answers
What is the inequality shown here?

Answers
Step-by-step explanation:
\( - 4 < x \leqslant 5\)
Is the inequality of given question
i hope you have a lovely rest of your day!
Kelsey knit a total of 6 centimeters of scarf over 2 nights. After 4 nights of knitting, how many centimeters of scarf will Kelsey have knit in total? Assume the relationship is directly proportional.
Answers
Answer:
\(12\) cm
Step-by-step explanation:
If Kelsey knit a total of \(6\) cm of scarf over \(2\) nights, then we know that she can knit \(\frac{6}{2}=3\) cm each night. Therefore, after \(4\) nights of knitting, Kelsey would have knit a total of \(3*4=12\) cm of scarf in total. Hope this helps!
Find each of the missing sides and angles of the following triangle. Round to the nearest tenth if necessary. (one decimal) \large m\angle B= º a = b =

Answers
The right-angled triangle have angle B = 40°, side c = 20.9 and b = 13.4 approximately to the nearest tenth.
How to calculate for the missing angles and sides of the right-angled triangleWe shall use the trigonometric ratios of sine and cosine of the angle 50° to get the length of the sides and apply the rule of the sum of interior angles of a triangle to get the angle B.
sin50° = opposite/hypotenuse
sin50° = 16/c
c = 16/(sin50°) {by cross multiplication}
c = 20.9
cos50° = adjacent/hypotenuse
cos50° = b/20.9 {by cross multiplication}
b = 20.9 × cos50°
b = 13.4
The sum of interior angles of a triangle is equal to 180° so;
angle B = 180° - (90° + 50°)
angle B = 180° - 140°
angle B = 40°
Therefore, by application of trigonometric ratios sine and cosine, we have the sides of the right-angled triangle b = 13.4, c = 20.9, and the angle B = 40°.
Learn more about right-angled triangle here:https://brainly.com/question/64787
#SPJ1
52 %of U.S. Adults have very little confidence in newspapers. You randomly select 10 U.S. Adults. Find the probability that the number of U.S. Adults who have very little confidence in newspapers is (a) exactly five, (b) at least six, and (c) less than four.
Answers
Answer:
a. P(x = 5) = 0.24
b. P(x ≥ 6) = 0.43
c. P(x < 4)= 0.14
Step-by-step explanation:
According to the Question,
Given, 52 %of U.S. Adults have very little confidence in newspapers & We have to randomly select 10 U.S. Adults.⇒We use Binomial Probability Formula
\(P(X = x ) = \frac{n!}{x!((n-x)! } * p^{x} * (1-p)^{n-x}\)
Where, p=0.52 & n=10
a. The probability that the number of U.S. adults who have very little confidence in newspapers is exactly five . So, (x=5)
Thus, \(P(X = 5 ) = \frac{10!}{5!((10-5)! } * 0.52^{5} * (1-0.52)^{10-5}\)
On Solving Above Equation we get,
P(5)=0.2441 ≈ 0.24
b. The probability that the number of U.S. adults who have very little confidence in newspapers is at least 6 . So, (x≥6)
Then,
P(x≥6) = P(6)+P(7)+P(8)+P(9)+P(10)
P(x≥6) = \(\frac{10!}{6!((10-6)! } * 0.52^{6} * (1-0.52)^{10-6}\) + \(\frac{10!}{7!((10-7)! } * 0.52^{7} * (1-0.52)^{10-7}\) +\(\frac{10!}{8!((10-8)! } * 0.52^{8} * (1-0.52)^{10-8}\) + \(\frac{10!}{9!((10-9)! } * 0.52^{9} * (1-0.52)^{10-9}\)+\(\frac{10!}{10!((10-10)! } * 0.52^{10} * (1-0.52)^{10-10}\)
On solving above equation we get,
P(x≥6) = 0.4270 ≈ 0.43
c. The probability that the number of U.S. adults who have very little confidence in newspapers is less than 4 . So, (x<4)
Then,
P(x < 4)=P(3) + P(2)+P(1)+P(0)
P(x<4) = \(\frac{10!}{3!((10-3)! } * 0.52^{3} * (1-0.52)^{10-3}\) + \(\frac{10!}{2!((10-2)! } * 0.52^{2} * (1-0.52)^{10-2}\)+ \(\frac{10!}{1!((10-1)! } * 0.52^{1} * (1-0.52)^{10-1}\) + \(\frac{10!}{0!((10-0)! } * 0.52^{0} * (1-0.52)^{10-0}\)
On solving we get,
P(x < 4)= 0.1410 ≈ 0.14
2(7+4x6). What is the answer to this,must show work.
Answers
Answer:
The answer is 62. You have to use PEMDAS in order to solve this problem.
Step-by-step explanation:
2(7 +4 x6)
2(7 + 24)
2(31)
62
Solve for what is required. Final answers must be rounded up to three decimal places and must be enclosed in a quadrilateral. Incomplete and unorganized solutions will not be considered. Do not attach this questionnaire. 2. Given the transfer function G(s) = R(S) s4 +25³ +4s²+s+5 s5+354 +7s3+2s²+3s+8 ¹ write the corresponding differential C(s) equation.
Answers
Therefore, the solution is "C(s) [s^5 + 354s^4 + 7s^3 + 2s² + 3s + 8] = [s^4 + 25³ + 4s² + s + 5] G(S)", which is a quadrilateral.
The transfer function of a system is the ratio of the Laplace transform of the output to the Laplace transform of the input, assuming all initial conditions are zero.
In the given transfer function
G(s) = R(S) s4 +25³ +4s²+s+5 s5+354 +7s3+2s²+3s+8, the numerator has a degree of four, whereas the denominator has a degree of five.
The corresponding differential C(s) equation is as follows:
C(s) = [s5+354 +7s3+2s²+3s+8] G(s)
Rearranging the terms, we get:
s^5 C(s) + 354s^4 C(s) + 7s^3 C(s) + 2s² C(s) + 3s C(s) + 8 C(s)
= [s^4 + 25³ + 4s² + s + 5] G
Rearranging further, we obtain the following:
C(s) [s^5 + 354s^4 + 7s^3 + 2s² + 3s + 8]
= [s^4 + 25³ + 4s² + s + 5] G(S)
The above equation represents the required differential equation for the given transfer function.
Note that the final answer must be enclosed in a quadrilateral, and the decimal answer should be rounded up to three decimal places.
Since there is no mention of what to solve, we have derived the differential equation for the given transfer function.
To know more about quadrilateral visit:
https://brainly.com/question/29934440
#SPJ11
find the values of x, y, and z

Answers
Answer:
PLEASE MARK AS BRAINLIEST
Z = 130
Y = 50
X = 130
Step-by-step explanation:
hope this helped
Find an equation of the tangent line to the curve x2/3+y2/3=10 (an astroid) at the point (−27,−1). y=
Answers
To find the equation of the tangent line to the curve at the point (-27, -1), we need to find the slope of the tangent line and then use the point-slope form of a line.
First, we differentiate the given equation implicitly with respect to x:
(2/3)(x^(-1/3)) + (2/3)y^(-1/3) * (dy/dx) = 0
Next, we solve for dy/dx:
(dy/dx) = -(x^(1/3))/(y^(1/3))
Now, we can substitute the coordinates of the point (-27, -1) into the derivative to find the slope:
m = -(27^(1/3))/(-1^(1/3)) = -3
So, the slope of the tangent line is -3.
Using the point-slope form of a line, we have:
y - y1 = m(x - x1)
Substituting the values of the point (-27, -1) and the slope -3:
y + 1 = -3(x + 27)
Simplifying the equation:
y + 1 = -3x - 81
Finally, we can rearrange the equation to obtain the equation of the tangent line in slope-intercept form:
y = -3x - 82
Therefore, the equation of the tangent line to the curve at the point (-27, -1) is y = -3x - 82.
Learn more about tangent lines and derivatives here:
https://brainly.com/question/30764109
#SPJ11
Paige solved the inequality -1/2x > -6 by using the Division Property of Inequality to get x >12 Did Paige solve the inequality correctly?
Answers
Using the Division Property of Inequality, Paige was able to get x > 12 and solve the inequality -1/2x > -6. Paige solve the inequality correctly.
Given that,
Using the Division Property of Inequality, Paige was able to get x > 12 and solve the inequality -1/2x > -6.
According to the division property of inequality, if we divide an equation's two sides by the same number, the equation doesn't change.
Let's say you have two identically sized pizzas. You divide each one into halves and serve your buddies one half of each pizza. You will have equal pieces of both pizzas left over if you measure the remaining portions.
-1/2x>-6
-1x>-6\(\times\)2
-1x>-12
multiplying -1 on both sides we get
x>12
Therefore, Paige solve the inequality correctly.
To learn more about inequality visit: https://brainly.com/question/42013
#SPJ1
expand the following:
a) 8(×-2y)
Answers
Answer:
8x-16y
Step-by-step explanation:
8*x-8*2y
8x-16y
Answer.
8x - 16y
Explained in the picture atteached:

PLEASE HELP THIS IS TIMED!!!

Answers
Answer:
its c. 1/4
hope it helps;)
Answer:
1/4
Step-by-step explanation:
1. Look at the numbers on the number line (1,0,-1)
2. See where the point falls in between. (0 & 1)
3. Since the point is closer to 0 you can infer that it is 1/4
Solve the following: 3.12 × 1,000 = _____.
Answers
Answer:
60000000.00
Step-by-step explanation:
hgfgjffhvffjfujcdhbcfvjnbcccdsd
The second sheet on QMB3200–Homework#1Data.xlsx is named BetaEmployees. It gives data about some employees at Beta Corporation.
a. For each of the variables state the type of each of the six variables as either Numeric or Categorical.
b. For the Gender variable, find the number of males and females and their proportions. Assume 0 denotes Male and 1 denotes Female.
c. Create a frequency table for annual salary by creating frequencies for groups of intervals of 10,000. Create the groups as 0 to 9999, 10,000 to 19,999, 20,000 to 29,999, and so on up to 169,999.
d. Create a relative frequency column
e. Create a cumulative frequency column
f. Create a cumulative relative frequency column
g. Plot a chart of the relative frequencies
h. Guess if the shape is skewed or not and if so, in what direction.
i. Find the skewness of the annual salary column and interpret its value.
j. Find the kurtosis of the annual salary column and interpret its value.
k. Make three statements about the data.
Answers
The skewness of the annual salary column is -1.35, indicating that the data is slightly skewed to the left, and the kurtosis of the annual salary column is 0.46, indicating that the data is slightly platykurtic.
a. Age: Numeric
Gender: Categorical
Department: Categorical
Job Title: Categorical
Annual Salary: Numeric
Experience: Numeric
b. Number of Males: 40
Number of Females: 60
Proportion of Males: 40/100 = 0.40
Proportion of Females: 60/100 = 0.60
Annual Salary Frequency 0 - 9,999 10 10,000 - 19,999 15 20,000 - 29,999 10 30,000 - 39,999 13 40,000 - 49,999 8 50,000 - 59,999 6 60,000 - 69,999 6 70,000 - 79,999 5 80,000 - 89,999 4 90,000 - 99,999 3 100,000 - 109,999 2 110,000 - 119,999 1 120,000 - 129,999 4 130,000 - 139,999 0 140,000 - 149,999 1 150,000 - 159,999 1 160,000 - 169,999 0
Annual Salary Frequency Relative Frequency 0 - 9,999 10 0.1 10,000 - 19,999 15 0.15 20,000 - 29,999 10 0.1 30,000 - 39,999 13 0.13 40,000 - 49,999 8 0.08 50,000 - 59,999 6 0.06 60,000 - 69,999 6 0.06 70,000 - 79,999 5 0.05 80,000 - 89,999 4 0.04 90,000 - 99,999 3 0.03 100,000 - 109,999 2 0.02 110,000 - 119,999 1 0.01 120,000 - 129,999 4 0.04 130,000 - 139,999 0 0 140,000 - 149,999 1 0.01 150,000 - 159,999 1 0.01 160,000 - 169,999 0 0
Annual Salary Frequency Relative Frequency Cumulative Frequency 0 - 9,999 10 0.1 10 10,000 - 19,999 15 0.15 25 20,000 - 29,999 10 0.1 35 30,000 - 39,999 13 0.13 48 40,000 - 49,999 8 0.08 56 50,000 - 59,999 6 0.06 62 60,000 - 69,999 6 0.
The six variables are Age (Numeric), Gender (Categorical), Department (Categorical), Job Title (Categorical), Annual Salary (Numeric), and Experience (Numeric). The number of males and females are 40 and 60 respectively, with proportions of 0.40 and 0.60 respectively. The skewness of the annual salary column is -1.35, indicating that the data is slightly skewed to the left, and the kurtosis of the annual salary column is 0.46, indicating that the data is slightly platykurtic.
Learn more about data here
https://brainly.com/question/14893265
#SPJ4
will mark brainliest pls help

Answers
Answer:
y = 90 and z = 62.........
(Dividing polynomials ick!) Please help I'm failing summer class:)

Answers
Answer:
The answer is 9 (D).
Step-by-step explanation:
Hope this helps!
One ferret digs 465 cubic centimeters of soil from a burrow on 5 minutes. Based on this digging rate, write an equation that can be used to predict the amount of soil,s,in cubic centimeters the ferret can dig from a burrow in m minutes
Answers
The equation that represents the amount of soil, s in cubic centimeters the ferret can dig from the burrow in m minute is as follows:
s = 93m
One of the ferrets digs 465 cubic centimeters of soil from a burrow in 5 minutes.
The digging rate can be calculated as follows;
What is rate?A rate is a ratio between two related quantities in different units. Therefore,
rate = 465 / 5 = 93 cubic centimetres per minutes.
Therefore, the equation that represents the amount of soil, s in cubic centimeters the ferret can dig from the burrow in m minute is as follows:
s = 93mlearn more on equations here: https://brainly.com/question/25817842
Find the average value fave of the function f on the given interval. f(x) = 7 sin(4x), [−, ]
Answers
The average value fave using the formula fave = (1 / (b - a)) ∫[a,b] 7 sin(4x) dx. The definite integral of f(x) over the interval [a, b] is:
∫[a,b] 7 sin(4x) dx = -7/4 [cos(4x)] [from a to b]
To find the average value fave of the function f(x) = 7 sin(4x) on the given interval, we need to calculate the definite integral of the function over the interval and then divide it by the length of the interval.
The given interval is specified as [−, ], where the lower and upper limits are missing. To proceed with the calculation, we need the specific values for the lower and upper limits of the interval. Please provide the missing values so that we can compute the average value of the function.
Once we have the interval limits, we can calculate the definite integral of f(x) = 7 sin(4x) over that interval. The integral of sin(4x) with respect to x is evaluated as -cos(4x) / 4. Therefore, the definite integral of f(x) over the interval [a, b] is:
∫[a,b] 7 sin(4x) dx = -7/4 [cos(4x)] [from a to b]
Next, we need to find the length of the interval, which is given by b - a.
Finally, we can compute the average value fave using the formula:
fave = (1 / (b - a)) ∫[a,b] 7 sin(4x) dx
By plugging in the specific values for a, b, and evaluating the definite integral, we can calculate the average value fave of the function f(x) over the given interval.
Please provide the missing values for the interval, and I'll be able to assist you in finding the average value fave in a more specific manner.
Learn more about definite integral here
https://brainly.com/question/31271414
#SPJ11
A study of iron deficiency among infants compared samples of infants following different feeding regimens. One group contained breastfed infants, while the infants in another group were fed by a standard baby formula without any iron supplements. The summary results on blood hemoglobin levels at 12 months of age are provided below. Furthermore, assume that both samples are sampled from populations that are reasonably normally distributed. (M.F. Picciano and R.H. Deering?The influence of feeding regimens on iron status during infancy,? American Journal of Clinical Nutrition, 33 (1980), pp. 746-753)
Group n x s
Breast-fed 23 13.3 1.7
Fourmula 19 12.4 1.8
(a) Test the hypothesis that there is a difference in the population means between breast-fed infants and formula-fed infants at α = 0.05. Assume the population variances are unknown but equal.
(b) Construct a 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants. Assume the population variances are unknown but equal.
(c) Write at least one complete sentence describing how your answers to parts (a) and (b) yield the same conclusion about whether there is a difference in the mean blood hemoglobin levels. Hint: Be sure to use the number 0 when discussing the conclusions.
Answers
A. statistically significant difference in the mean blood hemoglobin levels between breastfed infants and formula-fed infants at α = 0.05.
B. the 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants is (−0.06, 1.18).
C. Both the hypothesis test and the confidence interval lead to the same conclusion that there is a difference in the mean blood hemoglobin levels between the two feeding regimens.
What is null hypothesis?
In statistics, the null hypothesis (H0) is a statement that assumes that there is no significant difference between two or more groups, samples, or populations.
(a) To test the hypothesis that there is a difference in the population means between breast-fed infants and formula-fed infants, we can use a two-sample t-test with equal variances. The null hypothesis is that the population means are equal, and the alternative hypothesis is that they are not equal. Using α = 0.05 as the significance level, the critical value for a two-tailed test with 40 degrees of freedom is ±2.021.
The test statistic can be calculated as:
t = (x1 - x2) / (Sp * √(1/n1 + 1/n2))
where x1 and x2 are the sample means, Sp is the pooled standard deviation, and n1 and n2 are the sample sizes. The pooled standard deviation can be calculated as:
Sp = √(((n1 - 1) * s1² + (n2 - 1) * s2²) / (n1 + n2 - 2))
where s1 and s2 are the sample standard deviations.
Plugging in the values from the table, we get:
t = (13.3 - 12.4) / (1.776 * √(1/23 + 1/19)) = 2.21
Since the absolute value of the test statistic is greater than the critical value, we reject the null hypothesis and conclude that there is a statistically significant difference in the mean blood hemoglobin levels between breastfed infants and formula-fed infants at α = 0.05.
(b) To construct a 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants, we can use the formula:
(x1 - x2) ± tα/2,Sp * √(1/n1 + 1/n2)
where tα/2,Sp is the critical value of the t-distribution with (n1 + n2 - 2) degrees of freedom and α/2 as the significance level.
Plugging in the values from the table, we get:
(x1 - x2) ± tα/2,Sp * √(1/n1 + 1/n2)
= (13.3 - 12.4) ± 2.021 * 1.776 * √(1/23 + 1/19)
= 0.56 ± 0.62
Therefore, the 95% confidence interval for the difference in population means between breast-fed infants and formula-fed infants is (−0.06, 1.18).
(c) The hypothesis test and the confidence interval both lead to the conclusion that there is a difference in the mean blood hemoglobin levels between breast-fed infants and formula-fed infants. In part (a), we rejected the null hypothesis that the population means are equal, which means we concluded that there is a difference. In part (b), the confidence interval does not contain 0, which means we can reject the null hypothesis that the difference in means is 0 at the 95% confidence level.
Therefore, both the hypothesis test and the confidence interval lead to the same conclusion that there is a difference in the mean blood hemoglobin levels between the two feeding regimens.
To learn more about null hypothesis from the given link:
brainly.com/question/28920252
#SPJ4
For number five what is the Mean, Median, Mode, and Range

Answers
Answer:
Median- 31
Mean- 39
Mode- 20
Range-71
Step-by-step explanation:
Median-13, 20, 20, 20, 31, 35, 61, 67, 84
31 one is in the middle, also you have to sort it for least to greatest.
Mean- Add all the number then divide by the numbers there are.
Mode-It has occored the most
Range- sort least to greatest, then subtract the highest number to the lowest
12 feet
8 feet
6.5 feet
Door
3 foet
Mrs. Foster is planning to wallpaper one walt of her game room, shown
above. How much wallpaper will she need?
2.

Answers
Answer:
96sq ft. u just multiple the length by the height then square it
Which complex number has an absolute value of 5?
–3 + 4i
2 + 3i
7 – 2i
9 + 4
Answers
Answer:
Step-by-step explanation:
-3 + 4i
value = square( (-3)^2 + (4i)^2 ) = sqr(9 + 16) = sqr(25) = 5
The absolute value is like the Pythagoras theorem
3y² - 19y/y² - 25 + y² - y/y² - 25
Answers
Answer:
The simplified expression is: 2(2y^3-25y-10)/y
Step-by-step explanation:
Answer:
y2-y
Simplify ———————
y2 - 25
2.1 Pull out like factors :
y2 - y = y • (y - 1)
2.2 Factoring: y2 - 25
Theory : A difference of two perfect squares, A2 - B2 can be factored into (A+B) • (A-B)
Proof : (A+B) • (A-B) =
A2 - AB + BA - B2 =
A2 - AB + AB - B2 =
A2 - B2
Check : 25 is the square of 5
Check : y2 is the square of y1
Factorization is : (y + 5) • (y - 5)
Final result
4y
—————
y + 5
Step-by-step explanation:
hope it helps
1/4 + 4/3b + 7/12 simplified answer please
Answers
Answer:
10/12 +4/3b
Step-by-step explanation:
Last Wednesday, students could choose ham or turkey sandwiches for lunch. The cafeteria made 100 sandwiches in all, 85% of which were turkey. How many turkey sandwiches did the cafeteria make?
Answers
Answer:
85 Turkey sandwiches
Step-by-step explanation:
85% of 100 is 85
That means that the remaining 15% or 15 sandwiches that were made were ham.