40 is 60% of what number?

Answer:

y/x  Jonathan age divided by Jean's age

Step-by-step explanation:

hope this helps

Jonathon is [y/x] years older than Jean.

The general equation of a straight line is -

[y] = [m]x + [c]

where -

[m] → is slope of line which tells the unit rate of change of [y] with respect to [x].

[c] → is the y - intercept i.e. the point where the graph cuts the [y] axis.

The equation of a straight line can be also written to express proportional relationship as -

y = kx  {k is constant}

We have Jean is [x] years old and Jonathan is [y] years old

Assume that Jonathon is [m] years older than Jean. Then we can write -

y = mx

or

m = y/x

Therefore, Jonathon is [y/x] years older than Jean.

To solve more questions on direct proportionality, visit the link below-

brainly.com/question/20400984

#SPJ2

Answer:

b and c and e

Step-by-step explanation:

1+5=6

2=7-5

1/10•5=5/10=1/2

3/2d

DIFFERENTIATE W.R.T. D

3

2

​

≈0.666666667

Answer:

4

Step-by-step explanation:

hrhdhdjdjdjejehrhvhchhc

Answer:

Step-by-step explanation:

I think 4 AHH its hard UwU

After answering the provided question, we can state that Therefore, the parallelograms measure of angle C is 63°.

In Euclidean geometry, a parallelogram is a simple quadrilateral with two sets of parallel sides. A parallelogram is a type of quadrilateral in which both sets of opposite sides are parallel and equal. Parallelograms are classified into four types, three of which are unique. The four different shapes are parallelograms, squares, rectangles, and rhombuses. A quadrilateral is a parallelogram when it has two sets of parallel sides. The opposing sides and angles of a parallelogram are both the same length. The interior angles on the same side of the horizontal line are also angles. 360 degrees is the total number of interior angles.

Since ABCD is a parallelogram, opposite angles are congruent. Therefore,

m∠A = m∠C

13x - 41 = 6x + 15

7x = 56

x = 8

m∠C = 6(8) + 15 = 63

Therefore, the measure of angle C is 63°.

To know more about parallelograms visit:

https://brainly.com/question/29147156

#SPJ1

The length of one of the sides of the square base is 6 inches.

Let's denote the length of one of the sides of the square base by "s" and the height of the pyramid by "h". Then, the surface area of the pyramid can be expressed as:

Surface area = area of square base + sum of areas of four triangular faces

Surface area = s^2 + 4(1/2)(s)(h)

We know that the surface area is 116 in^2 and the sum of the areas of the four triangular faces is 80 in^2. So we can substitute these values into the equation:

116 = s^2 + 4(1/2)(s)(h)

80 = 4(1/2)(s)(h)

We can simplify the second equation to get:

20 = (1/2)(s)(h)

We can solve for h by substituting the value of (1/2)(s)(h) from the second equation into the first equation:

116 = s^2 + 4(20)

116 = s^2 + 80

s^2 = 36

s = 6

Therefore, the length of one of the sides of the square base is 6 inches.

Learn more about length below.

https://brainly.com/question/28322552

#SPJ1

Answer:

5.5

Step-by-step explanation:

by going off the total cost it should be 5.5 but if it's over c it should be y/5.5 x/8

Answer:

x^2 - 10x + 21

Step-by-step explanation:

Sum of zeros

= 7 + 3

= 10

Product of zeros

= 7 x 3

= 21

x^2 - ( sum of zeros )x + product of zeros

= x^2 - 10x + 21

The Quadratic polynomial is x^2 - 10x + 21.

if the zeroes of a quadratic polynomial are a and b, then the polynomial can be written as :

\( \boxed{{x}^{2} - (a + b)x + ab}\)

So,

\( \hookrightarrow \: {x}^{2} - (7 + 3)x + (7 \times 3)\)

\(\hookrightarrow \: {x}^{2} - 10x + 21\)

Answer:

One

Step-by-step explanation:

The equation 9x+7=8x+7 has only one solution. This can be seen by setting the two sides of the equation equal to each other and then solving for x.

First, we set the two sides equal to each other by canceling out the 7 on the right side of the equation:

9x+7 = 8x+7

Then, we move all of the terms that have an x on the same side of the equation, and all of the constant terms on the other side:

9x - 8x = 7 - 7

Next, we combine like terms on the left side of the equation:

x = 0

Finally, we solve for x to find the value of x that makes the equation true:

x = 0

Therefore, the only solution to the equation 9x+7=8x+7 is x=0.

Answer: y=10x+25

y=10(7)+25

=70+25

=$95

Step-by-step explanation:

Answer:

Below.

Step-by-step explanation:

Total payment = 1800 * 30 * 12 = 648,000.

Interest = 448,000.

Heather should have to pay total of $648,000 to the bank and Interest Heather will pay to the bank is $448,000.

Interest is the price you pay to borrow money or cost you charge to lend money. Interest can be calculated by total amount you paid after a specific time period minus the total amount you borrowed.

Heather borrowed $200,000 from a bank over a period of time 30 year.

30 year = 12×30monts

              =360 months

Now, The monthly payment to the bank is = $1800

Therefore total payments in 360 months is = 360×$1800

                                                                       =$648,000

Bank Interest = $648,000 - $200,000

                      =$448,000

Hence , Heather total interest after 30 years will be =$448,000

To learn more about interest click here:

https://brainly.com/question/27093871

#SPJ2

Step-by-step explanation:

In this question, I see an outlier. Most of the time you may want to solve the inequality, but check how the answers are phrased in relation to the inequality. The equation shows a > symbol.

Answer A states, "save at least $72." If the inequality used a greater than or equal to sign this could work, yet it uses a > symbol. I would go with B & C, if you haven't chosen already.

Answer:

right π/2

Step-by-step explanation:

The function f(x) = 2sin(x - π/2) is a sine function with a period of 2π, an amplitude of 2, and a phase shift of π/2. The phase shift of π/2 causes the graph of the function to be shifted π/2 units to the right. .

Therefore, the correct answer is right π/2

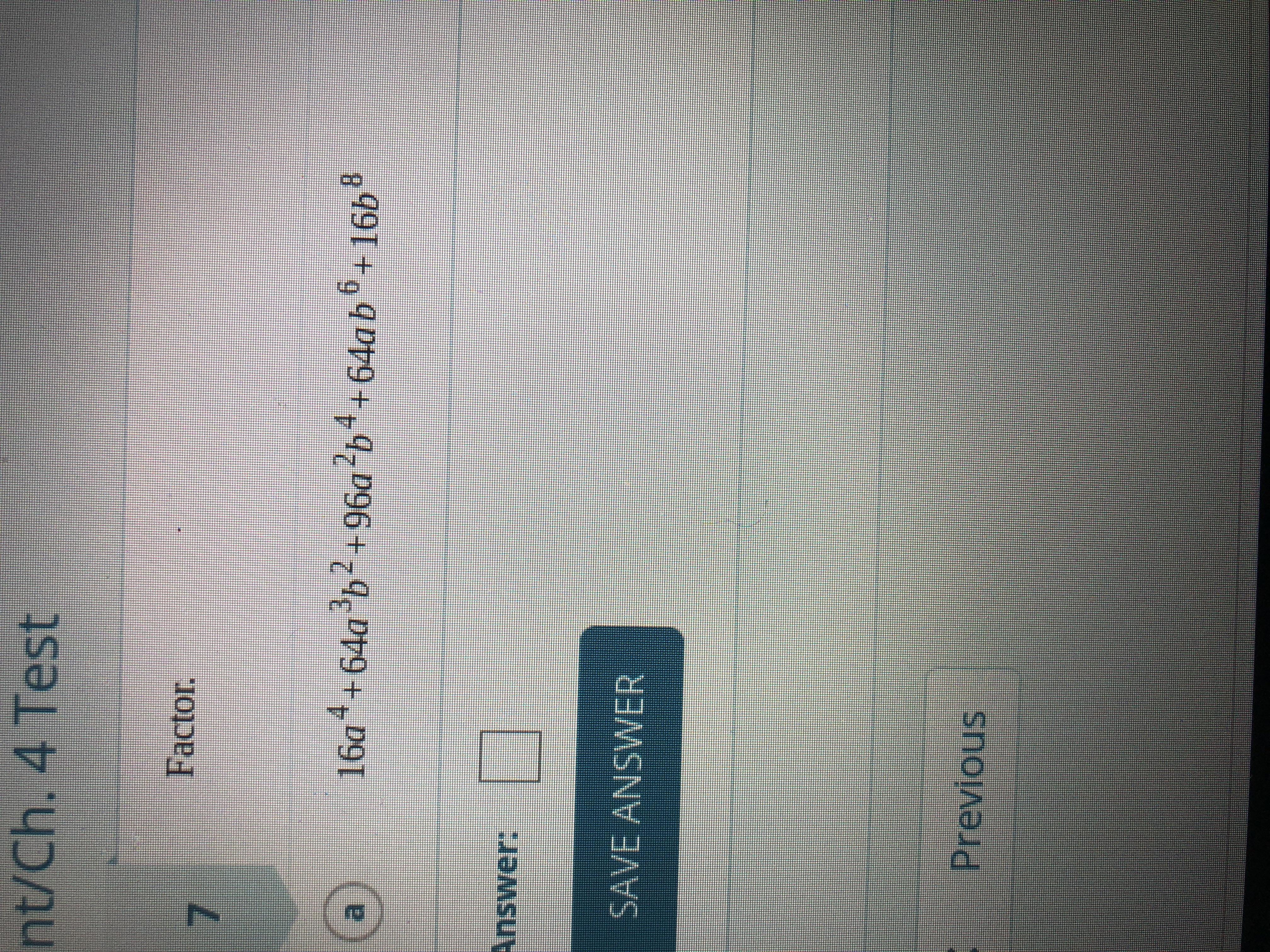
Answer:

Step-by-step explanation:

\(\frac{1}{\sqrt{y} } (\frac{1}{\sqrt{x} -\sqrt{y} } -\frac{1}{\sqrt{x} +\sqrt{y} } )\\=\frac{1}{\sqrt{y} } (\frac{\sqrt{x} +\sqrt{y} -(\sqrt{x} -\sqrt{y} )}{(\sqrt{x} -\sqrt{y} )(\sqrt{x} +\sqrt{y} )} )\\=\frac{1}{\sqrt{y} } (\frac{\sqrt{x} +\sqrt{y} -\sqrt{x} +\sqrt{y} }{(\sqrt{x} )^2-(\sqrt{y} )^2}\\=\frac{1}{\sqrt{y} } (\frac{2\sqrt{y} }{x-y} ) \\=\frac{2}{x-y} ,x\neq y\)

a. It will take 7 months to pay off the credit card.

b. it will take 4 months to pay off the credit card.

Since, APR stands for Annual Percentage Rate. It is the interest rate charged on a loan or credit card, expressed as a yearly percentage rate. The APR takes into account not only the interest rate, but also any fees or charges associated with the loan or credit card.

a. If you put half of the available money each month toward the credit card, then you are paying $150.00 per month towards the credit card balance.

We can use the formula for the present value of an annuity to find how many months it will take to pay off the credit card:

PV = PMT × ((1 - (1 + r)⁻ⁿ) / r)

where:

PV is the present value of the debt

PMT is the payment amount per period

r is the monthly interest rate

n is the number of periods

Substituting the values, we get:

754.43 = 150 × ((1 - (1 + 0.011333)⁻ⁿ) / 0.011333)

Simplifying and solving for n, we get:

n = log(1 + (PV ×r / PMT)) / log(1 + r)

n = log(1 + (754.43×0.011333 / 150)) / log(1 + 0.011333)

n = 6.18

Therefore, it will take 7 months to pay off the credit card if you put half of the available money each month toward the credit card.

b. If you put all of the available money each month toward the credit card, then you are paying $300.00 per month towards the credit card balance.

754.43 = 300 ×((1 - (1 + 0.011333)⁻ⁿ) / 0.011333)

Simplifying and solving for n, we get:

n = log(1 + (PV × r / PMT)) / log(1 + r)

n = log(1 + (754.43× 0.011333 / 300)) / log(1 + 0.011333)

n = 3.43

Therefore, it will take 4 months to pay off the credit card if you put all of the available money each month toward the credit card.

Learn more about APR, visit:

brainly.com/question/13597527

#SPJ1

Answer:

Step-by-step explanation:

3 3 more than x x " can be written as the algebraic expression x+ 3 x +3. But why? Why use math if we can describe things in words? One of the many reasons is that math is more precise and easier to work with than words are. This is a question you should keep thinking about as we dig deeper into algebra.

To know if (-5,5) is a solution to the system, this point should be in the intersection of the two graphs

This means that the point must be in the are where the red and blue colors overlap.

In this case, we can see that (-5,5) is not in the red and blue area

So, (5,-5) is not a solution because the point falls outside of the area with the overlap of shading

In the sketch, the black area is the are where red and blue overlap.

Where they overlap, is the solution. But the point (-5,5) is out of the area. So, Spencer is incorrect.

Correct answer: D.

Answer: The prime factorization of 216 is 2 × 2 × 2 × 3 × 3 × 3 or 23 × 33.

Step-by-step explanation:

PLEASE MARK BRAINLIEST

In order to determine the volume of the sand inside the box, take into account that the shape of the volume of the sand inside the box is the same that the rectangular prism. Then, you can use the folowing formula for the volume of the sand:

V = w·h·l

where w is the width, h the height and l the length. In this case, the height of the sand is 0.25m and the width and the length are the same of the box.

w = 2 m

l = 2.6 m

h = 0.25 m

replace the previous values of the parameters into the formula for V:

V = (2 m)(2.6 m)(0.25 m)

V = 1.3 m³

Hence, the volume of the sand inside the box is 1.3 m³

The distance covered by the sailfish in one second is 0.018 meter.

According to the statement

we have to find that the speed of the sailfish in the per second.

So, For this purpose, we know that the

The given information is:

A sailfish can swim 68.0 mph.

it means it covers a 68 meter distance in the 3600 seconds.

Because we know that the in

1 hour = 3600 sec.

now,

The distance covered in the 1 second = distance covered/ time

Now, substitute the values in it then

The equation become

The distance covered in the 1 second = 68/3600

The distance covered in the 1 second = 0.018 meter.

So, The distance covered by the sailfish in one second is 0.018 meter.

Learn more about distance here

https://brainly.com/question/17273444

#SPJ9

The two points of tangency are (-1,3) and (1,-3).

What is the equation of a tangent to the circle?

The equation of a tangent to a circle is a linear equation that describes a line that touches the circle at exactly one point, without crossing it. A tangent line is perpendicular to the radius of the circle at the point of contact.

Since the line T is tangent to the circle, the radius of the circle drawn to the point of tangency (-1,3) is perpendicular to the line T. Therefore, the center of the circle must lie on the line perpendicular to T at (-1,3).

The equation of the tangent line T can be found by taking the derivative of the equation of the circle and evaluating it at the point of tangency (-1,3):

2x + 2y(dy/dx) = 0

dy/dx = -x/y

At the point (-1,3), dy/dx = -(-1)/3 = 1/3. Therefore, the equation of the tangent line T is:

y - 3 = (1/3)(x + 1)

y = (1/3)x + 10/3

The slope of any line perpendicular to T is -3 (the negative reciprocal of 1/3). The point-slope form of the equation of a line with slope -3 passing through (-1,3) is:

y - 3 = -3(x + 1)

y = -3x

To find the points of tangency, we need to solve the system of equations consisting of the equation of the circle and the equation of the tangent line:

x² + y² = 10

y = -3x

Substituting y = -3x into the first equation, we get:

x² + (9x²) = 10

10x² = 10

x² = 1

x = ±1

Substituting these values of x into y = -3x, we get:

(-1,3) and (1,-3)

Therefore, the two points of tangency are (-1,3) and (1,-3).

To learn more about the equation of the tangent to the circle, visit:

https://brainly.com/question/30760562

#SPJ1

Answer:

Hey mate....

Step-by-step explanation:

This is ur answer....

5/3 = x/6

= 5×6/3 = x

= 30/3 = x

= 10 = x

= x = 10

Hope it helps!

Brainliest pls!

Follow me! ♧

Answer:

x=10

Step-by-step explanation:

3*2=6 and using giant one its 5*2 which is 10

10/6

The angle sum property of a triangle and the angle formed between a tangent and a radius of a circle indicates.

m∠ADC = 58°

A tangent to a circle is a straight line which touches the circumference of a circle at only one point.

The vertical angles theorem indicates that we get;

∠1 ≅ ∠2

Therefore; m∠1 = m∠2

The tangent to a circle indicates that we get;

The angle formed at vertex B and Q are 90 degrees angles and the triangles ABP and AQP are right triangles, which indicates that the acute angles of each of the right triangles are complementary, therefore;

m∠1 + 26° = 90°

m∠1 = 90° - 26° = 64°

Therefore, m∠2 = m∠1 = 64°

m∠2 = m∠CAD = 64°

The segments AC and AD are radial lengths therefore, the triangle ΔACD is an isosceles triangle.

m∠ADC ≅ m∠ACD (Base angles of an isosceles triangle)

The angles ∠ADC and ∠ACD are therefore;

m∠CAD + m∠ADC + m∠ACD = 180° (Angle sum property of a triangle)

m∠CAD + m∠ADC + m∠ADC = 180°

m∠CAD + 2 × m∠ADC = 180°

64° + 2 × m∠ADC = 180°

m∠ADC = (180° - 64°)/2 = 58°

m∠ADC = 58°

Learn more on the angle sum property of a triangle here: https://brainly.com/question/22262639

#SPJ1

The two pairs of integers that satisfy the given conditions are (-3, 8) and (5, 24).

To solve the system of equations, let's assign variables to the two integers. Let the first integer be represented by 'x' and the second integer by 'y'.

According to the given information:

a. Fourteen more than twice the first integer gives the second integer:

This can be expressed as: 2x + 14 = y

b. The second integer increased by one is the square of the first integer:

This can be expressed as: y + 1 = x^2

Now, we have a system of equations:

1) 2x + 14 = y

2) y + 1 = x^2

To solve this system, we can substitute the value of 'y' from equation 1) into equation 2):

2x + 14 + 1 = x^2

2x + 15 = x^2

Rearranging the equation, we have:

\(x^2 - 2x - 15 = 0\)

Factoring the quadratic equation, we get:

(x - 5)(x + 3) = 0

Setting each factor equal to zero:

x - 5 = 0   -->   x = 5

x + 3 = 0   -->   x = -3

Substituting the values of 'x' back into equation 1), we can find the corresponding values of 'y':

For x = 5:

2(5) + 14 = y

10 + 14 = y

y = 24

For x = -3:

2(-3) + 14 = y

-6 + 14 = y

y = 8

Therefore, the two pairs of integers that satisfy the given conditions are (-3, 8) and (5, 24).

for more such question on integers visit

https://brainly.com/question/929808

#SPJ8

P Q P V Q P ^ Q P -> Q -P -Q -P V -Q -P -> Q -P -> -Q P <-> Q

T T T T T F F F F F T    T

F T T F F T T T T T F    F

P F T F F T T T T T F     F

-P T T F F T T T T T F     F

-Q T T T T F T F F F T     T

-P V -Q T T F F T T T T T F

-P -> Q T T F F T T T T T F

-P -> -Q T T F F T T T T T F

P <-> Q T T T T F T T T T F

Here is a more detailed explanation of how I filled out the table:

P | Q : This column is simply the truth value of P and Q. If P and Q are both true, then the entry in this column is T. If P is true and Q is false, then the entry in this column is F. If P is false and Q is true, then the entry in this column is F. And if P and Q are both false, then the entry in this column is T.

P V Q : This column is the truth value of P or Q. If P is true, then the entry in this column is T. If Q is true, then the entry in this column is T. And if P and Q are both false, then the entry in this column is F.

P ^ Q : This column is the truth value of P and Q. If P and Q are both true, then the entry in this column is T. And if P and Q are both false, then the entry in this column is F.

P -> Q : This column is the truth value of P implies Q. If P is true and Q is false, then the entry in this column is F. And if P is false or Q is true, then the entry in this column is T.

-P : This column is the negation of P. If P is true, then the entry in this column is F. And if P is false, then the entry in this column is T.

-Q : This column is the negation of Q. If Q is true, then the entry in this column is F. And if Q is false, then the entry in this column is T.

-P V -Q : This column is the truth value of not P or not Q. If P and Q are both true, then the entry in this column is F. If P and Q are both false, then the entry in this column is T. And if P or Q is true, then the entry in this column is T.

-P -> Q : This column is the truth value of not P implies Q. If P is true and Q is false, then the entry in this column is T. And if P is false or Q is true, then the entry in this column is F.

-P -> -Q : This column is the truth value of not P implies not Q. If P and Q are both true, then the entry in this column is T. If P is false or Q is false, then the entry in this column is T. And if P is true and Q is true, then the entry in this column is F.

P <-> Q : This column is the truth value of P if and only if Q. If P and Q are both true or P and Q are both false, then the entry in this column is T. And if P and Q have different truth values, then the entry in this column is F.

for more such questions on truth value

https://brainly.com/question/7483637

#SPJ8

Answer:

the answer is 2

Step-by-step explanation:

Answer:

Step-by-step explanation:

It is 2, because it is the only factor that can go with both of the numbers.

The pair that support Angle-Side-Angle Postulate (ASA) be used to prove that △ABC≅△XYZ is option B

Triangles are said to be congruent when the sides and angles equal in accordance to to the triangle congruency rules

examples of these rules are

The problem requires the prove by Angle - Side- Angle = ASA to ensure that the the triangles are congruent

The Angle - Side - Angle = ASA have it that the two triangles being compared should have their two angles and the included side being equal

Learn more about congruent triangles here:

https://brainly.com/question/29393764
#SPJ1

For the equations 2xy - y^2 = 1 and xy + x + y = x^2y^2 using implicit differentiation the value Dxy is given by Dxy = (1 - 2xy + 3y^2)/(x - y)^3 and Dxy = (2y^2 - 2xy - 3y - 1)/(x - 2xy + 1)^3  respectively.

Equation 2xy - y^2 = 1,

Differentiate both sides of the equation with respect to x,

Treating y as function of x and then differentiate again with respect to x.

Using implicit differentiation,

First, differentiate both sides with respect to x,

2y + 2xy' - 2yy' = 0

Next, solve for y',

⇒2xy' - 2yy' = -2y

⇒y' (2x - 2y) = -2y

⇒y' = -y/(x - y)

Now, differentiate again with respect to x,

y''(x - y) - y'(2x - 2y) = y/(x - y)^2

Substitute the expression we obtained for y' in terms of y and x,

y''(x - y) - (-y/(x - y))(2x - 2y) = y/(x - y)^2

Simplify and solve for y'',

y''(x - y) + (2xy - 3y^2)/(x - y)^2 = 1/(x - y)^2

The expression for Dxy is,

Dxy = (1 - 2xy + 3y^2)/(x - y)^3

For the equation xy + x + y = x^2y^2,

Differentiate both sides of the equation with respect to x,

Using implicit differentiation,

First, differentiate both sides with respect to x,

⇒y + xy' + 1 + y' = 2xyy'

Solve for y',

⇒xy' - 2xyy' + y' = -y - 1

⇒y' (x - 2xy + 1) = -y - 1

⇒y' = -(y + 1)/(x - 2xy + 1)

Now, differentiate again with respect to x,

y''(x - 2xy + 1) - y'(2y - 2x y' + 1) = (y + 1)/(x - 2xy + 1)^2

Substitute the expression we obtained for y' in terms of y and x,

y''(x - 2xy + 1) - (-y - 1)/(x - 2xy + 1)^2 (2y - 2x y' + 1) = (y + 1)/(x - 2xy + 1)^2

Simplify and solve for y''

y''(x - 2xy + 1) - (2y^2 - 2xy - 2y)/(x - 2xy + 1)^2 = (y + 1)/(x - 2xy + 1)^2

The expression for Dxy is,

Dxy = (2y^2 - 2xy - 3y - 1)/(x - 2xy + 1)^3

Therefore , the value of Dxy using implicit differentiation for two different functions is equal to

Dxy = (1 - 2xy + 3y^2)/(x - y)^3 and Dxy = (2y^2 - 2xy - 3y - 1)/(x - 2xy + 1)^3

Learn more about implicit differentiation  here

brainly.com/question/20709669

#SPJ4

Answer: 123.05

Use annuity formula

Answer:

Step-by-step explanation:

Since we're talking about making a deposit of a certain amount every month rather than just one big deposit, we are talking about an annuity. The formula for the value of an annuity is A(t)=d[(1+rn)nt−1](rn) where A(t) is the value of the annuity, d is the amount of each deposit, n is the number of deposits per year, t is the number of years, and r is the rate of interest. In this case we know we want the value of the annuity to be A(t)=$150,000, we want to make deposits every month, or 12 times a year, so n=12, we want to reach our desired value in 30 years, so t=30, and our account earns 7% interest, so r=0.07. We can plug in all of these values and solve for d to find the amount we need to deposit each month:

A(t)150,000150,000150,000d=d[(1+rn)nt−1](rn)=d[(1+0.0712)12⋅30−1]0.0712≈d[(1.00583)360−1]0.00583≈1,219.97d≈122.95

The amount you need to deposit each month is approximately $122.95.