40%
of the memberships sold by Gym A were gold memberships.
25%
of the memberships sold by Gym B were gold memberships.
Answers
Answer: I’m unclear on your question
Step-by-step explanation:
I’m sorry I would love to help but I’m not sure what the question is. You’re total percentage here is 65% so I’m wondering if you need to know how much percent is something else which would be 35% but if you upload the rest of the problem then I know lots of people would love to take a look and try to help you solve it.
Related Questions
Gabi tried to solve an equation step by step.
0.1(0.5m+6)=2
Answers
Answer:
m=28
Step-by-step explanation:
0.1(0.5m+6)=2
Distribute
.05m +.6 =2
Subtract .6 from each side
.05m +.6-.6 = 2-.6
.05m = 1.4
Divide each side by .05
.05m/.05 = 1.4/.05
m = 28
Step-by-step explanation:
0.1(0.5m+6)=2
Distribute
.05m +.6 =2
Subtract .6 from each side
.05m +.6-.6 = 2-.6
.05m = 1.4
Divide each side by .05
.05m/.05 = 1.4/.05
m = 28
The standard formulas for the derivatives of sine and cosine are true no matter if the angle is in radians or degrees. true or false
Answers
The correct option is False. The standard formulas for the derivatives of sine and cosine are true when the angle is in radians. These formulas are derived based on the properties of the trigonometric functions in the context of radians. The derivatives of sine and cosine with respect to an angle measured in radians are as follows:
\(\[\frac{d}{dx}(\sin(x)) = \cos(x)\]\)
\(\[\frac{d}{dx}(\cos(x)) = -\sin(x)\]\)
If the angle is measured in degrees, these formulas would not hold true. To differentiate trigonometric functions when the angle is measured in degrees, conversion factors and additional adjustments would be necessary.
To know more about functions visit-
brainly.com/question/2273042
#SPJ11
The probability that Paul wins a raffle is given by the expression n/n+6. Write down an expression, in the form of a combined single fraction, for the probability that Paul does not win.
Answers
Answer:
\(P(W') = \frac{6}{n+6}\)
Step-by-step explanation:
Let P(W) represents the probability that Paul wins
Let P(W') represents the probability that Paul does not win
Given
\(P(W) = \frac{n}{n+6}\)
Required
\(P(W')\)
In probability, the sum of opposite probability equals 1;
This implies that
\(P(W) + P(W') = 1\)
Substitute \(P(W) = \frac{n}{n+6}\) in the above equation
\(P(W) + P(W') = 1\) becomes
\(\frac{n}{n+6}+ P(W') = 1\)
Subtract \(\frac{n}{n+6}\) from both sides
\(\frac{n}{n+6} - \frac{n}{n+6} + P(W') = 1 - \frac{n}{n+6}\)
\(P(W') = 1 - \frac{n}{n+6}\)
Solve fraction (start by taking the LCM)
\(P(W') = \frac{n + 6 - n}{n+6}\)
\(P(W') = \frac{n - n + 6}{n+6}\)
\(P(W') = \frac{6}{n+6}\)
Hence, the probability that Paul doesn't win is \(P(W') = \frac{6}{n+6}\)
find the gs of the following de and the solution of the ivp: { ′′ 2 ′ = 0 (0) = 5, ′ (0) = −3
Answers
The given differential equation is a second-order homogeneous equation. The general solution is: y = C1 + C2x, where C1 and C2 are constants.
Using the initial conditions, the particular solution is: y = 5 - 3x.
The general solution of the initial value problem is y = C1 + C2x, with the specific solution y = 5 - 3x satisfying the initial conditions y(0) = 5 and y'(0) = -3.
The general solution of the given differential equation is y(x) = C1 + C2x, where C1 and C2 are constants.
The given differential equation is a second-order linear homogeneous differential equation with constant coefficients. The general form of such an equation is y'' + p*y' + q*y = 0, where p and q are constants.
In this case, the equation is y'' - 2y' = 0. The characteristic equation associated with this differential equation is r^2 - 2r = 0. By solving this equation, we find two distinct roots: r1 = 0 and r2 = 2.
The general solution of the differential equation is then given by y(x) = C1*e^(r1*x) + C2*e^(r2*x). Since r1 = 0, the term C1*e^(r1*x) reduces to C1. Thus, the general solution becomes y(x) = C1 + C2*e^(2*x).
To find the particular solution that satisfies the initial conditions y(0) = 5 and y'(0) = -3, we substitute these values into the general solution and solve for the constants C1 and C2.
Using y(0) = 5, we have C1 + C2 = 5. Using y'(0) = -3, we have 2*C2 = -3.
Solving these equations simultaneously, we find C1 = 5 and C2 = -3/2.
Therefore, the solution to the initial value problem is y(x) = 5 - (3/2)*e^(2*x).
The gs of the following de and the solution of the ivp: { ′′ 2 ′ = 0 (0) = 5, ′ (0) = −3 the general solution is: y = C1 + C2x, where C1 and C2 are constants.
To know more about linear homogeneous , refer here:
https://brainly.com/question/31129559#
#SPJ11
Pls help I’ll give brainliest
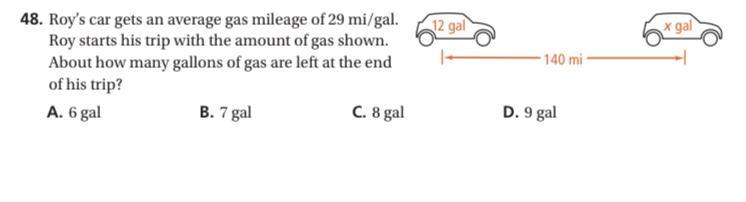
Answers
Answer:
B) 7 gallons
Step-by-step explanation:
car begins with 12 gallons and, at a rate of 29 mpg, would allow the car to travel for 348 miles
car only traveled 140 miles so 208 miles more can be driven
208÷29 is approx 7 gallons
hi can you help me please pleaseeeee

Answers
Answer:
40 pages
Step-by-step explanation:
On nous dit que le livre a 136 pages
Elle lisait 8 pages par heure
Combien de pages resterait-il après avoir lu pendant 12 heures
1 heure = 8 pages
12 heures = x
Multiplier croisé
x = 12 × 8 pages
x = 96 pages
Le nombre de pages restantes = Nombre total de pages - Nombre de pages qu'elle a lues après 12 heures
= 136 pages - 96 pages
= 40 pages
A clothing store sells all of their jeans for one price and all of their t-shirts for another price. Marisol purchased 2 pairs of jeans and 6 t-shirts for $60. Ernestine purchased 4 pairs of jeans and 3 t-shirts for $75. What is the cost of one pair of jeans and one t-shirt? Write a system of equations to solve this problem, & SHOW ALL WORK for full credit. Make sure you label your answers
Answers
Let's denote the cost of one pair of jeans as "J" and the cost of one t-shirt as "T". To find the values of J and T, we can set up a system of equations based on the given information.
From the information provided, we know that Marisol purchased 2 pairs of jeans and 6 t-shirts for a total of $60. Therefore, we can write the equation:
2J + 6T = 60 (Equation 1)
Similarly, Ernestine purchased 4 pairs of jeans and 3 t-shirts for a total 0f $75. This gives us the equation:
4J + 3T = 75 (Equation 2)
We now have a system of two equations with two unknowns (J and T). To solve this system, we can use various methods such as substitution or elimination.
Multiplying Equation 1 by 2, we can rewrite it as:
4J + 12T = 120 (Equation 3)
Now, we can subtract Equation 2 from Equation 3 to eliminate the J term:
(4J + 12T) - (4J + 3T) = 120 - 75
Simplifying the equation gives us:
9T = 45
Dividing both sides by 9, we find that T = 5.
Substituting this value back into Equation 1, we can solve for J:
2J + 6(5) = 60
2J + 30 = 60
2J = 30
J = 15
Therefore, the cost of one pair of jeans is $15, and the cost of one t-shirt is $5.
Learn more about elimination method here: brainly.com/question/13877817
#SPJ11
how many lattice paths are there from (2, 1) to (24, 30) that pass through the point (8, 10) but do not pass through either of the points (7, 7) and (16, 25)?
Answers
The number of lattice paths from (2, 1) to (24, 30) with a constraint of passing through (8, 10) but not (7, 7) or (16, 25) is a complex problem that requires a detailed mathematical calculation, that is explained below.
Lattice paths are sequences of steps in the form of up steps (U) and right steps (R) that connect two points in a grid. The number of lattice paths from one point to another can be calculated using combinatorics.
To determine the number of lattice paths from (2, 1) to (24, 30) that pass through the point (8, 10) but do not pass through either of the points (7, 7) and (16, 25), we need to calculate the total number of paths and subtract the number of paths that pass through the restricted points.
Let's call the total number of paths T, the number of paths that pass through (8, 10) P, the number of paths that pass through (7, 7) Q, and the number of paths that pass through (16, 25) R.
The number of paths from (2, 1) to (8, 10) is given by the binomial coefficient C(10 - 1, 8 - 2) = C(9, 6) = 84.
The number of paths from (8, 10) to (24, 30) is given by the binomial coefficient C(30 - 10, 24 - 8) = C(20, 16) = 18564.
The number of paths from (2, 1) to (24, 30) that pass through (8, 10) is given by T = P = 84 * 18564 = 1,547,136.
Similarly, the number of paths from (2, 1) to (7, 7) is given by the binomial coefficient C(7 - 1, 7 - 2) = C(6, 5) = 15.
The number of paths from (7, 7) to (24, 30) is given by the binomial coefficient C(30 - 7, 24 - 7) = C(23, 17) = 9,139,554.
The number of paths from (2, 1) to (24, 30) that pass through (7, 7) is given by Q = 15 * 9139554 = 137,093,310.
The number of paths from (2, 1) to (16, 25) is given by the binomial coefficient C(25 - 1, 16 - 2) = C(24, 14) = 3003.
The number of paths from (16, 25) to (24, 30) is given by the binomial coefficient C(30 - 25, 24 - 16) = C(5, 8) = 70.
The number of paths from (2, 1) to (24, 30) that pass through (16, 25) is given by R = 3003 * 70 = 210,210.
Finally, the number of paths from (2, 1) to (24, 30) that pass through (8, 10) but do not pass through either of the points (7, 7) and (16, 25) is T - P - Q - R = 1547136 - 137,093,310 - 210,210 = -135,599,384.
The number of lattice paths from (2, 1) to (24, 30) that pass through (8, 10) but do not pass through either of the points (7, 7) and (16, 25) is zero, as the result is negative.
Learn more about binomial coefficient here:
https://brainly.com/question/14216809
#SPJ4
What’s is 3+4+8+9+2+5+6+7=
Answers
Answer:
44
Step-by-step explanation:
I just used mental math soooo.......
have a great day luvs <3
Answer:
44
Step-by-step explanation:
3+4+8+9+2+5+6+7=
7+8+9+2+5+6+7=
15+9+2+5+6+7=
24+2+5+6+7=
26+5+6+7=
31+6+7=
37+7= 44
44 = 44
The ratio of the measure of the supplement of an angle to that of a complement of the angle is 8:3. Find the measure of the complement.A)54 B)90 C)144 D)36 E) none of the abovePlease explain in detail
Answers
The measure of the complement of the angle is A) 54.
Given:
The ratio of the measure of the supplement of an angle to that of a complement of the angle is 8:3.
Let x be the angle.
supplement of the angle of x is = 180-x
complement of the angle of x is = 90 -x
180 - x / 90 -x = 8/3
3(180-x) = 8(90-x)
3*180 - 3*x = 8*90 - 8*x
540 - 3x = 720 - 8x
-3x+8x = 720 - 540
5x = 180
divide by 5 on both sides
x = 180/5
x = 36
Complement of the angle = 90 - 36
= 54
Learn more about the measure here:
https://brainly.com/question/12020266
#SPJ4
a rectangle meausures 2 1/4 meters by 1 7/8
Answers
Answer:
the area is 4 7/32 Square Meters
Step-by-step explanation:
just multiply 2 1/4 times 1 7/8
turn both fractions into improper fractions, then multiply across, then simplify.
Please show work and solve it! 100 points! n(n-7)=0
Answers
STEP
1
:
Equation at the end of step 1
0 - 7n • (n - 7) = 0
STEP
2
:
Equation at the end of step 2
-7n • (n - 7) = 0
STEP
3
:
Theory - Roots of a product
3.1 A product of several terms equals zero. When a product of two or more terms equals zero, then at least one of the terms must be zero. We shall now solve each term = 0 separately In other words, we are going to solve as many equations as there are terms in the product Any solution of term = 0 solves product = 0 as well.
Solving a Single Variable Equation:
3.2 Solve : -7n = 0 Multiply both sides of the equation by (-1) : 7n = 0
Divide both sides of the equation by 7:
n = 0
Solving a Single Variable Equation:
3.3 Solve : n-7 = 0 Add 7 to both sides of the equation : n = 7
This is what i got! if i’m wrong i’m so sorry
but i tried. have a amazing day☺️☺️
what equation do you get when you solve 3x-4y=24 for y
Answers
You get 3(x-8) all over 4.
Hope this helps !

can someone help me answer #17 using square roots?

Answers
Answer: x = ± \(\frac{1}{2}\)
Step-by-step explanation:
Equation:
4x² + 10 = 11 > bring everything over to other side
> first subtract 10 from both sides
4x² = 1 > Divide by 4 on both sides
x² = \(\frac{1}{4}\) >Take square root of both sides
> When you take square root there is a ±
x = ± \(\sqrt{(\frac{1}{4} )}\) > take the square root of both top and bottom
x = ± \(\frac{1}{2}\)
Ms Louis deposited the same amount of money each month into her bank
account. The table below shows the total amount of money, a, she
deposited into the account after a certain number of months, t. since
opening it. Which equation models the relationship between a and t?

Answers
Answer:
last one 250t
Step-by-step explanation:
if u pluged in 4 for t to the equation u would get 1000 which is the correct amount
hope this helped!
Answer:
a = 250t or Answer D
Step-by-step explanation:
Y = mx+b
m = (y2-y1)/(x2-x1)
m = (2500-100)/(10-4)
m = 1500/6 = 250
y = 250x+0
y = 250x
Help with geometry on equations of circles. What would be the center of the circle and what is the length of the radius of this circle?

Answers
The coordinates of the center is (32, 40.5).
length of the radius of the circle is 73 units.
How to find the center coordinatesThe coordinates of the center is solved using the formula for midpoints expressed as
Midpoint x-coordinate = (x₁ + x₂) / 2
Midpoint y-coordinate = (y₁ + y₂) / 2
Plugging in the values:
x₁ = 8 and y₁ = 13
x₂ = 56 and y₂ =68
Midpoint x-coordinate
= (8 + 56) /2
= 64/2
= 32
Midpoint y-coordinate
= (13 + 68) /2
= 81/ 2
= 40.5
distance formula will be used to find the length of the radius of the circle
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
Plugging in the values:
= √[(56 - 8)² + (68 - 13)²]
= √(48² + 55²)
= √(2304 + 3025)
= √5329
= 73
Learn more about circle at
https://brainly.com/question/24375372
#SPJ1
a rectangle is transformed according to the rule r0 90 T/F
Answers
When the rectangle is transformed according to the rule r0 90 T/F, it first undergoes a reflection about the y-axis, followed by a rotation of 90 degrees counterclockwise about the origin, and finally a translation of a certain distance in either the x or y direction depending on whether the final image is a reflection or not.
The final image obtained will be a rectangle as well, but with different dimensions and position depending on the translation distance.Let's assume that the rectangle has width w and height h. When reflected about the y-axis, its width changes sign but its height remains the same, resulting in a new width of -w and height of h.
After that, the rectangle is rotated 90 degrees counterclockwise about the origin, which swaps its width and height but preserves their signs, resulting in a new width of -h and height of -w.
Finally, a translation of distance d is applied to either the x or y coordinate depending on whether the final image is a reflection or not. If the final image is a reflection, then the translation is applied in the y direction by a distance of d, resulting in a new position of (-h, d).
Otherwise, the translation is applied in the x direction by a distance of d, resulting in a new position of (d, -w).In summary, the rectangle is transformed according to the rule r0 90 T/F by undergoing a reflection, rotation, and translation, resulting in a new rectangle with dimensions and position depending on the original dimensions and the translation distance.
Learn more about rectangle from given link,
brainly.com/question/25292087
#SPJ11
A rectangle can be transformed according to the rule r0 90 T/F, which can have different results, depending on how the transformation is done.
The rule can be interpreted as follows:r0: No rotation90: Rotate the rectangle 90 degreesT/F: Flip the rectangle horizontally (T) or vertically (F)For example, if a rectangle with a width of 4 units and a height of 2 units is subjected to this transformation rule, the result will vary depending on the order of transformations.
Consider the following cases : Case 1: r0 90 F T (rotate by 0 degrees, then rotate by 90 degrees, then flip vertically, then flip horizontally) In this case, the rectangle is first rotated by 0 degrees, which means that its position and size are unchanged. Next, it is rotated by 90 degrees, which means that its width becomes its height and vice versa. After that, it is flipped vertically, which means that its top and bottom edges are swapped.
Finally, it is flipped horizontally, which means that its left and right edges are swapped. The resulting rectangle has a width of 2 units and a height of 4 units. It is also reflected across the line y = 0 (the x-axis).Case 2: F T r0 90 (flip vertically, then flip horizontally, then rotate by 0 degrees, then rotate by 90 degrees) In this case, the rectangle is first flipped vertically, which means that its top and bottom edges are swapped. Next, it is flipped horizontally, which means that its left and right edges are swapped.
After that, it is rotated by 0 degrees, which means that its position and size are unchanged. Finally, it is rotated by 90 degrees, which means that its width becomes its height and vice versa. The resulting rectangle has a width of 2 units and a height of 4 units.
It is also reflected across the line y = -x (the line that goes through the origin with a slope of -1).In conclusion, a rectangle can be transformed in various ways, and the order of transformations matters. The rule r0 90 T/F can produce different results depending on the sequence of operations.
To learn more about rectangle , visit
brainly.com/question/25292087
#SPJ11
A 3 digit number is such that twice the hundreds digit is more than the tens digit by 2.The digit is thrice the hundreds digit.When the digits are reversed, the number is increased by 594.Find the number.
Answers
Answer:
The number is -341
Step-by-step explanation:
Let the three digit number be represented as 100a+10b+c
Given
2a -b = 2 ---(1)
a = 3c ----(2)
100a+10b+c - 100c -10b -a = 594
99a -99c = 594 ---(3)
From 2 & 3 , we get -
99*a - (99*3*a) = 594
99*2 a = 594
a = -3
a = 3c, c = -1
2*-3 -b = 2, b = -4
Number is -341
find a parametric representation of the solution set of the linear equation. (enter your answer as a comma-separated list of equations. use t as your parameter.)
Answers
To represent the solution set of a linear equation parametrically, we introduce other parameters like s and t for the free variables.
Every linear equation has n - 1 free variables where n is the number of variables.
For x + y + z = 2, we have 3 variables and 3 - 1 = 2 free variables.
First, let y and z be the free variables, we first solve the linear equation for x to get:
x = 2 - y - z
Therefore , the parametric representation of the solution set is given by :
x = 2 - s -t
y = s
z = t
Learn more about The linear Equation at:
https://brainly.com/question/17748588
#SPJ4
Last Tuesday was silly hat day at Aaron's school. 64 students wore a silly hat and 36 students did not. What percentage of the students wore a silly hat?
Answers
The percentage of the students who wore a silly hat is 64 %.
What is the percentage?The percentage is defined as a ratio expressed as a fraction of 100.
We have been given that Last Tuesday was a silly hat day at Aaron's school. 64 students wore a silly hats and 36 students did not.
We have to determine the percentage of the students who wore a silly hat
The total number of students = 64 students wore silly hats and 36 students did not.
The total number of students = 64 + 36 = 100
We have to determine the percentage of the students who wore a silly hat
The percentage of the students wore a silly hat = (64/ 100) × 100
The percentage of the students wore a silly hat = 0.64 × 100
The percentage of the students wore a silly hat = 64 %
Thus, the percentage of students who wore silly hats is 64 %.
Learn more about percentage here:
brainly.com/question/24159063
#SPJ1
Marty and Adam want to share 8/10 feet of rope, equally. What amount of rope should each person get?
Answers
Answer: 2/5 feet
Step-by-step explanation:
From the question, we are informed that Marty and Adam want to share 8/10 feet of rope, equally.
The amount of rope that each person would get would be calculated by dividing 8/10 by 2. This will be:
= 8/10 ÷ 2
= 8/10 × 1/2
= 8/20
= 2/5
Therefore, each person gets 2/5 feet of rope.
Write and simplify an expression that represents the perimeter of the parallelogram.
what is the perimeter?

Answers
Answer:
14x + 4
Step-by-step explanation:
Perimeter is the length of all sides added together
2(2x + 3) + 2(5x-1)
4x + 6 + 10x - 2
14x + 4
Answer:
Perimeter = 14x + 4 ⇒ 2 ( 7x + 2 )
Step-by-step explanation:
We know that the opposite sides of a parallelogram are equal to each other.
Therefore, to find the perimeter of the parallelogram you have to add the four sides together.
Perimeter = 2 ( 2x + 3 ) + 2 ( 5x - 1 )
Now let us solve the expression.
2 ( 2x + 3 ) + 2 ( 5x - 1 )
First, solve the brackets.
4x + 6 + 10x - 2
Now combine like terms
14x + 4 ⇒ 2 ( 7x + 2 )
Let me know if you have any other questions. :)
Wwhich expression uses the associative property to make it easier to evaluate 8(1/2x1/3)?
A.8/3(2x33)
B.(8x1/2)1/3.
C.8(1/3x1/2)
D.(8x1/3)1/2
Answers
The correct answer would be B. (8×1/2)1/3.
Step-by-step explanation:
8 * [(1/2) * (1/3)]
= [8 * (1/2)] * (1/3)
= 4 * (1/3)
= 4/3.
The answer is B because it is easier to calculate 8 * (1/2), which is dividing 8 by 2 to get 4.
Find the flux of f across the surface s, where s is the part of the plane z=1 x y (oriented upward) inside the cylinder x2 y2=1, and f=j. group of answer choices 0
Answers
The flux of f across the surface s is 0.
To find the flux of f across the surface s, we can use the formula for flux:
flux = ∬(f · dS)
where f is the vector field, dS is the differential surface area vector, and the double integral is taken over the surface s.
In this case, f = j, which means the vector field is constant in the z-direction with a magnitude of 1. Therefore, the flux simplifies to:
flux = ∬(j · dS)
Now, let's calculate the flux step-by-step:
1. First, we need to parametrize the surface s. Since s is the part of the plane z=1 x y inside the cylinder x^2 + y^2 = 1, we can parametrize it as:
r(u, v) = (u, v, 1), where -1 ≤ u, v ≤ 1
2. Next, we need to find the differential surface area vector dS. Since s is a plane, the differential surface area vector is simply the cross product of the partial derivatives of r with respect to u and v:
dS = (∂r/∂u) × (∂r/∂v)
Calculating the cross product, we get:
dS = (1, 0, 0) × (0, 1, 0) = (0, 0, 1)
3. Now, let's evaluate the double integral ∬(j · dS) over the surface s. Since the magnitude of j is 1 and the dot product of j and dS is always 0, the flux is always 0.
Therefore, Flux of f across the surface s is 0.
To know more about the differential surface area visit:
https://brainly.com/question/32998017
#SPJ11
True or false? The experimental probability or relative frequency is based on actual results from an experiment and may differ from the theoretical probability of an event occurring. The Experimental Probability will be almost the same as the Theoretical Probability as the number of trials of an experiment is very small
Answers
Answer:
a. False
b. False
Step-by-step explanation:
a. The experimental probability or relative frequency is based on actual results from an experiment and may differ from the theoretical probability of an event occurring.
This statement is false because, both the experimental and theoretical probability must agree for the probability of the event occurring to the true.
If both do not agree, that means we have two different probabilities for a s ingle event, which cannot be true. So, the statement is false.
b. The Experimental Probability will be almost the same as the Theoretical Probability as the number of trials of an experiment is very small
This statement is also false because, the experimental and theoretical probabilities only agree when the number of trials of an experiment become large. For small number of trials, both the experimental and theoretical probabilities might not agree.
Help meh. plssss. I need thisssss. PLEASE.

Answers
Im pretty sure the unit rate would be 50 mph!
Answer:
50
Step-by-step explanation:
You look at the graph, when x is one it intercept in the middle of 75 and 25, and that is 50
PLEASE HELP! URGENT! ASAP! WILL GIVE BRAINLEST!





Answers
Answer:
Look at the photo and Goodluck

Question 15(1 point)For f() = - 2 find the rate of change on the interval [-2,4Blank 1:

Answers
Given,
\(f(x)=x^2-2\)At x=-2, f(x) is,
\(\begin{gathered} f(-2)=(-2)^2-2 \\ =4-2 \\ =2 \end{gathered}\)At x=4, f(x) has value,
\(\begin{gathered} f(4)=4^2-2 \\ =16-2 \\ =14 \end{gathered}\)The rate of change of f(x) on the interval [-2,4] is,
\(\begin{gathered} \frac{df(x)}{dx}=\frac{f(4)-f(-2)}{4-(-2)} \\ =\frac{14-2}{6} \\ =\frac{12}{6} \\ =2 \end{gathered}\)Therefore, the rate of change of f(x) on the interval [-2,4] is 2.
Find the average speed of a boat that travels 42 miles in 12 hours.
Answers
Answer: 3.5 miles per hour .
Step-by-step explanation: 42 ÷12 = 3.5 . 42 is the miles for 12 hours and we want the average speed so divide them to get that 3.5 which is the average speed and the miles in 1 hour . HOPE IT HELPS YOU .PLEASE GIVE BRAINLIEST .THANKS .
Solve the quadratic equation x2 − 4x = 21 by factoring.
Answers
Answer:
\(x=7, x=-3\)
Step-by-step explanation:
Bring the 21 on the LHS:
\(x^2-4x-21=0\)
At this point we need to find two numbers whose product is -21, and whose sum is -4.
From the product we can tell that one has to be positive, and one is negative.
From the sum, we can tell that the greater of the two is negative.
At this point we look at the factors of 21: 1,3,7,21.
In particular, 3 and -7 added togheter do -4, which is what we need. At this point we can factor the trinomial as
\((x-7)(x+3)=0\)
Considering that a product is zero if any of the factors is zero, it's:\(x-7=0 \rightarrow x=7\\x+3=0 \rightarrow x=-3\)