4/5 divide 2/3 i need the answer now and thank you!
Answers
Answer:
5/6 in fraction form and 1.2 in decimal form
Step-by-step explanation:
4/5 divided by 2/3 is equal to 5/6 in fraction form and 1.2 in decimal form
Related Questions
Which expression can be used to find the total number of berries in 5 baskets if there are 20 berries per basket?
CLEAR CHECK
5 berries plus 20 berries
5 baskets times 20 berries per basket
20 times 20 berries
5 times the number of baskets
Answers
Answer:
ask your teacher
Step-by-step explanation:
can someone help asap

Answers
Explanation:
Since 23 is in the hundredths and it can also be represented as 23/100, we can say twenty three hundredths
Zero point two three is not exactly mathematically correct, but most people automatically say this
Answer:
twenty three hundredths
Step-by-step explanation:
Decimals have place values just like whole numbers.
The first number after the decimal point: 0.0 is the tenths places
The second place is the hundredths.
in this number the 0 means nothing so we just have to focus on the 23
Whoever gets the question right I will mark as brainliest

Answers
Calculate volume of the prism
20 × 12 × 15
= 3600 in³
divide volume of prism with volume of container
3600 ÷ 400
= 9
9 times
determine whether or not the vector field is conservative. f(x,y) = 33x2y2i + 22x3yj
Answers
The vector field f(x,y) = 33x^2y^2i + 22x^3yj is conservative, and its potential function is φ(x,y) = 11x^3y^2 + 11x^2y^2 + C.
To determine if a vector field is conservative, we need to check if it is the gradient of a scalar function (i.e., a potential function). We can do this by taking the partial derivatives of each component with respect to their respective variables and checking if they are equal:
∂f_x/∂y = 66xy^2
∂f_y/∂x = 66xy^2
Since these partial derivatives are equal, the vector field is conservative. We can then find a potential function by integrating each component with respect to their respective variable:
φ(x,y) = 11x^3y^2 + 11x^2y^2 + C
where C is the constant of integration.
Therefore, the vector field f(x,y) = 33x^2y^2i + 22x^3yj is conservative, and its potential function is φ(x,y) = 11x^3y^2 + 11x^2y^2 + C.
Learn more about vector field
brainly.com/question/14122594
#SPJ11
Let A be some event/disease/thing you want to know about, and let "pos" mean test positive for, or evidence in favor of, A. Show that P(pos∣A)≥P(pos∣A C
)⇔LR:=P(pos∣A)/P(pos∣A C
)≥1⇔P(A∣pos)/P(A C
∣pos)≥P(A)/P(A C
), i.e., the posterior odds are higher than the prior odds.
Answers
P(pos|A) ≥ P(pos|A') is equivalent to LR ≥ 1, which is further equivalent to P(A|pos)/P(A'|pos) ≥ P(A)/P(A').
To show that P(pos|A) ≥ P(pos|A'), we can use Bayes' theorem:
P(A|pos) = P(pos|A) * P(A) / P(pos)
P(A'|pos) = P(pos|A') * P(A') / P(pos)
Dividing these two equations, we get:
P(A|pos) / P(A'|pos) = (P(pos|A) * P(A) / P(pos)) / (P(pos|A') * P(A') / P(pos))
Simplifying further:
P(A|pos) / P(A'|pos) = (P(pos|A) * P(A)) / (P(pos|A') * P(A'))
= LR * P(A) / P(A')
= P(A) / P(A') * LR
Now, let's examine the relationship between the prior odds and the posterior odds:
P(A) / P(A') is the prior odds.
P(A|pos) / P(A'|pos) is the posterior odds.
We want to show that the posterior odds are higher than the prior odds, i.e., P(A|pos) / P(A'|pos) ≥ P(A) / P(A').
From the earlier equation, we have:
P(A|pos) / P(A'|pos) = P(A) / P(A') * LR
Since LR = P(pos|A) / P(pos|A'), we can rewrite the equation as:
P(A|pos) / P(A'|pos) = P(A) / P(A') * (P(pos|A) / P(pos|A'))
Now, if P(pos|A) ≥ P(pos|A'), then the right-hand side of the equation is greater than or equal to 1. Therefore, we can conclude that P(A|pos) / P(A'|pos) ≥ P(A) / P(A').
In other words, the posterior odds are higher than the prior odds when P(pos|A) ≥ P(pos|A').
Learn more about Bayes' theorem here: https://brainly.com/question/33143420
#SPJ11
Compute the flux of F⃗ =3(x+z)i⃗ +2j⃗ +3zk⃗ through the surface S given by y=x^2+z^2, with 0≤y≤16, x≥0, z≥0, oriented toward the xz-plane
Answers
It seems there is an error in the given vector field F⃗ = 3(x+z)i⃗ + 2j⃗ + 3zk⃗ as it does not have a component along the y-axis. Please double-check the vector field or provide the correct vector field to proceed with the calculation.
To compute the flux of the vector field F⃗ = 3(x+z)i⃗ + 2j⃗ + 3zk⃗ through the surface S given by y=x^2+z^2, with 0≤y≤16, x≥0, z≥0, oriented toward the xz-plane, we can use the surface integral.
The surface integral of a vector field F⃗ over a surface S is given by the formula:
∬S F⃗ · dS = ∬S F⃗ · (n⃗ dS)
where F⃗ is the vector field, dS is the differential area vector, and n⃗ is the unit normal vector to the surface.
In this case, the surface S is given by y=x^2+z^2, with 0≤y≤16, x≥0, z≥0. We can parameterize this surface as:
r(x, z) = xi⃗ + yj⃗ + zk⃗ = xi⃗ + (x^2+z^2)j⃗ + zk⃗
To find the normal vector n⃗ to the surface, we can take the cross product of the partial derivatives of r(x, z) with respect to x and z:
n⃗ = ∂r/∂x × ∂r/∂z
= (1i⃗ + 2xj⃗) × (0i⃗ + 2zj⃗)
= -2xz i⃗ + 2zj⃗ + 2xk⃗
Now, we can calculate the flux:
∬S F⃗ · (n⃗ dS) = ∬S (3(x+z)i⃗ + 2j⃗ + 3zk⃗) · (-2xz i⃗ + 2zj⃗ + 2xk⃗) dS
= ∬S (-6x^2z - 4xz + 6xz^2 + 6xz) dS
= ∬S (-6x^2z + 2xz + 6xz^2) dS
To evaluate this integral, we need to determine the limits of integration for x, y, and z.
Since the surface is defined by 0≤y≤16, x≥0, z≥0, we have:
0 ≤ y = x^2 + z^2 ≤ 16
Simplifying the inequality, we get:
0 ≤ x^2 + z^2 ≤ 16
From this, we can see that x and z both range from 0 to 4.
Now, we can evaluate the flux:
∬S (-6x^2z + 2xz + 6xz^2) dS = ∫∫ (-6x^2z + 2xz + 6xz^2) dA
where dA is the differential area.
Integrating over the limits 0 ≤ x ≤ 4 and 0 ≤ z ≤ 4, we can calculate the flux.
However, it seems there is an error in the given vector field F⃗ = 3(x+z)i⃗ + 2j⃗ + 3zk⃗ as it does not have a component along the y-axis. Please double-check the vector field or provide the correct vector field to proceed with the calculation.
Learn more about vector from
https://brainly.com/question/28028700
#SPJ11
A 14 foot ladder is leaning against a building. The ladder makes a 45 degree angle with the building. How for up the building does the ladder reach?
Answers
Answer:
\(7\sqrt{2}\)
Step-by-step explanation:
Use trigonometry.
sin 45 degrees = x/14
plug in values and you get x = \(7\sqrt{2}\)
Answer:
72
Step-by-step explanation:
Need help asapp!!
- x < 5
- x > 5

Answers
Answer: it A
Step-by-step explanation: Hope this help :D
Is 5/18 a rational number ?
Answers
Answer:
5/18 is a rational number because a rational number is any integer,fraction terminating decimal,or repeating decimal.
5/18 is rational number.
What is Rational Number?The word "ratio" is where the word "rational" first appeared. Rational numbers are therefore closely tied to the idea of fractions, which stand for ratios. In other terms, a number is a rational number if it can be written as a fraction in which the numerator and denominator are both integers.
Any number of the form p/q, where p and q are integers and q is not equal to 0, is a rational number. The letter Q stands for the set of rational numbers. Look at the following illustration to see what a rational number looks like.
Given:
5/18
For rational we need to first divide the fraction and then check whether the fraction is a decimal or not.
Or if it is a decimal then it is terminating or non terminating
5/18 = 0.2777777777777778
Hence, it is terminating because rational number is any integer, fraction terminating decimal or repeating decimal.
Learn more about rational number here:
https://brainly.com/question/24398433
#SPJ2
✨ Easy points if you know how to do slope well ✨

Answers
Answer:
I believe it's A
Step-by-step explanation:
Answer:
its y=x
Step-by-step explanation:
Find x if the average of 18, 12, 11, 10, and x is 12
Answers
Step-by-step explanation:
to fine the average add all the numbers and divide the 5
18+12+11+10+12/5 =53.4
-6y=-4x+24 use intercepts to graph the line described by each equation
Answers

Write the expression using exponents.
3 × 3 × 3 × 3
A. 33
B. 34
C. 43
D. 35
Answers
Answer:
B
Step-by-step explanation:
What is the slope of the line?

Answers
Answer:
solpe=-1
Step-by-step explanation:
slope = (y2-y1/X2-X1)
(2,0) (0,2)
(2-0/0-2)
2/-2
slope= -1
calculate the number of waffles produced if you start with 15 eggs, assuming you have enough of all other ingredients? given: 4 cups flour 6 eggs 2 tbsp oil 8 waffles
Answers
The number of waffles can be made from 15 eggs are, 20 waffles.
the waffles can be calculates as follows
4 cups of fluor + 6 eggs +2 tbsp oil = 8 waffles
we need 6 eggs to make 8 waffles
So, the waffles can we make from 15 eggs = \(\frac{8}{6} X 15 = 20\) waffles
Hence, the number of waffles can be made from 15 eggs are 20 waffles.
Learn more about this equation at
https://brainly.com/question/14275434
#SPJ1
if c(x)= 5/x-2 and d(x)=x+3, what is the domain of (cd)(x)
Answers
Answer:
Step-by-step explanation:
cd(x) would equal c(x) multiplied by d(x) so we get \(\frac{5(x+3)}{x-2}\\\) = \(\frac{5x+15}{x-2}\\\).
The domain of \(\frac{5x+15}{x-2}\) is anything except 2, so the domain of (cd)(x) is (-inf, 2) U (2, inf).
a local news outlet reported that 56% of 600 randomly sampled kansas residents planned to set off fireworks on july 4th. compute the 98% confidence interval for the true proportion.
Answers
The 98% confidence interval for the true proportion is (0.506, 0.614).
Given that a local news outlet reported that 56% of 600 randomly sampled Kansas residents planned to set off fireworks on July 4th and we need to compute the 98% confidence interval for the true proportion.
The formula to find the confidence interval is given by;
\(CI = \hat{p} \pm z_{\alpha/2} \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
Where,
\(\hat{p}\) = Sample proportion\(n\)
= Sample size\(z_{\alpha/2}\)
= Critical value for the confidence level\(\alpha\)
= Level of significance
Let's put the given values in the above formula:
\(\hat{p} = 56\%
= 0.56\)\(n
= 600\)\(\alpha
= 0.02\) (As the level of significance is 1 - 0.98)\(z_{\alpha/2}\)
= 2.33 (From standard normal distribution table)N
ow, we will compute the confidence interval by putting the above values in the formula;
\(\begin{aligned}CI
= \hat{p} \pm z_{\alpha/2} \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\
= 0.56 \pm 2.33 \times \sqrt{\frac{0.56(1-0.56)}{600}} \\
= 0.56 \pm 0.054 \\
= (0.506, 0.614) \end{aligned}\)
Therefore, the 98% confidence interval for the true proportion is (0.506, 0.614).
Know more about 98% confidence interval here:
https://brainly.com/question/17097944
#SPJ11
Help please I don’t understand
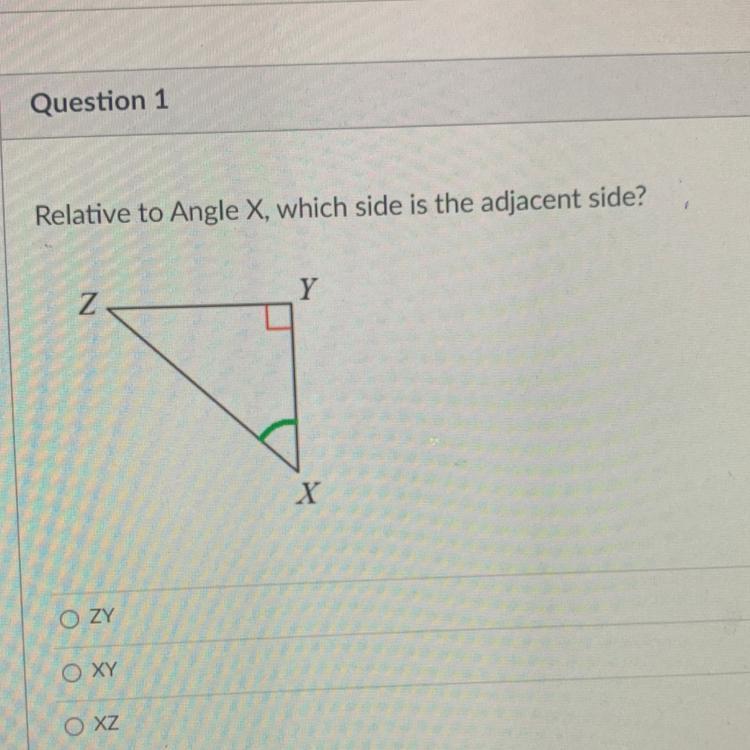
Answers
Answer:
It is xy
Step-by-step explanation:
Answer:
XY
Step-by-step explanation:
omit the hypotenuse (XZ) since it's always hypotenuse while the adjacent and opposite sides vary.
hypotenuse cannot be both adjacent and hypotenuse at the same time.
The table below represents a quadratic function. Use the data in the table to
determine the domain and range of the function.
x
-1
0
1
4
y
5
3
5
35

Answers
The domain is all real numbers and the Range is y ≥ 3.The correct answer is option A.
To determine the domain and range of the quadratic function based on the given table, let's analyze the values.
Domain represents the set of possible input values (x-values) for the function.
Range represents the set of possible output values (y-values) for the function.
From the given data:
x = -1, 0, 1, 4
y = 5, 3, 3, 5, 35
Looking at the x-values, we can see that the function has values for all real numbers. Therefore, the domain of the function is "all real numbers."
Now, let's consider the y-values. The minimum value of y is 3, and there are no y-values less than 3.
Additionally, the maximum value of y is 35. Based on this information, we can conclude that the range of the function is "y ≥ 3" since all y-values are greater than or equal to 3.
Therefore, the correct answer is:A. Domain: all real numbers
Range: y ≥ 3
For more such questions on Range,click on
https://brainly.com/question/30389189
#SPJ8
The probable question may be:
The table below represents a quadratic function. Use the data in the table to determine the domain and range of the function.
x= -1,0,1,4
y= 5,3,3,5,35
A. Domain: all real numbers Range: y ≥3
B. Domain: all real numbers
Range: x≥0
c. Domain: all real numbers
Range: y ≥0
D. Domain: all real numbers
Range: y ≤3
Do the ratios 60:45 and 10:9 form a proportion?
Answers
Comparing the two simplified ratios, 4:3 and 10:9, we see that they are not equal, so the ratios 60:45 and 10:9 do not form a proportion.
How are proportions determined?We must examine whether the cross-products are equal in order to determine whether the ratios of 60:45 and 10:9 constitute a proportion.
60 x 9 = 540 is the cross product of 60 and 9.
45 x 10 = 450 is the cross product of 45 and 10.
The cross-products are not equal, hence the ratios of 60:45 and 10:9 do not constitute a proportion (540 is not equal to 450, for example).
Simplifying two ratios to their simplest form is another technique to determine if they constitute a proportion.
By dividing both components by their greatest common factor, which is 15, the ratio 60:45 can be reduced to 4:3.
The 10:9 ratio has already reached its lowest point.
Learn more about Proportions here:
brainly.com/question/11897796
#SPJ9
is 49.080 equal to lesser than or greater than 49.08
Answers
Answer:
there equal
I think but I'm not sure
HELP PLS!!!!!
A company produces individually wrapped spherical cookies. The minimum amount of wrapping material needed to
cover a cookie, assuming no edges overlap, is 314 square inches. What is the diameter of one cookie?
5 in
10 in
20 in
25 in
Answers
Answer:
10 in
Step-by-step explanation:
r^2= 314/3.14
r^2=100
r=10 in
hope i helped!
Between 2010 and 2015 the average rate of inflation was about 3.2% per year. If a cart of groceries cost $150 in 2010 what will it cost in 2015
Answers
Answer:
$175.59
Explanation:
If the average rate of inflation was 3.2% per year, we can say that each year the cost of the cart increase by 3.2%, so the cost in 2011 was:
$150 + $150(0.032)
= $150(1 + 0.032)
= $150(1.032)
= $154.8
Because $150 was the cost in 2010 and 3.2% is equal to 0.032. Then, the cost in 2012 was:
$154.8 + $154.8(0.032)
= $154.8(1 + 0.032)
= $154.8(1.032)
= $159.75
In the same way, the cost in 2013, 2014 and 2015 will be:
In 2013: $159.75(1.032) = $164.87
In 2014: $164.87(1.032) = $170.14
In 2015: $170.14(1.032) = $175.59
Therefore, the cost in 2015 will be $175.59
Simplify
55-63.810
5-6-8°
Answers
Answer:
Step-by-step explanation:

Identify the variable terms, constant terms, and coefficients for each expression.
EXPRESSION
VARIABLE TERMS CONSTANT TERMS COEFFICIENTS
1.
14w- 3w
2.
-2a+ 9-5a
3.
8m-2-10+ m
4.
-2p-17 +6p - p+4
5.
14x – 3y + 5y - 26-7x
6.
-6C +18-15d + C-11-3c
Answers
1. 14w - 3w
Variable term: 14w, -3w
Constant term: None
Coefficient: 14, -3
2. -2a + 9 - 5a
Variable term: -2a, -5a
Constant term: 9
Coefficient: -2, -5
3. 8m - 2 - 10 + m
Variable term: 8m, m
Constant term: -2, -10
Coefficient: 8, 1
4. -2p - 17 + 6p - p + 4
Variable term: -2p, 6p, -p
Constant term: -17, 4
Coefficient: -2, 6, -1
5. 14x - 3y + 5y - 26 - 7x
Variable term: 14x, -3y, 5y, -7x
Constant term: -26
Coefficient: 14, -3, 5, -7
6. -6C + 18 - 15d + C - 11 - 3c
Variable term: -6C, -15d, C, -3c
Constant term: 18, -11
Coefficient: -6, -15, 1, -3
In each expression, variable terms are the terms that contain variables (letters representing unknowns), constant terms are the terms that do not contain variables, and coefficients are the numbers multiplying the variables. Let's identify the variable terms, constant terms, and coefficients for each expression:
In each expression, the variable terms consist of the terms containing variables, the constant terms are the terms without variables, and the coefficients are the numbers multiplying the variables.
for more such questions on variables
https://brainly.com/question/25223322
#SPJ8
7
9. Write the equation of a line that goes through the
point (-2,9) perpendicular to the line y = 6.
Answers
Answer:
x = -2
Step-by-step explanation:
Given the point, (-2, 9) and the linear equation of a horizontal line, y = 6:
The linear equation of a horizontal line with a slope of zero (m = 0) is y = b, for which the y-intercept is (0, b). Perpendicular lines comprise of the intersection of two lines forming 90° angles.
Since we are given the equation of a horizontal line, then we can assume that the line that intersects a horizontal line must be a vertical line in order to form perpendicular lines.
The linear equation of a vertical line with an undefined slope is x = a, for which the x-intercept is (a, 0). Vertical lines have an undefined slope because these lines do not have any horizontal change. Thus, when you try to solve for its slope, the denominator will have a difference of 0, making the mathematical operation undefined.
We can use the x-coordinate of the given point, (-2, 9), to formulate an equation for a vertical line: x = -2.
Therefore, the equation of the line that goes through y = 6 is x = -2.
Attached is a screenshot of the graph of both equations, y = 6 and x = -2, showing that their intersection form 90° angles, making them perpendicular lines.

Find the future value of an account compounded quarterly at 5.67% for 4 years, if $7,000 was deposited into the account.
Answers
Step 1) : We know that,
\(\begin{cases}P = 7000& \\r = 5.6 \% & \\ n = 4 & \\ t = 4 & \end{cases}\)
Step 2) : Formulate and Substitute:
\(Substitute\begin{cases}P = 7000& \\ r = 5.6 \% & into \: formula \\ n = 4 & \\ t = 4 & \end{cases}\)
\(\bf\longrightarrow{F = P * (1 + \frac{r}{n} )^{(n*t)}} \)
Put the values according to the formula:
\(\bf\longrightarrow{F = 7000 * (1 + \frac{ \frac{5.67}{100} }{4} )^{(4*4)}}\)
Step 3) : Evaluate the equation/expression:
\(\bf\longrightarrow{8768.1}\)
At a local manufacturing plant, employees must complete new machine set ups within 30 minutes. New machine set-up times can be described by a normal model with a mean of 22 minutes and a standard deviation of four minutes.
The typical worker needs five minutes to adjust to their surroundings before beginning their duties. What percent of new machine set ups are completed in less than 25 minutes?
A. Approximately 25%
B. Approximately 68%
C. Approximately 22.7%
D. Approximately 77,3%
Answers
The correct option is (D). Approximately 77.3% of new machine set ups are completed in less than 25 minutes.
Given a local manufacturing plant, employees must complete new machine set ups within 30 minutes.
The new machine set-up times can be described by a normal model with a mean of 22 minutes and a standard deviation of four minutes. The typical worker needs five minutes to adjust to their surroundings before beginning their duties.
To find the percentage of new machine set ups completed in less than 25 minutes, we need to calculate the z-score. For this, we will use the formula:
z = (X - μ) / σ
where X = 25 minutes, μ = 22 minutes, and σ = 4 minutes
z = (25 - 22) / 4z = 0.75
We can now look up the percentage of the area under the normal distribution curve that corresponds to z = 0.75. Using a standard normal distribution table, we find that the area to the left of z = 0.75 is approximately 0.7734.
So, the percentage of new machine set ups completed in less than 25 minutes is approximately 77.34%.
Therefore, the correct option is (D).Approximately 77.3% of new machine set ups are completed in less than 25 minutes.
Learn more about normal distribution curve here:
https://brainly.com/question/30783928
#SPJ11
A can of soda is placed inside a cooler. As the soda cools, its temperature C (t) in degrees Celsius after t minutes is given by the following exponential function.
C (t) = 19 (0.96)
Find the initial temperature.
__ C
Does the function represent growth or decay?
O growth
O decay
By what percent does the temperature change each minute?
__%
Answers
The temperature decreases by 4% each minute.
What is the exponential decay
Exponential decay is a process in which a quantity decreases over time and the rate of decrease is proportional to the current value of the quantity. This means that as the quantity decreases, the rate of decrease slows down.
I believe there is an error in the given function. It seems to be missing the exponent for 0.96. Assuming that it should be "\(C(t) = 19(0.96)^t\)", I can provide the following solutions:
The initial temperature is the temperature when t = 0. Plugging in t = 0 into the function, we get:
\(C(0) = 19(0.96)^0 = 19(1) = 19\)
Therefore, the initial temperature is 19 degrees Celsius.
The function represents decay because the base of the exponential term (0.96) is between 0 and 1, causing the function to approach 0 as time goes on.
The percent change in temperature each minute can be calculated using the following formula:
Percent Change = (New Value - Old Value) / Old Value x 100%
For each minute that passes, the temperature decreases by a factor of 0.96. Therefore, the new temperature is 0.96 times the old temperature. Using the initial temperature of 19 degrees Celsius, we can calculate the percent change in temperature each minute as follows:
Percent Change = \((0.96 * 19 - 19) / 19 * 100%\)
= -4%
Hence, the temperature decreases by 4% each minute.
To learn more about exponential decay, Visit
https://brainly.com/question/27822382
#SPJ1
Plz help i need it asap

Answers
Answer:
Comment section got full
that is why it's not letting you comment.