4(5x+5) = - 24 + 4
I don't know how to solve this
Answers
Answer: x=-2
Step-by-step explanation:
4(5x+5) = - 24 + 4
20x+20=-24+4 ==> Distributive Property
20x+20-20=-24+4-20
20x=-20-20
20x=-40
x=-2
Related Questions
Let P(x) be a predicate in the domain consisting of just the numbers 0 and 1. Let p be the statement P(0) and let q be the statement P(1).
(a) Write (∀x)P(x) as a propositional logic formula using p and q.
(b) Write (Ǝx)P(x) as a propositional logic formula using p and q.
(c) In this situation, which derivation rule from propositional logic corresponds to the universal and existential negation rules of predicate logic?
Answers
(∀x)P(x) can be written as p ∧ q, (Ǝx)P(x) can be written as ¬p ∨ ¬q, and the universal and existential negation rules of predicate logic correspond to the DeMorgan's law of propositional logic, which states that ¬(p ∨ q) = ¬p ∧ ¬q.
a) The statement (∀x)P(x) states that P(x) is true for all x in the domain, which consists of just 0 and 1. So, if P(0) is true, represented by p, and P(1) is true, represented by q, then (∀x)P(x) is true. Therefore, (∀x)P(x) can be written as p ∧ q.
b) The statement (Ǝx)P(x) states that P(x) is true for at least one x in the domain, which consists of just 0 and 1. So, if either P(0) is true, represented by p, or P(1) is true, represented by q, then (Ǝx)P(x) is true. Therefore, (Ǝx)P(x) can be written as p ∨ q.
c) The negation of (∀x)P(x), represented as ¬(∀x)P(x), is equivalent to the negation of (∀x)P(x) in predicate logic, represented as (Ǝx)¬P(x). This corresponds to DeMorgan's law of propositional logic, which states that ¬(p ∧ q) = ¬p ∨ ¬q.
Similarly, the negation of (Ǝx)P(x), represented as ¬(Ǝx)P(x), is equivalent to the negation of (Ǝx)P(x) in predicate logic, represented as (∀x)¬P(x). This corresponds to DeMorgan's law of propositional logic, which states that ¬(p ∨ q) = ¬p ∧ ¬q.
To know more about DeMorgan's law, here
https://brainly.com/question/13265106
#SPJ4
What's 2+5^3, and how exactly would I solve it
Answers
The result of the expression 2 + 5^3 is 127.
To solve the expression 2 + 5^3, you need to follow the order of operations, which is often remembered using the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division from left to right, Addition and Subtraction from left to right).
In this case, the exponentiation should be performed first.
Step 1: Calculate 5^3
5^3 means raising 5 to the power of 3, which is equivalent to multiplying 5 by itself three times: 5 * 5 * 5 = 125.
Step 2: Add 2 to the result from Step 1.
2 + 125 = 127.
Therefore, the result of 2 + 5^3 is 127.
For more such questions on result , Visit:
https://brainly.com/question/29248277
#SPJ11
Amanda is going to build some large wooden storage boxes. The boxes are shaped like rectangular prisms, as shown below. She wants to cover all the sides of each box with special wallpaper. If she has a total of of wallpaper, how many boxes can she cover?
Answers
The number of boxes that Amanda can cover with W square inches of wallpaper will be equal to W/2(lw + lh + wh).
Let's assume that Amanda wants to build n wooden storage boxes. All of these boxes are shaped like rectangular prisms, as shown in the image below.
She wants to cover all the sides of each box with special wallpaper. If she has a total of W square inches of wallpaper, we need to find out how many boxes she can cover. Let's solve this problem mathematically.
Mathematical Solution:
Each rectangular prism has six sides (faces). If we want to cover all the six sides of a rectangular prism with special wallpaper, we need to find the total surface area of that rectangular prism. Therefore, the surface area of each rectangular prism can be calculated by the formula:
Surface Area = 2lw + 2lh + 2wh,
where l, w, and h are the length, width, and height of the rectangular prism, respectively.
We know that Amanda has W square inches of wallpaper to cover all the boxes. Therefore, the total surface area of n boxes will be:
n × Surface Area = W.
Substituting the value of the Surface Area, we have:
n × (2lw + 2lh + 2wh) = W
2n(lw + lh + wh) = W
n(lw + lh + wh) = W/2
n = W/2(lw + lh + wh).
To learn more about : number
https://brainly.com/question/24644930
#SPJ8
4. Find the average value of the given function on the given interval. Then find all points c whose existence is guaranteed by the Mean Value Theorem for Integrals. (a) f(x) = x2 – 8x + 10 on (2, 5] (b) f(x) = Vx on [1, 16]
Answers
The average value of the given function on the given interval is = 7/2 and 6.25 respectively
What is Average?
The middle number, which is obtained by dividing the sum of all the numbers by the variety of numbers, is the average value in a set of numbers. To calculate the average of a set of data, add up all the values and divide the result by the total number of values.
(a) f(x) = x2 – 8x + 10
f = 1/b-a \(\int\limits^b_a {f(n)} \, dx\)
f = 1/5-2 \(\int\limits^5_2 {x^{2} -8x+10} \, dx\)
Here, a=2
b=5
f(x) =x2 – 8x + 10
f = 1/3 (x³/3 - 8x²/2+10x)5/2
f = -25/9 -20/9
f = -45/9
= -5
Mean Value Theorem
If f(x) = continous on (a, b)
If f(x) = differentiable on (a, b)
Then f(c) = f(b) -f(a)/b-a
were c∈ (a,b)
Here, f(c) = f(-5)-f(2)/5-2
f(c) = -5+2/3
f(c) = -1 ......................(1)
Here, f(x) = x²-8x+10
f(c) = c²-8c+10
f(x) = 2c-8...................(2)
equating 1&2
2c -8 = -1
2c = -1 +8
c = 7/2
c∈ (2,5)
(b) f(x) = Vx on [1, 16]
f = \(\sqrt{x}\) on (1 ,16)
f= 1/b-a \(\int\limits^b_a {f(n)} \, dx\)
f = 1/16-1 \(\int\limits^6_1 {\sqrt{x} } \, dx\)
f = ( 2x (3/2)/45)₁¹⁶
f = 128/45-2/45
f = 126/45
= 14/5
Mean Value Theorem
f(x) = \(\sqrt{x}\)
f(c) =\(\sqrt{c}\)
f(c) = 1/2\(\sqrt{c}\)....................(1)
we know that
f(c) = f(b)-f(a)/b-a
f(c) = f(16)-f(1)/16-1
f(c) = \(\sqrt{16}\) -\(\sqrt{1}\)/15
f(c) = 4-1/15
= 3/15.....................(2)
Equating (1) and (2)
1/2\(\sqrt{c}\) = 3/15
2\(\sqrt{c}\) = 15/3
2\(\sqrt{c}\) = 5
\(\sqrt{c}\) = 5/2
c = (5/2)²
=25/4
c≅ 6.25
6.25 = (1 ,16)
The average value of the given function on the given interval is = 7/2 and 6.25 respectively
To learn more about Average visit
brainly.com/question/27193544
#SPJ4
HELP PLEASE
Which combination of integers can be used to generate the Pythagorean
triple 5,12,13)?
A. X = 1, y = 3
B. X = 3.y = 2
C. X = 3.y = 4
D. X = 2 y = 2
Answers
step by step explanation
Select the values that make the inequality <-3 true. Then write
an equivalent inequality, in terms of t.
(Numbers written in order from least to greatest going across.)
n
2
5
8
3
6
9
Equivalent Inequality: t
◄►
4
7
t
-2
10
Answers
Answer:
none, because all of them are greater than -3
m ANGLE 1 = 3x-5 and m ANGLE 2 = 2x+7 find the values of angle 1 and 2
Answers
Answer: Angle one equals -15, and angle two equals 14, if the +7 equals a positive seven.
Step-by-step explanation:
There are more negatives than positives, so we make the ending answer negative, giving us -15. And the second one is simple multiplication, you double the 7 times two, or vice versa.
Hope this helps!
The analysis of total variability into between-treatments and within-treatments variability is the same for a repeated-measures ANOVA and an independent-measures ANOVA.TrueFalse
Answers
The given statement ,the analysis of total variability into between-treatments and within-treatments variability is the same for a repeated-measures ANOVA and an independent-measure ANOVA is true.
The first stage of the repeated-measures ANOVA is identical to the independent-measures analysis and splits the overall variability into two components: between-treatments and within-treatments
Measurements that are repeated ANOVA is the extension of the dependent t-test and is the equivalent of one-way ANOVA for related, rather than independent, groups.
A repeated measures ANOVA is often referred to as a within-subjects ANOVA or ANOVA for correlated samples. The term "responsibility" refers to the act of determining whether or not a person is responsible for his or her own actions.
To learn more about ANOVA
brainly.com/question/7192786
#SPJ4
PLEASE HELP ME I AM CRYING AND NEED AN ANSWER BC THIS IS DUE

Answers
Answer:
334 square inches
Step-by-step explanation:
Base terms
Length, l : 11
Width, w : 7
Height, h : 5
S=2(lw+lh+wh)
S= 2(11*7 + 11*5 + 7*5)
Surface area, SA : 334.00
Cuboid is a simple figure. It has three dimensions - width, length and height.
S=2(lw+lh+wh)
Answer:
340in squared
Step-by-step explanation: Surface area formula: add areas of all faces.
Which is not a true statement about the figures shown below
Answers
Answer:That is no thing shown below
Step-by-step explanation:
Answer:
I wish I could help you but you didn't attach a picture.
Solve the question below:

Answers
Answer:
x = 15
Step-by-step explanation:
3x+1+4x-3 = 103
7x = 105
x = 15
Define associative property
Answers
Answer:
the way in which factors are grouped in a multiplication problem does not change the product.
Step-by-step explanation:
find the value of ...B

Answers
Answer:
b=–2
Step-by-step explanation:
we've got:
(3+bx)⁵===> b⁵x⁵+15b⁴x⁴+90b³x³+720b²x²+405bx+243
and we've also got the coefficient of x³ as –720
90b³=–720===> b³=–8===> b=–2
Find Trig Ratios (with Radicals)

Answers
Answer:
the answer is 45 + 5-75 is equals to 30 +5
please help with the problem below

Answers
Answer:
ow that so hard
Step-by-step explanation:
wait let me see the answer i well search it
what is the Smallest numbers :
p = x^2 + 2x +2 / x+1 (x>-1)
t= 1/x + 4/1-x (0
Answers
Answer:
I exactly don't know the answer
procedures that help organize or describe data collected from a sample or a population are called . group of answer choices a. inferential statistics b. analytical variables c. dependent variables d. descriptive statistics
Answers
Procedures that help organize or describe data collected from a sample or a population are called Descriptive statistics.
Hence, option D is correct answer.
Descriptive statistics and examples: what are they?Data can be meaningfully and effectively described or summarised using descriptive statistics. For instance, knowing that everyone in our scenario wore blue shoes wouldn't be helpful. It would be helpful to know how evenly distributed their anxiety scores were. Measures of central tendency and measurements of variability make up descriptive statistics (spread).
The mean, median, and mode are measurements of central tendency, while the standard deviation, variance, minimum and maximum variables, kurtosis, and skewness are measures of variability.
Why do we utilise descriptive statistics?
In order to emphasise potential correlations between variables and to give basic information about the variables in a dataset, descriptive statistics can be helpful for both of these aims. The three most used descriptive statistics, which represent the following three variables: graphical/illustrative techniques.
Learn more about the Statistics here: https://brainly.com/question/218301
#SPJ1
Parmesan cheese was on sale for $13.60 per pound. Wesley bought a piece of parmesan cheese that weighed 1 ⅛ pounds
how much did he pay and if you can explain
Answers
Answer:
Step-by-step explanation:
Given Parmesan cheese was on sale for $13.60 per pound
Welsey bought a piece of the parmesan cheese that weighted \frac{11}{8} pounds
we need to spend$13.60 for 1 pound
for 11/8 pound
11/8 x 13.60= 18.72
So Wesley need to spend $18.70 to get the Parmesan cheese.
A house was valued at $238,000. Over several years, the value decreased by 16%, giving the house a new value.
(a) Fill in the blank to write the new value in terms of the old value.
Write your answer as a decimal.
New value = 1 x Old value
(1) Use your answer in part (a) to determine the new value.
New value: 0

Answers
Answer:
The new value of the house after the 16% decrease would be $199,920.
Step-by-step explanation:
Given that a house was valued at $ 238,000, and over several years, the value decreased by 16%, giving the house a new value, to determine the new value the following calculation must be performed:
238,000 - (238,000 x 0.16) = X
238,000 - 38,080 = X
199.920 = X
Thus, the new value of the house after the 16% decrease would be $ 199,920.
A man walks up 800m road AB which slopes at 10.2 to the horizon. He then walks 300m down road BC, which is at 6.3 to the horizon. The horizon is parallel to AD and BF perpendicular to AD. Find the length of CD
Answers
The length of CD is approximately 27.931 meters.
To find the length of CD, we can use the concept of similar triangles and trigonometric ratios.
Let's start by drawing a diagram to visualize the situation:
A----------B
/ /
/ /
/ /
D----------C
|
|
|
F
We are given that road AB slopes at 10.2 degrees to the horizon and road BC slopes at 6.3 degrees to the horizon. From the diagram, we can see that angle DAF is the same as the slope angle of road AB (10.2 degrees), and angle DCF is the same as the slope angle of road BC (6.3 degrees).
Now, we can set up the following trigonometric equations using the given information:
tan(10.2 degrees) = CD / AD (equation 1)
tan(6.3 degrees) = CD / BF (equation 2)
Since AD and BF are perpendicular, we can consider them as vertical heights. Let's calculate the lengths of AD and BF.
For road AB, we can use the definition of tangent:
tan(10.2 degrees) = height AB / length AB
Solving for the height AB, we have:
height AB = tan(10.2 degrees) * length AB
height AB = tan(10.2 degrees) * 800m
height AB ≈ 147.294m
Similarly, for road BC:
height BC = tan(6.3 degrees) * length BC
height BC = tan(6.3 degrees) * 300m
height BC ≈ 33.706m
Now, we can substitute these values into equations 1 and 2:
tan(10.2 degrees) = CD / 147.294m (equation 1)
tan(6.3 degrees) = CD / 33.706m (equation 2)
Solving equation 1 for CD:
CD = tan(10.2 degrees) * 147.294m
CD ≈ 27.931m
Therefore, the length of CD is approximately 27.931 meters.
for such more question on length
https://brainly.com/question/20339811
#SPJ8
if sin= 3/4 what are the values of cos 0 and tan 0

Answers
Answer:
Your choice is correct
Step-by-step explanation:
The first choice
Annual students fees at university rose from about $6,000 in 2000 to about $15,000 in 2014. Find the percent increase
Answers
Answer: 150 percent.
Step-by-step explanation:
The problem asks for the percent increase in the annual student fees from 2000 to 2014.
First, we need to know how to find a percent increase.
The percentage change formula is
(Increase in amount) / (Original amount) * 100
Using this formula, we can solve this problem.
Since the fee in 2000 was $6000 and the fee in 2014 was $15000, we can find the increase in fees.
Increase in fees = 15000-6000 == 9000
Next, let's use the formula to find the answer.
Percentage Increase = (Increase in fees) / (Original amount) * 100
= 9000 / 6000 * 100
= 150
Therefore, the answer is 150 percent.
each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
An office manager orders one calculator or one calendar for each of the office's 60 employees. Each calculator costs $15, and each calendar costs $10. The entire order totaled $800.
Part A: Write the system of equations that models this scenario. (5 points)
Part B: Use substitution method or elimination method to determine the number of calculators and calendars ordered. Show all necessary steps. (5 points)
Answers
The system of equations is.
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
And the solutions are y = 50 and x = 10.
How to write and solve the system of equations?Let's define the two variables:
x = number of calculators.y = number of calendars.With the given information we can write two equations, then the system will be:
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
Now let's solve it.
We can isolate x on the first to get:
\(\text{x} = 60 - \text{y}\)
Replace that in the other equation to get:
\(15\times(60 - \text{y}) + 10\text{y} = 800\)
\(-2\bold{y} = 900 - 800\)
\(-2\bold{y} = 100\)
\(\text{y} = \dfrac{100}{-2} = \bold{50}\)
Then \(\bold{x=10}\).
Therefore, the solutions are y = 50 and x = 10.
Learn more about systems of equations at:
https://brainly.com/question/31812807
15. This table shows the average high temperature, in °F, recorded in Savannah, GA and Atlanta, GA, over a seven day period.
Day
1
2
3
4
5
6
7
Temperature in °F, in Savannah, GA
85
87
81
79
80
91
90
Temperature in °F, in Atlanta, GA
76
73
80
78
77
81
79
Which conclusion can be drawn from the data?
A. The lower quartile for the temperatures in Savannah is lower than the lower quartile for the temperatures in Atlanta.
B. The inter-quartile range of the temperatures is the same for both cities.
C. The mean and median temperatures of Savannah were higher than the mean and median temperatures of Atlanta.
D. The upper quartile for the temperatures in Atlanta was higher than the upper quartile for the temperatures in Savannah.
16. This table shows prices for four different rides at the county fair.
Ferris Wheel
TeaCups
Ring of Fire
Bumper Cars
$2. 40
$1. 35
$3. 85
$2. 00
Which is the mean absolute deviation for this set of data?
A. 2.90 B. 0.725 C. 0 D. 1.35
17. Which of the following describes the histogram provided?
A. Symmetric
B. Skewed Left
C. Skewed Right
D. Uniform
18. Which of the following sets of data is represented by the given histogram of the frequency distribution?
Histogram
5
4
y
c
n
e
u
q
e
r
F
A.
3
2
1
0
0 5 10 15 20 25 30 35 40 45 50 Miles Per Gallon
Value
0-5
5-10
10-15
15-20
20-25
25-30
30-35
35-40
40-45
45-50
Frequency
1
2
4
4
2
2
1
1
0
0
B.
Value
0-5
5-10
10-15
15-20
20-25
25-30
30-35
35-40
40-45
45-50
Frequency
0
1
2
4
4
2
2
1
1
0
C.
Value
0-5
5-10
10-15
15-20
20-25
25-30
30-35
35-40
40-45
45-50
Frequency
0
5
10
15
20
25
30
35
40
45
D.
Value
0-5
5-10
10-15
15-20
20-25
25-30
30-35
35-40
40-45
45-50
Frequency
0
1
2
3
4
5
4
3
2
1
19. A linear regression was done to relate the age of a person, x, and the number of optimal hours of sleep, y. The equation was found to be �� = −0.12�� + 11.5 with a correlation coefficient of �� = −0.86.
a) Explain what each of the parameters in the linear model represent, i.e. the -0.12 and the 11.5. b) How do you interpret the fact that the correlation coefficient is negative?
Answers
Answer:
1.35
Step-by-step explanation:
What is the difference?
-3 2/3 - (-2 1/4)
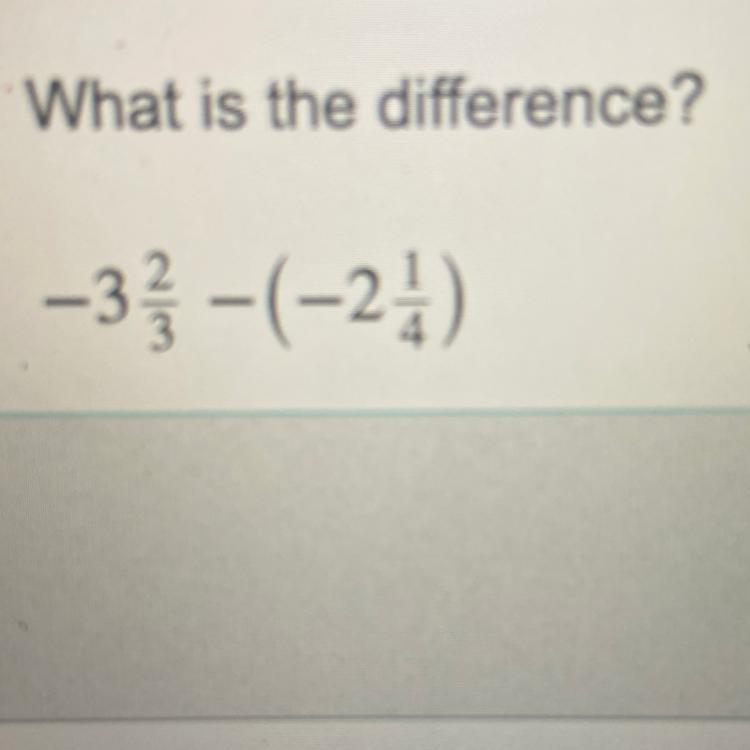
Answers
let's firstly convert the mixed fractions to improper fractions.
\(\stackrel{mixed}{3\frac{2}{3}}\implies \cfrac{3\cdot 3+2}{3}\implies \stackrel{improper}{\cfrac{11}{3}}~\hfill \stackrel{mixed}{2\frac{1}{4}} \implies \cfrac{2\cdot 4+1}{4} \implies \stackrel{improper}{\cfrac{9}{4}} \\\\[-0.35em] ~\dotfill\\\\ -\cfrac{11}{3}-\left( \cfrac{9}{4} \right)\implies -\cfrac{11}{3}+\cfrac{9}{4}\implies \cfrac{-(4)11~~ + ~~(3)9}{\underset{\textit{using this LCD}}{12}} \\\\\\ \cfrac{-44+27}{12}\implies \cfrac{-17}{12}\implies {\Large \begin{array}{llll} -1\frac{5}{12} \end{array}}\)
A store bought a dining room table at a cost of $478 and marked it up 150%. Later on, the
store marked it down 60%. What was the discount price?
Answers
Answer:
$286.80
Step-by-step explanation:
First, find the price after the 150% markup:
478(1.5)
= 717
Now, calculate the price with the 60% discount:
717(0.4)
= 286.8
= $286.80
Reuben made a shirt using 7/8yards of red fabric and 1/4yards of yellow fabric. How many more yards of red fabric did Reuben use?
Answers
Answer and Step-by-step explanation:
To find out how many more yards of red fabric Reuben used, we need to subtract the amount of yellow fabric from the amount of red fabric. Since the two fractions have different denominators, we need to find a common denominator before subtracting them. The least common multiple of 8 and 4 is 8, so we can rewrite both fractions with a denominator of 8:
7/8 - 1/4 = 7/8 - (1/4) * (2/2) = 7/8 - 2/8 = (7 - 2)/8 = 5/8
So, Reuben used 5/8 yards more red fabric than yellow fabric.
there are 70 students in the school band. 40% of them are sixth graders, 20 % are seventh graders, and the rest are eight graders. How many band members are sixth graders? How many band members are Seventh graders? What percentage of the band members are eighth graders?
Answers
Answer:
28 are 6th
14 and 7th
40% are 8th
Step-by-step explanation:
Answer:
28= 6th grader
14= 7th grader
28= 8th grader
40% were 8th graders
Step-by-step explanation:
28= 6th grader
14= 7th grader
28= 8th grader
40% were 8th graders
Summarizing allows you to focus on the important information by finding the introduction, topic sentence and
conclusion.
Please select the best answer from the choices provided
True or false
Answers
True. Summarizing allows you to focus on the important information by finding the introduction, topic sentence and conclusion.
Importance of summarySummarizing is a technique that helps to distill the main points of a text by identifying the introduction, topic sentence, and conclusion. It involves condensing the information to focus on the most important aspects and omitting unnecessary details.
This process enables the reader to grasp the core message of the text quickly and efficiently.
By summarizing, one can communicate the key ideas in a concise and clear manner, making it easier for others to understand and engage with the information presented.
More on summary can be found here: https://brainly.com/question/24839707
#SPJ1