4.7 + 2.25 find the sum
Answers
Answer:
6.95
Step-by-step explanation:
4.70 + 2.25 = 6.95
Related Questions
Evaluate the expression

Answers
The exclamation mark at the end of any number indicates a factorial. You may be able to find this button in your calculator, though where it is varies.
A factorial is the product of the integer and all of the integers below it (greater than 0).
So, 9 factorial = 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
6 factorial = 6 x 5 x 4 x 3 x 2 x 1
We can immediately eliminate the numbers that are the same on the top and bottom, since this is a fraction. That leaves us with the following multiplication problem to solve.
9 x 8 x 7 = 504
Hope this helps!
what are you guys studying?
Answers
Answer:
im study about history it was my favourite subject!
Explain the process you would use to find the area of the shaded region. Then calculate the shaded region.
You may leave your answer in terms of π or round to the nearest tenth.

Answers
The shaded region of the rectangle is 242.9 cm² and the shaded region of the sector is 7.1 square units.
What is the area of the shaded regions?Question 17) is a figure of a rectangle and two inscribed circles.
The area of a rectangle is expressed as: A = length × width
The area of a circle is expressed as: A = πr²
Where r is the radius.
To determine the area of the shaded region, we simply subtract the areas of the two circles from the area of the rectangle.
Area = ( Length × width ) - 2( πr² )
Area = ( 40 × 10 ) - 2( π × 5² )
Area = ( 400 ) - 2( 25π )
Area = 400- 50π
Area = 242.9 cm²
Area of the shaded region is 242.9 squared centimeters.
Question 18) is the a figure a sector of a circle and a right triangle.
The area of a sector is expressed as: A = (θ/360º) × πr²
The area of a triangle is expressed as: A = 1/2 × base × height
To determine the area of the shaded region, we simply subtract the areas of the triangle from the area of the sector.
Hence:
Area = ( (θ/360º) × πr² ) - ( 1/2 × base × height )
Plug in the values:
Area = ( (90/360º) × π × 5² ) - ( 1/2 × 5 × 5 )
Area = 25π/4 - 12.5
Area = 7.1
Therefore, the area of the shaded region is 7.1 square units.
Learn more about circles here: brainly.com/question/11952845
#SPJ1
For this question, I solve Q.1, but I cannot solve Q2.
Q1. Suppose that the balance of a person’s bank account in Superior, WI is normally distributed with mean $580 and standard deviation $125. Find the amount of money which would guarantee a person has more money in their account than 80% of Superior, WI residents.
Q2. For the same setup as in Problem 2, find the probability a random person from
Superior has less than $400 or more than $1000 in their bank account.
Answers
The amount of money which would guarantee a person has more money in their account than 80% of Superior, WI residents is $680 approx. The probability a random person from Superior has less than $400 or more than $1000 in their bank account is 0.9247
How to get the z scores?If we've got a normal distribution, then we can convert it to standard normal distribution and its values will give us the z score.
If we have
\(X \sim N(\mu, \sigma)\)
(X is following normal distribution with mean \(\mu\) and standard deviation \(\sigma\))
then it can be converted to standard normal distribution as
\(Z = \dfrac{X - \mu}{\sigma}, \\\\Z \sim N(0,1)\)
(Know the fact that in continuous distribution, probability of a single point is 0, so we can write
\(P(Z \leq z) = P(Z < z) )\)
Also, know that if we look for Z = z in z tables, the p-value we get is
\(P(Z \leq z) = \rm p \: value\)
Let we take:
X = The balance of a person’s bank account in Superior, WI
Then, by the given data, we have:
\(X \sim N(\mu = 580, \sigma = 125)\)
Let the amount of money which would guarantee a person has more money in their account than 80% of Superior, WI residents be X = x dollars. This is the money, below which lie 80% of Superior, WI residents, and so as their income, or values of X.
Symbolically, we have:
\(P(X < x) = 80\% = 0.8\)
Converting X to standard normal variate Z, we have:
\(Z = \dfrac{X - \mu}{\sigma} = \dfrac{X - 580}{125}\\\)
Thus, the probability statement can be rewritten as:
\(P(X < x) =0.8\\P\left( Z < z = \dfrac{x -580}{125} \right) = 0.8\)
From the z-tables, the value of Z for which the p-value comes out as between 0.84 and 0.85, let it be their average 0.845.
Thus, we get:
\(P(Z < z = 0.845) \approx 0.8\)
Thus, we get:
\(z = \dfrac{x - 580}{125} \approx 0.8\\\\x \approx 0.8 \times 125 + 580 = 680\)
Thus, the amount of money which would guarantee a person has more money in their account than 80% of Superior, WI residents is $680 approx.
Now, for second question, we need:
The probability a random person from Superior has less than $400 or more than $1000 in their bank account.
So, income of a random person from Superior is a random value of X.
So, this probability is written as:
\(P(400 < X < 1000)\)
Rewritting it, we get:
\(P(400 < X < 1000) = P(X < 1000) - P(X \leq 400)\)
Converting X to Z (standard normal variate), we get:
\(P(400 < X < 1000) = P(X < 1000) - P(X \leq 400)\\\\P(400 < X < 1000) = P\left(Z < \dfrac{1000-580}{125} \right) - P\left(Z \leq \dfrac{400-580}{125} \right)\\\\P(400 < X < 1000) = P( Z \leq 3.36) - P(Z \leq -1.44)\)
The p-value for Z = 3.36 is 0.9996
The p-value for Z = -1.44 is 0.0749
Thus, we get:
\(P(400 < X < 1000) = P( Z \leq 3.36) - P(Z \leq -1.44)\\\\P(400 < X < 1000) = 0.9996 - 0.0749 = 0.9247\)
Thus, the probability a random person from Superior has less than $400 or more than $1000 in their bank account is 0.9247
Thus, the amount of money which would guarantee a person has more money in their account than 80% of Superior, WI residents is $680 approx. The probability a random person from Superior has less than $400 or more than $1000 in their bank account is 0.9247
Learn more about z-score here:
https://brainly.com/question/21262765
#SPJ1
Two friends are collecting stuffed animals Veronica has 5 more than
Answers
Answer:
subtraction... we need the rest of the question.
Step-by-step explanation:
:/
Oki and Stephen are making bags of trail mix to sell. Oki’s trail-mix recipe requires 3 cups of nuts and 3 cups of dried fruit per bag. Stephen’s trail-mix recipe requires 4 cup of nuts and 2 cups of dried fruit per bag. Together, they want to make as many bags of trail mix as possible. They have exactly 120 cups of nuts and 90 cups of dried fruit. Find the maximum number of bags of trail mix Oki and Stephen can make together.
A. write a system of inequalities
B. Graph and find coordinates of the vertices of the feasible region.
C. Find the maximum number of bags of trail mix oki and stehpen can make. How many of each type of recipe should they make to maximize the total number of bags
Answers
Answer: Oki should make 0 bags of her recipe, and Stephen should make 30 bags of his recipe.
For vertex (15,15):
3x + 4y = 120 --> 3(15) + 4(15) = 120 --> x = 15
3x + 2y = 90 --> 3(15) + 2y = 90 -->
Step-by-step explanation: A. To find the maximum number of bags of trail mix that Oki and Stephen can make together, we can use a system of inequalities to represent the constraints:
Let "x" be the number of bags of trail mix that Oki makes and "y" be the number of bags that Stephen makes. Then we have:
3x + 4y ≤ 120 (constraint on the number of cups of nuts)
3x + 2y ≤ 90 (constraint on the number of cups of dried fruit)
x ≥ 0 (non-negative constraint for Oki's bags)
y ≥ 0 (non-negative constraint for Stephen's bags)
B. To graph the feasible region, we can start by graphing the two constraint equations as lines:
3x + 4y = 120 (line A)
3x + 2y = 90 (line B)
We can find the x and y intercepts for each line:
For line A:
When x = 0, 4y = 120, y = 30 (y-intercept)
When y = 0, 3x = 120, x = 40 (x-intercept)
For line B:
When x = 0, 2y = 90, y = 45 (y-intercept)
When y = 0, 3x = 90, x = 30 (x-intercept)
Next, we can shade the region that satisfies all of the constraints. This region is below line A and to the left of line B, and is bounded by the x and y axes.
We can find the vertices of the feasible region by finding the intersection points of the two lines and the axes. These vertices are (0,0), (0,30), (15,15), and (30,0).
C. To find the maximum number of bags of trail mix that Oki and Stephen can make together, we need to evaluate the objective function at each vertex of the feasible region, and choose the vertex that maximizes the objective function.
The objective function is the total number of bags of trail mix:
z = x + y
Evaluating at the vertices:
Vertex (0,0): z = 0 + 0 = 0
Vertex (0,30): z = 0 + 30 = 30
Vertex (15,15): z = 15 + 15 = 30
Vertex (30,0): z = 30 + 0 = 30
The maximum value of the objective function occurs at vertices (0,30) and (15,15), where z = 30 bags of trail mix.
To determine how many of each type of recipe to make, we can substitute each vertex into the two constraint equations to find the corresponding values of x and y.
For vertex (0,30):
3x + 4y = 120 --> 3x + 4(30) = 120 --> 3x = -90 --> x = -30
3x + 2y = 90 --> 3(-30) + 2(30) = 90 --> y = 15
Therefore, Oki should make 0 bags of her recipe, and Stephen should make 30 bags of his recipe.
For vertex (15,15):
3x + 4y = 120 --> 3(15) + 4(15) = 120 --> x = 15
3x + 2y = 90 --> 3(15) + 2y = 90 -->
If all real numbers satisfy the inequality, select all real numbers. If no real numbers satisfies the inequality, select no solution.
how can you tell if it's all real numbers or if no real numbers.

Answers
The solution to the inequality is x >= -2 for inequality 3x-5≥-11
The given inequality is 3x-5≥-11
Three times of x greater than or equal to minus eleven
x is the variable
3x - 5≥ -11:
Adding 5 to both sides, we get:
3x ≥ -6
Dividing both sides by 3, we get:
solution is x≥-2
Therefore, the solution to the inequality is x >= -2.
To learn more on Inequalities click:
https://brainly.com/question/28823603
#SPJ1
Andrew can run the forty yard dash in 1/2 the time that Brett can. If the sum of the two boys' times is 16.2 seconds, how many seconds does it take Brett to run the forty yard dash?
Answers
What is the inverse of the statement "If two triangles are not similar, their corresponding angles are not congruent"?
Answers
Answer:
Step-by-step explanation:
I could be wrong but I believe the answer is: if two triangles ARE similar, their corresponding angles ARE congruent.
A rock is dropped down from the top of a 500-foot cliff After 1 second, the rock is traveling 32 feet per second. After 3 seconds, the rock is traveling 96 feet per second a. Assume that the relationship between time, t, and speed, s, is linear and write an equation describing this relationship. Use ordered pairs of the form (time, speed) b. Use this equation to determine the speed of the rock 6 seconds after it is dropped. .. a. Let s represent speed and t represent time. The equation describing the relationship between speed and time is s = 32 (Simplify your answer. Use integers or fractions for any numbers in the expression.) b. The speed of the rock 6 seconds after it was dropped is 2241 ft/sec
Answers
Answer:
school! 678
Step-by-step explanation:
Which statement is not correct regarding "Gram Sabha"?
functions at the village level are like state legislature at the state level.
For keeping business rocords, every three mouths of a year is called a quater. How many months are equal to three-quaters of a year? Explain how you found your answer.
Answers
Answer:
9 months
Explanation:
3 times 3 is nine
If one quarter is 3 months. 3 of these quarters would have 9 months all together.
:
20
Linear Regression
9. The table below shows the average price of a movie ticket during certain years.
year 2002 2003 2004 2005 2006 2007
2008
price 5.80 6.03 6.21 6.41
6.55 6.88 7.18
2009
7.35
a) Find the regression equation.
b) During what approximate year will the price of a
movie ticket reach $157
Answers
can you provide a screenshot?
HELP LAST ATTEMPT MARKING AS BRAINLIEST

Answers
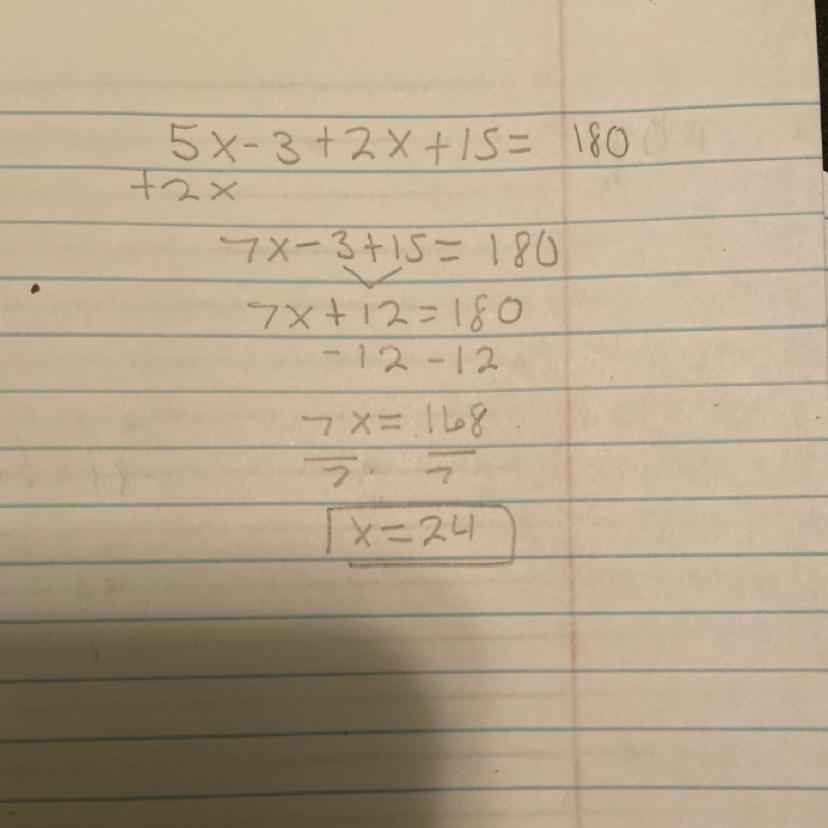
2. In AKLM, m = 5.9 cm, k = 7.1 cm and of 1, to the nearest 10th of a centimeter.

Answers
The length of side KL is approximately 4.8 cm.
To solve this problem, we can use the Law of Sines, which states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is equal for all sides of the triangle. In other words:
a/sin(A) = b/sin(B) = c/sin(C)
Where a, b, and c are the lengths of the sides of the triangle, and A, B, and C are the measures of the angles opposite those sides.
Using the Law of Sines, we can set up the following proportion:
l/sin(L) = m/sin(M)
Where l is the length of side KL, L is the measure of angle KLM (which is 72 degrees), m is the length of side LM, and M is the measure of angle KML (which we can find by subtracting L from 180 degrees).
M = 180 - L
= 180 - 72
= 108 degrees
Now we can substitute the given values into the proportion and solve for l:
l/sin(72) = 5.9/sin(108)
l = sin(72) * (5.9/sin(108))
≈ 4.8 cm (rounded to the nearest 10th of a centimeter)
For more question on length click on
https://brainly.com/question/28322552
#SPJ11
A photographer has enough liquid toner for sixty 4 in. by 8 in. prints. How many 11 in. by 14 in. prints will this amount cover?
(The toner covers the area of the print: Area=Length×Width)
The toner will cover ___ ( 13,11, 12, 48) prints of size 11 in. by 14 in.
Answers
Answer:
About 12 prints in 11×14
Step-by-step explanation:
The area of the 4×8 print is 32 in².
60 × 32= 1960
Divide by the area of an 11×14, 154 in²
1960/154 ≈ 12.47
There is enough for a little more than 12, but not enough for 13 prints.
Shamin Jewelers sells diamond necklaces for $442 less 10%. Jewelers offers the same necklace for $527 less 34%, 14% What additional rate of discount must offer to meet the competitor's price
Answers
Answer:
The selling price of the diamond necklace at Shamin Jewelers after 10% discount is:
$442 * 0.9 = $397.80
The selling price of the same necklace at the competitor's store after 34% and 14% discount is:
$527 * 0.66 * 0.86 = $247.08
So, Shamin Jewelers needs to offer an additional discount to meet the competitor's price:
$397.80 - $247.08 = $150.72
To calculate the additional rate of discount, we divide the difference by the original selling price at Shamin Jewelers and multiply by 100:
($150.72 / $442) * 100 = 34.11%
Therefore, Shamin Jewelers must offer an additional 34.11% discount to meet the competitor's price.
Step-by-step explanation:
(1/5) ³
evaluate
pls help :)
Answers
0.008
1/5 x 1/5 x 1/5
:3
Can someone help me with this please?

Answers
Answer:
The triangles are similar.
Explanation:
Similar triangles have 3 pairs of congruent angles. In this diagram, we can see that the triangles WXP and WYZ share angle W, which is congruent to itself; therefore, they have at least 1 pair of congruent angles. We are given that angle X is congruent to angle Y, so that is a second pair of congruent angles. Finally, we know that angle P is congruent to angle Z because if two pairs of corresponding angles are congruent, then the third pair must also be congruent because the measures of the interior angles of both triangles have to add to 180°.
A real estate agent has 8 master keys to open several new homes. Only 1 master key will open any given house. If 40% of these homes are usually left unlocked, what is the probability that the real estate agent can get into a specific home if the agent selects 3 master keys at random before leaving the office?
Answers
Answer:
Step-by-step explanation:
Suppose F represents the value that a room is unlocked.
Then, we can assume that the probability of unlocked homes is:
P(unlocked homes) = P(U)
P(unlocked homes) = 40%
P(unlocked homes) = 0.40
Also, let us represent the value of the locked room with G.
P(locked homes) = P(G)
P(locked homes) = (1 - 0.40)
P(locked homes) = 0.60
Let the probability of selecting a correct key be P(S)
It implies that for the agent to use 3 keys, we have a combination of \(^8C_3\) possible ways for the set of keys.
Now; since only one will open the house, then:
P(select correct key) = P(S)
\(P(S) = \dfrac{ (^1_1) (^7_2) }{ ^8_3 }\)
\(P(S) = \dfrac{21}{56}\)
P(S) = 0.375
Finally, for the real estate agent to have access to specific homes supposing the agent select three master keys at random prior to the time he left his office, Then:
P(F ∪ (G∩S) = P(F) + P(G∩S)
P(F ∪ (G∩S) = P(F) + P(G) × P(S)
P(F ∪ (G∩S) = 0.40 + (0.60×0.375)
P(F ∪ (G∩S) = 0.40 + 0.225
P(F ∪ (G∩S) =0.625
A geometric sequence has only positive terms. The third term is 100 and the eighth term is 3.125.
Find the common ratio.
Answers
The common ratio of a geometric sequence will be;
⇒ r = 5 / 10
What is Geometric sequence?
An sequence has the ratio of every two successive terms is a constant, is called a Geometric sequence.
Given that;
In a geometric sequence,
The third term is 100 and the eighth term is 3.125.
Now,
We know that;
The nth term of geometric sequence is,
⇒ \(T_{n} = a r^{n - 1}\)
Hence, The third term is;
⇒ \(T_{3} = a r^{3 - 1} = 100\)
⇒ \(a r^{2} = 100\) ..(i)
And, The eighth term is,
⇒ \(T_{8} = a r^{8 - 1} = 3.125\)
⇒ \(a r^{7} = 3.125\) ..(ii)
Divide equation (ii) by (i), we get;
⇒ ar⁷ / ar² = 3.125/100
⇒ r⁷ / r² = 3125 / 100000
⇒ r⁷⁻² = 3125 / 100000
⇒ r⁵ = 3125 / 100000
⇒ r = 5/10
Thus, The common ratio of a geometric sequence will be;
⇒ r = 5 / 10
Learn more about the geometric sequence visit:
https://brainly.com/question/25461416
#SPJ1
Drag and drop each area on top of the triangle it matches. i already did the 4 that have the answers on them qith the teacher. PLS HELP!!

Answers
Answer:
Step-by-step explanation:

A barn contains 11 animals. 7 of the animals are bats and the rest are mice. An animal leaves the barn at random, and then a second animal leaves th at random. Copy and complete the tree diagram, which shows all the possible outcor What is the probability that a mouse leaves first and then a bat? Give your answer as a fraction in its simplest form.
Answers
The probability that a mouse leaves first and then a bat is given as follows:
14/55.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
As the animal is not replaced, the probabilities for this problem are given as follows:
Mice leaves first -> 4/11.Bat leaves second: -> 7/10.Hence the probability is given as follows:
4/11 x 7/10 = 2/11 x 7/5 = 14/55.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION HELP ME WITH THIS QUESTION

Answers
Answer:
B
Step-by-step explanation:
Answer:
B
Step-by-step explanation: look at the graph dude
Planes A and B are shown.
m
n
B
MA
If a new line, p, is drawn parallel to line /, which
statement is true?
O
Line p must be drawn in plane B.
O Line p must be perpendicular to line m.
O Line p must be drawn so that it can lie in the same
plane as line /
O Line p must be drawn in the same plane as line n.
Answers
The line which is on the same plane can be parallel, two lines are never parallel when they are in different planes, so option C is correct.
What is a line?An object having an endless length and no width, depth, or curvature is called a line. Since lines can exist in two, three, or higher-dimensional environments, they are one-dimensional things.
Given:
The given planes are A and B,
A new line, p, is drawn parallel to line l,
Line l in the diagram is located on plane A. Line p must be drawn on plane A in order to be parallel to line l. As a result, line p, which is located on plane B, will be perpendicular to line n and parallel to lines l and n.
To know more about the line:
https://brainly.com/question/2696693
#SPJ1
The image of the remaining question is attached below.

What is the equation of a line
that is perpendicular to the line
y = 2x + 1 and passes through the
point (4, 6)?
А y=-2x+6
B y = 2x + 6
c y=-3x+8
D y = 2x + 8
Answers
Answer:
\(y =-\frac{1}{2}x + 8\)
Step-by-step explanation:
Given
Perpendicular to \(y = 2x + 1\)
Pass through \((4,6)\)
Required
Determine the line equation
First, we need to determine the slope of \(y = 2x + 1\)
An equation is of the form:
\(y = mx + b\)
Where
\(m = slope\)
In this case:
\(m =2\)
Next, we determine the slope of the second line.
Since both lines are perpendicular, the second line has a slope of:
\(m_1 = \frac{-1}{m}\)
\(m_1 = \frac{-1}{2}\)
\(m_1 = -\frac{1}{2}\)
Since this line passes through (4,6); The equation is calculated as thus:
\(y - y_1 = m_1(x - x_1)\)
Where
\((x_1,y_1) = (4,6)\)
This gives:
\(y - 6=-\frac{1}{2}(x - 4)\)
Open bracket
\(y - 6=-\frac{1}{2}x + 2\)
Add 6 to both sides
\(y +6- 6=-\frac{1}{2}x + 2+6\)
\(y =-\frac{1}{2}x + 8\)
What are the domain and range of the relation that models this situation!! Plz help and explain it so Ican understand thank you!

Answers
Answer:
Domain:\(0 \le t \le 9\)
Range: \(7200 \ge \ d \ge \ 0\)
Step-by-step explanation:
Given
\(d = 7200 - 800t\)
Required
Determine the domain and range
From the attached graph, the values of t (on the horizontal axis) starts from 0 and ends at 9.
Hence, the domain is: \(0 \le t \le 9\)
When t = 0:
\(d = 7200 - 800t = 7200 - 800 * 0 = 7200\)
When t = 9
\(d = 7200 - 800t = 7200 - 800 * 9 = 0\)
Hence, the range is:
\(7200 \ge \ d \ge \ 0\)
-5 = -36 / m + m
pls help me with this question hurry
This is 6 grade work
Answers
The solution of the given quadratic equation -5 = -36 / m + m is,
m = - 9 or m = 4
The given equation is
-5 = -36 / m + m
After re arranging it we get,
m² + 5m - 36 = 0
This is nothing but quadratic equation,
Since we know that,
The definition of a quadratic as a second-degree polynomial equation demands that at least one squared term must be included. It also goes by the name quadratic equations. The quadratic equation has the following generic form:
ax² + bx + c = 0
So now we can write,
⇒ m² + 9m - 4m - 36 = 0
⇒ m(m + 9) - 4(m + 9) = 0
⇒ (m + 9)(m - 4) = 0
Therefore,
⇒ (m + 9) = 0 or (m - 4) = 0
⇒ m = - 9 or m = 4
Thus,
The solution of the given expression is
m = - 9 or m = 4
To learn more about quadratic equation visit:
https://brainly.com/question/30098550
#SPJ1
Pls answer 20 points

Answers
Answer:
31.6
Step-by-step explanation:
l^2+w^2=d
30^2+10^2=1,000
square root of 1000 is 31.6
Genevieve has $9000 to invest. She invests some at 6% annual interest and the rest at 4% annual interest. After one year, her total interest from both accounts is $444. How much did she invest in each account? (Clearly label which amount is for which account in your answer. Hint: Over a one year period, annual interest is the same as simple interest.)
Answers
Answer:
The first account, she invested = $4200 and in the second = $4800
Step-by-step explanation:
Let us assume that Genevieve invests $x at 6% ,
Hence, she invests ($9000 - $x ) at 4% ,
It's given that the combined interest from both of the above accounts is $444,
So,
0.06x + 0.04 (9000 - x) = 444
=> 0.06x + 360 - 0.04x = 444
=> (0.06x - 0.04x) + 360 = 444
=> 0.02x = 444 - 360
=> 0.02x = 84
=> x = 84/0.02
=> x = 8400/2 (By multiplying the denominator and numerator)
=> x = 4200
Therefore, 9000 - x = 9000 - 4200 = 4800
$4200 at 6% and $4800 at 4%
Therefore, the first account, she invested = $4200 and in the second = $4800
If my answer helped, kindly mark me as the brainliest!!
Thank You!!
the angle measures of a triangle are 50, 2x, 3x-10. what is the value of x
Answers
Answer:
x = 28°
Step-by-step explanation:
Angle sum property of triangle:
Sum of all the three angles of the triangle is 180°.
50 + 2x + 3x - 10 = 180°
2x + 3x + 50 - 10 = 180°
Combine like terms,
5x + 40 = 180°
Subtract 40 from both sides,
5x = 180 - 40
5x = 140°
Divide both sides by 5,
x = 140 ÷ 5
\(\sf \boxed{\bf x = 28^\circ}\)