48:09
Simone applied the distributive property using the greatest common factor to determine the expression that is equivalent to 24 + 56. Her work is shown below.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
24 + 56 = 8 (4 + 7)
What statement best describes Simone’s error?
Simone did not use the correct factors for 24 in the equation.
Simone did not use the correct factors for 56 in the equation.
Simone did not use the greatest common factor in the equation.
Simone did not use the correct operations in the equation.
Answers
24 + 56
The factors of the numbers are:
24: 1, 2, 3, 4, 6, 8, 12, 24
56: 1, 2, 4, 7, 8, 14, 28, 56
So, factoring we have:
24 + 56 = 8 (3 + 7)
Simone wrote:
24 + 56 = 8 (4 + 7)
Therefore his error is:
Simone did not use the correct factors for 24 in the equation
Answer:
Simone did not use the correct factors for 24 in the equation
Related Questions
Brainlist show all your steps
I will make you brainlist and please label the questions so I can know which answer if for which?
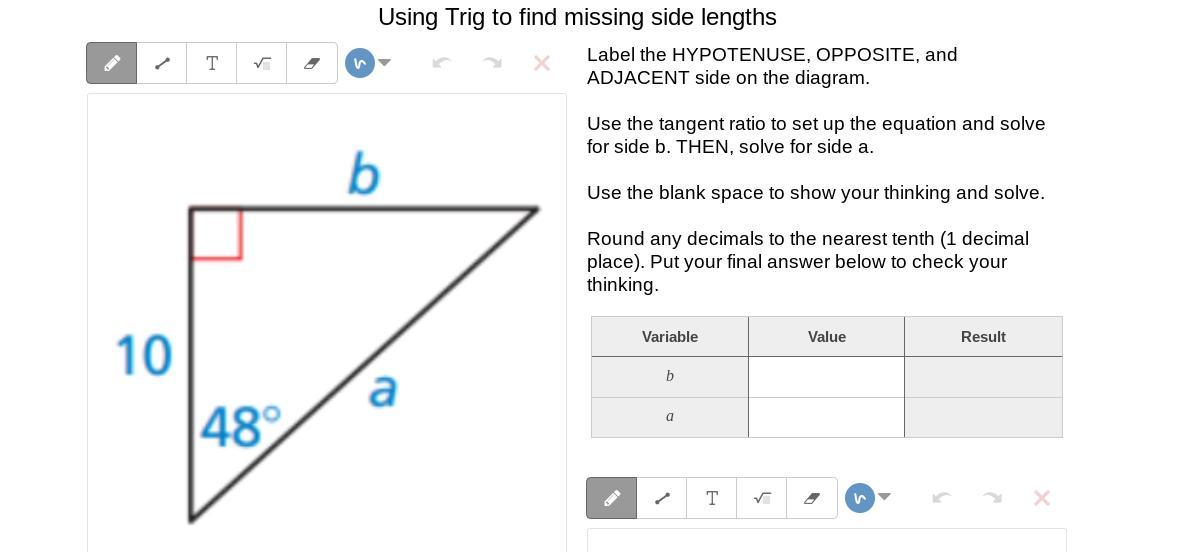

Answers
The values of a and b are:
a = 10sin(132-B)/sin(84)
b = 10sin(96-B)/sin(48)
What is the law of sines?The law of sines, which relates the side lengths of a triangle to the sine of the opposite angles, can be utilized to solve this issue. In particular, for a triangle with sides a, b, and c and inverse points A, B, and C, we have:
a/sin(A) = b/sin(B) = c/sin(C)
let say we have triangle ABC AB=b ,BC = 10 AC =a ,and angle C is 48 degree.
Using this formula, we can find the length of side AC as follows:
a/sin(A) = 10/sin(84) (since angle C is 48 degrees, we know that angle A is 180 - 48 - B = 132 - B degrees)
a = 10*sin(132-B)/sin(84)
To find the length of side AB, we can involve the way that the amount of the points in a triangle is 180 degrees:
A + B + C = 180
B = 180 - A - C = 180 - (132 - B) - 48 = 96 - B
So we know that angle B is 96 - B degrees. Using the law of sines again, we have:
b/sin(B) = 10/sin(48)
b = 10*sin(96-B)/sin(48)
Therefore, the values of a and b are:
a = 10sin(132-B)/sin(84)
b = 10sin(96-B)/sin(48)
know more about trigonometry visit :
https://brainly.com/question/29002217
#SPJ1
5. At a carnival cotton candy and hot dogs are two different prices. Adam buys one cotton candy and one hot dog for $5. Shannon buys 3 cotton candies and one hot dog for $11. How
much is one hot dog? How much is one cotton candy?
Answers
Adam's purchase:
1c + 1h = 5
Shannon's purchase:
3c + 1h = 11
We can now solve this system of equations using substitution or elimination. Here's how to solve using substitution:
From the first equation, we can solve for 1h:
1h = 5 - 1c
We can now substitute this expression for 1h into the second equation:
3c + (5 - 1c) = 11
Simplifying this equation, we get:
2c + 5 = 11
Solving for c, we get:
c = 3
Now that we know the price of one cotton candy is $3, we can substitute this value back into the first equation to solve for h:
1c + 1h = 5
1(3) + 1h = 5
h = 2
Therefore, one hot dog costs $2 and one cotton candy costs $3.
For the pair of functions, write the composite function and its derivative in terms of one input variable. k(t) = 4.5+3 – 7t2 + 3t – 4; t(x) = In x
Answers
The composite function k(t(x)) is -2.5 - 7(ln x)^2 + 3(ln x), and its derivative is -14ln x + 3/x.
To find the composite function k(t(x)), we substitute the expression for t(x) into the function k(t) as follows:
k(t(x)) = 4.5 + 3 - 7t(x)^2 + 3t(x) - 4
k(t(x)) = 4.5 + 3 - 7(ln x)^2 + 3(ln x) - 4
Simplifying this expression, we obtain:
k(t(x)) = -2.5 - 7(ln x)^2 + 3(ln x)
To find the derivative of the composite function, we use the chain rule as follows:
k'(t(x)) = k'(t) * t'(x)
where k'(t) is the derivative of the function k(t) with respect to t, and t'(x) is the derivative of the function t(x) with respect to x.
The derivative of k(t) with respect to t is:
k'(t) = -14t + 3
The derivative of t(x) with respect to x is:
t'(x) = 1/x
Substituting these expressions into the chain rule, we obtain:
k'(t(x)) = (-14t(x) + 3) * (1/x)
k'(t(x)) = (-14ln x + 3/x)
Therefore, the composite function k(t(x)) is -2.5 - 7(ln x)^2 + 3(ln x), and its derivative is -14ln x + 3/x.
To know more about derivative click here
brainly.com/question/29096174
#SPJ11
estion 4: Below are the prices of the same car in different countries.
£1= €1.18 £1 = ¥140
£1 = $1.25
USA
$20000
Ireland
€17500
England
£15000
In which country is the car the best value?
Japan
¥3000000
Answers
From the given question the prices of the same car in different countries best value for the car is in the USA with a price of 16000 euros.
We can use the currency conversion rates to compare the prices of the same car in different countries.
The prices of the same car in different countries are as follows:
USA: $20000
Ireland: €17500
England: £15000
Japan: ¥3000000
To compare these prices, we need to convert them to a common currency.
Here, we can use the conversion rates given in the question:
1 pound = 1.18 euro
1 pound = 140 yen
1 pound = 1.25 dollars
Price of car in euros in Ireland: 17500 euros
Price of car in pounds in England: 15000 pounds = 15000 x 1.18
= 17700 euros
Price of car in dollars in USA: 20000 dollars
= 20000 / 1.25 = 16000 euros
Price of car in yen in Japan: 3000000 yen = 3000000 / 140
= 21428.57 euros
Best value for the car is in the USA with a price of 16000 euros.
For more related questions on best value:
https://brainly.com/question/31938563
#SPJ8
In space, how many planes can be perpendicular to a given line at a given point on that line in space?
A. 1
B.0
C. 3
D. infinitely many
Answers
In space, there can be infinitely many planes that are perpendicular to a given line at a given point on that line.
The correct answer is Option D.
The key concept here is that a plane is defined by having at least three non-collinear points.
When a line is given, we can choose any two points on that line, and then construct a plane that contains both the line and those two points. By doing so, we ensure that the plane is perpendicular to the given line at the chosen point.
Since we can select an infinite number of points on the given line, we can construct an infinite number of planes that are perpendicular to the line at various points.
Thus, the correct answer is D. infinitely many planes can be perpendicular to a given line at a given point in space.
The correct answer is Option D.
For more such questions on perpendicular
https://brainly.com/question/1202004
#SPJ8
A rectangular sheet of paper has a perimeter of 60cm. When it is folded in half along its longer line of symmetry, the perimeter of the rectangle which this creates is 49cm. What are the dimensions of the original shape?
Answers
Answer:
Dimensions of the original rectangle:
Length = 19 cm
Width = 11 cm
Step-by-step explanation:
Let
Length = x
Width = y
Original rectangle:
2(Length + width) = 60
2x + 2y = 60
New rectangle has same length with original rectangle but half of the width of the original rectangle when folded
Length = x
Width = 1/2y
2(Length + 1/2width) = 49
2x + y = 49
2x + 2y = 60 (1)
2x + y = 49 (2)
Subtract (2) from (1) to eliminate x
2y - y = 60 - 49
y = 11
Substitute y = 11 into (2)
2x + y = 49
2x + 11 = 49
2x = 49 - 11
2x = 38
x = 38/2
x = 19
Dimensions of the original rectangle:
Length = 19 cm
Width = 11 cm
Ms.Groves has trays of paint for her students in her art class.Each tray has 5 colors.One of the colors is purple.What fraction of the colors in 20 trays is purple?
Answers
Two circles are concentric circles if and only if they have, congruent radii.
Answers
Two circles are concentric circles if and only if they have congruent radii.
When we say that two circles are concentric, it means that they share the same center point. In other words, the centers of the two circles coincide. The main characteristic that makes two circles concentric is that they have the same radius.
The radius of a circle is the distance from the center to any point on the circumference. When two circles have the same radius, it means that the distance from their centers to any point on their circumferences is equal. This makes the circles identical in size and shape.
Conversely, if two circles have congruent radii, it implies that their centers coincide, making them concentric circles. The congruence of the radii ensures that the distance from the center to any point on the circumference is the same for both circles.
Learn more about concentric circles here:
brainly.com/question/30451430
#SPJ11
the list shows the weight in pounds of 6 puppies at birth. 3, 1.6, 2.8, 2.5, 1.7, 2.8 what is the mean absolute deviation of these numbers?
Answers
Step 1: Find the mean (average) of the numbers.
Mean = (3 + 1.6 + 2.8 + 2.5 + 1.7 + 2.8) / 6 = 2.3667 (rounded to 4 decimal places)
Step 2: Find the absolute deviation of each number by subtracting the mean from each number and taking the absolute value.
|3 - 2.3667| = 0.6333
|1.6 - 2.3667| = 0.7667
|2.8 - 2.3667| = 0.4333
|2.5 - 2.3667| = 0.1333
|1.7 - 2.3667| = 0.6667
|2.8 - 2.3667| = 0.4333
Step 3: Find the mean of the absolute deviations.
MAD = (0.6333 + 0.7667 + 0.4333 + 0.1333 + 0.6667 + 0.4333) / 6
MAD = 0.5 (rounded to 1 decimal place)
Therefore, the mean absolute deviation of the given set of numbers is 0.5.
sacha had $60.00 she spent 1 /4 on food and saved the rest how much did she save ?
Answers
Answer:
45
Step-by-step explanation:
1/4 of a number means the number divided by 4. 60/4=15. That's how much she spent, and we have to find the rest. So we do 60-15=45.
1/4 = 15
We know that sacha saved 3/4 so we multiply 3 by 15 which is 45.
This means sacha saves $45. Hope this helps!
convert the Roman Numeral CCCXL (with two lines above it) to Hindu-Arabic form
Answers
Each line above the numbers multiply it by 1000. So this number is being multiplied by 1000000.
Each "C" is equal to 100, since there are "CCC" the number is 300.
"XL" is equal to 40, because "X" is equal to 10 and "L" is equal to 50, but since he X is on the left of the L we subtract them.
The number CCCXL is then 340, but there are the two lines. So we have:
\(\bar{\bar{CCCXL}}=340\cdot1000\cdot1000=340,000,000\)a diver was collecting water samples from a lake. he collected a sample at every 3m, starting at 5m below water surface. the final sample was collected at a depth of 35m.how many sample did he collected
Answers
The diver collected water samples at every 3 meters, starting from 5 meters below the water surface, up to a final depth of 35 meters.
We can find the number of samples collected by dividing the total depth range by the distance between each sample and then adding 1 to include the first sample.
The total depth range is:
35 m - 5 m = 30 m
The distance between each sample is 3 m, so the number of samples is:
(30 m) / (3 m/sample) + 1 = 10 + 1 = 11
Therefore, the diver collected a total of 11 water samples.
The perimeter of a rectangular swimming pool is 42m. The length is 5 meters more than the width. What is the length of the swimming pool?
Answers
Answer:
Length is 13 meters
Step-by-step explanation:
Length: x + 5
Width: x
2L + 2W = Perimeter
2(x+5) + 2x = 42
2x + 10 + 2x = 42
4x + 10 = 42
4x = 32
x = 8
Length: 8 + 5 = 13
Width: 8
store dedicated to removing stains from expensive suits claims that a new product
Stain remover will remove more than 70% of the stains it is applied to. To verify
this statement the stain remover product will be used on 12 stains chosen at
random. If fewer than 11 of the spots are removed, the null hypothesis that p =
0.7; otherwise, we will conclude that p > 0.7. (tables are not allowed in this problem)
a) Evaluate the probability of making a type I error, assuming that p = 0.7.
b) Evaluate the probability of committing a type II error, for the alternative p = 0.9.
Please answer step by step and include the formulas use
Answers
a) The probability of making a type I error, assuming p = 0.7, is 0.2515, or 25.15%.
b) The probability of committing a type II error, assuming p = 0.9, is 0.4029, or 40.29%.
a) Probability of Type I Error (assuming p = 0.7):
A type I error occurs when we reject the null hypothesis (p = 0.7) when it is actually true.
In this case, we reject the null hypothesis if fewer than 11 stains are removed out of 12.
Using the binomial distribution formula,
We have fewer than 11 successes (stains removed) out of 12 attempts, assuming the null hypothesis is true (p = 0.7).
So, P(X < 11) = Σ (nCr) x \(p^r (1-p)^{(n-r)\), where X follows a binomial distribution.
P(X < 11) = P(X = 0) + P(X = 1) + ... + P(X = 10)
P(X < 11) ≈ 0.2515
Therefore, the probability of making a type I error, assuming p = 0.7, is 0.2515, or 25.15%.
b) A type II error occurs when we fail to reject the null hypothesis (p = 0.7) when the alternative hypothesis (p > 0.7) is true.
In this case, we fail to reject the null hypothesis if 11 or more stains are removed out of 12.
Similarly, using the binomial distribution formula,
P(X ≥ 11) = P(X = 11) + P(X = 12)
P(X = 11) = (12C11) x 0.9¹¹ x (1-0.9)⁽¹²⁻¹¹⁾
P(X = 12) = (12C12) x 0.9¹² x (1-0.9)⁽¹²⁻¹²⁾
Calculating these probabilities:
P(X ≥ 11) = P(X = 11) + P(X = 12)
= (12C11) x 0.9¹¹ x (1-0.9)⁽¹²⁻¹¹⁾+ (12C12) x 0.9¹² x (1-0.9)⁽¹²⁻¹²⁾
≈ 0.4029
Therefore, the probability of committing a type II error, assuming p = 0.9, is 0.4029, or 40.29%.
Learn more about Probability here:
https://brainly.com/question/23637205
#SPJ4
Assume that p is a relation that contains the points (3, -4). What other point must be included in the relation if p is:1. symmetric about the x-axis?2. symmetric about the y-axis?
Answers
The point needed for the relation is \(P(x,y) = (3, 4)\) if P and P' are symmetric about the x-axis.
The point needed for the relation is \(P(x,y) = (-3, -4)\) if P and P' are symmetric about the y-axis.
In this exercise we are supposed to determine the coordinates of a point P under an assumption of rigid transformation. Now, we must use the following symmetry transformations:
Reflection about the x-axis
\(S'(x,y) = S(x,y) - 2\cdot (0, s_{y})\) (1)
Reflection about the y-axis
\(S'(x,y) = S(x,y) - 2\cdot (s_{x}, 0)\) (2)
Where:
\(S(x,y)\) - Original point.\(S' (x,y)\) - Reflected point. \(s_{x}, s_{y}\) - Coordinates of point S.If we know that \(P'(x,y) = (3, -4)\), the coordinates for each reflection are, respectively:
Reflection about the x-axis
\(P(x,y) = (3,-4) - 2\cdot (0, -4)\)
\(P(x,y) = (3, 4)\)
\(P(x,y) = (3, 4)\) if P and P' are symmetric about the x-axis.
Reflection about the y-axis
\(P(x,y) = (3, -4) - 2\cdot (3, 0)\)
\(P(x,y) = (-3, -4)\)
\(P(x,y) = (-3, -4)\) if P and P' are symmetric about the y-axis.
We kindly invite to see this question on rigid transformations: https://brainly.com/question/18613109
I need help!!! Can you put this in order for me !

Answers
7=2x+4
3=2x
X=3/2
whats the answer to number 5 please and thank you? please write down the steps
please help

Answers
Answer:
67
Step-by-step explanation:
Answer:
35
Step-by-step explanation:
x + 55 = 90 (Right angle triangle)
x = 90 - 55
x = 35
Please mark as brainliest.
The graph of the function f ( x ) is shown

Answers
The true statements for the given function f(x) are:
The value of g(1) is 3 and the y- intercept of g(x) is at the point (0, 1) .
How to calculate the values of the function?The function g(x) = f( x - 3 )
g (1) = f (1 -3 )
= f (-2 )
= 3
g (-1) = f (-1 -3)
= f (-4)
= - 1
Substituting , x = 0 to find the y intercept of g(x)
g ( 0 ) = f ( 0 - 3)
=f (-3)
=1
The y intercept of g(x) is at the point (0, 1)
Thus, options 1 and 4 are the true statements for the given function.
What are functions?Function is a mathematical phrase, rule, or law that establishes the relationship between an independent variable and a dependent variable.In science, engineering, and the majority of the mathematical disciplines, functions are often utilized.Functions are reportedly the central objects of inquiry in the majority of mathematical disciplines. Although some authors establish a distinction between maps and functions, functions are also referred to as maps or mappings.To learn more about functions, refer:
https://brainly.com/question/25638609
#SPJ1
if discrete-time system has sampling period of t 0.2 s, has a rise time of 1 $, and an overshoot of 0.2; give a homogeneous difference equation of the form ik for this system.
Answers
The homogeneous difference equation for this system is: y[k] = 0.379*y[k-1] - 0.145*y[k-2]
The homogeneous difference equation for a discrete-time system with a sampling period of t=0.2s, a rise time of 1s, and an overshoot of 0.2 can be given as follows:
y[k] = a*y[k-1] + b*y[k-2]
Where y[k] is the output at time k, y[k-1] is the output at time k-1, and y[k-2] is the output at time k-2. The coefficients a and b are determined by the system's sampling period, rise time, and overshoot.
To find the coefficients a and b, we can use the following equations:
a = (2*exp(-t/tau))/(1+exp(-2*t/tau))
b = -(exp(-2*t/tau))/(1+exp(-2*t/tau))
Where tau is the time constant of the system, t is the sampling period, and exp is the exponential function. For this system, t=0.2s and tau=1s/ln(1+0.2)=0.223s. Plugging these values into the equations for a and b gives:
a = (2*exp(-0.2/0.223))/(1+exp(-2*0.2/0.223)) = 0.379
b = -(exp(-2*0.2/0.223))/(1+exp(-2*0.2/0.223)) = -0.145
Therefore, the homogeneous difference equation for this system is:
y[k] = 0.379*y[k-1] - 0.145*y[k-2]
Learn more about the homogeneous difference: https://brainly.com/question/2396847
#SPJ11
what is the projection of (4 4) onto (3 1)
Answers
The projection of the point (4,4) onto the line passing through (3,1) is the point on the line that is closest to (4,4). To find this projection, we need to first find the direction vector of the line, which is (3-1, 1-0) = (2,1).
Next, we need to find the vector from the point (3,1) to the point (4,4), which is (4-3, 4-1) = (1,3).
Then, we can use the formula for projecting a vector onto another vector:
proj_v u = ((u · v) / (v · v)) v
where u is the vector we want to project, v is the vector we want to project onto, and · denotes the dot product.
Applying this formula, we get:
proj_v u = ((1,3) · (2,1)) / ((2,1) · (2,1)) (2,1)
= (5/5) (2,1)
= (2,1)
So the projection of (4,4) onto the line passing through (3,1) is the point (3,1) + (2,1) = (5,2).
To find the projection of vector (4, 4) onto vector (3, 1), you can follow these steps:
Step 1: Calculate the dot product of the two vectors.
Dot product = (4 * 3) + (4 * 1) = 12 + 4 = 16
Step 2: Calculate the magnitude squared of the vector you are projecting onto (3, 1).
Magnitude squared = (3 * 3) + (1 * 1) = 9 + 1 = 10
Step 3: Divide the dot product by the magnitude squared.
Scalar = 16 / 10 = 1.6
Step 4: Multiply the scalar by the vector you are projecting onto (3, 1) to find the projection.
Projection = 1.6 * (3, 1) = (4.8, 1.6)
So, the projection of (4, 4) onto (3, 1) is (4.8, 1.6).
learn nine about projection here:brainly.in/question/2210182
#SPJ11
Solve for x. Round to the nearest tenth, if necessary.

Answers
Answer:
35
Step-by-step explanation:
Find the area of the blue region.
10 m
5.5 m
4m
A. 40 m²
B. 26.5 m²
C. 48 m²
D. 70 m²
7m

Answers
Answer:
the answer is 48m²
Step-by-step explanation:
mark me brainlist please!!

57 toys are split into groups of 4 toys. What question do we need to answer here? pls answer quick! this test is already missing and I need to complete it! please no wrong answers :(( it's due in like 20 mins :/
Answers
Answer:
how many toys are in each group?
x^(1/12) = 49^(1/24), find x
Answers
The calculated value of x in the expression x^(1/12) = 49^(1/24) is 7
Calculating the value of x in the expressionFrom the question, we have the following parameters that can be used in our computation:
x^(1/12) = 49^(1/24)
Express 49 as 7^2
So, we have
x^(1/12) = 7^(2 * 1/24)
Evaluate the products
This gives
x^(1/12) = 7^(1/12)
When both sides of the equations are compared, we have
x = 7
Hence, the value of x in the expression is 7
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
solve for x. 150 degrees and 5x

Answers
Answer:
6
Step-by-step explanation:
150+5x=180(linear pair)
30=5x
x=6
find the surface area of this cylinder to 1dp
h=18cm
r=12cm
please help
thanks
Answers
The surface area of the cylinder is 2262.9 \(cm^{2}\)
What is a Cylinder?Cylinder is a three-dimensional solid shape that consists of two identical and parallel bases linked by a curved surface. it is made up of a circled surface with a circular top and a circular base.
To find the surface area of a cylinder,
Surface area = 2πr (r + h)
Where π = 22/7
r = 12 cm
h = 18 cm
So, the surface area = 2 * 22/7 * 12 (12 + 18)
SA = 44/7 * 12(12 + 18)
SA = 44/7 * 12(30)
SA = 44/7 * 360
SA = 15840/7
SA = 2262.9 \(cm^{2}\)
Therefore, the surface area of cylinder 2262.9 \(cm^{2}\)
Read more about Cylinder
https://brainly.com/question/21405772
#SPJ1
find the mean of the following 205,208,205,200,210,300,210,180.
Answers
by adding all of the numbers together and dividing it by the amount of numbers you have (8), you got 214.75
Please help me asap ill give
Brainlyest

Answers
Answer:
TS = 6.6 (nearest tenth)
Step-by-step explanation:
Secant: a straight line that intersects a circle at two points.
Tangent: a straight line that touches a circle at only one point.
Theorem
When a secant segment and a tangent segment meet at an exterior point, the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
Given:
Tangent segment = QRSecant segment = TRExternal secant segment = SR⇒ QR² = TR · SR
⇒ 19² = (TS + 16) · 16
⇒ 361 = (TS + 16) · 16
⇒ 22.5625 = TS + 16
⇒ TS = 22.5625 - 16
⇒ TS = 6.5625
⇒ TS = 6.6 (nearest tenth)
Suppose (-5,1) is a point on a graph of y=f(x). What is a point that will be on the graph of y =f (-7x) -4
Answers
f(-5) = 1
f((-7)(5/7)) = f(-5) = 1
When x = 5/7: f(-7(5/7)) - 4 = 1 - 4 = -3
(5/7, -3) is a point on the graph of y = f(-7x) -4
Determine the equation for each polynomial function.
a) A cubic function with zeros -3 (multiplicity 2) and 2, and y-intercept -36
b) A quartic (fourth degree) function with a negative leading coefficient, zeros -2 (multiplicity 2) and 3 (multiplicity 2), and a constant term of -6.
Answers
The solutions for the given polynomial function are:
a) The equation for the cubic function is: f(x) = 2(x + 3)(x + 3)(x - 2)
b) The equation for the quartic function is: f(x) = -1/6(x + 2)(x + 2)(x - 3)(x - 3)
a) To determine the equation for the cubic function with zeros -3 (multiplicity 2) and 2 and a y-intercept of -36, we can use the factored form of a cubic function:
\(f(x) = a(x - r_1)(x - r_2)(x - r_3)\)
where \(r_1\), \(r_2\) and \(r_3\) are the function's zeros, and "a" is a constant that scales the function vertically.
In this case, the zeros are -3 (multiplicity 2) and 2. Thus, we have:
f(x) = a(x + 3)(x + 3)(x - 2)
To determine the value of "a," we can use the y-intercept (-36). Substituting x = 0 and y = -36 into the equation, we have:
-36 = a(0 + 3)(0 + 3)(0 - 2)
-36 = a(3)(3)(-2)
-36 = -18a
Solving for "a," we get:
a = (-36) / (-18) = 2
Therefore, the equation for the cubic function is:
f(x) = 2(x + 3)(x + 3)(x - 2)
b) To determine the equation for the quartic function with a negative leading coefficient, zeros -2 (multiplicity 2) and 3 (multiplicity 2), and a constant term of -6, we can use the factored form of a quartic function:
\(f(x) = a(x - r_1)(x - r_1)(x - r_2)(x - r_2)\)
where \(r_1\) and \(r_2\) are the zeros of the function, and "a" is a constant that scales the function vertically.
In this case, the zeros are -2 (multiplicity 2) and 3 (multiplicity 2). Thus, we have:
f(x) = a(x + 2)(x + 2)(x - 3)(x - 3)
To determine the value of "a," we can use the constant term (-6). Substituting x = 0 and y = -6 into the equation, we have:
-6 = a(0 + 2)(0 + 2)(0 - 3)(0 - 3)
-6 = a(2)(2)(-3)(-3)
-6 = 36a
Solving for "a," we get:
a = (-6) / 36 = -1/6
Therefore, the equation for the quartic function is:
f(x) = -1/6(x + 2)(x + 2)(x - 3)(x - 3)
Learn more about Polynomial functions at:
https://brainly.com/question/31528136
#SPJ4