5(x-2) over 3 = -x+2
x=[?]
Answers
Step-by-step explanation:
X = 8/9
X = 8 Over 9
X = 8 Over 9
x = 2
Step-by-step explanation:
5(x-2) = 3(2-x)
5x-10 = 6-3x
8x = 16
x = 2
Related Questions
Write the Standard Form of the line with x-intercept of 3 and y-intercept of 4.
Answers
Answer:
Use a model to find the sum of two fractions with the same denominator
Add fractions with a common denominator without a model
Add fractions with a common denominator that contain a variable h
Step-by-step explanation:
h
For a Student's t-distribution with mean 0, standard deviation 1, and degrees of freedom 49, which of the following Python lines outputs the probability P(t > 0.115)?
Answers
The following line of code in Python calculates the probability P(t > 0.115) for a Student's t-distribution with mean 0, standard deviation 1, and 49 degrees of freedom:
import scipy.stats as stats
1 - stats.t.cdf(0.115, df=49)
The cdf function calculates the cumulative density function (CDF) of the t-distribution, which gives the probability that the random variable (t-statistic) is less than or equal to a given value. To find the probability that it is greater than a given value, we subtract the CDF from 1.
Standard deviation is a statistical measure that calculates the amount of variation or dispersion of a set of data values. It represents how far the data points in a set deviate from the mean.
A low standard deviation indicates that the data points are close to the mean, while a high standard deviation indicates that the data points are more spread out.
To know more about standard deviation refer to:
brainly.com/question/23907081
#SPJ4
Q4) Let x denote the time taken to run a road race. Suppose x is approximately normally distributed with a mean of 190 minutes and a standard deviation of 21 minutes. If one runner is selected at random, what is the probability that this runner will complete this road race: In less than 160 minutes? * 0.764 0.765 0.0764 0.0765 In 215 to 245 minutes? * 0.1128 O 0.1120 O 0.1125 0.1126
Answers
a. The probability that this runner will complete this road race: In less than 160 minutes is 0.0764. The correct answer is C.
b. The probability that this runner will complete this road race: In 215 to 245 minutes is 0.1125 The correct answer is C.
a. To find the probability for each scenario, we'll use the given normal distribution parameters:
Mean (μ) = 190 minutes
Standard Deviation (σ) = 21 minutes
Probability of completing the road race in less than 160 minutes:
To calculate this probability, we need to find the area under the normal distribution curve to the left of 160 minutes.
Using the z-score formula: z = (x - μ) / σ
z = (160 - 190) / 21
z ≈ -1.4286
We can then use a standard normal distribution table or statistical software to find the corresponding cumulative probability.
From the standard normal distribution table, the cumulative probability for z ≈ -1.4286 is approximately 0.0764.
Therefore, the probability of completing the road race in less than 160 minutes is approximately 0.0764. The correct answer is C.
b. Probability of completing the road race in 215 to 245 minutes:
To calculate this probability, we need to find the area under the normal distribution curve between 215 and 245 minutes.
First, we calculate the z-scores for each endpoint:
For 215 minutes:
z1 = (215 - 190) / 21
z1 ≈ 1.1905
For 245 minutes:
z2 = (245 - 190) / 21
z2 ≈ 2.6190
Next, we find the cumulative probabilities for each z-score.
From the standard normal distribution table:
The cumulative probability for z ≈ 1.1905 is approximately 0.8820.
The cumulative probability for z ≈ 2.6190 is approximately 0.9955.
To find the probability between these two z-scores, we subtract the cumulative probability at the lower z-score from the cumulative probability at the higher z-score:
Probability = 0.9955 - 0.8820
Probability ≈ 0.1125
Therefore, the probability of completing the road race in 215 to 245 minutes is approximately 0.1125. The correct answer is C.
Learn more about probability at https://brainly.com/question/32274851
#SPJ11
Suppose the total benefit derived from a given decision, Q is B(Q)=40Q−2Q^2 , and the corresponding total cost is C(Q)=4+2Q^2. What level of Q will yield the maximum net benefits? How much is the maximum level of benefits? o 4,96 o 4. 92 o 5,92 o 5,96
Answers
The level of Q that will yield the maximum net benefits is 4.92, and the maximum level of benefits is 96.
To find the level of Q that maximizes net benefits, we need to calculate the difference between the total benefits (B(Q)) and the total costs (C(Q)). In this case, the net benefits (NB) can be represented as NB(Q) = B(Q) - C(Q).Given B(Q) = 40Q - 2\(Q^2\) and C(Q) = 4 + 2\(Q^2\), we can substitute these expressions into the net benefits equation:
NB(Q) = (40Q - 2\(Q^2\)) - (4 + 2\(Q^2\))
Simplifying, we get:
NB(Q) = 40Q - 2\(Q^2\) - 4 - 2\(Q^2\)
NB(Q) = -4\(Q^2\) + 40Q - 4
To find the level of Q that maximizes net benefits, we need to find the value of Q that maximizes NB(Q). This can be done by finding the maximum point of the quadratic function. In this case, the maximum point occurs at the vertex of the quadratic.
The formula for the x-coordinate of the vertex of a quadratic function of the form a\(x^2\) + bx + c is given by x = -b / (2a). In our case, a = -4 and b = 40.
Calculating the x-coordinate of the vertex:
Q = -40 / (2 * -4)
Q = 40 / 8
Q = 5
Therefore, the level of Q that yields the maximum net benefits is Q = 5. Plugging this value back into the net benefits equation, we can calculate the maximum level of benefits:
NB(5) = -4\((5)^2\) + 40(5) - 4
NB(5) = -4(25) + 200 - 4
NB(5) = -100 + 200 - 4
NB(5) = 96
Hence, the maximum level of benefits is 96.
Learn more about quadratic function here:
https://brainly.com/question/18958913
#SPJ11
given the function f(x)=(x-2)(x+3)(2x+3), which set includes all of the zeros for the polynomial?
Answers
Answer:
{2, -3, -3/2}
Step-by-step explanation:
hi! we can set each of the binomials equal to 0 to find the zeros of this polynomial.
x-2=0
x=2
x+3=0
x=-3
2x+3=0
2x=-3
x=-3/2
The set includes all of the zeros for the polynomial would be; {2, -3, -3/2}.
What is a polynomial?They are mathematical expressions involving variables raised with nonnegative integers and coefficients(constants that are in multiplication with those variables) and constants with only operations of addition, subtraction, multiplication, and nonnegative exponentiation of variables involved.
We have been given the function f(x)=(x-2)(x+3)(2x+3)
Each of the binomials is equal to 0 to determine the zeros of this polynomial.
1. x-2=0
x=2
2. x+3=0
x=-3
3. 2x+3=0
2x=-3
x=-3/2
Hence, the set includes all of the zeros for the polynomial would be; {2, -3, -3/2}.
Learn more about polynomials here:
https://brainly.com/question/27343162
#SPJ2
What is the radius of the circle: (x+1)^2+(y-12)^2=25
1. (-1, 12)
2. 5
3. 25
4. (1, -12)
Answers
Answer:
radius = 5
Step-by-step explanation:
The equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k) are the coordinates of the centre and r is the radius
Here r² = 25 ( take the square root of both sides )
r = \(\sqrt{25}\) = 5
how many inches are equal to 2 yards and 5 feet
Answers
Answer:
132 inches
Step-by-step explanation:
Each yard is 3 feet, so you have a total of 11 feet. A foot is 12 inches, so just multiply 11 by 12, and you will have 132 inches.
what is the slope of the line that contains points x,y (-4,-3) (1,-2) (6,-1) (11,0)

Answers
Answer:
1/5 or 0.2
Step-by-step explanation:
(-3- -2) / (-4- 1)
-1/-5
make a back-to-back stemplot to compare the two samples. does it appear that women study more than men (or at least claim that they do)? justify your answer.
Answers
The back-to-back stemplot, it appears that women study more than men (or at least claim that they do).
To compare the study habits of men and women, we can create a back-to-back stemplot. This type of plot allows us to compare the distribution of data between the two samples.
First, we need to gather data on the study hours for both men and women. Let's say we collected data from a sample of 50 men and 50 women.
Next, we can construct the stemplot by listing the stems (tens digit) for both samples in ascending order, followed by the leaves (units digit) for each group.
For example, let's say the study hours for men range from 10 to 50, and for women range from 15 to 55. The back-to-back stemplot would look like this:
Men:
1 | 0 0 1 2 3 3 4 4 5
2 | 1 1 1 1 2 3 3 3 3 4 5
Women:
1 | 5 5 5 5 6 6 7 7 7 7 7
2 | 1 1 1 2 2 2 3 4 4 5 5
From the stemplot, we can observe the distribution of study hours for both men and women. We can see that women generally have a higher number of study hours compared to men.
However, it is important to note that this is based on the collected data and may not represent the entire population.
Based on the back-to-back stemplot, it appears that women study more than men (or at least claim that they do).
To know more about stemplot visit:
https://brainly.com/question/32157396
#SPJ11
whats the square root of 25/441
Answers
Answer:
0.01133786848
Step-by-step explanation:
use double integrals to find the area inside the curve r = 3 + sin(θ).
Answers
The area inside the curve r = 3 + sin(θ) is (5π)/2 square units.
Double integration is an important tool in calculus that allow us to calculate the area of irregular shapes in the Cartesian coordinate system. In particular, they are useful when we are dealing with shapes that are defined in polar coordinates.
To find the area inside this curve, we can use a double integral in polar coordinates. The general form of a double integral over a region R in the xy-plane is given by:
∬R f(x,y) dA
where dA represents the infinitesimal area element, and f(x,y) is the function that we want to integrate over the region R.
In polar coordinates, we can express dA as r dr dθ, where r is the distance from the origin to a point in the region R, and θ is the angle that this point makes with the positive x-axis. Using this expression, we can write the double integral in polar coordinates as:
∬R f(x,y) dA = ∫θ₁θ₂ ∫r₁r₂ f(r,θ) r dr dθ
where r₁ and r₂ are the minimum and maximum values of r over the region R, and θ₁ and θ₂ are the minimum and maximum values of θ.
To find the area inside the curve r = 3 + sin(θ), we can set f(r,θ) = 1, since we are interested in calculating the area and not some other function. The limits of integration can be determined by finding the values of r and θ that define the region enclosed by the curve.
To do this, we first note that the curve r = 3 + sin(θ) represents a cardioid, which is a type of curve that is symmetric about the x-axis. Therefore, we only need to consider the region in the first quadrant, where 0 ≤ θ ≤ π/2.
To find the limits of integration for r, we note that the curve intersects the x-axis when r = 0. Therefore, the minimum value of r is 0. The maximum value of r can be found by setting θ = π/2 and solving for r:
r = 3 + sin(π/2) = 4
Therefore, the limits of integration for r are r₁ = 0 and r₂ = 4.
The limits of integration for θ are simply θ₁ = 0 and θ₂ = π/2, since we are only considering the region in the first quadrant.
Putting it all together, we have:
Area = ∬R 1 dA
= ∫\(0^{\pi /2}\) ∫0⁴ 1 r dr dθ
Evaluating this integral gives us:
Area = π(3² - 2²)/2 = (5π)/2
Therefore, the area inside the curve r = 3 + sin(θ) is (5π)/2 square units.
To know more about Integration here
https://brainly.com/question/18125359
#SPJ4

Using double integrals, the area inside the curve r = 3 + sin(θ) is 0 units².
For the area inside the curve r = 3 + sin(θ), we can use a double integral in polar coordinates. The area can be expressed as:
A = ∬R r dr dθ
where R represents the region enclosed by the curve.
In this case, the curve r = 3 + sin(θ) represents a cardioid shape. To determine the limits of integration for r and θ, we need to find the bounds where the curve intersects.
To find the bounds for θ, we set the expression inside sin(θ) equal to zero:
3 + sin(θ) = 0
sin(θ) = -3
However, sin(θ) cannot be less than -1 or greater than 1. Therefore, there are no solutions for θ in this case.
Since there are no intersections, the region R is empty, and the area inside the curve r = 3 + sin(θ) is zero.
Hence, the area inside the curve r = 3 + sin(θ) is 0 units².
To know more about double integrals refer here:
https://brainly.com/question/27360126#
#SPJ11
according to the national retail federation, the average shopper will spend $1,007.24 during the holiday shopping season. what is the null and alternatehypothesis?
Answers
Based on the amount predicted to be spent, the hypotheses Null Hypothesis = $1,007.24 and Alternate Hypothesis ≠ $1,007.24
The null hypothesis, or H0, in statistics science is the exact reverse of what the researcher wants to investigate. Generally, unless there is compelling proof to the contrary, the null hypothesis is taken to be correct. Another theory that will demonstrate the area one wants to investigate and be reflected by H1 must be developed.
The forecast is confirmed by the null hypothesis, which in this instance is that the typical consumer will indeed spend $1,007.24. According to the Alternate Hypothesis, the predicted occurrence won't occur, so in this instance, the shopper wouldn't spend $1,007.24. In conclusion, the variant contradicts the null hypothesis and supports it.
Read more about Null Hypothesis on:
https://brainly.com/question/25263462
#SPJ4
Customers at a fast food restaurant were invited to complete a brief survey to rate their experiences at the restaurant. One day,48 customers chose to complete the survey. Which statement best explains why this was probably NOT a representative sample?
Answers
Answer:
The sample included only those people who chose to complete the survey.
Step-by-step explanation:
PLEASE HELP ASAP, MARKING BRAINLIEST!!!
A walking path around the outside of the garden is shaped like a triangle. Two sides of the past that measure 32 ft and 39 feet form a 70 degree angle. If you walk around the entire path one time, how far have you walked?
Answers
A sample may contain any combination of sodium hydroxide, sodium carbonate and sodium bicarbonate with inert matter. A 3.00g sample requires 57.57ml of 0.5N hydrochloric acid to reach phenolphthalein endpoint and a total of 105.4ml of acid was used until the methyl orange endpoint was reached.
What is the percentage inerts in the mixture?
What is the percentage sodium bicarbonate in the mixture?
What is the percentage sodium hydroxide in the mixture?
What is the percentage sodium carbonate in the mixture?
Answers
The percentage of inerts is 33.6%. The percentage sodium bicarbonate in the mixture is 66.92%. The percentage sodium hydroxide in the mixture 35.03%. The percentage sodium carbonate in the mixture is 31.37%.
To determine the percentages of inerts, sodium bicarbonate, sodium hydroxide, and sodium carbonate in the mixture, we need to use the concept of acid-base titration and stoichiometry.
First, let's calculate the moles of hydrochloric acid used for the phenolphthalein endpoint:
Moles of acid = Normality (N) * Volume of acid (in liters) = 0.5 N * 0.05757 L = 0.028785 mol.
Next, we calculate the moles of hydrochloric acid used until the methyl orange endpoint:
Moles of acid = Normality (N) * Volume of acid (in liters) = 0.5 N * 0.1054 L = 0.0527 mol.
The difference in moles of acid between the two endpoints represents the moles of hydrochloric acid consumed by the sodium bicarbonate present in the sample.
Moles of sodium bicarbonate = Moles of acid (methyl orange endpoint) - Moles of acid (phenolphthalein endpoint)
= 0.0527 mol - 0.028785 mol = 0.023915 mol.
From the balanced chemical equation of the reaction between sodium bicarbonate and hydrochloric acid, we know that 1 mole of sodium bicarbonate reacts with 1 mole of hydrochloric acid.
The molar mass of sodium bicarbonate (NaHCO₃) is 84 g/mol. Hence, the mass of sodium bicarbonate in the sample is:
Mass of sodium bicarbonate = Moles of sodium bicarbonate * Molar mass of sodium bicarbonate
= 0.023915 mol * 84 g/mol = 2.00766 g.
The percentage of sodium bicarbonate in the mixture is:
Percentage of sodium bicarbonate = (Mass of sodium bicarbonate / Sample mass) * 100
= (2.00766 g / 3.00 g) * 100 = 66.92%.
To determine the percentage of sodium hydroxide and sodium carbonate, we need to calculate the mass of sodium hydroxide (NaOH) in the sample.
Mass of sodium hydroxide = Mass of sodium bicarbonate in the sample - Mass of sodium bicarbonate reacted with acid
= 2.00766 g - 0.023915 mol * Molar mass of sodium hydroxide (40 g/mol)
= 2.00766 g - 0.9566 g = 1.05106 g.
Similarly, we can calculate the mass of sodium carbonate (Na₂CO₃) in the sample by subtracting the masses of sodium bicarbonate and sodium hydroxide from the total sample mass.
Mass of sodium carbonate = Sample mass - Mass of sodium bicarbonate - Mass of sodium hydroxide
= 3.00 g - 2.00766 g - 1.05106 g = 0.94128 g.
Finally, we can calculate the percentages of sodium hydroxide and sodium carbonate in the mixture:
Percentage of sodium hydroxide = (Mass of sodium hydroxide / Sample mass) * 100
Percentage of sodium hydroxide = (1.05106 g / 3.00 g) * 100 = 35.03%
Percentage of sodium carbonate = (Mass of sodium carbonate / Sample mass) * 100.
Percentage of sodium carbonate = (0.94128 g / 3.00 g) * 100 = 31.37%
The percentage of inerts = 100% - (31.37% + 35.03% ) = 100 - 66.4 = 33.6%
To learn more about mixture/percentage click on,
https://brainly.com/question/8560563
#SPJ4
How many minutes are there in 2.00 days
Answers
Answer:
2880
Step-by-step explanation:
Notes by the time while you buy 1440
Which of the following pairs of hypotheses are used to test if the mean of the first population is smaller than the mean of the second population, using independent random sampling?
H0: µ1-µ2 ≥ 0
HA: µ1-µ2 < 0
Answers
The pair of hypotheses used to test if the mean of the first population is smaller than the mean of the second population, using independent random sampling, is H0: µ1-µ2 ≥ 0 and HA: µ1-µ2 < 0.
The given pair of hypotheses represents a one-tailed test where we are interested in determining if the mean of the first population (µ1) is smaller than the mean of the second population (µ2).
The null hypothesis (H0) states that the difference between the means, represented by (µ1-µ2), is greater than or equal to zero. This means that there is no significant difference between the means or that the mean of the first population is equal to or greater than the mean of the second population.
The alternative hypothesis (HA) states that the difference between the means, represented by (µ1-µ2), is less than zero. This suggests that there is a significant difference between the means and specifically indicates that the mean of the first population is smaller than the mean of the second population.
By conducting a statistical test, such as a t-test or z-test, and analyzing the results, we can evaluate the evidence and make an inference regarding the relationship between the means of the two populations based on the given pair of hypotheses.
Learn more about hypothesis here:
https://brainly.com/question/30899146
#SPJ11
Answer this question to get brainlist

Answers
Answer:
The answer is D
Answer:
The answer is D
Step-by-step explanation:
A is incorrect because since 1 and 7 are both on the bottom half so they are congruentB is incorrect because 3 and 5 are both on the bottom half so they are congruent as wellC is incorrect for the same reason as A and BD is correct because they are both on the top half which means they cant be congruentThus your answer would be D
monitors manufactured by tsi electronics have life spans that have a normal distribution with a standard deviation of 1300 hours and a mean life span of 15,000 hours. if a monitor is selected at random, find the probability that the life span of the monitor will be more than 17,340 hours. round your answer to four decimal places.
Answers
The probability that the life span of the monitor will be more than 17,340 hours is approximately 0.0359, rounded to four decimal places.
We can use the standard normal distribution to solve this problem by standardizing the value of 17,340 hours to a z-score:
z = (17340 - 15000) / 1300 = 1.8
Using a standard normal distribution table or calculator, we find that the probability of getting a value greater than 1.8 is 0.0359.
Therefore, the probability that the life span of the monitor will be more than 17,340 hours is approximately 0.0359, rounded to four decimal places.
learn more about probability
https://brainly.com/question/30034780
#SPJ4
Answer the question above

Answers
Answer:
BA
Step-by-step explanation:
The hypotenuse is the longest side or opposite the right angle.
Answer:
AB
Step-by-step explanation:
The pythagorean theorem is AC² + CB² = AB²
AB represents the hypotenuse
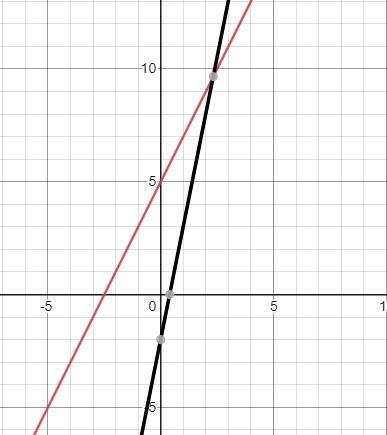
How many solutions does this have?
y=5x+-2
y=5--2x
Answers
Answer:
one solution (2.333, 9.6666)
Step-by-step explanation:
The ys have to be equal for there to be 1 solution. Let's see if they are. Equate the ys. - -2x becomes 2x
5x +-2 = 2x + 5 Write the left with 1 sign
5x - 2 = 2x + 5 Subtract 2x from both sides
2x 2x
3x - 2 = 5 Add 2 to both sides
2 2
3x = 7 Divide by 3
x = 7/3
x = 2 1/3
y = 5x - 2
y = 5(2 1/3) - 2
y = 11 2/3 - 2
y = 9 2/3
Define the term functions limits and continuity as used in
business calculus and use an example
Answers
In business calculus, the term "functions" refers to mathematical relationships that associate inputs (typically denoted as x) with corresponding outputs (typically denoted as y). Functions can represent various aspects of business operations, such as revenue, cost, profit, demand, and supply.
The concept of "limits" in calculus deals with the behavior of a function as the input approaches a particular value. It determines the value that the function approaches or tends to as the input gets arbitrarily close to a specified value. Limits are essential for analyzing the behavior of functions near certain points, understanding rates of change, and evaluating derivatives and integrals.
"Continuity" of a function refers to its smooth and unbroken nature, without any abrupt jumps, holes, or vertical asymptotes. A function is continuous if its graph can be drawn without lifting the pen from the paper. Continuity ensures that small changes in the input correspond to small changes in the output, which is crucial for reliable analysis and prediction.
For example, consider the function f(x) = 2x + 1. This linear function represents a business scenario where x represents the number of units sold, and f(x) represents the total revenue generated. The limit of f(x) as x approaches 2 is 5, indicating that as the number of units sold approaches 2, the total revenue approaches $5. Since f(x) = 2x + 1 is a linear function, it is continuous across its entire domain.
Learn more about functions, limits, and continuity in calculus here:
brainly.com/question/29297331
#SPJ11
Consider a competitive industry with a large number of firms, all of which have identical cost functions c(y) = 2y² +8 for y> 0 and c(0) = 0. Marginal cost is MC(y) = 4y. Suppose that initially the demand curve for this industry is given by D(p) = 20 - p (The output of a firm does not have to be an integer number, but the number of firms does have to be an integer) (a) What is the supply curve of an individual firm? If there are n firms in the industry, what will be the industry supply curve? (b) What is the smallest price at which the product can be sold? (c) What will be the equilibrium number of firms in the industry? equilibrium price? What will be the equilibrium output of each firm? equilibrium output of the industry? (d) Now suppose that the demand curve shifts to D(p) = 21 p. What will be the equilibrium number of firms? (Hint: Can a new firm enter the market and make nonnegative profits?) (e) With the new demand curve D(p) 21 p, what will be the equilibrium price? What will be the equilibrium output of each firm? What will be the equilibrium output of the industry? (f) Now suppose that the demand curve shifts to D(p) = 24 - p. What will be the equi- librium number of firms? What will be the equilibrium price? What will be the equilibrium output of each firm? What will be the equilibrium profits of each firm? = What will be the What will be the
Answers
The equilibrium number of firms will be the smallest integer such that the price is 6 or higher. This occurs when n = 2. At this equilibrium, the price is P = 6, the output of each firm is y = 3/2, the industry's output is Y = 3, and the profit of each firm = -2.
a) Supply curve of an individual firm
The price received by the individual firm will be P. Its demand curve is given by
D(p) = 20 - p.
Each firm chooses output to maximize its profit. Profit maximization occurs when the price is equal to the marginal cost. Mathematically,
P = MC(y)
4y = P
y = P/4
Thus the supply curve of the firm is y = P/4
b) The smallest price at which the product can be sold. The product can be sold at the minimum of the supply curve, which is y = 0, given P ≥ 0. Therefore the smallest price is P = 0.
c) Equilibrium price and output
Equilibrium occurs when each firm is producing at its profit-maximizing output given the output of other firms. Let the number of firms in the industry be n. The output of the industry is Y = ny. The industry supply curve is given by
S(P) = nP/4
The equilibrium price intersects the industry supply curve with the demand curve. Thus the equilibrium price satisfies
S(P) = Y
nP/4 = 20 - P
=> P = 80/(4 + n).
The equilibrium number of firms is the number that makes the industry supply curve equal to the demand curve. Thus
20 - P = nP/4
=> P = 80/(4 + n)
=> n = (80 - 20P)/P
= 20/P - 4.
Thus the equilibrium number of firms is a function of P and can range between 1 and infinity, but it must be an integer. The equilibrium output of each firm is given by
y = P/4 = 20/(4n + n²)
The equilibrium output of the industry is given by
Y = n
y = 5/P = (n² + 4n)/80.
d) Equilibrium number of firms with new demand curve D(p) = 21 - p.
The intersection of this curve with the marginal cost curve is at p = 21/5. This is greater than the minimum possible price of 0. Thus there is a positive profit to be earned in this industry, and new firms can enter the market.
e) Equilibrium price and output with new demand curve with the new demand curve D(p) = 21 - p, the industry supply curve and the equilibrium price are as given in part (d). The equilibrium output of each firm is given by y = P/4 = 21/20, and the equilibrium output of the industry is given by Y = 21/4.
f) Equilibrium number of firms, price, output, and profit with demand curve D(p) = 24 - p. This demand curve intersects the marginal cost curve at p = 6. The minimum possible price is P = 0. Thus there is a range of prices from 0 to 6 where firms can profit positively.
The equilibrium number of firms will be the smallest integer such that the price is 6 or higher. This occurs when n = 2. At this equilibrium, the price is P = 6, the output of each firm is y = 3/2, the output of the industry is Y = 3, and the profit of each firm is (6)(3/2) - (2)(2(3/2)² + 8) = -2.
To know more about the demand curve, visit:
brainly.com/question/13131242
#SPJ11
a box with a square base and an open top must have a volume of 4 m3 . find the height of the box that has the smallest possible surface area.
Answers
The height of the box that has the smallest possible surface area is 20m .
In the question ,
it is given that ,
the box has a square base ,
let the side of the box = "x" m
and let the height of the box = "y" m
volume of the box is given as 32000 m³,
So , x²y = 32000
y = 32000/x²
let the surface area of the box be "S" , that means
surface area(S) = area of base + total area of the 4 sides
= x²y + 4xy
Substituting the value of y = 32000/x² , we get
= x² + 4x(32000 / x²)
= x² + 128,000 / x, x > 0
to minimize the area we differentiate it with respect to x,
we get ,
= 2x - 128,000 / x²
= (2x³ - 128,000) / x²
Substituting S' = 0 , we get , 2x³ = 128,000
x³ = 64,000
x = 40
and y = 32000/(40)² = 20 m .
Therefore , The height of the box that has the smallest possible surface area is 20m .
The given question is incomplete , the complete question is
A box with a square base and open top must have a volume of 32,000 m³ . Find the height of the box that has the smallest possible surface area ?
Learn more about Surface Area here
https://brainly.com/question/28348566
#SPJ4
NEED HELP ASAP GIVING BRAINLEST!!!!!!
The sales tax in the town where Amanda lives is 5%. Amanda paid $25 in sales tax on a new stereo. What was the price of the stereo? The price of the stereo was $_______ .
Answers
Answer:
Its 514.23
Step-by-step explanation:
I just answered this question and I got it correct
HELP ASAP!!!
An investor bought 1,500 shares of stock for $6 a share. He estimates the probability that the stock will rise to a value of $25 a share is 24%, and the probability it will fall to $2 a share is 76%. What is the expected value of the investor's profit from buying the stock?
A: $13,560
B: $9,120
C: $6,720
D: $2,280
Answers
Please help explain and answer

Answers
2.4
3. 9
4. 1/2
5. 2/-9
6. -1
7. 1
8. 7/4
When finding slope you want to subtract Y1 - Y2 and X1 -X2 to get your answer
Solving proportions-what’s 3 over 7 and 12 over 21? do the ratios from a proportion
Answers
Answer:
3:7 and 12:21
6:14
9:21
12:28
No they do not for a proportion
Step-by-step explanation:
use the Simplex method to find the minimum value of the objective function w = 9x1 + 6x2 Subject to the constraints: x1 +2x2 ≥ 5 2x1 + 2x2 ≥ 8 2x2 +x2 ≥ 6 Where x1 ≥ 0 and x2 ≥ 0
Answers
The optimal solution is x1 = 4, x2 = 0, x3 = 1, w = 0, and the minimum value of the objective function is 0.
To solve this linear programming problem using the Simplex method, we first need to convert it into standard form by introducing slack variables.
Our problem can be rewritten as follows:
Minimize w = 9x1 + 6x2
Subject to:
x1 + 2x2 + x3 = 5
2x1 + 2x2 + x4 = 8
x1 + 2x2 + 2x3 = 6
where x1, x2, x3, and x4 are all non-negative variables.
Next, we set up the initial simplex tableau:
Basic Variables x1 x2 x3 x4 RHS
x3 1 2 1 0 5
x4 2 2 0 1 8
x5 1 2 2 0 6
z -9 -6 0 0 0
The last row represents the coefficients of the objective function. The negative values in the z-row indicate that we are minimizing the objective function.
To find the pivot column, we look for the most negative coefficient in the z-row. In this case, the most negative coefficient is -9, which corresponds to x1. Therefore, x1 is our entering variable.
To find the pivot row, we calculate the ratios of the RHS values to the coefficients of the entering variable in each row. The smallest positive ratio corresponds to the pivot row. In this case, the ratios are:
Row 1: 5/1 = 5
Row 2: 8/2 = 4
Row 3: 6/1 = 6
The smallest positive ratio is 4, which corresponds to row 2. Therefore, x4 is our exiting variable.
To perform the pivot operation, we divide row 2 by 2 to make the coefficient of x1 equal to 1:
Basic Variables x1 x2 x3 x4 RHS
x3 0 1 1 -1 1
x1 1 1 0 1/2 4
x5 0 1 2 -1 2
z 0 -3 9 9/2 -18
We repeat the process until all coefficients in the z-row are non-negative. In this case, we can stop here because all coefficients in the z-row are non-negative.
Therefore, the optimal solution is x1 = 4, x2 = 0, x3 = 1, w = 0, and the minimum value of the objective function is 0.
Learn more about value here:
https://brainly.com/question/30145972
#SPJ11
What is the additive inverse of –42?
Answers
Answer:
The additive inverse is 42
Step-by-step explanation:
The additive inverse is the number you add to get zero
-42+x = 0
Add 42 to each side
-42+x+42= 0+42
x = 42
The additive inverse is 42