8. Beatrice has 20 coins in quarters and nickels. The total value of her coins is $2.20. How many mickels and quartiers
does she have?
Answers
Answer:
40
Step-by-step explanation:
Answer:
6 quarters, 14 Nickels.
Related Questions
Select the correct answers. Which two words or phrases indicate a cause and effect relationship? O first of all O likewise O for this reason O before because
PLEASE HELP ASAP
Answers
Answer:
D. because
Step-by-step explanation:
ok
The 2008 world record for the men's 100-m dash was 9.72 s. The third-place runner crossed the finish line in 10.07 s. When the winner crossed the finish line, how far was the third-place runner behind him?
a) Compute an answer that assumes that each runner ran at his average speed for the entire race.
b) Compute another answer that assumes, that after an initial acceleration phase, world-class sprinters run at a speed of 12.0 m/s. If both runners in this race reach this speed, how far behind is the third-place runner when the winner finishes?
Answers
The third-place runner would have been 50.0 meters behind the winner when the winner crossed the finish line.
a) Computation on the assumption that each runner ran at his average speed for the entire race:
The difference in time between the winner and the third-place runner is 10.07 – 9.72 = 0.35 seconds.
Therefore, the third-place runner was behind the winner by a distance of:
(100 m)/(9.72 m/s – 10.07 m/s)
= 1,000 m/(-0.35 m/s)
≈ 285.7 m
(Note: The answer is negative because the third-place runner was behind the winner. The magnitude of the answer represents the distance that the third-place runner was behind the winner.)
b) Computation on the assumption that after an initial acceleration phase, world-class sprinters run at a speed of 12.0 m/s:
If the runners reach a constant speed of 12.0 m/s after an initial acceleration phase, then they will cover the first 50 meters in a time of t = d/v = 50 m/12.0 m/s = 4.17 s.
During this time, the winner would have covered an additional 50 meters and finished the race, while the third-place runner would have covered a distance of only d = v*t = 12.0 m/s x 4.17 s = 50.0 m.
So, the third-place runner would have been 50.0 meters behind the winner when the winner crossed the finish line.
To know more about average speed, visit:
https://brainly.com/question/13318003
#SPJ11
In the two scenarios, the third-place runner was 3.47m and 4.2m behind when the winner crossed the finish line, assuming constant average speed and a speed of 12m/s respectively.
Explanation:To answer this question, you need to understand the concept of average speed which is calculated by dividing the total distance traveled by the total time taken.
a) In the first scenario, assuming, both runners maintained a constant speed throughout the race. The speed of the winner is 100m / 9.72s = 10.28 m/s and the speed of the third-place runner is 100m / 10.07s = 9.93 m/s.
When the winner crossed the finish line, the third-place runner was still running for (10.07s - 9.72s) = 0.35s. At his average speed he was (9.93m/s * 0.35s) = 3.47m behind.
b) In the second scenario, if both runners reached the same speed of 12m/s after an initial acceleration phase, the time they spent at this speed will vary.
When the winner crossed the finish line, the third-place runner still needed (10.07s - 9.72s) = 0.35s to finish. At the speed of 12m/s, he was (12m/s * 0.35s) = 4.2m behind.
Learn more about Speed Calculation here:https://brainly.com/question/35969362
#SPJ12
Please help p l e a s e

Answers
Answer:
Step-by-step explanation:
1. 2x>-6
2. x-4<7
3. -x-5<=-2
4. 6+x<=3
hope this helps!
Answer:
1 2x>-6
2 x-4<-7
4 6+x _<_
3-x-5 _<_-2
Step-by-step explanation:
Find y as a function of t if 25y ′′
+81y=0 y(0)=5,y ′
(0)=7.
y(t)=
Find y as a function of t if y ′′
+12y ′
+37y=0,y(0)=7,y ′
(0)=4 y(t)=
Answers
For the differential equation 25y'' + 81y = 0 with initial conditions y(0) = 5 and y'(0) = 7, the solution is y(t) = 5cos(3t) + (7/3)sin(3t).
We are given the differential equation: y′′+12y′+37y=0
Step 1: Determine the characteristic equation by assuming that y=erty''+12y'+37y=0r2+12r+37=0
Step 2: Solve the quadratic equation to determine the roots of the characteristic equation.
We get: r=-6 ± 5i
Step 3: The general solution to the differential equation can be written as y(t)=c1e−6tc2cos(5t)+c3sin(5t)
where c1,c2, and c3 are constants that we need to solve using the initial conditions.
Step 4: We are given that y(0)=7 and
y'(0)=4.
Using these initial conditions, we can solve for the constants c1,c2, and
c3.c1=7
c2=0.8
c3=1.6
Thus the solution to the differential equation y′′+12y′+37y=0
with the initial conditions y(0)=7 and y′(0)=4 is:
y(t)=7e−6t+0.8cos(5t)+1.6sin(5t)
Therefore, the value of y(t) is 7e−6t+0.8cos(5t)+1.6sin(5t).
Learn more about quadratic equation from the given link:
https://brainly.com/question/30098550
#SPJ11
Suppose annual salaries for sales associates from a particular store have a bell-shaped distribution with a mean of $32,500 and a standard deviation of $2,500. Refer to Exhibit 3-3. The z-score for a sales associate from this store who earns $37,500 is
Suppose annual salaries for sales associates from a particular store have a bell-shaped distribution with a mean of $32,500 and a standard deviation of $2,500. Refer to Exhibit 3-3. The z-score for a sales associate from this store who earns $37,500 is
Answers
To find the z-score for a sales associate who earns $37,500, we can use the formula:
z = (x - μ) / σ
Where:
x is the value we want to convert to a z-score (in this case, $37,500),
μ is the mean of the distribution (in this case, $32,500), and
σ is the standard deviation of the distribution (in this case, $2,500).
Substituting the given values into the formula, we have:
z = (37,500 - 32,500) / 2,500
z = 5,000 / 2,500
z = 2
Therefore, the z-score for a sales associate who earns $37,500 is 2.
To learn more about mean visit;
brainly.com/question/31101410
#SPJ11
The z-score for a sales associate earning $37,500 in a system where the mean salary is $32,500 and the standard deviation is $2,500 has a z-score of 2. This score indicates that the associate's salary is two standard deviations above the mean.
Explanation:The z-score represents how many standard deviations a value is from the mean. In this case, the value is the salary of a sales associate, the mean is the average salary, and the standard deviation is the average variation in salaries.
We calculate the z-score by subtracting the mean from the value and dividing by the standard deviation, like so:
Z = (Value - Mean) / Standard Deviation
So, the z-score for an associate earning $37,500 would be:
Z = ($37,500 - $32,500) / $2,500
This gives us a z-score of +2, indicating that a salary of $37,500 is two standard deviations above mean.
Learn more about z-score calculation here:https://brainly.com/question/34836468
#SPJ12
a random sample of 100 people was taken. there were sixty people in the sample who favored candidate a. we are interested in determining whether or not the proportion of the population in favor of candidate a is significantly more than 50%. the p-value is
Answers
The p- value for the given sample and favored sample to determine the proportion is equal to 0.04135 which is statistically significantly , reject null hypothesis and accept alternative hypothesis.
As given in the question,
Sample size of people 'n' = 100
Number of favored candidates = 60
Success value 'p' = 60/100
= 0.60
1 - p = 1 - 0.60
= 0.40
Null hypothesis : H₀ > 50%
Alternative hypothesis : H₁ ≤ 50%
Test statistic :
Proportion of the population:
z = (p - \(\^{p}\) ) / √ p ( 1- p)/n
= ( 0.60 - 0.50)/ √ 0.60(0.40)/100
= 0.10/ √0.0024
= 0.10/0.049
= 2.04
p - value using table is equal to 0.04135
Significant level is 0.05
0.04135 < 0.05 .
Here conclusion is statistically significant, reject null hypothesis and accept alternative hypothesis.
Therefore, the p- value for the given sample and favored sample is equal to 0.04135 which is statistically significantly , reject null hypothesis and accept alternative hypothesis.
Learn more about p- value here
brainly.com/question/14790912
#SPJ4
Point M is the midpoint of line segment CD,
shown below.
What are the coordinates of point M?
C (6,10)
M
D (20, 18)
Answers
Answer:
M(13, 14)-------------------------
Each coordinate of the midpoint is the average of endpoints:
x = (6 + 20)/2 = 26/2 = 13y = (10 + 18)/2 = 28/2 = 14Therefore M is (13, 14).
HELP
I WILL GIVE YOU BRAINLIEST
Give the solution to this quadratic.
y = 3(x-1)^2
Answers
Answer:
y=3x^2-6x+3
Step-by-step explanation:
The ___ of a hyperbola is one of two points such that the difference of the distances from any point on the hyperbola to the foci is a constant.
Answers
The POINT of a hyperbola is one of two points such that the difference of the distances from any point on the hyperbola to the foci is a constant.
What is hyperbola?A hyperbola is a significant conic section in mathematics that is created by the intersection of a double cone with a plane surface, though not always at the center. A hyperbola is symmetric along its conjugate axis and resembles the ellipse in many ways. A hyperbola is subject to concepts like foci, directrix, latus rectus, and eccentricity. Examples of hyperbola that are frequently seen include the path taken by the tip of a sundial's shadow, the scattering trajectory of subatomic particles, etc.Here, we'll use instances that have been solved to better grasp the definition, formula, derivation, and standard forms of hyperbolas.Hence, The POINT of a hyperbola is one of two points such that the difference of the distances from any point on the hyperbola to the foci is a constant.
learn more about hyperbola click here:
https://brainly.com/question/16454195
#SPJ4
evaluate the definite integral by interpreting it in terms of areas. ∫ 7 3 ( 5 x − 20 ) d x ∫37(5x-20)dx
Answers
To evaluate the definite integral ∫ 7 3 ( 5 x − 20 ) d x ∫37(5x-20)dx in terms of areas, we can interpret it as the area bounded by the x-axis, the line y=5x-20, and the vertical lines x=3 and x=7.
Using the power rule of integration, we can first simplify the integrand:
∫ 7 3 ( 5 x − 20 ) d x = ∫ 7 3 5 x d x − ∫ 7 3 20 d x
= [ 5 2 x 2 ] 7 3 − [ 20 x ] 7 3
= ( 5 2 ( 7 2 − 3 2 ) ) − ( 20 ( 7 − 3 ) )
= 70
Therefore, the definite integral evaluates to 70, which represents the area of the region bounded by the x-axis, the line y=5x-20, and the vertical lines x=3 and x=7.
Learn more about the definite integral :
https://brainly.com/question/29974649
#SPJ11
use the laplace transform and the procedure outlined in example 10 to solve the given boundary-value problem. y′′ +2y′+ y = 0, y′(0) = 6, y(1) = 6y(t) = ?
Answers
By applying the Laplace transform to the given boundary-value problem and following the procedure outlined in Example 10, the solution for y(t) is obtained as y(t) = 6e^(-t).
The Laplace transform can be used to solve differential equations, including boundary-value problems. In this case, we have the second-order linear homogeneous differential equation y'' + 2y' + y = 0, with the initial conditions y'(0) = 6 and y(1) = 6.
To solve the problem using the Laplace transform, we apply the transform to the differential equation and the initial conditions. This transforms the differential equation into an algebraic equation that can be solved for the Laplace transform of y(t), denoted as Y(s).
By applying the Laplace transform to the given differential equation, we obtain the algebraic equation s^2Y(s) + 2sY(s) + Y(s) = 0. Solving this equation for Y(s), we find Y(s) = 6s/(s^2 + 2s + 1).
To find the inverse Laplace transform of Y(s) and obtain the solution y(t), we use partial fraction decomposition and consult Laplace transform tables. By applying the inverse Laplace transform, we find y(t) = 6e^(-t).
Therefore, the solution for the given boundary-value problem is y(t) = 6e^(-t)
Learn more about Laplace transform here:
https://brainly.com/question/30759963
#SPJ11
Does this set of pairs of points pass the vertical line test? If it does, answer yes. If it does not pass the vertical line test, then give the input value for which the vertical line test fails.
{(2,3),(−2,0),(3,4),(5,9),(2,−1)}
Answers
Please see the attached image.

the function below is to be fit to a data set using linear regression. the correct linearization of the data needed to calculate the model coefficients a and b is:
Answers
The function below is not provided in the question, therefore, I cannot provide a specific linearization method to fit the data to a linear regression model.
However, in general, the correct linearization method for a function to be fit to a data set using linear regression would depend on the functional form of the equation.
For example, if the function is exponential, taking the logarithm of the data may result in a linear relationship that can be fit using linear regression.
The specific linearization method to fit a function to a linear regression model would depend on the functional form of the equation. For an exponential function, taking the logarithm of the data may result in a linear relationship that can be fit using linear regression. However, since the function in question is not provided, I cannot provide a specific linearization method.
The correct linearization method for a function to be fit to a linear regression model depends on the functional form of the equation and cannot be determined without knowledge of the specific function.
To know more about linear visit:
brainly.com/question/31510530
#SPJ11
Greg had a full carton of eggs. He used 1 over 3 of the eggs for a cake. Then he used 1 egg for an omelet.
Answers
The optimal amount of x1, x2, P1, P2 and income are given by the
following:
x1= 21/ 7p1 x2= 51 / 7p2
The original prices are: P1=10 P2=5 The original income is: I
=4189 The new price of P1 is the foll
Answers
The total change in the consumed quantity of x₁ as per given price and income is equal to 213.
x₁ = (21/7)P₁
x₂ = (51/7)P₂
P₁ = 10
P₂ = 5
P₁' = 81
To calculate the total change in the quantity consumed of x₁ when the price of P₁ changes from P₁ to P₁',
The difference between the quantities consumed at the original price and the new price.
Let's calculate the quantity consumed at the original price,
x₁ orig
= (21/7)P₁
= (21/7) × 10
= 30
x₂ orig
= (51/7)P₂
= (51/7) × 5
= 36.4286 (approximated to 4 decimal places)
Now, let's calculate the quantity consumed at the new price,
x₁ new
= (21/7)P1'
= (21/7) × 81
= 243
x₂ new
= (51/7)P2
= (51/7) × 5
= 36.4286
The total change in the quantity consumed of x₁ can be calculated as the difference between the new quantity and the original quantity,
Change in x₁
= x₁ new - x₁ original
= 243 - 30
= 213
Therefore, the total change in the quantity consumed of x₁ is 213.
learn more about change here
brainly.com/question/32782775
#SPJ4
The above question is incomplete, the complete question is:
The optimal amount of x1, x2, P1, P2 and income are given by the following:
x1= 21/ 7p1 x2= 51 / 7p2
The original prices are: P1=10 P2=5 The original income is: I =4189 The new price of P1 is the following: P1'=81 Assume that the price of x1 has changed from P1 to P1'. What is the total change in the quantity consumed of x1?
Please answer step by step
29 less than -10 times a number is equal to -18 times the number plus 91
Answers
Answer:
-10x - 29 = -18x + 91
x = 15
Step-by-step explanation:
29 less than -10 times a number is equal to -18 times the number plus 91:
-10x - 29 = -18x + 91
add 21 to both sides:
-10x - 29 + 29 = -18x + 91 + 29
-10x = -18x + 120
add 18x to both sides:
-10x + 18x = -18x + 120 + 18x
8x = 120
divide both sides by 8:
8x/8 = 120/8
x = 15
Please Solve. First answer with explanation gets Most Brainliest and Points. TYSM

Answers
Answer:
2x+10+x+5=180
3x+15=180
3x=165
x=55
hope this helps
have a good day :)
Step-by-step explanation:
anne can make 4 pizzas or 6 salads in an hour. bob can make 10 pizzas or 8 salads in an hour. which of the following is incorrect
Answers
Answer:I would think bobs thing..
Step-by-step explanation:
no one can make that many pizzas.
498,147,846,267
+ 32,870,714,538
Answers
Answer:
531018560805
Step-by-step explanation:
what is 2/5 close to?
Answers
An experiment was conducted to compare the alcohol content of soy sauce on two different production lines. Production was monitored eight times a day. The data are shown below. Assume both populations are normal. It is suspected that production line 1 is not producing as consistently as production line 2 in terms of alcohol content. Test the hypothesis that 01 = 02 against the alternative that 01702. Use a P-value. Production line 1: 0.48 0.39 0.42 0.52 0.39 0.49 0.52 0.51 Production line 2: 0.39 0.38 0.39 0.41 0.38 0.39 0.41 0.39 Calculate the test statistic. f= (Type an integer or a decimal. Round to two decimal places as needed.)
Answers
The p-value is less than 0.01, which is less than the significance level of 0.05. Hence, we reject the null hypothesis The t-value for a two-tailed test is 2.145
The given data is to test the hypothesis that production line 1 is not producing as consistently as production line 2 in terms of alcohol content against the alternative that μ₁ ≠ μ₂. Here, the population standard deviation is not given, so we will use the two-sample t-test formula that uses sample standard deviations to estimate the population standard deviations.
Sample 1: Production line 1: 0.48 0.39 0.42 0.52 0.39 0.49 0.52 0.51 Sample 2: Production line 2: 0.39 0.38 0.39 0.41 0.38 0.39 0.41 0.39 Here, we will use the two-sample t-test formula that uses sample standard deviations to estimate the population standard deviations.
The formula to find the t-test is given by:\($$t = \frac{\bar{X_1} - \bar{X_2}}{\sqrt{\frac{{S_1}^2}{n_1} + \frac{{S_2}^2}{n_2}}}$$\)where, \($$\bar{X_1}$$\) and \($$\bar{X_2}$$\) are the means of the two samples, \($$S_1$$\) and \($$S_2$$\)are the standard deviations of the two samples, and \($$n_1$$ and $$n_2$$\) are the sample sizes of the two groups.
Now, let us substitute the above values in the formula to calculate the test statistic.f= 3.45 (approx)Thus, the test statistic for the given data is 3.45.The two-sample t-test is used to test whether the means of two populations are equal or not.
The test statistic is calculated and compared with the critical value of t from the t-distribution. The p-value is the probability of getting the observed difference between means assuming the null hypothesis is true. Here, the calculated test statistic value is 3.45.
Now, we need to find out the degrees of freedom (df) using the formula:df = (n1 + n2) – 2= (8 + 8) – 2= 14 Now, we will look into the t-distribution table to find out the t-value for a two-tailed test with α = 0.05 and df = 14. . Here, since the calculated test statistic value is greater than the t-value, we reject the null hypothesis.
The p-value for a two-tailed test is the probability of observing a t-value greater than 3.45 or less than -3.45 with 14 degrees of freedom. The p-value is less than 0.01, which is less than the significance level of 0.05. Hence, we reject the null hypothesis and conclude that there is sufficient evidence to suggest that the alcohol content of production line 1 is different from that of production line 2. The t-value for a two-tailed test with α = 0.05 and df = 14 is 2.145
Know more about probabilities here:
brainly.com/question/29381779
#SPJ11

Q.1) If a²+b² = 73 and ab = 24, find (i) a+b (ii) a-b
Answers
Step-by-step explanation:
Given:
a² + b² = 73 and ab = 24We know that:
(a + b)² = a² + 2ab + b²
Now , substituting the value in equation,we get.
=> (a + b)² = 73 + 2 × 24
=> (a + b)² = 73 + 48
=> (a + b)² = 121
=> (a + b) = √121 = ±11. ----------(1)
Again:
(a - b)² = a² - 2ab + b²
=> (a - b)² = 73 - 48
=> (a - b)² = 25
=> (a - b)² = √25 = ±5. -------(2)
Hope this helps!
Step-by-step explanation:
the answer is in the image above
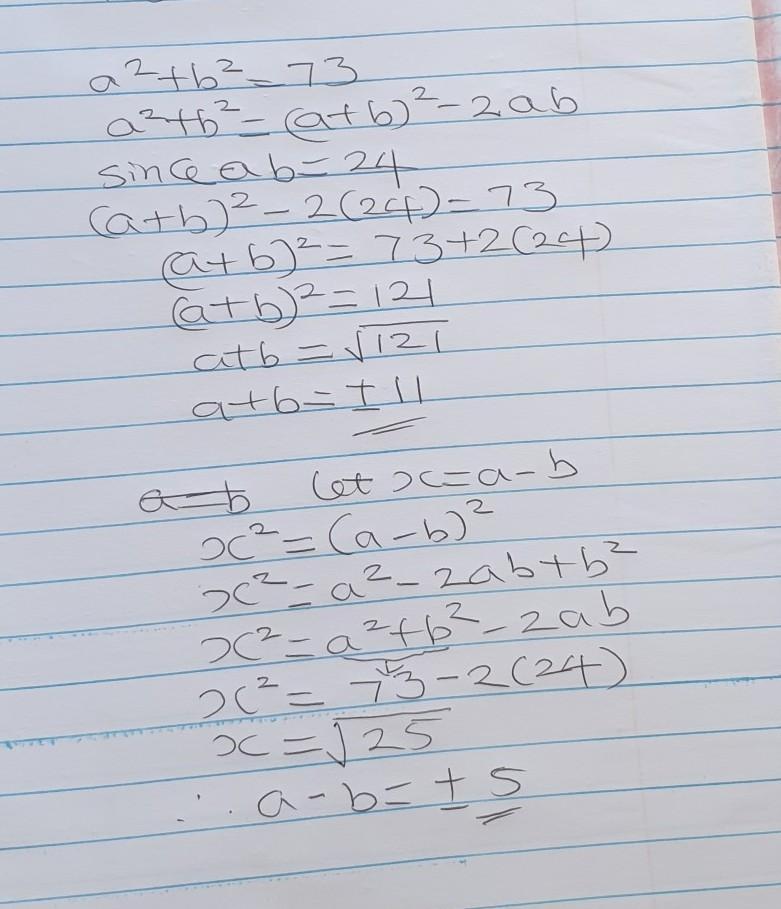
For a Student's t-distribution with mean 0, standard deviation 1, and degrees of freedom 49, which of the following Python lines outputs the probability P(t > 0.115)?
Answers
The following line of code in Python calculates the probability P(t > 0.115) for a Student's t-distribution with mean 0, standard deviation 1, and 49 degrees of freedom:
import scipy.stats as stats
1 - stats.t.cdf(0.115, df=49)
The cdf function calculates the cumulative density function (CDF) of the t-distribution, which gives the probability that the random variable (t-statistic) is less than or equal to a given value. To find the probability that it is greater than a given value, we subtract the CDF from 1.
Standard deviation is a statistical measure that calculates the amount of variation or dispersion of a set of data values. It represents how far the data points in a set deviate from the mean.
A low standard deviation indicates that the data points are close to the mean, while a high standard deviation indicates that the data points are more spread out.
To know more about standard deviation refer to:
brainly.com/question/23907081
#SPJ4
When Mark was looking at his monthly utility payments, he noticed that one payment was significantly lower than all the others. Which of the following would be most affected by Mark's observation? The median, average, highest, most frequent monthly payment
Answers
Answer:
The average monthly payment would be most affected by Mark's observation of one significantly lower payment. The reason is that the average is calculated by summing all the payments and dividing by the total number of payments, so any extreme values (such as the significantly lower payment) can have a substantial impact on the average value.
Step-by-step explanation:
Whats 42.12500 rounded to the nearest whole number?
Answers
answer this question step by step

Answers
I hope this help you


At a local college, 100 students were asked about their major fields of study. The results are shown
below. What is the probability that a randomly selected student is a female or a liberal arts major?
Majors at Local College
Mathematics/science Liberal Arts
16
20
15
18
Business Studies
14
17
Male
Female
19
50
Done

Answers
7/10 would be the probablity
7/10 is the probability that a randomly selected student is a female or a liberal arts major.
Let us determine the number of female students:
15 + 18 + 17 = 50.
Determine the number of students majoring in liberal arts:
20 + 18 = 38.
Determine the number of students who are both female and liberal arts majors: 18.
Add the number of female students and the number of liberal arts majors, but subtract the overlap (students who are both female and liberal arts majors):
50 + 38 - 18
= 70.
Divide the result by the total number of students:
70 / 100
= 7/10.
Hence, the probability that a randomly selected student is a female or a liberal arts major is 7/10.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ6
5 + m > -2 OR 2m < -20

Answers
Answer:
m > -7 OR m < -10
Step-by-step explanation:
5 + m > -2
5 + m + 2 > 0
5 + 2 > - m
7 > -m
-7 > m
2m < -20
m < -20 / 2
m < -10
¿Cuál de las siguientes fracciones algebraicas se puede reducir?
A.
8−x9−16x2
B.
5−x25−x2
C.
x2+4x−5x2−4
D.
3x2x2+8
Answers
Think About the Process Use the algebra tiles to help you solve the equation 4x - 12 = 20. What is
the first step in solving the equation using algebra tiles? What is the solution to the equation?
What is the first step in solving the equation using algebra tiles?
O A. Add twelve + 1 tiles to each side of the model.
OB. Divide each side of the model by 4.
OC. Multiply each side of the model by 4.
OD. Add twelve - 1 tiles to each side of the model.
Answers
The first step in solving the equation 4x - 12 = 20 using algebra tiles is to add twelve + 1 tiles to each side of the model.
By adding twelve + 1 tiles to each side of the model, we are essentially adding 12 to both sides of the equation.
This step helps to isolate the variable term, 4x, on one side of the equation and move the constant term, 12, to the other side.
After adding twelve + 1 tiles to each side, the equation becomes
4x = 32
Now, we can move on to solving for x by performing subsequent steps such as dividing both sides by 4 to isolate x.
In summary, the first step in solving the equation 4x - 12 = 20 using algebra tiles is to add twelve + 1 tiles to each side of the model.
To learn more about algebra tiles visit:
brainly.com/question/31274000
#SPJ11