8. What is 3x times (3x² - 5)?
a.3x² + 5x -5
b.9x³-5
c.9x³ - 15x
d.15x³ - 25x
Answers
Answer:
9x^3-15x
Step-by-step explanation:
Related Questions
2
5. Many people believe that criminals who plead guilty tend to get lighter sentences than those
who are convicted in trials. The accompanying table summarizes randomly selected sample
data for defendants in burglary cases in a specific city. All of the subjects had prior prison
sentences. Use a 0.05 significance level to find the critical value needed to test the claim that
the sentence (sent to prison or not sent to prison) is independent of the plea.
Sent to prison
Not sent to prison
Guilty Plea
392
564
Not-Guilty Plea
58
14
(1 point)09.488
03.841
042.557
05.991
Answers
Answer:
Is 03.841
Step-by-step explanation:
To find the critical value needed to test the claim that the sentence is independent of the plea, we need to perform a chi-square test of independence. The critical value is based on the significance level (α) and the degrees of freedom.
In this case, the given significance level is 0.05. Since the table represents a 2x2 contingency table (two categories for plea and two categories for sentence), the degrees of freedom (df) can be calculated as (number of rows - 1) * (number of columns - 1) = (2 - 1) * (2 - 1) = 1.
To find the critical value at a significance level of 0.05 with 1 degree of freedom, we consult a chi-square distribution table or use statistical software.
The critical value for a chi-square test with 1 degree of freedom and a significance level of 0.05 is approximately 3.841.
Therefore, the correct answer is 03.841.
Water works commission assume population standard deviation is 1.7 gallons. 15.8 gallons a day for sample of 249 families. Construct 80% confidence intervals
Answers
The 80% confidence interval for the average water usage of 249 families is (15.42, 16.18) gallons.
To construct an 80% confidence interval for the average water usage of 249 families, we can use the following formula:
CI = X ± t(α/2, df) * (s/√n)
where X is the sample mean (15.8 gallons), t(α/2, df) is the critical t-value from the t-distribution table at the desired confidence level and degrees of freedom (247 in this case), s is the population standard deviation (1.7 gallons), and n is the sample size (249).
At an 80% confidence level and 247 degrees of freedom, the critical t-value is approximately 1.296.
Plugging in the values, we get:
CI = 15.8 ± 1.296 * (1.7/√249)
CI = 15.8 ± 0.38
Therefore, the 80% confidence interval for the average water usage of 249 families is (15.42, 16.18) gallons.
This means that we are 80% confident that the true average water usage of the population lies within this interval.
To learn more about confidence interval click on,
https://brainly.com/question/17014802
#SPJ1

Anyone want to try this?
I’ll give the answer later.
If your try doing this then... good luck! :)

Answers
Answer:
D
Step-by-step explanation:
Volume of cylinder = Base x height
Base = πr^2 = 25π
Volume = 25π x 10 = 250π
Volume of cone = 1/3 Base x height
= 1/3 x 25π x 5 = 125π/3
Volume of silo = cylinder + cone + cone
= 250π + 125π/3 + 125π/3
= 785.4 + 130.9 + 130.9
= 1047.2
what is the value of -2/3x0.6÷ 6/5
Answers
Answer:
-0.33333333333 in other word it o.3 with line over 3
Step-by-step explanation:
-4x + 21 > -3
What could x be??
Answers
Answer:
x < 6
Step-by-step explanation:
subtract 21 on both sides
-4x > -24
divide both sides by -4 and flip the sign (bc you're dividing by a negative)
x < 6
Find a • b. a = <5, 2>, b = <4, 5> (2 points) a <20, 10> b <9, 7> c -10 d 30
Answers
The dot product of vectors a and b is option D. 30.
How did we get the value?To find the dot product of two vectors, you need to multiply their corresponding components and then sum the results.
Let's calculate the dot product of vectors a = <5, 2> and b = <4, 5>:
a • b = (5 x 4) + (2 x 5)
= 20 + 10
= 30
Therefore, the dot product of vectors a and b is 30.
learn more about product of vectors: https://brainly.com/question/30394406
#SPJ1
3. Kasey Marsenburg is a financial consultant for ABC Finance.
She eams $748.00 weekly. Her annual group medical coverage
costs $9.560, of which ABC Finance pays 65%. How much is
deducted weekly from her paycheck for medical coverage?
Answers
Answer:
Step-by-step explanation:
100-65=35%
Identify the range of the function shown in the graph.

Answers
Answer:
Identify the range of the function shown in the graph.
Answer:
range=(10, 8, 6, 4, 2, 0, -2, -4, -6, -8, -10)
Rearrange the equation so uuu is the independent variable.
-12u+13=8w-3
Answers
Answer:
u = 8w-16 /-12 or = - 8w-16/12 both mean the same due to the a/-b- = -a/b rule. Then you can factor out the rest. note the fnew subtraction changes mean the same as - (a/b) and should show without brackets as a centre pointing whole fraction subtraction sign.
Step-by-step explanation:
-12u -13 = 8w-3
-12u+13 -13 = 8w-3-13 Eliminate -13 by +13 both sides
-12u = 8w-16 So you are left with one value left side.
-12u/-12 = 8/-12 - 16/-12 Then divide all values by -12 to find value for u and keep the subtraction as 8 never had subtraction sign and no multiplication .
u = 8w-16 /-12 Then you can factor out the rest
This has made u the independent variable then you have a choice to continue showing or ignore u; as u =
= - 8(w-2)/12 Step 1 Factor with subtraction change from -12 to - central fraction
= - 2(w-2)/3 Step 2 Simplify with new minus sign for central fraction to replace a/-b
Answer:
The answer is W = -3/2u + 2
Step-by-step explanation:
Look at attachment:
Hope this helps! :)

Help please!!!!!!
!!!!!

Answers
Answer: GL = \(\sqrt{61}\)
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean theorem. GL is the hypotenuse.
Given:
a² + b² = c²
Substitue:
AL² + AG = GL²
Find side lengths (count via the coordinate plane given):
6² + 5² = GL²
Square:
36 + 25 = GL²
Add:
61 = GL²
Square root both sides:
\(\sqrt{61}\) = GL
This question has two parts. First, answer Part A. Then, answer Part B. The question is below


Answers
Both relation (year, percent of men) and (year, percent of women) are functions.
What is a function?
A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets; mapping from A to B will be a function only when every element in set A has one end, only one image in set B.
Now,
In given data
For every input (i.e. year) there is a unique output (i.e. percent of men/ percent of women)
Hence, Given relation (year, percent of men) and (year, percent of women) are functions.
To know more about functions visit the link
https://brainly.com/question/12431044?referrer=searchResults
#SPJ1
The product of a number and 1.5 is less than the absolute value of the difference between 20 and 5. What are all the possible values of the number?
Show your work.

Answers
Answer:
any value less than 10
Step-by-step explanation:
Let x represent the number.
1.5x < |20 -5|
1.5x < 15 . . . . simplify
x < 10 . . . . . . divide by 1.5
The number may be any value less than 10.
Two UNO students want to start a business selling slushies at the Gene Leahey Mall during the summer. They will have an initial cost of $500 to buy equipment and an additional $1.25 cost for each slushie they sell. They
plan to charge $3.50 for each slushie. Let C(x) represent the cost (in dollars) associated with starting and running the business and R(x) represent the revenue (in dollars) earned from sales. Let x represent the number
of slushies sold.
a. Write a linear function for cost.
C(x) =
b. Write a linear function for revenue.
R(x) =
Answers
Part (a)
The cost is the initial cost plus the cost per slushie multiplied by the number of slushies sold.
\(C(x)=500+1.25x\)
Part (b)
The revenue is the number of slushies sold multiplied by the amount charged per slushie.
\(R(x)=3.50x\)
there are 3 arms for every 2 eyes. If there are 6 eyes, how many arms are there?
Answers
Answer:
There are 9 arms.
Step-by-step explanation:
A bag contains 6blue marbles 8 green marbles 9 red marbles and 17 yellow marbles what is the ratio of blue marbles to Total marbles
Answers
Answer:
6:40
Step-by-step explanation:
6 blue marbles
8 green marbles
9 red marbles
17 yellow marbles
6+8+9+17= 40.
40 is the total amount of marbles.
There are 6 blue marbles.
Comparing the amount of 6 to 40 would be 6:40
(3/4)x=3 how do you solve for x with fractions?
Answers
Answer:
x = 4
Step-by-step explanation:
Dividing by a fraction is the same as multiplying by the reciprocal of the fraction. For example, m÷(2/3) = m×3/2

Answer:
X=4 I'm not sure what you mean by solve with fractions, but I now the answer is right.
Step-by-step explanation:
3 ÷ 3/4 =4
or
3/4=9/12
3=36/12
36/12÷9/12=4
PLS 50PTS
WILL MARK AS BRAINLIEST
A fair die is tossed once. What is the probability that it shows 3?
Answers
Answer: 1/6
Step-by-step explanation:
There are 6 faces in a dice
The faces are labeled as =
1
2
3
4
5
6
This means, there are 6 different outcomes in a dice
So we have to find out the probability of the dice showing 3
Now, out of 6 different possible outcomes, there is only 1 face labeled as 3.
So there is only 1 possible outcome as "3".
We can simply make it a fraction = 1/6 .
So the answer is 1/6
Probability is expressed as a fraction, percentage and decimal.
Find the equation of the ellipse, centre and directrices given that the end points of the major axis are (4,1) and (8,1) and the eccentricity is 1/3
Answers
The equation of the ellipse is (x - 6)² / 4 + (y - 1)² / (16/9) = 1, the center is (6,1), and the directrices are x = 0 and x = 12.
How to explain the equationThe center of the ellipse is the midpoint of the major axis. The midpoint of the line segment connecting (4,1) and (8,1) is ((4+8)/2, (1+1)/2) = (6,1). Therefore, the center of the ellipse is (6,1).
The distance between the center and one of the vertices (say, (8,1)) is the length of the semi-major axis, a. This distance is (8-6) = 2. Therefore, the semi-major axis is a = 2.
The eccentricity, e, is given as 1/3.
The distance between the center and one of the foci, c, is related to the semi-major axis and eccentricity by the equation c = ae. Plugging in the values we know, we get c = (1/3)(2) = 2/3.
We can write the equation of the ellipse in standard form:
(x - 6)² / 2² + (y - 1)^2 / b² = 1
where b is the semi-minor axis. We can solve for b using the relationship between the semi-major axis, semi-minor axis, and eccentricity:
So the equation of the ellipse is:
(x - 6)² / 4 + (y - 1)² / (16/9) = 1
The directrices are located a distance of a² / c = (2²) / (2/3) = 6 units away from the center along the major axis. These are the lines x = 6 - 6 = 0 and x = 6 + 6 = 12.
Learn more about equations on;
https://brainly.com/question/2972832
#SPJ1
Use the image to determine the direction and angle of rotation. Graph of triangle ABC in quadrant 1 with point A at 1 comma 3. A second polygon A prime B prime C prime in quadrant 4 with point A prime at 3 comma negative 1. 90° clockwise rotation 180° clockwise rotation 180° counterclockwise rotation 90° counterclockwise rotation
Answers
First, we can find the translation vector that moves point A to point A':
translation vector = A' - A = (3, -1) - (1, 3) = (2, -4)
Next, we can find the vector that connects point B to point A in the original triangle ABC:
vector AB = B - A
Then, we can rotate this vector using the rotation matrix for the desired angle of rotation:
90° clockwise rotation:
|0 -1| |x| |y'|
|1 0| * |y| = | -x'|
180° clockwise rotation:
|-1 0| |x| |x'|
| 0 -1| * |y| = |y'|
180° counterclockwise rotation:
|-1 0| |x| |-x'|
| 0 -1| * |y| = |-y'|
90° counterclockwise rotation:
| 0 1| |x| |-y'|
|-1 0| * |y| = | x'|
Finally, we can add the translation vector to the rotated vector to get the coordinates of the corresponding point in the new polygon A' B' C':
90° clockwise rotation: B' = A' + (AB rotated 90° clockwise + translation)
180° clockwise rotation: B' = A' + (AB rotated 180° clockwise + translation)
180° counterclockwise rotation: B' = A' + (AB rotated 180° counterclockwise + translation)
90° counterclockwise rotation: B' = A' + (AB rotated 90° counterclockwise + translation)
Using this method, we can find the coordinates of points B' and C' in the new polygon A' B' C'. Then, we can use the coordinates of these points to determine the direction and angle of rotation needed to move the original triangle to the new polygon.
Which algebraic expression is equivalent to the expression below?
(3n+13) + (6+7n)
A. 9n + 20
B. 16n + 13
C. 10n + 19
D. 22n + 7
Answers
Answer: C) 10n +19
Step-by-step explanation:
Let's simplify the provided expression (3n+13) + (6+7n)
Since this is just addition we can just remove the parenthesis and use the commutative property to make adding easier
3n+13+6+7n
3n+7n+13+6
10n+19
8x + 9y - 6x - 3y i forgot how to do these lol
Answers
if the XY plane above shows one of the two points of intersection on the graphs of a linear function in a quadratic function, the shown point of intersection has coordinates, parentheses V, W parentheses. If the vertex of the graph of the quadratic function is a parentheses four, 19 parentheses, what is the value of v
Answers
Therefore, the point (v, w) = (x, y) = (6, 15)
How to solveThe diagram above has two graphs (ABC and DE) intercepting at a point, (v, w).
To find the interception point (v, w), we need to first find the equations of each graph, with ABC being a parabola and DE, a straight line.
Since ABC is a parabola and the vertex is given, the standard vertex form of a parabola is given by:
y = a(x – h)2 + k ----------- eqn(1)
where (h, k) is the vertex of the parabola (the vertex is the point where the parabola changes direction) and "a" is a constant that tells whether the parabola opens up or down (negative indicates downward and positive indicates upward).
Given vertex (4, 19), eqn(1) becomes:
y = a(x - 4)2 + 19 -------------- eqn(2)
Since the parabola passes through point (0, 3), that is, x = 0 and y = 3,
we substitute the value of x and y into eqn(2) to find the value of "a"
3 = a(0 - 4)2 + 19
3 = a(-4)2 + 19
3 = 16a + 19
16a = 3 - 19
16a = -16
a = -1
Thus, eqn(2) becomes:
y = -(x - 4)2 + 19 ------------- eqn(3)
Next, we find the equation of DE (straight line).
Since DE is a straight line and the general form of straight-line equation is given by:
y = mx + c ------------------ eqn(4)
where m is the slope and c is the point at which the graph intercepts the y-axis.
c = -9
m = (y2 - y1) / (x2 - x1)
At points (0, -9) and (2, -1)
x1 = 0
x2 = 2
y1 = -9
y2 = -1
m = (-1 - (-9)) / (2 - 0)
= (-1 + 9)/2
= 8/2
m = 4
Substitute the values of m and c into eqn(4)
y = 4x - 9 ---------------- eqn(5)
Since point (v, w) is the point where both graphs meet,
eqn(3) = eqn(5)
-(x - 4)2 + 19 = 4x - 9
-[(x - 4)(x - 4)] + 19 = 4x - 9
-(x2 - 8x + 16) + 19 = 4x - 9
-x2 + 8x - 16 + 19 = 4x - 9
-x2 + 8x - 4x - 16 + 19 + 9 = 0
-x2 + 4x + 12 = 0
multiply through with -1
x2 - 4x - 12 = 0 ----------- eqn(6)
The above is a quadratic equation and can be simplified either by factorization, completing the square, or quadratic formula method.
Using the factorization method,
product of roots = -12
sum of roots = -4
Next, find two numbers whose sum is equal to the sum of roots (-4) and whose product is equal to the product of roots (-12)
Let the two numbers be 2 and -6
Replace the sum of roots (-4) in eqn(6) with the two numbers
x2 - 6x + 2x - 12 = 0
Group into two terms
(x2 - 6x) + (2x - 12) = 0
factorize each term
x(x - 6) + 2(x - 6) = 0
Pick and group the two values outside each bracket and inside one of the brackets
(x + 2) (x - 6) = 0
x + 2 = 0 and x - 6 = 0
x = -2 and x = 6
Since the point, (v, w) is on the right side of the y-axis, it follows that x cannot be –2. Therefore, x = 6.
substitute the value of x into eqn(5)
y = 4(6) - 9
y = 24 - 9
y = 15
Therefore, the point (v, w) = (x, y) = (6, 15)
Read more about quadratic function here:
https://brainly.com/question/29293854
#SPJ1

FOR 100 POINTS!!!!!!!!!!!
A food truck did a daily survey of customers to find their food preferences. The data is partially entered in the frequency table. Complete the table to analyze the data and answer the questions:
Likes hamburgers Does not like hamburgers Total
Likes burritos 29 41
Does not like burritos 54 135
Total 110 205
Part A: What percentage of the survey respondents liked neither hamburgers nor burritos? Show all work. (3 points)
Part B: What is the marginal relative frequency of all customers who like hamburgers? Show all work. (3 points)
Part C: Is there an association between liking burritos and liking hamburgers? Use ratios of joint and marginal frequencies to support your answer. (4 points)
Answers
Answer:
Part A:
To find the percentage of survey respondents who liked neither hamburgers nor burritos, we need to calculate the frequency in the "Does not like hamburgers" and "Does not like burritos" categories.
Frequency of "Does not like hamburgers" = Total in "Does not like hamburgers" category = 135
Frequency of "Does not like burritos" = Total in "Does not like burritos" category = 54
Total respondents who liked neither hamburgers nor burritos = Frequency of "Does not like hamburgers" + Frequency of "Does not like burritos" = 135 + 54 = 189
Percentage of survey respondents who liked neither hamburgers nor burritos = (Total respondents who liked neither hamburgers nor burritos / Total respondents) x 100
Percentage = (189 / 205) x 100 = 92.2%
Therefore, 92.2% of the survey respondents liked neither hamburgers nor burritos.
Part B:
To find the marginal relative frequency of all customers who like hamburgers, we need to divide the frequency of "Likes hamburgers" by the total number of respondents.
Frequency of "Likes hamburgers" = 110 (given)
Total respondents = 205 (given)
Marginal relative frequency = Frequency of "Likes hamburgers" / Total respondents
Marginal relative frequency = 110 / 205 ≈ 0.5366 or 53.66%
Therefore, the marginal relative frequency of all customers who like hamburgers is approximately 53.66%.
Part C:
To determine if there is an association between liking burritos and liking hamburgers, we can compare the joint and marginal frequencies.
Joint frequency of "Likes hamburgers" and "Likes burritos" = 29 (given)
Marginal frequency of "Likes hamburgers" = 110 (given)
Marginal frequency of "Likes burritos" = 70 (calculated by adding the frequency of "Likes burritos" in the table)
To assess the association, we compare the ratio of the joint frequency to the product of the marginal frequencies:
Ratio = Joint frequency / (Marginal frequency of "Likes hamburgers" x Marginal frequency of "Likes burritos")
Ratio = 29 / (110 x 70)
Ratio ≈ 0.037 (rounded to three decimal places)
What is the distance between these set of points?
(1,-2), and (4,2)
sorry i cant add the photo of the graph but whoever the first one is to get it right will get brainliest
Answers
Hope this helps!
Answer:
go to khan academy on you tube he's really good at explaining stuff also sorry that's all i got...
Step-by-step e
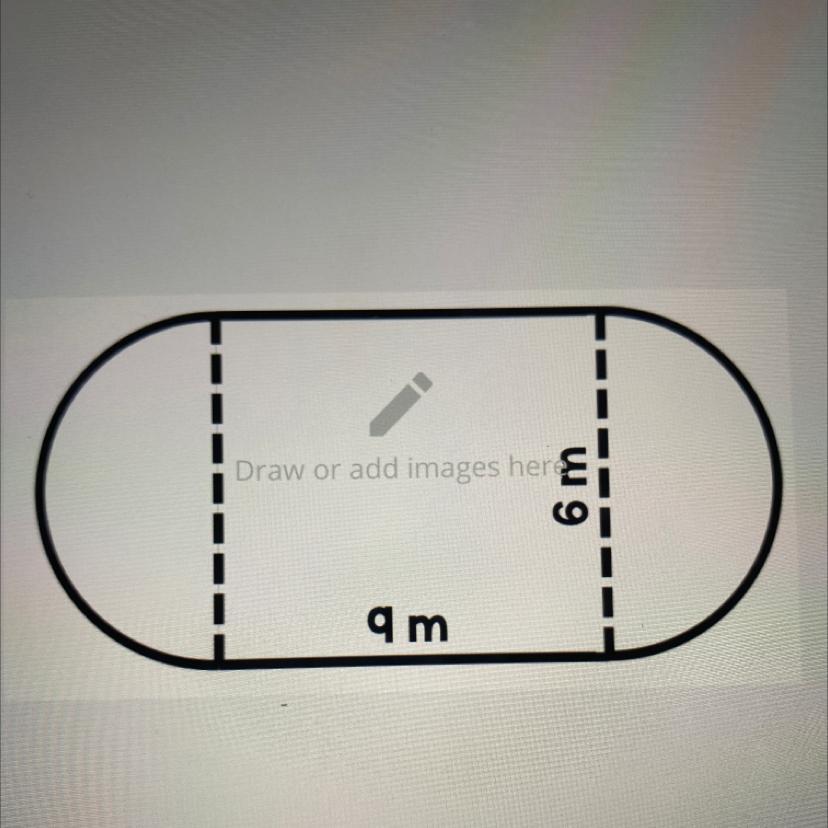
Find the area of the figure below. Round to the nearest tenth.
Answers
Which is the graph of the linear inequalityx2y>-6?
Answers
Answer:
We will graph the inequality in simplified form i.e \(y>-3\)
The graph is shown in figure below
Step-by-step explanation:
Which is the graph of the linear inequality \(2y>-6\)
(Note: Considering the inequality is 2y>-6 and x is typing mistake.)
First we will solve the inequality to find value of y
We have inequality:
\(2y>-6\)
For finding y we have to divide both sides of inequality by 2
\(\frac{2y}{2}>\frac{-6}{2} \\y>-3\)
Now, we will graph the inequality in simplified form i.e \(y>-3\)
Inequality can be graphed on number line as well as graph paper.
Graph on number line
Since y is greater than -3, so all values greater than -3 will be included on the number line. An open circle will be drawn on -3, indicating -3 is not included but values greater than -3 are included. The figure A shows the graph
Graph on Graph paper
Since y is greater than -3, so all values greater than -3 will be included on the number line. A dotted line will appear on -3 and the region on right side of -3 (values greater than 3) will be shaded. The figure B shows the graph


If f (x)
6x – 6 , find f (-1)
Answers
Answer:
-12
Step-by-step explanation:
f (x)=6x – 6
Let x= -1
f(-1) = 6(-1) -6
= -6-6
= -12
Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.
I ABSOLUTELY NEED HELP BY TOMORROW!!! I AM GIVING 100 POINTS

Answers
3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
How to Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.To express 3 1/2 cups as a multiplication expression using the unit "1 cup" as a factor, you can write it as:
3 1/2 cups = (3 + 1/2) cups = 3 cups + 1/2 cup
Since there are 1 cup in each term, we can rewrite it as:
3 cups + (1/2) cup
Now, we can express each term as a multiplication expression:
3 cups = 3 * 1 cup = 3
(1/2) cup = (1/2) * 1 cup = 1/2
Putting it all together, the multiplication expression is:
3 * 1 cup + (1/2) * 1 cup = 3 + 1/2
Therefore, 3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
Learn more about expression at https://brainly.com/question/1859113
#SPJ1
The diameters of bolts produced in a machine shop are normally distributed with a mean of 5.48 millimeters and a standard deviation of 0.07 millimeters. Find the two diameters that separate the top 3% and the bottom 3%. These diameters could serve as limits used to identify which bolts should be rejected. Round your answer to the nearest hundredth, if necessary.
Answers
The two diameters that separate the top 35 from the bottom 35 in the normal distribution are 5.35 mm and 5.61 mm .
Normal distributions are crucial to statistics because they are widely used in the natural and social sciences to represent real-valued covariates whose distributions are unknown.
Some of their significance comes from the main limit theorem. This claim states that, in some cases, the average of many samples (observations) of a stochastic process with limited mean and variance constitutes itself as a random variable, whose distribution tends to become more normal as the number of samples increases. Because of this, the distributions of physical quantities, like misspecification, which are thought to be the consequence of hundreds of distinct processes, are frequently close to normal.First we will find the bottom 3% such that P(X ≤ x) = 0.03
⇒ \(P(\frac{X-5.48}{0.07}\leq \frac{x-5.48}{0.07} )=0.03\)
⇒\(P(Z\leq \frac{x-5.48}{0.07} )=0.03\)
Now we will use the normal table to calculate the corresponding z-score.
\(\frac{x-5.48}{0.07} =-1.88\\\\\implies x = 5.348\)
Now we will find the same for the top part of the distribution.
\(P(\frac{X-5.48}{0.07}\leq \frac{x-5.48}{0.07} )=0.97\\\\\implies P(Z\leq \frac{x-5.48}{0.07} )=0.97\)
Now we will use the normal table to calculate the corresponding z-score.
\(\frac{x-5.48}{0.07} =1.88\\\\\implies x = 5.612\)
The two diameters that separate the top 35 from the bottom 35 in the normal distribution are 5.35 mm and 5.61 mm .
To learn more about normal distribution visit:
https://brainly.com/question/14916937
#SPJ1
t hits the square dartboard shown below at a random point. Find the probability that the dart lands in the shaded circular region. Each side of the dartbozn, and the radius of the shaded region Is 2 in.the value 3.14 for T. Round your answer to the nearest hundredth.

Answers
Given:
Required:
To find the probability that the dart land will be in the shaded region.
Explanation:
Area of the circle is given by the formula:
\(A=\pi r^2\)Where r = radius
Thus the area of the circular region
\(\begin{gathered} =(3.14)\times(2)^2 \\ =3.14\times4 \\ =12.56\text{ square in.} \end{gathered}\)The area of the square is given by the formula:
\(=(side)^2\)Thus the area of the given square
\(\begin{gathered} =(6)^2 \\ =36\text{ square in.} \end{gathered}\)The probability of an event is given by the formula:
\(P=\frac{number\text{ of possible outcomes}}{Total\text{ number of outcomes}}\)The probability that the dart land will be in the shaded region
\(=\frac{Area\text{ of the shaded region}}{Area\text{ of the square}}\)Thus probability
\(\begin{gathered} P=\frac{12.56}{36} \\ P=0.3488 \\ P=0.349 \end{gathered}\)Final answer:
Thus the probability that the dart land will be in the shaded region is 0.349.
