a 50-year-old athlete with a resting heart rate of 60 beats/min is training at 70% of his maximal heart rate. using the maximal heart rate method, what is his exercise heart rate?
Answers
The exercise heart rate of the 50-year-old athlete can be calculated using the maximal heart rate method. The maximal heart rate is estimated by subtracting the person's age from 220.
To calculate the exercise heart rate using the maximal heart rate method, we first need to determine the maximal heart rate. This can be estimated by subtracting the person's age from 220. In this case, the athlete is 50 years old, so the maximal heart rate would be 220 - 50 = 170 beats per minute.
Next, we need to find the exercise heart rate at 70% of the maximal heart rate. This can be done by multiplying the maximal heart rate by 0.7.
Therefore, the exercise heart rate for the 50-year-old athlete training at 70% of his maximal heart rate is 119 beats per minute. This means that during his training, his heart should be beating at approximately 119 beats per minute.
In summary, the main answer is that the exercise heart rate for the 50-year-old athlete is 119 beats per minute when training at 70% of his maximal heart rate.
Learn more about maximal heart rate method: https://brainly.com/question/1575299
#SPJ11
Related Questions
if you could get the answer with a short explanation that would be great!

Answers
Answer:
3x+1 is the correct answer

Answer:
3x + 1
Step-by-step explanation:
3x + 1
x - 5 I 3x² - 14x - 5 3x²÷x = 3x; (x-5)*3x = 3x² - 15x
3x² - 15x Subtract
- +
0 + x - 5 x ÷x = 1 ; (x -5)*1 = x - 5
x - 5 Subtract
- +
0
Mr. Smith is 81 years older than his grandson, Victor. In 3 years, Mr. Smith will be four times as old as Victor. How old is Victor now?
A) 21 years old
B) 22 years old
C) 24 years old
D) 27 years old
Answers
After 3 years 4(x+3)= x+81+3
4x+12= x +84
4x-x= 84–12= 72
3x = 72. Or x = 24
Now Victor's age is 24 and Mr. Smith is 105
In three years Victor will be 27and Mr. Smith will be 108 (four times of 27)
Using the chart, find the equation from the relation.

Answers
Answer:
-4
Step-by-step explanation:
y = x +b
6= 10 + b
b = 6 - 10
b = -4
Determine the equation of a line that passes through the point (3,-2) and is PERPENDICULAR to the equation
y= 3x - 1
Answers
If the line is perpendicular, it means the slope is negative reciprocal of 3, which is -1/3.
Equation where b (y-intercept) is unknown:
y= -1/3x + b
Replace x with 3 and y with -2 since the line passes through those points.
-2= -1/3(3) + b
-2= -3 + b
Add 3 to both sides of the equation:
1=b, the y-intercept is 1.
The full equation:
y = -1/3x + 1
Down Below: Question
Please help (50 BRAINLIST!!!!!!!!!!!)

Answers
The inequalities that represent the constraints in this situation are r+c≥80 and 1.45R +0.75c≤200 respectively
How to determine the inequalities?The amount with victor = $200
Let the number of roses purchased by Victor be R,
Also, Rose cost $1.45 each
Therefore cost of rose = 1.45R
A;so, let the number of carby Victor be C at a cost of $0.65 each nation purchased by victor be $0.65 each
Therefore, cost of carnation = $0.65c
1) The inequality to represent the constraint that every person takes home at least one rose is r+c≥80 and
2) the inequality to represent the cost constraint is 1.45R + 0.65≤200
Learn more about inequalities on https://brainly.com/question/30231190
#SPJ1
HELP FAST SECOND TIME POSTING❗️❗️❗️❗️The points (-1, r) and (5, -5) lie on a line with slope - 3. Find the missing coordinate r.
Answers
What is the weight of the seawater in an aquarium that is 4.4 ft long, 2.5 ft wide, and 5.3 ft high?
Answers
Answer:
The weight of the sea water in the aquarium is 3827.119 lb
Step-by-step explanation:
We start by calculating the volume of the aquarium
Since it is a cuboid, the volume will be L * B * H
= 4.4 * 2.5 * 5.3 = 58.3 ft^3
Mathematically;
Mass = density * volume
The density of sea water is 63.93 lb/ft^3
Mass = 63,93 * 58.3 = 3,827.119 lb
what is the probability that after a fair coin is tossed 5 times that the result will contain 3 'heads' given that the first toss was a 'head' ?
Answers
Using Conditional probability,
The probability that after a fair coin is tossed 5 times that the result will contain 3 'heads' given that the first toss was a 'head' is 3/5.
A fair coin is tossed five times .
so, total possible outcomes = 2⁵ = 32
Let A: head observed on first toss
B: 3 heads observed.
Probability that the first toss was head (p) = 1/2
we have to find out probability that on 5 tosses result contain 3 heads given that first toss wss head .
Using Binomial Probability distribution
P (X= x) = ⁿCₓ (p)ˣ (q)⁽ⁿ⁻ˣ⁾
x = 3 , n = 5
we get , P(B) = P(X= 3 ) = ⁵C₃(1/2)³(1/2)²
=> P(B) = 10 ×(1/2)⁵= 5/16
since the first toss is fixed as a head.
P(A ∩ B) =P( X₁ = 1 and X₂+ X₃ + X₄ + X₅) = P(X₁= 1)P(X₂+X₃+X₄+X₅)
= 1/2 × ⁴C₂ (1/2)⁵ = 3 (1/2)⁴
The required probability is , Conditional probability P(B/A) = P(A ∩ B)/P(A)
= 3(1/2)⁴/ 5/16 = 3/5
Hence , the required probability is 3/5.
To learn more about Conditional Probability, refer:
https://brainly.com/question/10567654
#SPJ4
What are the correct trigonometric ratios that could be used to determine the length of LN? Check all that apply. sin(20°) = L N Over 8 cos(70°) = 8 Over L N tan(70°) = L N Over M N sin(20°) = 8 Over L N cos(70°) = L N Over 8

Answers
Answer:
Sin(20)=LN/8
Cos(70)=LN/8
Step-by-step explanation:
The correct trigonometric ratios that could be used to determine the length of LN are sin20° =LN/8 and cos70° =LN/80. Therefore, option A and E are the correct answer.
What are trigonometric ratios?The sides and angles of a right-angled triangle are dealt with in Trigonometry. The ratios of acute angles are called trigonometric ratios of angles. The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec).
In the triangle LMN, ∠L=70°, ∠M=20° and LM= 8 units.
We know that sinθ= Opposite/Hypotenuse and cosθ=Adjacent/Hypotenuse
Here, sin20° =LN/8 and cos70° =LN/80
Therefore, option A and E are the correct answer.
Learn more about the trigonometric ratios here:
brainly.com/question/25122825.
#SPJ2
An object's velocity is given by v(t) = 0.5(t + 3)(t - 1)(t - 5)2, where t is time, in seconds. What is the total distance traveled by the object in the first 5 minutes? O 37.500 0 41.667 O 77.800 59.733
Answers
Therefore, The total distance traveled by the object in the first 5 minutes is approximately 59.733 units.
Explanation: To find the total distance traveled, we need to integrate the absolute value of the velocity function from t=0 to t=300 (5 minutes in seconds). Since the velocity function changes signs at t=-3, t=1, and t=5, we need to break up the integral into three parts: from 0 to -3, -3 to 1, and 1 to 5. After integrating and summing up the absolute values, we get a total distance of approximately 59.733 units.
Step 1: Calculate the integral of |v(t)| over [0, 300].
Step 2: Evaluate the integral and find the numerical value.
Integrate |0.5(t + 3)(t - 1)(t - 5)^2| from t = 0 to t = 300. Evaluate the integral to find the total distance traveled.
Therefore, The total distance traveled by the object in the first 5 minutes is approximately 59.733 units.
To know more about the function visit :
https://brainly.com/question/11624077
#SPJ11
? Question
Using the single taxable income tax brackets for 2018, select the appropriate marginal tax rate for each individual.
Select the correct rates in the table.
Individual
teacher, taxable income $40,259
pediatrician, taxable income $194,680
mathematician, taxable income $93,810
registered nurse, taxable income $55,350
Question 2
Tax Bracket
10% 12%
22%
32%
37%
35%
32% 24% 22%
22%
24% 32%
Answers
The appropriate marginal tax rates for each individual based on their taxable income are: Teacher - 12%, Pediatrician - 35%, Mathematician - 24%, Registered Nurse - 22%.
1: Using the single taxable income tax brackets for 2018, select the appropriate marginal tax rate for each individual. Select the correct rates in the table. Individual Taxable Income Marginal Tax Rate Teacher $40,259 12% Pediatrician $194,680 35% Mathematician $93,810 24% Registered Nurse $55,350 22%
2: Tax Bracket 10% 12% 22% 24% 32% 35% 37% The given table shows the marginal tax rates for single taxable income tax brackets in the year 2018. The marginal tax rate refers to the tax rate that applies to the next additional dollar of income. It is essential to know the marginal tax rate for the calculation of the tax bill. Now, we have to select the appropriate marginal tax rate for each individual.
Teacher -Taxable Income = $40,259. The appropriate marginal tax rate for the teacher is 12%. The income of the teacher falls in the taxable income bracket of $38,701 to $82,500, and the marginal tax rate is 12%.
Pediatrician - Taxable Income = $194,680. The appropriate marginal tax rate for the pediatrician is 35%. The income of the pediatrician falls in the taxable income bracket of $157,501 to $200,000, and the marginal tax rate is 35%.
Mathematician - Taxable Income = $93,810. The appropriate marginal tax rate for the mathematician is 24%. The income of the mathematician falls in the taxable income bracket of $82,501 to $157,500, and the marginal tax rate is 24%.
Registered Nurse - Taxable Income = $55,350. The appropriate marginal tax rate for the registered nurse is 22%. The income of the registered nurse falls in the taxable income bracket of $38,701 to $82,500, and the marginal tax rate is 22%.
Thus, the appropriate marginal tax rate for each individual is as follows: Individual Taxable Income Marginal Tax Rate Teacher $40,259 12% Pediatrician $194,680 35% Mathematician $93,810 24% Registered Nurse $55,350 22%In summary, the marginal tax rate refers to the tax rate that applies to the next additional dollar of income. It is essential to know the marginal tax rate for the calculation of the tax bill. The appropriate marginal tax rate for each individual depends on their taxable income and taxable income bracket. The given table shows the marginal tax rates for single taxable income tax brackets in the year 2018.
For more questions on tax rates
https://brainly.com/question/30892092
#SPJ8
The measure of 2A is 18° greater than the measure of 2B. The two angles are complementary. Find
the measure of each angle.
The MzA is
and mzB is
lo
Answers
Answer:
2A=54°
2B=36°
Step-by-step explanation:
2A=x+18
2B=x
x+x+18=90
2x=90=18
2x=72
x=36
2A=x+18=36+18=54
2B=x=36
10 The bottom of a 15-ft ladder is placed 12 ft from a wall. How far above the ground does the top of the ladder touch the wall? Show your work.
Answers
The top of the ladder touches the wall at 9 ft above the ground.
We are given that;
Measurements= 15ft and 12ft
Now,
To find the height of the ladder on the wall, we can use the Pythagorean theorem. The ladder, the wall, and the ground form a right triangle, where the ladder is the hypotenuse and the wall and the ground are the legs. The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the legs. Using this theorem, we get:
h^2 + 12^2 = 15^2 h^2 + 144 = 225 h^2 =225 - 144 h^2= 81 h=sqrt(81) h= 9
Therefore, by the Pythagoras theorem the answer will be 9 ft
Learn more about Pythagoras theorem;
https://brainly.com/question/343682
#SPJ1
Can anyone help me with this question please

Answers
Step-by-step explanation:
all the functions with the "exponent" -1 mean inverse function (and not 1/function).
the inverse function gets a y value as input and delivers the corresponding x value as result.
so,
\(g { }^{ - 1} (0)\)
gets 0 as input y value. now, what was the x value in g(x) that delivered 0 ?
4
that x value delivering 0 as y was 4.
so,
\(g {}^{ - 1} (0) = 4\)
the inverse function for a general, continuous function get get by transforming the original functional equation, so that x is calculated out of y :
h(x) = y = 4x + 13
y - 13 = 4x
x = (y - 13)/4
and now we rename x to y and y to x to make this a "normal" function :
y = (x - 13)/4
so,
\(h {}^{ - 1} (x) = (x - 13) \div 4\)
a combined function (f○g)(x) means that we first calculate g(x) and then use that result as input value for f(x). and that result is then the final result.
formally, we simply use the functional expression of g(x) and put it into every occurrence of x in f(x).
so, we have here
4x + 13
that we use in the inverse function
((4x + 13) - 13)/4 = (4x + 13 - 13)/4 = 4x/4 = x
the combination of a function with its inverse function always delivers the input value x unchanged.
so,
(inverse function ○ function) (-3) = -3
Answer:
\(\text{g}^{-1}(0) =\boxed{4}\)
\(h^{-1}(x)=\boxed{\dfrac{x-13}{4}}\)
\(\left(h^{-1} \circ h\right)(-3)=\boxed{-3}\)
Step-by-step explanation:
The inverse of a one-to-one function is obtained by reflecting the original function across the line y = x, which swaps the input and output values of the function. Therefore, (x, y) → (y, x).
Given the one-to-one function g is defined as:
\(\text{g}=\left\{(-7,-3),(0,2),(1,3),(4,0),(8,7)\right\}\)
Then, the inverse of g is defined as:
\(\text{g}^{-1}=\left\{((-3,-7),(2,0),(3,1),(0,4),(7,8)\right\}\)
Therefore, g⁻¹(0) = 4.
\(\hrulefill\)
To find the inverse of function h(x) = 4x + 13, begin by replacing h(x) with y:
\(y=4x+13\)
Swap x and y:
\(x=4y+13\)
Rearrange to isolate y:
\(\begin{aligned}x&=4y+13\\\\x-13&=4y+13-13\\\\x-13&=4y\\\\4y&=x-13\\\\\dfrac{4y}{4}&=\dfrac{x-13}{4}\\\\y&=\dfrac{x-13}{4}\end{aligned}\)
Replace y with h⁻¹(x):
\(\boxed{h^{-1}(x)=\dfrac{x-13}{4}}\)
\(\hrulefill\)
As h and h⁻¹ are true inverse functions of each other, the composite function (h o h⁻¹)(x) will always yield x. Therefore, (h o h⁻¹)(-3) = -3.
To prove this algebraically, calculate the original function of h at the input value x = -3, and then evaluate the inverse of function h at the result.
\(\begin{aligned}\left(h^{-1}\circ h \right)(-3)&=h^{-1}\left[h(-3)\right]\\\\&=h^{-1}\left[4(-3)+13\right]\\\\&=h^{-1}\left[1\right]\\\\&=\dfrac{1-13}{4}\\\\&=\dfrac{-12}{4}\\\\&=-3\end{aligned}\)
Hence proving that (h⁻¹ o h)(-3) = -3.
please help me with this

Answers
Answer:
5 squared, 2 and half, 7 squared, 11 squared, pie
Step-by-step explanation:
if you select two pets from the store randomly, what is the probability that they are both the same species?
Answers
The probability that the two pets selected are of the same species is 0.2426 .
In the question ,
it is given that ,
the number of puppies in the pet store = 6
the number of kittens in the pet store = 9
the number of lizards in the pet store = 4
the number of snakes in the pet store = 5
total animals = 24
the probability of selecting 2 puppies = ⁶C₂/²⁴C₂
the probability of selecting 2 kittens = ⁹C₂/²⁴C₂
the probability of selecting 2 lizards = ⁴C₂/²⁴C₂
the probability of selecting 2 snakes = ⁵C₂/²⁴C₂
So , the required probability is
= ⁶C₂/²⁴C₂ + ⁹C₂/²⁴C₂ + ⁴C₂/²⁴C₂ + ⁵C₂/²⁴C₂
Simplifying further ,
we get ,
= 5/92 + 3/23 + 1/46 + 5/138
= 0.0543 + 0.1304 + 0.0217 + 0.0362
= 0.2426
Therefore , the required probability is 0.2426 .
The given question is incomplete , the complete question is
The pet store has 6 puppies , 9 kittens , 4 lizards and 5 snakes . if you select two pets from the store randomly, what is the probability that they are both the same species ?
Learn more about Probability here
https://brainly.com/question/14570375
#SPJ4
Which value cannot represent the probability of an event occurring? StartFraction 1 over 100 EndFraction 0. 29 85% Three-half.
Answers
Answer:
29
Step-by-step explanation:
The probability of an event happening is a number from 0 (even will cannot possibly happen) to 1 (event will definitely happen.)
0 ≤ p ≤ 1
1/100, 0, 85% are all numbers from 0 to 1.
29 is not from zero to 1, so the answer is 29.
Every value{0.01, 0.29, 85%} can represent the probability of an event occurring except option d that is 1.5.
Given to us,
a.) \(\dfrac{1}{100}\)
b.) 0.29
c.) 85%
d.) \(\dfrac{3}{2}\)
The probability help us to know about the probability of specific events occurring.
For a sure event, the probability is always 1,
while for an event that will never happen the probability is always 0.
Thus, probability(p), \(\bold{1 \geq p\geq 0}\).
Now looking at the options,
a.) \(\dfrac{1}{100}\) = 0.01
b.) 0.29
c.) 85% = 0.85
d.) \(\dfrac{3}{2}\) = 1.5
Now comparing each option with \(\bold{1 \geq p\geq 0}\).
Therefore, the only option which is not feasible is option d that is 1.5.
Hence, every value{0.01, 0.29, 85%} can represent the probability of an event occurring except option d that is 1.5.
To know more visit:
https://brainly.com/question/795909
What is theoretical probability of pulling a green marble out of the bag?

Answers
What is the approximate circumference of the circle shown below

Answers
Answer: A) 46.5 cm
Step-by-step explanation:
Circumference = 2 π r or Circumference = π d
In this case, they give us the diameter = 14.8 cm. Therefore the radius = 14.8/2 = 7.4 cm.
π ≈ 3.14.
We can use either equation above, but because the diameter was given, we will use c = πd for simplicity.
C = π d
= (3.14)(14.8)
= 46.47 cm, which rounds to 46.5 cm
For what value of A is x 5 a factor of x² 3x² ax 10?
Answers
The value of A when x - 5 is a factor of x³ - 3x² + ax - 10 is -8.
A polynomial factor is a polynomial that divides another polynomial exactly, with no remainder.
For example, if we have a polynomial P(x) = x³ - 3x² + ax - 10, and we have a polynomial factor F(x) = x - 5, we can say that P(x) is divisible by F(x) with no remainder.
In general, a polynomial of degree n has n roots (or zeroes) and the factorization of polynomial can be expressed as a product of its roots and its corresponding multiplicity.
To find the value of A, set x = 5 in the equation x³ - 3x² + ax - 10 and solve for A that will make the equation equal to zero..
So when x = 5, we have:
x³ - 3x² + ax - 10 = 0
(5)³ - 3(5)² + a(5) - 10 = 0
125 - 75 + 5a - 10 = 0
5a = -40
a = -8
Hence, if x - 5 is a factor of x³ - 3x² + ax - 10, then A is equal to -8.
Learn more about polynomial factor here: brainly.com/question/30090287
#SPJ4
TRIANGLE CONGRUENCE! PICTURE ADDED. How is QTP congruent to SPT?

Answers
Answer:
The triangles are congruent because:
QP = STangle P = angle Tthe side PT is in both trianglesWe know when 2 sides of two triangles and the angle between them is congruent, the triangles are congruent.
Find m∠IUV if m∠IUV=x+49, m∠TUI=x+63, and m∠TUV=106∘.?
I'll mark you brainliest!
Answers
Answer:
46
Step-by-step explanation:
You have to do IVU+TUI=TUV
so... x+49+x+63=106
The doctor tells the patient to cut back on coffee. the patient usually has four 8-oz cups of coffee per day. if the doctor told him to cut back by 25%, how many ounces of coffee can the patient have each day? (enter numeric value only. if rounding is necessary, round to the whole number.)
Answers
The ounces of coffee the patient have each day is 24 oz.
What is reduction of percentage?A difference among starting and final numbers is the percentage drop. It displays a percentage loss of value compared to the original regardless of the units. The difference between the initial and final amounts is the amount of decline.
Some characteristics of percentage change are-
Any amount that is measured over time can be changed as a percentage.The percentage difference between a value and its starting point is known as a percentage decline.A percentage decline indicates a reduction in value from the starting quantity.Calculation for the coffee that the patient consume each day,
Determination for the coffee he consumes daily.
4 cups x 8 oz = 32 oz
Now, multiply the outcome by the decimal equivalent of the percentage (i.e., 25% = 25/100).
32 x (25/100) = 8
Finally, remove the percentage from the weekly coffee consumption.
32-8 = 24 oz per day
Therefore, the consumption of the coffee by the patient reduced to 24 oz per day from 32 oz per day.
To know more about percentage reduction, here
https://brainly.com/question/20758765
#SPJ4
A forward start option will, in 6 months, give its owner a European put option expiring year later with a strike price equal to the stock price at the end of 6 months You are given (s) The European put option is on a stock that pays no dividends. (b) The stock volatility is 30% (e) The current price of the stock is 40. (d) The continuously compounded risk-free interest rate is 8%. Under the Black Scholes framework, determine the price of the forward start option
Answers
The price of the forward start option is approximately -2.74
To determine the price of the forward start option, we can use the Black-Scholes formula for European options. However, since the forward start option becomes active in 6 months, we need to adjust the formula accordingly.
The Black-Scholes formula for a European put option is as follows:
P = S * N(-d1) - X * e^(-rT) * N(-d2)
where:
P = Price of the put option
S = Current price of the stock
N() = Cumulative standard normal distribution function
d1 = (ln(S/X) + (r + σ^2/2) * T) / (σ * sqrt(T))
d2 = d1 - σ * sqrt(T)
X = Strike price of the option
r = Risk-free interest rate
T = Time to expiration in years
σ = Stock volatility
In this case, since the forward start option becomes active in 6 months, the time to expiration T will be 1 year - 6 months = 0.5 years.
Let's calculate the price of the forward start option:
S = 40 (given)
X = S (strike price equal to the stock price at the end of 6 months)
r = 8% = 0.08 (given)
T = 0.5 (6 months)
σ = 30% = 0.3 (given)
First, we calculate d1 and d2:
d1 = (ln(40/40) + (0.08 + 0.3^2/2) * 0.5) / (0.3 * sqrt(0.5))
= (0 + (0.08 + 0.09) * 0.5) / (0.3 * sqrt(0.5))
= (0.17 * 0.5) / (0.3 * 0.7071)
≈ 0.2833
d2 = 0.2833 - 0.3 * sqrt(0.5)
≈ 0.2833 - 0.3 * 0.7071
≈ 0.2833 - 0.2121
≈ 0.0712
Now, we can calculate the price of the forward start option using the Black-Scholes formula:
P = 40 * N(-0.2833) - 40 * e^(-0.08 * 0.5) * N(-0.0712)
Using a standard normal distribution table or a calculator that provides the cumulative standard normal distribution function (N()), we find:
N(-0.2833) ≈ 0.3895
N(-0.0712) ≈ 0.4684
P = 40 * 0.3895 - 40 * e^(-0.08 * 0.5) * 0.4684
Using the given values and performing the calculation:
P ≈ 15.58 - 40 * e^(-0.04) * 0.4684
≈ 15.58 - 40 * 0.9802 * 0.4684
≈ 15.58 - 18.32
≈ -2.74
Therefore, the price of the forward start option is approximately -2.74
Learn more about forward start option here:
https://brainly.com/question/32722506
#SPJ11
Solve for height using the tangent method. Show your work.
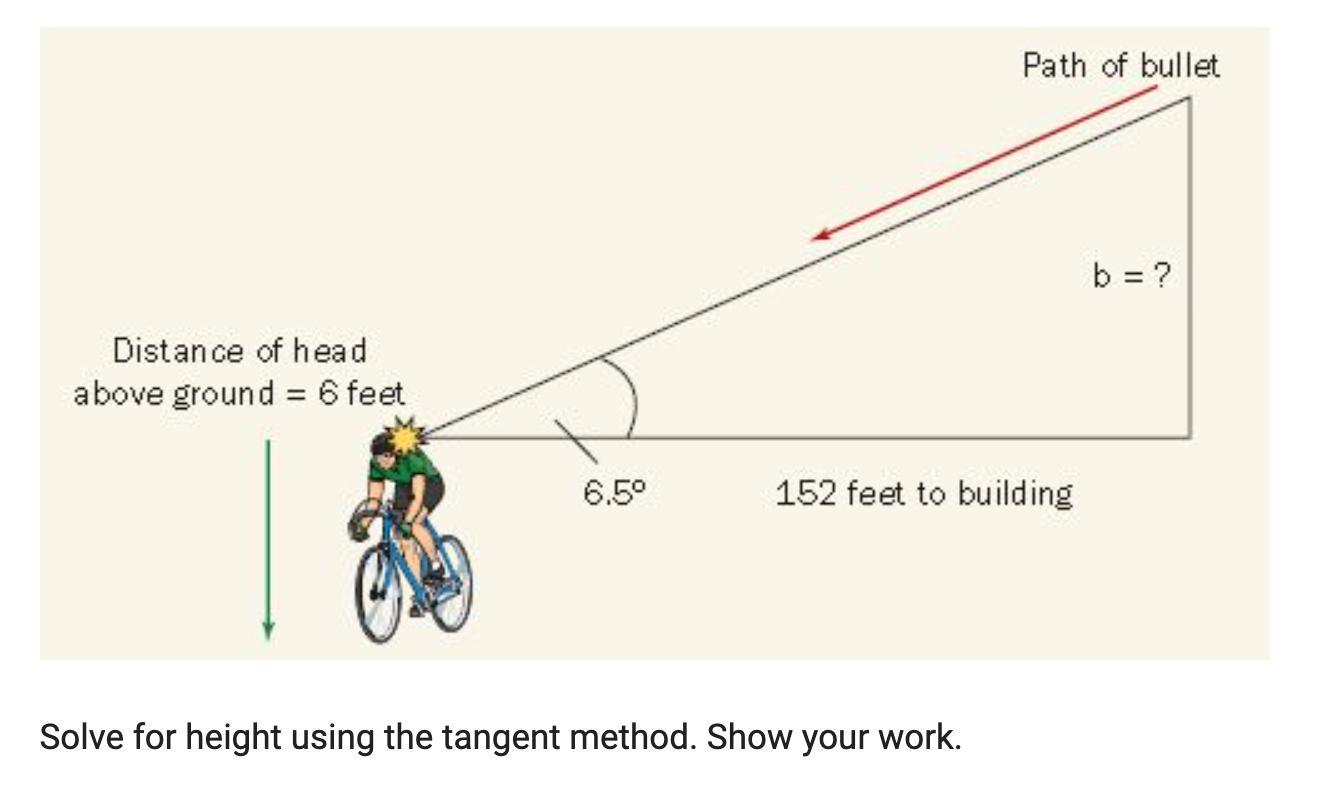
Answers
Answer:
b = 17.318 height = 23.318 ft
Step-by-step explanation:
This IS very similar to the other one, Emily..... Have you tried to solve it the same way?
b = 152 tan 6.5 = 17.318 ft (using a calculator)
add the height of the victim's head (6 ft)
17.318 + 6 = 23.318 ft
I have been stuck on this problem for so long. PLEASE HELP!!!

Answers
The result of this calculation, -91/72, is a fraction in reduced form
THE SOLUTION FOR THE EQUATION IS AS FOLLOWS :-
To find C + (1/3)Y, we simply substitute the given values of C and Y into the expression and perform the necessary arithmetic.
C + (1/3)Y = (-8/9) + (1/3)(-3/8)
To add these fractions, we need a common denominator. The lowest common multiple of 9 and 8 is 72.
C + (1/3)Y = (-8/9)(8/8) + (1/3)(-3/8)(9/9)
C + (1/3)Y = (-64/72) + (-27/72)
C + (1/3)Y = -91/72
Therefore, C + (1/3)Y = -91/72.
In words, the expression C + (1/3)Y represents the sum of two values: C and one-third of Y. This can be thought of as a weighted sum, where C has a weight of 1 and Y has a weight of 1/3.
The result of this calculation, -91/72, is a fraction in reduced form. It is negative, which means that the sum of C and one-third of Y is less than zero.
It's important to note that while this calculation involves fractions and arithmetic operations, the concept of a weighted sum is used in many different areas of mathematics and science. In statistics, for example, a weighted sum is used to calculate the mean of a set of values, where each value has a different weight. In physics, a weighted sum is used to calculate the center of mass of an object, where each point on the object has a different weight.
To know more about mathematical operations visit:-
https://brainly.com/question/4721701
#SPJ1
What is the relation between 1 and 2?

Answers
Answer:
Supplementary and Linear Pair
Step-by-step explanation:
The angles 1 and 2 form 180 degrees. That is the definition of a Supplementary Angle and Linear Pair.
Find the missing values in the ratio table.

Answers
Answer:
ok i cant tell if the dot is a decimal or a spot, im thinking its just a spot
so the answer would be 8:2 4:1 2:0.5
Step-by-step explanation:
if it is a decimal
the first box would be 8:0.2
Point G is on line segment
F
H
‾
FH
. Given
G
H
=
8
,
GH=8,
F
H
=
3
x
+
3
,
FH=3x+3, and
F
G
=
2
x
,
FG=2x, determine the numerical length of
F
G
‾
.
FG
.
Answers
The numerical length of the line segment FG is 10 units.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables. An independent variable is a variable that does not depend on other variables while a dependent variable is a variable that depends on other variables.
Point G is on FH, hence:
FH = FG + GH
Given that GH = 8, FH = 3x + 3, FG = 2x, hence:
3x + 3 = (2x) + 8
x = 5
FG = 2x = 2(5) = 10
The numerical length of the line segment FG is 10 units.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
PLEASE HELP!!!
Which of the following is the Best Buy?
1 L for $1.68
0.5 L for $1.29
2 L for $3.40
3 L for $5.07
Answers
Answer:
it's 1 L
Step-by-step explanation:
it's pretty easy just do some multiplication