A bag contains several balls. There are 8 red balls, 6 yellow balls, 7 green balls and 2purple balls. If you pull out one ball from the bag, the probability, as a percentage,that you get a red or purple ball is __%.Type your answer in the box provided. Round your answer to the nearest tenth of apercent.
Answers
8 red balls
6 yellow balls
7 green balls
2 purple balls
Total balls: 23
The probability of getting a red or a purple ball is:
P(red or purple) = P(red) + P(purple)
But:
P(red) = (# of red balls) / Total = 8/23
P(purple) = (# of purple balls) / Total = 2/23
Then:
P(red or purple) = 8/23 + 2/23 = 10/23 = 0.43478
In percentage form, to the nearest tenth: 43.5%
Related Questions
Find the domain and range of the exponential function h(x) = –343x.
Explain your findings.
As x decreases, does h increase or decrease? Explain.
As x increases, does h increase or decrease? Explain.
Answers
The function is supposed to be;
h(x) = -343^(x)
Answer:
The domain will be a set of real numbers while the range will be y ≤ 0 and on the interval (-∞, 1)
As x is increasing, h is decreasing and as x is decreasing, h is increasing
Step-by-step explanation:
We are given the function as;
h(x) = -343^(x)
The formula is;
y = a^(x) since it's symmetrical to the x-axis
However in this case;
y = -a^(x)
Now, the domain is y and the range is a set of values of x.
I've attached a graph of this function drawn on desmos.
From the graph we can see that The domain will be a set of real numbers while the range will be on the interval (-∞, 1)
For a value of x = 0,we have;
h(0) = -343^(0)
h(0) = -343
When we increase the value of x to 3,we have;
h(3) = -343^(3)
h(3) = -40353607
When we decrease the value of x to -3, we have;
h(-3) = -343^(-3)
h(-3) = 0.00000002478
Thus, we can conclude that;
As x is increasing, h is decreasing and as x is decreasing, h is increasing

Write a recursive formula for an, the nth term of the sequence 50, -10, 2, ....
a1
an
11
Answers
Answer:do homework
Step-by-step explanation:
The area of a triangle is 24 square inches. What is the height of the triangle if the base length is 4 inches? (5 points) 6 inches 8 inches 12 inches 20 inches
Answers
9514 1404 393
Answer:
12 inches
Step-by-step explanation:
The area is given by the formula ...
A = 1/2bh
Fill in the given values and solve for the height.
24 in² = 1/2(4 in)h
h = (24 in²)/(2 in) = 12 in
The height of the triangle is 12 inches.
Answer:
12 inches
Step-by-step explanation:
Area = \(\frac{1}{2}bh\)
24 = \(\frac{1}{2} * 4 * h\)
24 = 2h
h = 12 inches
What graph represents the following piecewise defined function?
g(x)={x^2, x<0, 1/2x, 0 4
Answers
Answer:
option 2
Step-by-step explanation:
The graph represents the following piecewise defined function is attached below.
What is a function?A function is an expression that illustrates the connection between two or more variables and numbers. A function defined by several subfunctions, each of which is applicable to a distinct interval in the domain, is said to be piecewise.
We have a function,
g(x) = { x², x<0
1/2 x , 0<x<4
A function defined by several subfunctions, each of which is applicable to a distinct interval in the domain, is said to be piecewise.
The below-attached piecewise function is available.
Given the following piecewise function, the graph is attached below.
Learn more about piecewise function here: brainly.com/question/10733545
#SPJ5

2 A motorist drove 162 miles in 3 hours. At that rate, how many miles would the motorist travel in a half hour? F 81 mi G 324 mi H 27 mi J 54 mi
can someone please help me ?
Answers
Answer:
i really dont know
Step-by-step explanation:
i really dont know
Answer:
27
Step-by-step explanation:
162 divide by 3 = 54 divided by 2 =27 I think this is the answer
a triangle has angles that measure 50 degrees and 50 degrees what is the measure lf the third angle?
Answers
Answer:
80
Step-by-step explanation:
the combined angles of any triangle equal 180 degrees. take the known angles ( 50 and 50) and subtract their sum from 180. 180-100=80
6=a/4+2. This is a two step equation
Answers
Answer:
Step-by-step explanation:
6 = a / 4 + 2
=> 6 - 2 = a / 4 + 2 - 2
=> 4 = a / 4
=> a = 16
Answer:
a = 16
Step-by-step explanation:
\(6=a/4+2\)
\(6(-2)=a/4+2(-2)\)
\(4=a/4\)
\(4(4)=(a/4)(4)\)
\(16=a\)
\(a=16\)
f(4) =
If g(x) = 2, x=
PLEASEE HELP!

Answers
Answer:
f(4) = -10
If g(x) = 2, x = 0
Step-by-step explanation:
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
Answers
Answer:
53\(x_{123}\) == 134 cf
Step-by-step explanation:
A - on the po boyds at a emase the foot, 1, of building. He. Observes an obje- et on the top, P of the building at an angle of ele- building of 66 Aviation of 66 Hemows directly backwards to new point C and observes the same object at an angle of elevation of 53° · 1P) |MT|= 50m point m Iame horizontal level I, a a
The height of the building is approximately 78.63 meters.
The following is a step-by-step explanation of how to solve the problem. We'll need to use some trigonometric concepts and formulas to find the solution.
Draw a diagram of the situation described in the problem to get a better understanding of the problem. The diagram would have a right-angled triangle with angle of elevation of 66° at the bottom left vertex and another angle of elevation of 53° at the bottom right vertex. The object on top of the building is at the vertex of the triangle. Point M and I on the diagram are points on the horizontal line of sight and on the ground respectively. We can label the diagram with the following values:Angle of elevation from point A = 66°Angle of elevation from point P = 53° Length of line segment AM = h Length of line segment MP = x Length of line segment IP = y Length of line segment MT = 50m. We'll use these values to calculate the length of h, which is the height of the building.Use the tangent ratio to find x:tan 66° = h / x => x = h / tan 66°. Use the tangent ratio to find y:tan 53° = h / y => y = h / tan 53°.We know that x + y = 50, so substituting the expressions for x and y from step 3 gives:h / tan 66° + h / tan 53° = 50h = 50 tan 66° tan 53° / (tan 53° + tan 66°) ≈ 78.63 m.Therefore, the height of the building is approximately 78.63 meters.
For more such questions on height, click on:
https://brainly.com/question/28122539
#SPJ8
A number cube is rolled. Event A is rolling an odd number, and event B is rolling a factor of 12. What is P(AU B)?
Answers
Explanation:
A = set of odd numbers = {1,3,5}
B = set of factors of 12 = {1,2,3,4,6}
A U B = union of set A and set B
A U B = {1,3,5} union {1,2,3,4,6}
A U B = {1,3,5, 1,2,3,4,6}
A U B = {1,2,3,4,5,6}
The set union operation combines two sets into one bigger set. Duplicates are tossed out.
There are 6 elements in the set A U B = {1,2,3,4,5,6} out of 6 faces of the number cube.
Therefore, the probability event A U B happens is 6/6 = 1 = 100%; i.e. it is guaranteed to happen. Each face of the number cube is either odd, a factor of 12, or both.
Side notes:
A U B can be read out as "event A or event B"; so P(A U B) is "the probability event A happens or B happens or both".A intersect B = {1,3} = values that are in both set A and set B at the same time. These are both odd and a factor of 12.answer with explanation please

Answers
Answer:
D. x>5
Step-by-step explanation:
\(3x + 2 < 4x - 3 \\ = 3x - 4x < - 3 - 2 \\ = - x < - 5 \\ = x > 5\)
The first number in a pattern is 84. The pattern follows the rule divide by 2 then add 10. Find the next three terms and then describe the pattern
Answers
Answer:
84
34
27
Step-by-step explanation:
WEEK 2 Direction: Answer the following problems. 1. Jun wanted to know how much ice cream he got in on scoop. The radius of a scoop is 2 inches. Find the volum Use 3.14 for pi. (SHOW YOUR SOLUTION) a) What is asked in the problem? b) What are the given facts? c) What is the formula to be used? d) Number Sentence e) Final answer. (show your solution pls)
Answers
We are given the radius of the scoop and asked to find the volume of ice cream in one scoop. By using the formula for the volume of a sphere and substituting the given radius, we can calculate the volume. The final answer is approximately 33.49 cubic inches.
a) The problem asks for the volume of ice cream in one scoop.
b) The given fact is that the radius of the scoop is 2 inches.
c) The formula to be used is the volume of a sphere, which is given by V = (4/3)πr³, where V is the volume and r is the radius.
d) Number Sentence:
- Given: Radius (r) = 2 inches
- Formula: V = (4/3)πr³
- Substituting the value: V = (4/3)π(2)³
- Simplifying: V = (4/3)π(8)
- Evaluating: V = (4/3)(3.14)(8)
- Multiplying: V = 33.49333333 (approx.)
e) Final answer: The volume of ice cream in one scoop is approximately 33.49 cubic inches.
For more such questions on volume
https://brainly.com/question/1972490
#SPJ8
answer the question submitted

Answers
The function g(x) = 4x² - 28x + 49 can be rewritten as g(x) = 4(x - 7/2)² - 147 after completing the square.
To complete the square for the function g(x) = 4x² - 28x + 49, we follow these steps:
Step 1: Divide the coefficient of x by 2 and square the result.
(Coefficient of x) / 2 = -28/2 = -14
(-14)² = 196
Step 2: Add and subtract the value obtained in Step 1 inside the parentheses.
g(x) = 4x² - 28x + 49
= 4x² - 28x + 196 - 196 + 49
Step 3: Rearrange the terms and factor the perfect square trinomial.
g(x) = (4x² - 28x + 196) - 196 + 49
= 4(x² - 7x + 49) - 147
= 4(x² - 7x + 49) - 147
Step 4: Write the perfect square trinomial as the square of a binomial.
g(x) = 4(x - 7/2)² - 147
Therefore, the function g(x) = 4x² - 28x + 49 can be rewritten as g(x) = 4(x - 7/2)² - 147 after completing the square.
For more such questions square,click on
https://brainly.com/question/27307830
#SPJ8
The probable question may be:
Rewrite the function by completing the square.
g(x)=4x²-28x +49
g(x)= ____ (x+___ )²+____.
Three middle schools in a city had enrollments of 296,315 and 278 what was the total middle school enrollment
Answers
The total middle school enrollment is 889 for the given city.
According to the question,
We have the following information:
Three middle schools in a city had enrollments of 296,315 and 278.
Now, the total middle school enrollment can be easily found by adding the enrollments in three middle schools of the city.
So, we have the following expression:
Total middle school enrollment = 296+315+278
(We already know that the digits are first added from the right hand side and then we move to the left hand side.)
Total middle school enrollment = 889
Hence, the total middle school enrollment is 889 for the given city.
To know more about middle school enrollment here
https://brainly.com/question/18836384
#SPJ9
PLEASE HELP WILL MARK BRAINLIEST
Two angles are supplementary. The measure of one angle
is 16 more than two times the measure of the other
angle. How many degrees are in each angle?

Answers
Answer:
The angles are 54 2/3 degrees and 115 1/3 degrees
Step-by-step explanation:
make an equation for the angles x being one angle and y being the other
16+ 2x =y
Supplementary angles add to 180
x + y = 180
Fill in y with the first equation
x + 16 +2x =180
simplify
3x +16 =180
subtract 16 from both sides
3x = 164
divide both sides by 3
x = 54 2/3
Insert the value of x into the first equation then simplify
16 + 2(54 2/3) =y
16 + 109 1/3 =y
115 1/3 =y
Solve for b, show your work
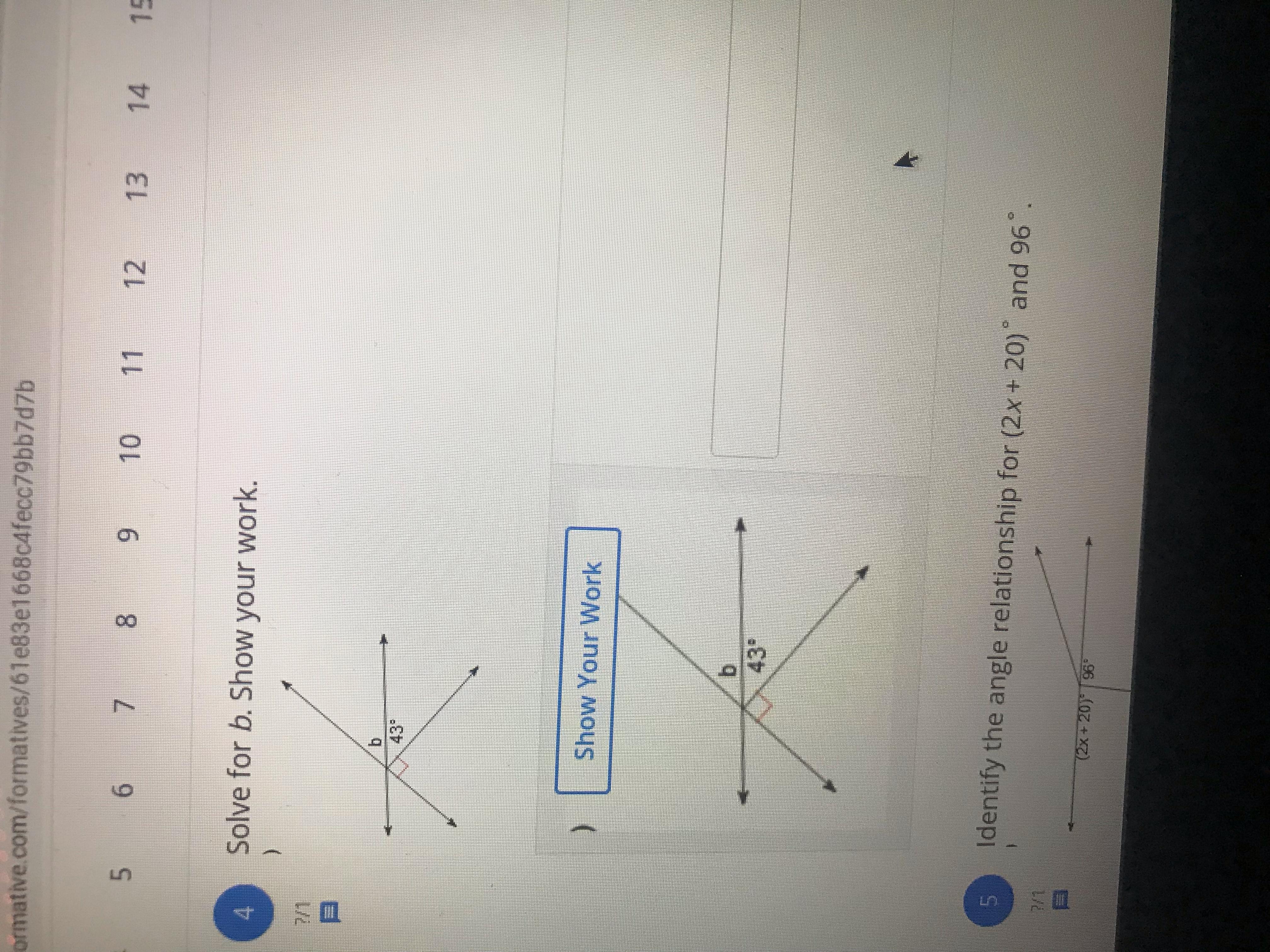
Answers
Answer:
b= 47
Step-by-step explanation:
180-90 =90
90 -43 =47
Answer:
b = 47°
Step-by-step explanation:
The 3 angles lie on a straight line and sum to 180° , that is
b + 43° + 90° = 180°
b + 133° = 180° ( subtract 133° from both sides )
b = 47°
8. How many terms are in the following expression? a + b + 3c²-2ab + 12a²ba. 2b.5c.3d. not enough information
Answers
√100 +4, √81 + A, √64 + 6, √49 + B, √36 +8, √25+ C
Answers
Answer:
Step-by-step explanation:
Simplifying square roots
Example
Let's simplify \sqrt{75}
75
square root of, 75, end square root by removing all perfect squares from inside the square root.
We start by factoring 757575, looking for a perfect square:
75=5\times5\times3=\blueD{5^2}\times375=5×5×3=5
2
×375, equals, 5, times, 5, times, 3, equals, start color #11accd, 5, squared, end color #11accd, times, 3.
We found one! This allows us to simplify the radical:
\begin{aligned} \sqrt{75}&=\sqrt{\blueD{5^2}\cdot3} \\\\ &=\sqrt{\blueD{5^2}} \cdot \sqrt{{3}} \\\\ &=5\cdot \sqrt{3} \end{aligned}
75
=
5
2
⋅3
=
5
2
⋅
3
=5⋅
3
So \sqrt{75}=5\sqrt{3}
75
=5
3
square root of, 75, end square root, equals, 5, square root of, 3, end square root.
Want another example like this? Check out this video.
Practice
PROBLEM 1.1
Simplify.
Remove all perfect squares from inside the square root.
{\sqrt[]{12}}=
12
=root, start index, end index, equals
Explain
Want to try more problems like these? Check out this exercise.
Simplifying square roots with variables
Example
Let's simplify \sqrt{54x^7}
54x
7
square root of, 54, x, start superscript, 7, end superscript, end square root by removing all perfect squares from inside the square root.
First, we factor 545454:
54=3\cdot 3\cdot 3\cdot 2=3^2\cdot 654=3⋅3⋅3⋅2=3
2
⋅654, equals, 3, dot, 3, dot, 3, dot, 2, equals, 3, squared, dot, 6
Then, we find the greatest perfect square in x^7x
7
x, start superscript, 7, end superscript:
x^7=\left(x^3\right)^2\cdot xx
7
=(x
3
)
2
⋅xx, start superscript, 7, end superscript, equals, left parenthesis, x, cubed, right parenthesis, squared, dot, x
And now we can simplify:
\begin{aligned} \sqrt{54x^7}&=\sqrt{3^2\cdot 6\cdot\left(x^3\right)^2\cdot x} \\\\ &=\sqrt{3^2}\cdot \sqrt6 \cdot\sqrt{\left(x^3\right)^2}\cdot \sqrt x \\\\ &=3\cdot\sqrt6\cdot x^3\cdot\sqrt x \\\\ &=3x^3\sqrt{6x} \end{aligned}
54x
7
=
3
2
⋅6⋅(x
3
)
2
⋅x
=
3
2
⋅
6
⋅
(x
3
)
2
⋅
x
=3⋅
6
⋅x
3
⋅
x
=3x
3
6x
Practice
PROBLEM 2.1
Simplify.
Remove all perfect squares from inside the square root.
\sqrt{20x^8}=
20x
8
=square root of, 20, x, start superscript, 8, end superscript, end square root, equals
Explain
Want to try more problems like these? Check out this exercise.
More challenging square root expressions
PROBLEM 3.1
Simplify.
Combine like terms and remove all perfect squares from inside the square roots.
2\sqrt{7x}\cdot 3\sqrt{14x^2}=2
7x
⋅3
14x
2
=2, square root of, 7, x, end square root, dot, 3, square root of, 14, x, squared, end square root, equals
Explain
Want to try more problems like these? Check out this exercise.
What’s
1.7a + 0.3a = 0.8
Please explain step by step to get picked brainliest!
Answers
1.7a+0.3a=0.8
2a=0.8
a=0.4
What is the lengthof side d? Round tothe nearest wholenumber.
Answers
Answer:
∠E = 66
d = 47
Explanation:
The sum of angles of a triangle must be 180; thereofre.
\(\angle D+\angle E+\angle F=180\)since ∠D = 63 and ∠F = 51, we have
\(63+\angle E+51=180\)\(114+\angle E=180\)subtracting 114 from both sides gives
\(\angle E=180-114\)\(\boxed{\angle E=66}\)which is our answer!
To find the length of d we draw the traingle
Solve and graph. |3x+6/9|>=2
Answers
The solution to the inequality expression is -8/9 ≤ x ≥ 4/9
How to solve and graph the inequality expressionFrom the question, we have the following parameters that can be used in our computation:
|3x + 6/9| ≥ 2
Expand the inequality expression
So, we have
-2 ≤ 3x + 6/9 ≥ 2
Subtract 6/9 from both sides
So, we have
-24/9 ≤ 3x ≥ 12/9
Divide through the equation by 3
-8/9 ≤ x ≥ 4/9
Hence, the solution to the inequality expression is -8/9 ≤ x ≥ 4/9
The graph is attached
Read more about inequality at
https://brainly.com/question/30994664
#SPJ1

A plane is a _____ figure
Answers
Answer:
bold
Step-by-step explanation:
hshsjjsududidididiidododododokdodkdjdndndnjdudududuididjdjdjd
A plane is a two dimensional figure.
Help plz!!! Are these equations equivalent?
x = 4 - 3x
2x = 4
Answers
Answer:
no
x = 4 - 3x x = 1
2x = 4 x =2
hope this helped :D
Answer:
No. They are not equivalent. The first one would end up being x=1, while the second one would be x=2.
Step-by-step explanation:
The function h is defined by the following rule.
h(x) = 2x-3
Complete the function table.
х
4
0
- 2
2
3
5
Answers
h(4)=2(4)-3=5
h(0)=2(0)-3=-3
h(-2)=2(-2)-3=-7
h(2)=2(2)-3=1
h(3)=2(3)-3=3
h(5)=2(5)-3=7
I need help on it pls

Answers
Answer:
The answer is 15,008 you clicked the right one.
Step-by-step explanation:
Answer: your answer is right
Step-by-step explanation: i did the computation
Enter your answer in the box. Round your final answer to the nearest degree. B 6cm, A 8cm, C
Answers
The measure of Angle C is approximately 26°.
A, B, C are vertices of a triangle, where AB = 8 cm, BC = 6 cm. To determine the measure of angle C, we need to use the cosine rule.
The cosine rule states that the square of one side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the angle between them.
Mathematically, we can represent it as follows:a² = b² + c² - 2bc cos(A)where a is the side opposite to angle A, b is the side opposite to angle B, c is the side opposite to angle C.
In this case, we have AB = c = 8 cm, BC = a = 6 cm, and AC = b. We need to find the measure of angle C, which is represented as cos(C).
Using the cosine rule, we can write the equation as follows:$$\begin{aligned} b^2 &= c^2 + a^2 - 2ca\cos(C) \\ \Right arrow b^2 &= 8^2 + 6^2 - 2 \times 8 \times 6 \cos(C) \\ \Right arrow b^2 &= 64 + 36 - 96 \cos(C) \\ \Right arrow b^2 &= 100 - 96 \cos(C) \end{aligned}$$We know that b is a positive length. Hence, b² > 0 or 100 - 96 cos(C) > 0. Solving for cos(C),
we get: cos(C) < 100/96cos(C) < 1.0417Using a calculator, we can determine the inverse cosine of 1.0417 as:cos⁻¹(1.0417) = 0.4569 radians = 26.201° (rounded to the nearest degree)
Therefore, the measure of angle C is approximately 26°.
For more questions on Angle .
https://brainly.com/question/30759856
#SPJ8
Triangle ABC shown below has m B = 38°, a = 8, and c = 16. Find the area of the triangle. Round your answer to the nearest tenth and do not include units in your answer.

Answers
The area of triangle is determined as
\(A=\frac{1}{2}a\times c\times\sin B\)\(A=\frac{1}{2}\times8\times16\times\sin 38=64\sin 38^{\circ}\)\(A=39.4\text{ squnit}\)Thus the area of triangle is 39.4 sq.unit.
Find the median of the following
data set.
14,24,35,37,43,35,45,24,29,41,45,
37,19,45,44
Answers
Answer:
37,43,35 should be the answer to your game
Answer: 24
Step-by-step explanation: First of all because the number of data is 15 numbers, you know don't have to divide. Cross out the 1st and last numbers until you get to one number. I got 24
What is a solution of 3(x + 4) - x > 4?
A. -6
B. -5
C. -4
D. -3
(Please help I don’t understand)

Answers
Answer: -4 Please mark brainliest if I am right :D
Step-by-step explanation:
Let's solve your inequality step-by-step.
3(x+4)−x>4
Step 1: Simplify both sides of the inequality.
2x+12>4
Step 2: Subtract 12 from both sides.
2x+12−12>4−12
2x>−8
Step 3: Divide both sides by 2.
2x/2 > -8/2
x>−4
Answer:
x>−4
Answer:
C.-4
Step-by-step explanation:
3(x)+3(4)-x>4
3x+12-x>4
2x>-8
2x/2>-8/2
x>-4