A box contains 48 snack-sized bags of popcorn.
The weight of the box when it is empty is 5 ounces.
The weight of the box with all the bags of popcorn is 35 ounces.
What is the weight, in ounces, of each bag of popcorn? Enter your answer as a decimal.
Answers
Answer:
0.625 ounces
Step-by-step explanation:
since the box weighs 5 ounces you subtract 5 from the total and divide 48 by 30
Related Questions
PLEASE HELP ITS DUE IN 5 MIN Solve for x in the following equation and upload a picture of your work step-by-step

Answers
Answer:
1.25 = X
Step-by-step explanation:
5-2x+2=12-4x-2x
Combine all like terms here.
7-2x=12-6x
Add 2x on both sides.
7=12-4x
Subtract 12 on both sides.
-5=-4x
Divide by -4.
1.25=X
which equation models the graph?
A) y+2= -2/5(x-4)
B) y-2 = -2/5 (x-4)
C) y+2 = -3/5 (x-4)
D) y-4= -2/5 (x+2)

Answers
Suppose that the demand of a certain item is x=10+(1/p^2)
Evaluate the elasticity at 0.7
E(0.7) =
Answers
The elasticity of demand for the item at a price of 0.7 is -8.27. This means that a 1% increase in price will result in an 8.27% decrease in quantity demanded.
The elasticity of demand is a measure of how sensitive the quantity demanded of a product is to changes in its price. It is calculated by taking the percentage change in quantity demanded and dividing it by the percentage change in price. In this case, we are given the demand function x = 10 + (1/p^2), where p represents the price of the item.
To evaluate the elasticity at a specific price, we need to calculate the derivative of the demand function with respect to price and then substitute the given price into the derivative. Taking the derivative of the demand function, we get dx/dp = -2/p^3. Substituting p = 0.7 into the derivative, we find that dx/dp = -8.27.
The negative sign indicates that the item has an elastic demand, meaning that a decrease in price will result in a proportionally larger increase in quantity demanded. In this case, a 1% decrease in price would lead to an 8.27% increase in quantity demanded. Conversely, a 1% increase in price would result in an 8.27% decrease in quantity demanded.
Learn more about derivative here:
https://brainly.com/question/29144258
#SPJ11
What is the sixth term of the arithmetic sequence whose 31st and 73rd terms are 18 and 46, respectively?
Answers
The the sixth term of the arithmetic sequence whose 31st and 73rd terms are 18 and 46, respectively is 4/3.
According to the given question.
The 31st term of the arithmetic sequence is 18
And the 73rd term of the arithmetic sequence is 46
As, we know that the general term of the arithmetic sequence is given by
\(a_{n}\) = a + (n-1)
Where,
\(a_{n}\) is the nth term
a is the first term and
d is the common difference
So, the 31 term is given by
\(a_{31}\) = a + (31 - 1)d
⇒ 18 = a + 30d ...(i)
Similarly, the 73rd term is given by
46 = a + (73 - 1)d
⇒ 46 = a + 72d..(ii)
Subtract equation (i) from (ii)
46 - 18 = 72d - 30d
⇒ 28 = 42d
⇒ d = 28/42
⇒ d = 4/6
⇒ d = 2/3
Now,
18 = a + 30(2/3)
⇒ 18 = a + 20
⇒ a = -2
Therefore, the sixth term of the arithmetic sequence whose 31st and 73rd terms are 18 and 46, respectively is given by
\(a_{6}\) = -2 + (6 -1)(2/3)
⇒ \(a_{6}\) = -2 +10/3
⇒ \(a_{6}\) = 4/3
Hence, the the sixth term of the arithmetic sequence whose 31st and 73rd terms are 18 and 46, respectively is 4/3.
Find out more information about arithmetic sequence here:
https://brainly.com/question/23393976
#SPJ4
A long-distance delivery truck averages 8 miles per gallon when the truck is full. The miles per gallon improves by 20% when the truck is empty. Which expression represents the amount of gasoline used (g) in terms of the number of miles driven when full (mf) and the number of miles driven when empty (me)?
Answers
Answer:
When the truck is full: \(g_{mf} = \frac{m}{8}\)
When the truck is empty: \(g_{me} = \frac{m}{9.6}\)
Step-by-step explanation:
When the truck is full for every eight miles traveled by the vehicle, there is a cost of one gallon of fuel, therefore for every mile the cost is one eight of a gallon, with this information we can create the following expression:
\(g_{mf} = \frac{m}{8}\)
Where m is the number of miles traveled by the truck.
When the vehicle is empty, it's performance improves by 20 %, which means that for the same amount of fuel it'll travel a distance 120% of the previous one. Therefore we need to multiply 1.2 on the denominator of the last expression:
\(g_{me} = \frac{m}{8*1.2}\\\\g_{me} = \frac{m}{9.6}\)
The expression represents the amount of gasoline used (g) is,
When the truck is full (mf) is represented as \(m_f = \dfrac{m}{8}\),
And when the truck is empty (me) is represented as, \(m_e = \dfrac{m}{9.6}\)
Given that,
A long-distance delivery truck averages 8 miles per gallon when the truck is full.
The miles per gallon improve by 20% when the truck is empty.
We have to determine,
Which expression represents the amount of gasoline used (g) in terms of the number of miles driven when full (mf) and the number of miles driven when empty (me).
According to the question,
The amount of gasoline used (g) in terms of the number of miles driven when full (mf),
And The distance delivery truck averages 8 miles per gallon when the truck is full.
The amount of gasoline when the truck is full is represented as,
\(m_f = \dfrac{m}{8}\)
Then,
The miles per gallon improve by 20% when the truck is empty.
The number of miles driven when empty is represented as,
\(m_e = \dfrac{m}{8 + 8 \times 0.20}\\\\m_e = \dfrac{m}{8+ 1.6}\\\\m_e = \dfrac{m}{9.6}\)
Hence, The expression represents the amount of gasoline used (g) is,
When the truck is full (mf) is represented as \(m_f = \dfrac{m}{8}\),
And when the truck is empty (me) is represented as, \(m_e = \dfrac{m}{9.6}\).
To know more about the Linear equation click the link given below.
https://brainly.com/question/11835006?
857,963 five has a value of
Answers
Answer: 5 has a value of 50 000 2.
Hope this helps ;)
Use completing the square to solve for x in the equation (x 7) (x minus 9) = 25.
Answers
The values of \(x\) are \(1+\sqrt{89}\) and \(1-\sqrt{89}\).
To find the values of x:
Given equation: \((x+7)(x-9)=25\)
Then: \(x(x-9)+7(x-9)=25\)
Using the distributive property: \(a.(b+c)=a.b+a.c\)
\(x^{2} -9x+7x-63=25\)
Combine like terms:
\(x^{2} -2x-63=25\)
Subtract 25 from both sides and obtain:
\(x^{2} -2x-88=0\)
Using completing square form:
Add and subtract \((\frac{2}{2} )^{2} =1\) we have:
\(x^{2} -2x-88+1-1=0\\(x-1)^{2} -89=0\)
Add 89 to both sides we have:
\((x-1)^{2} =89\)
Taking square roots on both sides, obtain:
\(x-1=\) ± \(\sqrt{89}\)
Add 1 to both sides we have:
\(x=1\)±\(\sqrt{89}\)
Therefore, the values of \(x\) are \(1+\sqrt{89}\) and \(1-\sqrt{89}\).
Know more about square roots here:
https://brainly.com/question/428672
#SPJ4
The complete question is given below:
Use completing the square to solve (x + 7)(x – 9) = 25 for x.
A student prepares for an exam by studying a list of 10 problems. She can solve 7 of them. For the exam, the instructor selects 6 questions at random from the list of 10. What is the probability that the student can solve all 6 problems on the exam
Answers
This means there is approximately a 3.33% chance that the student will be able to solve all 6 problems on the exam.
We have a student who can solve 7 out of the 10 problems. The instructor will select 6 questions at random for the exam. We want to find the probability that the student can solve all 6 problems on the exam.
To determine this probability, we will use the concept of combinations. A combination is a selection of items from a larger set, where the order of the items does not matter. In this case, we will calculate the combinations of problems the student can solve and the total possible combinations of problems on the exam.
The student can solve 7 problems, so there are C(7,6) combinations of problems she can solve, where C(n,k) represents the number of combinations of n items taken k at a time. There are a total of 10 problems, so there are C(10,6) possible combinations of problems that could appear on the exam.
The probability that the student can solve all 6 problems on the exam is given by the ratio of the combinations of solvable problems to the total possible combinations of problems on the exam:
Probability = C(7,6) / C(10,6)
Using the formula for combinations, we find:
C(7,6) = 7! / (6!(7-6)!) = 7
C(10,6) = 10! / (6!(10-6)!) = 210
So, the probability that the student can solve all 6 problems on the exam is:
Probability = 7 / 210 = 1/30 ≈ 0.0333
To learn more about probability click here
brainly.com/question/30034780
#SPJ11
A field in the shape of a trapezoid has an area of 13.687.5 square yards the length of one base is 150 yards and the length of the other base is 215 yards what is the height of the trapezoid
Answers
This question is not correctly written
Complete Question
A field in the shape of a trapezoid has an area of 13,687.5 square yards the length of one base is 150 yards and the length of the other base is 215 yards what is the height of the trapezoid
Answer:
The height of the trapezoid is 75 yards
Step-by-step explanation:
Area of a Trapezoid = 1/2(b1 + b2) × h
Where b1 = Length of the first base
b2 = Length of the second base
h = height of the trapezoid
From the question
Area of the trapezoid = 13,687.5 yd²
b1 = Length of the first base = 150 yards
b2 = Length of the second base = 215 yards
h = height of the trapezoid
Hence, we have
13,687.5 = 1/2(150 + 215)h
13,687.5 = 365h/2
13,687.5 × 2 = 365h
h = 13687.5 × 2/365
h = 75 yards
Therefore, the height of the trapezoid is 75 yards.
True or false To find 7% of a number, multiply the number by 0.7
Answers
Answer:
true and it also depends on what question it is
Step-by-step explanation:
because 7% = 0.07 when doing a mathematical question it will help you a lot if you turn 7% into a decimal 0.07 and it will be more easier than doing it as a percentage.
Fiona rolls a fair dice 144 times.
How many times would Fiona expect to roll a number greater than 2?
Answers
Answer:
34
Step-by-step explanation:
the following questions about the function whose derivative id f'(x)=(x^2(x-4))/(x+6) , x does not equal -6
Answers
The given function has a derivative of f'(x) = (x^2(x-4))/(x+6), where x ≠ -6. In conclusion, the given function does not have any critical points in its domain. It is increasing on the interval (4, ∞) and decreasing on the interval (-∞, 4). There are no local maximum or minimum values for this function.
To find the critical points of the function, we set the derivative equal to zero and solve for x. However, in this case, the derivative is undefined at x = -6. Therefore, there are no critical points in the domain of the function.
To determine the increasing and decreasing intervals of the function, we analyze the sign of the derivative. The derivative is positive for x > 4 and negative for x < 4. This means the function is increasing on (4, ∞) and decreasing on (-∞, 4).
Since there are no critical points, there are no local maximum or minimum values for the function.
Learn more about critical points here:
https://brainly.com/question/31017064
#SPJ11
Finding the side length of a cube from its Volume in liters A technical machinist is asked to build a cubical steel tank that will hold 275 L of water. Calculate in meters the smallest possible inside length of the tank. Round your answer to the nearest 0.001 m. X 5 ?
Answers
The smallest possible inside length of the cubical steel tank that can hold 275 liters of water is approximately 0.640 meters.
The side length of the cube is found by converting the volume of water from liters to cubic meters, as the unit of measurement for the side length is meters.
Given that the volume of water is 275 liters, we convert it to cubic meters by dividing it by 1000 (1 cubic meter = 1000 liters):
275 liters / 1000 = 0.275 cubic meters
Since a cube has equal side lengths, we find the side length by taking the cube root of the volume. In this case, we find the cube root of 0.275 cubic meters:
∛(0.275) ≈ 0.640
Rounded to the nearest 0.001 meters, the smallest possible inside length of the tank is approximately 0.640 meters.
To know more about smallest possible inside length, refer to the link :
https://brainly.com/question/17304098#
#SPJ11
1 7/9 divided by 4/5
Answers
The answer would be 20/9
this would be because you need to convert it into an improper fraction due to it originally being 1 7/9 then you would divide 16/9 by 4/5 and simplify!
I hope this helped :)
Answer:
\(\frac{20}{9}\)
Step-by-step explanation:
hope this helps have a great rest of your day
A student has four exams grades (80,80,85, and 90) for now. If he recalculates later by including his fifth exam (95), which changed the most?
Answers
When the student recalculates their grades by including the fifth exam (95), the grade that changes the most is the lowest grade, which increases from 80 to 95.
Initially, the student had four exam grades of 80, 80, 85, and 90. These grades have a range of 10 points, from the lowest grade of 80 to the highest grade of 90. When the student includes their fifth exam grade of 95, the range increases to 15 points, as the lowest grade increases by 15 points.
The lowest grade of 80 experiences the most significant change because it increases by 15 points to become 95. In comparison, the other grades remain the same or change by smaller margins. The two initial grades of 80 remain unchanged, while the grade of 85 increases by 10 points to 95, and the grade of 90 remains the same. However, since the lowest grade undergoes the largest increase, it has the most significant impact on the overall grade calculation.
Learn more about range here:
https://brainly.com/question/15953457
#SPJ11
Which expressions are equivalent.
PLEASE HELP ME !!! (photo given)

Answers
Answer:
\(\frac{2^{5} }{6^{5} } =2^{5} 6^{-6}\)
\(=2^5\times (2^{-5} 3^{-5} )\)
\(=2^{5-5} 3^{-5}\)
\(=2^{0} 3^{-5}\)
\(=3^{-5}\)
\(OAmalOHopeO\)
Answer:
B(3^-5) and D(2^5*6^-5)
Step-by-step explanation:
I put the expression in to the calculator and put the answers into the calculator and just picked the ones that matched
Please help will mark brainliest
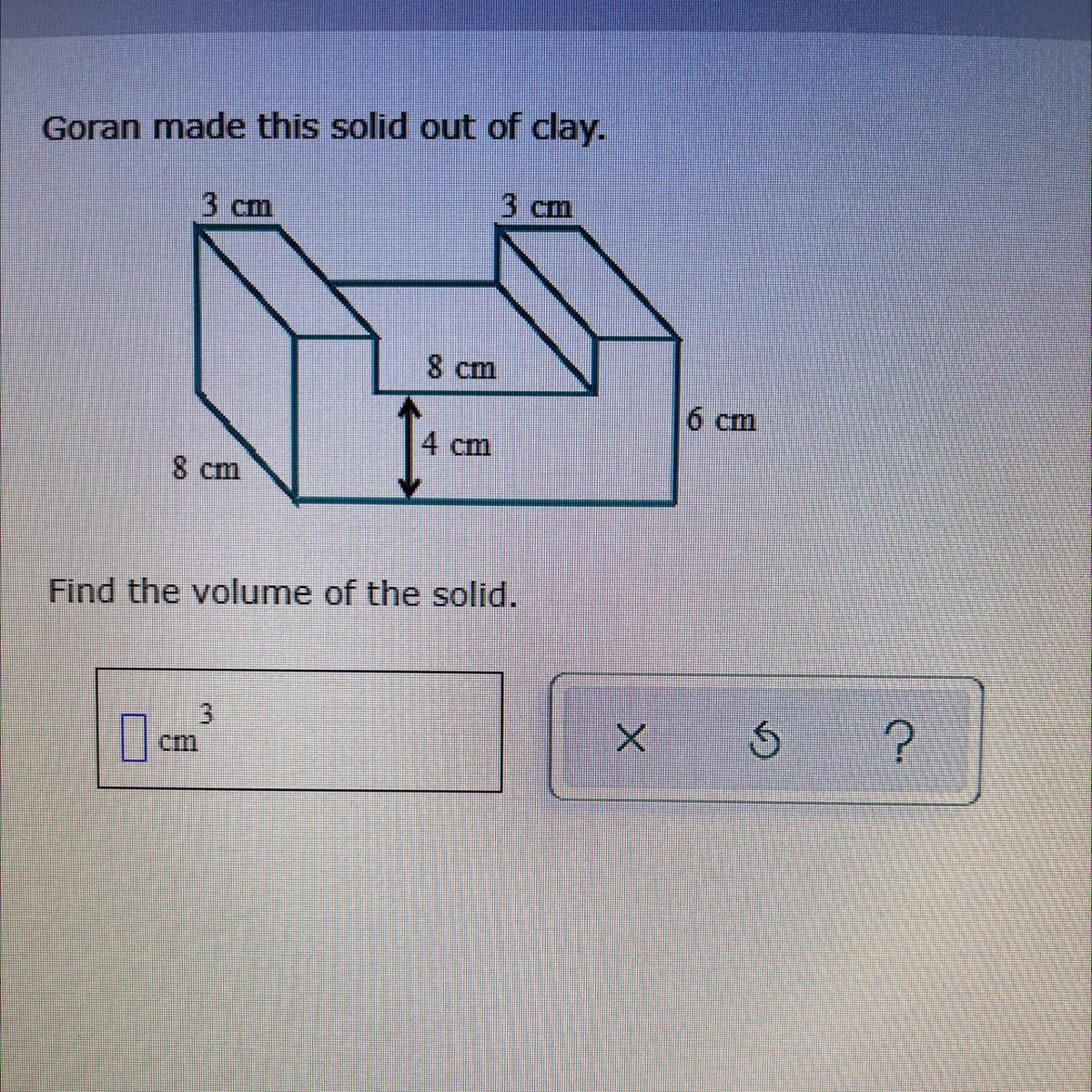
Answers
Answer:
544
Step-by-step explanation:
You can Section the figure off into 3 and find the area of each. The sum was cut off in the image, but the total is 544 :)

Step-by-step explanation:
First, solve the volume of the solid without the groove:
V1 = (14 cm)(8 cm)(6cm) = 672 cm^3
Now solve for the volume of the groove:
V2 = (8 cm)(8 cm)(2 cm) = 128 cm^3
The volume of the block that Goran made is
V = V1 - V2 = 544 cm^3
Your friend uses the percent equation to answer the question. 30 is 60% of what number? Is your friend correct? Explain your reasoning.
Answers
Yes, your friend is correct. The equation would be 30/x = 60/100. Then divide both sides by 60 to get x = 50. Therefore, 30 is 60% of 50.
Your friend is indeed using the percent equation correctly to solve the question: 30 is 60% of what number? To confirm this, let's follow the steps:
The friend's solution using the percent equation is incorrect.
To find 60% of a number, we can multiply that number by 0.6. So, if 30 is 60% of a number, we can set up the equation:
0.6x = 30
Solving for x, we get:
x = 50
Therefore, 30 is 60% of 50, not an unknown number as suggested by the friend's equation.
The friend's mistake may have been in not setting up an equation to solve for the unknown number. Instead, they may have applied the percent directly to the unknown number, which would not give the correct answer. It's important to carefully read and understand the question and set up the appropriate equation or expression to solve it.'
Learn more about Equation:
brainly.com/question/29657983
#SPJ11
Suppose x(t) = 5sinc(2007). Using properties of the Fourier transform, write down the Fourier transform and sketch the magnitude spectrum, Xo), of i) xi(t) = -4x(t-4), ii) xz(t) = e^{j400}lx(t), iii) X3(t) = 1 - 3x(t) + 1400xlx(t), iv) X(t) = cos(400ft)x(t)
Answers
i) Xi(f) = 5rect(f/2007)e^(-j2πft) | ii) Xz(f) = 5rect((f-400)/2007) | iii) X3(f) = 1 - 3*5rect(f/2007) + 1400(X(f) * X(f)) | iv) X(f) = 5rect(f/5)
Using properties of the Fourier transform, what are the expressions for the Fourier transforms of the following signals: i) xi(t) = -4x(t-4), ii) xz(t) = e^(j400)lx(t), iii) X3(t) = 1 - 3x(t) + 1400xlx(t), iv) X(t) = cos(400ft)x(t)?we'll use properties of the Fourier transform and the given function x(t) = 5sinc(2007).
i) For xi(t) = -4x(t-4):
Using the time shifting property of the Fourier transform, we have:
Xi(f) = X(f)e^(-j2πft)
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Thus, substituting the values, we have:
Xi(f) = 5rect(f/2007)e^(-j2πft)
ii) For xz(t) = e^(j400)lx(t):
Using the frequency shifting property of the Fourier transform, we have:
Xz(f) = X(f - f0)
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Substituting the value f0 = 400, we have:
Xz(f) = 5rect((f-400)/2007)
iii) For X3(t) = 1 - 3x(t) + 1400xlx(t):
Using the linearity property of the Fourier transform, we have:
X3(f) = F{1} - 3F{x(t)} + 1400F{x(t)x(t)}
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Using the Fourier transform properties, we have:
F{x(t)x(t)} = X(f) * X(f)
Substituting the values, we have:
X3(f) = 1 - 3*5rect(f/2007) + 1400(X(f) * X(f))
iv) For X(t) = cos(400ft)x(t):
Using the modulation property of the Fourier transform, we have:
X(f) = (1/2)(X(f - 400f) + X(f + 400f))
Since x(t) = 5sinc(2007), the Fourier transform X(f) of x(t) is given by:
X(f) = 5rect(f/2007)
Substituting the value f = 400f, we have:
X(f) = 5rect((400f)/2007)
Simplifying, we have:
X(f) = 5rect(f/5)
To sketch the magnitude spectrum, Xo(f), we plot the magnitude of the Fourier transform for each case using the given formulas and the properties of the Fourier transform.
Learn more about Fourier transform
brainly.com/question/1542972
#SPJ11
If you are constructing a 90% confidence interval for pd and n=30, what is the critical value? Assume od unknown.
Answers
The critical value for constructing a 90% confidence interval for a proportion with n = 30 is 1.645.
For a 90% confidence interval, the critical value is obtained from the standard normal distribution.
Since we want a two-tailed interval, we need to find the critical value for the middle 95% of the distribution.
This corresponds to an area of (1 - 0.90) / 2 = 0.05 on each tail.
To find the critical value, we can use a z-table or a calculator. For a standard normal distribution, the critical value that corresponds to an area of 0.05 in each tail is approximately 1.645.
To learn more on Statistics click:
https://brainly.com/question/30218856
#SPJ4
Solve the LP problem. If no optimal solution exists, indicate whether the feasible region is empty or the objective function is unbounded. HINT [See Example 1.) (Enter EMPTY if the region is empty. Enter UNBOUNDED if the function is unbounded.) Maximize p = x + 2y subject to x + 6y < = 15 3x + y < = 11 X > = 0, y > = 0. p = x= y=
Answers
The feasibility area is empty. The solution of the LP-problem is not possible (does not exists).
With the constraint that x and y are both non-negative, the second constraint has only one point in common with each of the first and third constraints; and those two points are different.
The feasibility region is empty; so nothing can be optimized.
Plots x + 2y = 30 (red), 2x + 2y = 30 (green) and 2x+y = 30 (blue)
The feasibility area, according to the condition, is the area of the first quadrant
- above the red line,
- below the green line,
- above the blue line.
It can be seen from the plot that this set is empty.
Therefore, the feasibility area is empty. The solution of the LP-problem is not possible (does not exists).
To learn more about linear inequations refer here
https://brainly.com/question/25799000
#SPJ4
Disclaimer
The question given by you is incomplete, so the above solution is of a similar question, and the question is
Solve the LP problem. If no optimal solution exists, indicate whether the feasible region is empty or the objective function is unbounded. HINT
Maximize p = x + y subject to
x + 2y ≥ 30
2x + 2y ≤ 30
2x + y ≥ 30
x ≥ 0, y ≥ 0.
p=
(x, y)=

3. Let f(x) = sec²x and g(x) = tan²x. Show that f'(x) = g'(x) and use the last result in Unit 7 of my notes to obtain a formula for f(x) - g(x).4. Use the Mean Value Theorem to prove that ln x≤ x - 1 for x ≥ 1.
Answers
Showed that f'(x) = g'(x), used the formula from Unit 7 to find f(x) - g(x) = 1, and proved ln x ≤ x - 1 for x ≥ 1 using the Mean Value Theorem and the function h(x) = ln x - x + 1.
To show that f'(x) = g'(x), we will differentiate both functions using the chain rule
f(x) = sec²x = (1/cosx)²
f'(x) = -2/cos³x * -sinx = 2sinx/cos³x = 2sinx/sec³x
g(x) = tan²x = (sinx/cosx)²
g'(x) = 2sinx/cos³x = 2sinx/sec³x
Therefore, f'(x) = g'(x).
Using the formula from Unit 7 of your notes, we have
f(x) - g(x) = ∫[a,b] (f'(x) - g'(x)) dx
Since f'(x) = g'(x), we can simplify this to:
f(x) - g(x) = ∫[a,b] 0 dx = 0
Therefore, f(x) - g(x) is a constant function, and we can find this constant by evaluating it at any point. Let's evaluate it at x = 0
f(0) - g(0) = sec²(0) - tan²(0) = 1 - 0 = 1
Therefore, f(x) - g(x) = 1 for all x.
To prove that ln x ≤ x - 1 for x ≥ 1 using the Mean Value Theorem, we will define a function h(x) = ln x - x + 1. We want to show that h(x) ≤ 0 for x ≥ 1.
First, note that h(1) = ln 1 - 1 + 1 = 0.
Next, we will take the derivative of h(x)
h'(x) = 1/x - 1
By the Mean Value Theorem, there exists a point c in the interval [1,x] such that
h(x) - h(1) = h'(c)(x - 1)
Substituting in the values we have
ln x - x + 1 = h(x) - h(1) = h'(c)(x - 1) = (1/c - 1)(x - 1)
Since c is between 1 and x, we know that c ≤ x, so we can rewrite this as:
ln x - x + 1 ≤ (x - 1)/c - (x - 1) = (1 - c)(x - 1)/c
Since c is greater than or equal to 1, we know that 1 - c is negative or zero, and since x is greater than or equal to 1, we know that (x - 1)/c is positive. Therefore, we have
ln x - x + 1 ≤ 0
And we have shown that h(x) ≤ 0 for x ≥ 1, which means that ln x ≤ x - 1 for x ≥ 1.
Learn more about Mean Value Theorem here
brainly.com/question/30403137
#SPJ4
write the function in terms of unit step functions. find the laplace transform of the given function. f(s)
Answers
The Laplace transformation in the given function is = 5 - 8e⁻⁷ˣ/ x
Rewrite f in terms of the unit step function:
\(f(t) \left \{ {{y=5} for 0\leq t \leq 7\atop {x=-3}} \rightfor t\leq 7\)
⇒ f(t) = 5{u(t) -u(t -7) - 3u (t -7)}
= 5u(t) - 8u (t-7)
Recall the time-shifting property of the Laplace transform:
L I u(t - c)f(t -c) I
= e⁻ᵃˣ L[f(t)]
and the Laplace transform of a constant function,
L(K) = \(\frac{k}{a}\)
So we have
L{f(t)} = 5u(t) - 8u (t-7)
= 5 L[1] - 8e⁻⁷ˣ
= 5 - 8e⁻⁷ˣ/ x
Learn more about Laplace transform:
https://brainly.com/question/14487937
#SPJ4
Please help it’s an emergency

Answers
Answer:
Down below
Step-by-step explanation:
inside of a triangle is 180 degrees. first we have to find what the inside of z and y are.
\(z=360-285\\z=75\\y=180-116\\y=64\\\)
then solve for x
\(180=75+64+x\\180=139+x\\180-139=139+x-139\\41=x\)
what is 5 1/12 + 2 5/9
Answers
Answer:
7.63888888889
Step-by-step explanation:
They probably want you to simplify too!
Determine the total number of roots f(x) = (3x^4 + 1)^2
Answers
\(f(x) = (3 {x}^{4} + 1) {}^{2} \\ f(x) = 0 \\ (3 {x}^{4} + 1) {}^{2} = 0 \\ 3x {}^{4} + 1 = 0 \\ 3x {}^{4} = -1 \\ x {}^{4} = \frac{ - 1}{3} \)
\(f(x) \: admits \: no \: real \: roots\)
How does the graph of g(x) = (x − 8)3 + 3 compare to the parent function f(x) = x3?
a. g(x) is shifted 8 units to the left and 3 units up.
b. g(x) is shifted 3 units to the right and 8 units down.
c. g(x) is shifted 8 units to the right and 3 units up.
d. g(x) is shifted 3 units to the right and 8 units up.
Answers
Answer:
The right answer is C.
Step-by-step explanation:
The parent function is:
\(f(x)=x^3\)
If something is subtracted from variable \(x\) it means the graph shifted toward right and something is added to \(y\) value then the graph is shifted up.
\(f(x)=(x-8)^3\)
graph shifted toward right by \(8\) units right
\(f(x)=(x-8)^3+3\)
graph shifted toward right by \(3\) units up
Thus the new function is:
\(g(x)=(x-8)^3+3\)
Please help 60 points for a rapid answer-In the figure below which of the following is true in circle E?


Answers
Answer:
all 3 options are true : A, B, C
Step-by-step explanation:
warning : it has come to my attention that some testing systems have an incorrect answer stored as right answer for this problem.
they say that A and C are correct.
but I am going to show you that if A and C are correct, then also B must be correct.
therefore, my given answer above is the actual correct answer (no matter what the test systems say).
originally the information about the alignment of the point F in relation to point E was missing.
therefore, I considered both options :
1. F is on the same vertical line as E.
2. F is not on the same vertical line as E.
because of optical reasons (and the - incomplete - expected correct answers of A and C confirm that) I used the 1. assumption for the provided answer :
the vertical line of EF is like a mirror between the left and the right half of the picture.
A is mirrored across the vertical line resulting in B. and vice versa.
the same for C and D.
this leads to the effect that all 3 given congruence relationships are true.
if we consider assumption 2, none of the 3 answer options could be true.
but if the assumptions are true, then all 3 options have to be true.
now, for the "why" :
remember what congruence means :
both shapes, after turning and rotating, can be laid on top of each other, and nothing "sticks out", they are covering each other perfectly.
for that to be possible, both shapes must have the same basic structure (like number of sides and vertices), both shapes must have the same side lengths and also equally sized angles.
so, when EF is a mirror, then each side is an exact copy of the other, just left/right being turned.
therefore, yes absolutely, CAD is congruent with CBD. and ACB is congruent to ADB.
but do you notice something ?
both mentioned triangles on the left side contain the side AC, and both triangles in the right side contain the side BD.
now, if the triangles are congruent, that means that each of the 3 sides must have an equally long corresponding side in the other triangle.
therefore, AC must be equal to BD.
and that means that AC is congruent to BD.
because lines have no other congruent criteria - only the lengths must be identical.
please help i need to get out of recovery mode so i can do 20 other assignments including a final exam

Answers
Answer:
3
Step-by-step explanation:
y = -3x^2 + 5x + 3
↑ this is "the number at the end/constant," and according to the question the number at the end/constant is the y-intercept
Thus, the y-intercept is 3.
What is the difference? StartFraction x + 5 Over x + 2 EndFraction minus StartFraction x + 1 Over x squared + 2 x EndFraction StartFraction x squared + 4 x minus 1 Over x (x + 2) EndFraction StartFraction x squared + 4 x + 1 Over x (x + 2) EndFraction StartFraction 4 Over negative 1 (x squared + x minus 2) EndFraction StartFraction x squared + 6 x + 1 Over x (x + 2) EndFraction
Answers
To simplify the expression, we need to find a common denominator for all the fractions.
StartFraction x + 5 Over x + 2 EndFraction minus StartFraction x + 1 Over x squared + 2 x EndFraction
= (x + 5)/(x + 2) - (x + 1)/(x(x + 2))
Next, we can combine the two fractions by finding a common denominator.
= [(x + 5)x - (x + 1)]/(x(x + 2))
= (x^2 + 4x - 1)/(x(x + 2))
StartFraction x squared + 4 x minus 1 Over x (x + 2) EndFraction StartFraction x squared + 4 x + 1 Over x (x + 2) EndFraction
We can combine these two fractions by adding the numerators and keeping the same denominator.
= (x^2 + 4x - 1)/(x(x + 2)) + (x^2 + 4x + 1)/(x(x + 2))
= (2x^2 + 8x)/(x(x + 2))
StartFraction 4 Over negative 1 (x squared + x minus 2) EndFraction
= -4/(x^2 + x - 2)
StartFraction x squared + 6 x + 1 Over x (x + 2) EndFraction
We can use partial fraction decomposition to split this fraction into simpler ones.
= (x + 3)/(x + 2) + (x + 1)/x
Now we can simplify each fraction separately.
= (x^2 + 5x + 6)/(x(x + 2)) + 1 + 1/x
= (x^2 + 5x + 6)/(x(x + 2)) + (x + 2)/(x(x + 2))
= (x^2 + 6x + 8)/(x(x + 2))
Now we can simplify the entire expression by combining all the fractions and finding a common denominator.
= (x^2 + 4x - 1)/(x(x + 2)) - 4/(x^2 + x - 2) + (x^2 + 6x + 8)/(x(x + 2))
= [((x^2 + 4x - 1) * (x^2 + x - 2)) - (4 * x(x + 2)) + ((x^2 + 6x + 8) * x)]/[x(x + 2)(x^2 + x - 2)]
= (x^4 + 6x^3 + 4x^2 - 7x - 8)/(x(x + 2)(x^2 + x - 2))
Therefore, the difference between the expressions is (x^4 + 6x^3 + 4x^2 - 7x - 8)/(x(x + 2)(x^2 + x - 2)).