A certain company reported selling 5,000 toys during the month of January and expects sales to grow at a rate of 7.5% per month until the end of that year. How many toys should the company expect to sell by the end of June of that year?
Answers
Answer:
Answer is 36,220
Step-by-step explanation:
Related Questions
Stereo Inc. sells a stereo system for $400 down and monthly payments of $90 for the next 4 years. If the interest rate is 2.75% per month, find:
a) The cost of the stereo.
Answer = $
b) The total amount of interest paid.
Answer = $
Answers
a) The cost of the stereo system is $4,760.
b) The total amount of interest paid is $1,760.
To find the cost of the stereo system, we need to calculate the sum of the down payment and the total of monthly payments over 4 years. The down payment is $400, and the monthly payment is $90 for 48 months (4 years). Thus, the total cost of the stereo system is $400 + ($90 × 48) = $4,760.
To calculate the total amount of interest paid, we need to subtract the initial principal amount (down payment) from the total cost of the stereo system. The initial principal amount is $400, and the total cost is $4,760. Therefore, the total interest paid is $4,760 - $400 = $1,760.
In summary, the cost of the stereo system is $4,760, and the total amount of interest paid is $1,760.
Learn more about initial principal here:
https://brainly.com/question/26100282
#SPJ11
solve the following system of equations using the substitution method. –6x 2y = 8 y = 3x 4 question 9 options: a) no solution b) (0, 4) c) infinitely many solutions d) (8, 8)
Answers
The correct answer is option c) infinitely many solutions..
To solve the system of equations using the substitution method, we'll substitute the value of y from the second equation into the first equation and solve for x.
Given:
-6x + 2y = 8 ---(1)
y = 3x + 4 ---(2)
Substitute equation (2) into equation (1):
-6x + 2(3x + 4) = 8
Simplify:
-6x + 6x + 8 = 8
8 = 8
We obtained a true statement (8 = 8), which means the two equations are equivalent. This solution shows that the system has infinitely many solutions.
Therefore, the correct answer is option c) infinitely many solutions..
know more about substitution method
https://brainly.com/question/22340165
#SPJ11
Jeriel gave out a survey to some students in his school about their favorite color. Students could choose between purple and blue. 484 of those surveyed said their favorite color was purple. 45% of the students surveyed said their favorite color was blue. How many students were surveyed in total?
Answers
By working with percentages, we conclude that the total number of students surveyed is 880.
How many students were surveyed in total?
First, we know that a total of N students were surveyed about what color they preferred, blue or purple.
We also know that 484 said that they preferred purple.The 45% preferred blue.Then the other 55% preferred purple, which means that the 55% of the total number of students surveyed, N, is equal to 484.
So we just need to use what we know about percentages, we will get:
484 = N*(55%/100%) = N*0.55
Now we can solve this simple linear equation to find the value of N, we will get:
484/0.55 = N = 880
In this way, we conclude that the total number of students surveyed is 880.
If you want to learn more about percentages:
https://brainly.com/question/843074
#SPJ1
help geometry ………ignore this i need 20 words
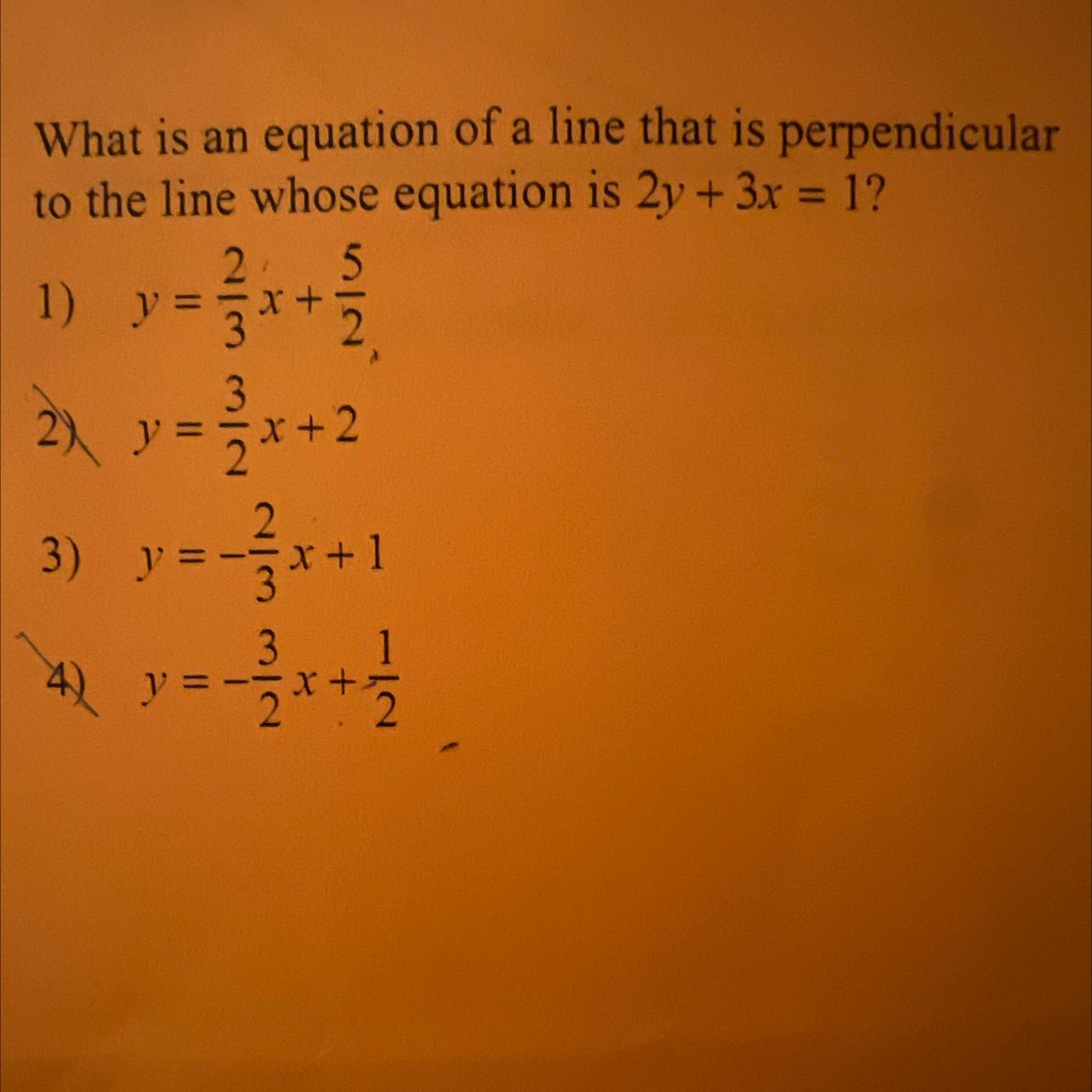
Answers
Answer:
The answer is 1
Step-by-step explanation:
1) Determine a. b if || a |= 6,|| b ||= 4 and the angle between the vectors 0 = π/3 ?
A) 24
B)-12
C) 12
D) None of the above
Answers
The dot product of vectors a and b || a |= 6,|| b ||= 4 and the angle between the vectors θ = π/3 is (c) 12.
The dot product of two vectors, we can use the formula:
a · b = ||a|| ||b|| cos(theta)
where ||a|| and ||b|| represent the magnitudes of vectors a and b, respectively, and theta is the angle between the vectors.
In this case, we are given that ||a|| = 6, ||b|| = 4, and the angle between the vectors is theta = π/3.
Substituting these values into the formula, we have:
a · b = 6 × 4 × cos(π/3)
To evaluate cos(π/3), we can use the fact that it is equal to 1/2. So we have:
a · b = 6 × 4 × 1/2
= 12
Therefore, the dot product of vectors a and b is 12.
To know more about dot product click here :
https://brainly.com/question/14455586
#SPJ4
i need help.pleaaseeeeeeeeeeIM BEGGING

Answers
Pls mark me brainliest
Please helpp
Solve this problem using order of operation
10 x( 4 + 3)
Answers
Answer:
70
Step-by-step explanation:
first step (4+3)=7
second step 10×7=70
the study would use a . the study would use simple random sampling because it would be easy to randomly select of . b. the study would use a . the study would use cluster sampling because the of fall into naturally occurring subgroups. c. the study would use a . the study would use stratified sampling because it would be important to have members from each segment of the population. d. the study is a , because the population is for it to be practical to record all of the responses.
Answers
The study would use a simple random sampling because it would be easy to randomly select. The study would use cluster sampling because the of fall into naturally occurring subgroups. The study would use stratified sampling because it would be important to have members from each segment of the population.
The study is a sample survey, because the population is for it to be practical to record all of the responses.
a. The study would use a simple random sampling because it would be easy to randomly select members of the population. Simple random sampling is a type of probability sampling that is used when the population is homogenous and every member has an equal chance of being selected for the sample.
b. The study would use cluster sampling because the members of the population fall into naturally occurring subgroups. Cluster sampling is a type of probability sampling that is used when the population is heterogeneous and can be divided into naturally occurring subgroups.
c. The study would use stratified sampling because it would be important to have members from each segment of the population. Stratified sampling is a type of probability sampling that is used when the population is heterogeneous and can be divided into segments or strata based on certain characteristics.
d. The study is a sample survey, because the population is too large for it to be practical to record all of the responses. Sample survey is a type of survey that collects data from a sample of the population, rather than the entire population. This is often done when the population is too large or when it is not practical to survey the entire population.
To know more about sampling refer here:
https://brainly.com/question/30759604
#SPJ11
Q1. (10 marks) Using only the Laplace transform table (Figure 11.5, Tables (a) and (b)) in the Glyn James textbook, obtain the Laplace transform of the following functions:
(a) cosh(2t) + cos(2t).
(b) 3e-5t + 4 – 4 sin(4t). The function "cosh" stands for hyperbolic sine and cosh
(2) emite. The results must be written in simplified form and as a single rational function. Showing result only without reasoning or argumentation will be insufficient.
Q2. (10 marks) Using only the Laplace transform table (Figure 11.5, Tables (a) and (b)) in the Glyn James textbook, obtain the Laplace transform of the following functions:
(a) + + t sin(2t) + t2 cos(3t).
(b) te2+ sin(3t), The results must be written in simplified form and as a single rational function. Showing result only without reasoning or argumentation will be insufficient.
Answers
Q1. (a) The Laplace transform of cosh(2t) + cos(2t) can be obtained as follows:
L{cosh(2t)} = 1/(s - 2) + 1/(s + 2) [Using the Laplace transform table]
L{cos(2t)} = s/(s^2 + 4) [Using the Laplace transform table]
Combining these results:
L{cosh(2t) + cos(2t)} = 1/(s - 2) + 1/(s + 2) + s/(s^2 + 4)
Simplifying further, we get:
L{cosh(2t) + cos(2t)} = (s^3 + 4s)/(s^3 + 4s^2 - 4s - 16)
(b) The Laplace transform of 3e^(-5t) + 4 - 4sin(4t) can be obtained as follows:
L{3e^(-5t)} = 3/(s + 5) [Using the Laplace transform table]
L{4} = 4/s [Using the Laplace transform table]
L{-4sin(4t)} = -16/(s^2 + 16) [Using the Laplace transform table]
Combining these results:
L{3e^(-5t) + 4 - 4sin(4t)} = 3/(s + 5) + 4/s - 16/(s^2 + 16)
Simplifying further, we get:
L{3e^(-5t) + 4 - 4sin(4t)} = (12s^2 + 152s + 106)/(s(s + 5)(s^2 + 16))
Q2. (a) The Laplace transform of t + tsin(2t) + t^2cos(3t) can be obtained as follows:
L{t} = 1/s^2 [Using the Laplace transform table]
L{tsin(2t)} = 2/(s^2 - 4) [Using the Laplace transform table]
L{t^2cos(3t)} = 2/(s^3 - 9s) [Using the Laplace transform table]
Combining these results:
L{t + tsin(2t) + t^2cos(3t)} = 1/s^2 + 2/(s^2 - 4) + 2/(s^3 - 9s)
Simplifying further, we get:
L{t + tsin(2t) + t^2cos(3t)} = (s^3 - 5s^2 + 8s + 8)/(s^3(s - 3)(s + 2))
(b) The Laplace transform of te^2 + sin(3t) can be obtained as follows:
L{te^2} = 48/(s - 2)^5 [Using the Laplace transform table]
L{sin(3t)} = 3/(s^2 + 9) [Using the Laplace transform table]
Combining these results:
L{te^2 + sin(3t)} = 48/(s - 2)^5 + 3/(s^2 + 9)
Simplifying further, we get:
L{te^2 + sin(3t)} = (s^4 - 10s^3 + 40s^2 -
To learn more about Laplace : brainly.com/question/30759963
#SPJ11
Part B
Ariel states that a mockingbird beats
its wings approximately 0.07 times
per second. Is Ariel correct?
Explain.
Answers
Ariel is not correct because mockingbird beats its wings 14 times per second.
What is Slope?A line's slope is determined by how its y coordinate changes in relation to how its x coordinate changes. y and x are the net changes in the y and x coordinates, respectively. Therefore, it is possible to write the change in y coordinate with respect to the change in x coordinate as,
m = Δy/Δx where, m is the slope
From the table the slope of the data is
= (1260 - 420)/ (90-30)
= 840 - 60
= 14
So, the mockingbird beats its wings approximately 14 times per second.
Thus, ariel is not correct.
Learn more about Slope here:
https://brainly.com/question/3605446
#SPJ1
Find the length of UC
A. 54
B. 4
C. 39
Answers
Either take the photo of that question or take screenshot and attach it. The question is not complete.
solving by elimination
7x-y=19
2x-3y=19
Answers
Answer:
2x + y = -2, x + 2y = 2
4x + y - 2z = 0, 2x+ 3z = 9 , -6x - 2y + z = 0
x + y = 4 , x - y = 2
Step-by-step explanation:
Answer:
x=2 and y=−5
Step-by-step explanation:
Let's solve your system by elimination.
7x−y=19;2x−3y=19
Multiply the first equation by -3,and multiply the second equation by 1.
−3(7x−y=19)
1(2x−3y=19)
Becomes:
−21x+3y=−57
2x−3y=19
Add these equations to eliminate y:
−19x=−38
Then solve−19x=−38for x:
−19x=−38
(Divide both sides by -19)
x=2
Now that we've found x let's plug it back in to solve for y.
Write down an original equation:
7x−y=19
Substitute2forxin7x−y=19:
(7)(2)−y=19
−y+14=19(Simplify both sides of the equation)
−y+14+−14=19+−14(Add -14 to both sides)
−y=5
y=-5
7x2+6=23x
a. What is the first step when solving this quadratic equation?
b. What are the solutions to the equation?
Answers
Answer:
x = 3, x = \(\frac{2}{7}\)
Step-by-step explanation:
(a)
The first step is to subtract 23x from both sides, that is
7x² - 23x + 6 = 0 ← in standard form
(b)
Consider the factors of the product of the coefficient of the x² term and the constant term which sum to give the coefficient of the x- term.
product = 7 × 6 = 42 and sum = - 23
The factors are - 21 and - 2
Use these factors to split the x- term
7x² - 21x - 2x + 6 = 0 ( factor the first/second and third/fourth terms )
7x(x - 3) - 2(x - 3) = 0 ← factor out (x - 3) from each term
(x - 3)(7x - 2) = 0
Equate each factor to zero and solve for x
x - 3 = 0 ⇒ x = 3
7x - 2 = 0 ⇒ 7x = 2 ⇒ x = \(\frac{2}{7}\)
Determine the most appropriate model for the data in the table. x y 0 4 1 8 2 15.9 3 32 4 65.2 5 128 Select from the drop-down menu to correctly complete the statement. A(n) Choose... model is the most appropriate model for the given data.
Answers
The exponential model is the most appropriate model for the given data.
How to determine the appropriate model?The table of values is given as:
x 0 1 2 3 4 5
y 4 8 15.9 32 65.2 128
From the above table, we have the following highlights:
The value of x increases by 1The value of y doubles by (approximately) 2The above highlights is similar to an exponential model, because an exponential model has a constant multiplicative rate
Hence, the appropriate model is the exponential model
Read more about exponential models at:
https://brainly.com/question/11464095
#SPJ1
HELP ASAP! Pls and thx! Need help.

Answers
Answer:
y = -3x + 22
Step-by-step explanation:
To find m, find the change in y and divide it by the change in x.
For example, the change in y between 19 and 13 is -6. Then determine the change in x. For example, since we determined the change in 19 and 13, let's look at the change in the x coordinates that pair with 19 and 13: 1 and 3. The change in x between 1 and 3 is 2. Now divide the change in y by the change in x: -6/2 = -3. So now we have the equation y = -3x + b, but we still need to figure out b, or the y-intercept. To do this, we need to figure out a pattern in the table to find out what y is equal to when x = 0, the definition of a y-intercept. From just the table alone, it looks like for every 2 units the x-coordinate decreases, the y-coordinates increases by 6. We could also just as easily say that for every 1 unit the x-coordinate decreases, the y-coordinate increases by 3. From this definition, if we look at the coordinate (1, 19), if we were to decrease 1 from the x-coordinate, we would have to increase the y-coordinate by 3 which we can write as (x - 1, y + 3). So, we would get (0, 22). So, when x = 0, y = 22.
what is the surface area of the image below?

Answers
Answer:
Total Surface Area = 24.887864491364 inches^2
itz pretty ez unless ur lazy tho
if you are dividing 1.7 by 8.5 how many places to the right will you need to move the decimal point in the divisor and dividend
Answers
Answer:
To divide 1.7 by 8.5, you will need to move the decimal point one place to the right in the divisor and the dividend. This would result in 17 and 85 as the new divisor and dividend respectively, and the division would be performed as 17/85.
What’s the slope of line 1

Answers
Answer:
the slope in line 1 is a
Step-by-step explanation:
Answer:
4
Step-by-step explanation:
→ Utilise the gradient formula
(y₂ - y₁) ÷ (x₂ - x₁)
→ Substitute in the numbers
(2 - -6) ÷ (1--1)
→ Simplify
4
Find the sum of the first 7 terms of the following series. Round to the nearest whole
number.
8, 6, 9/2, …
Answers
The sum of the first 7 terms of the following series round to the nearest whole number is 26.
What is the sum of terms of a geometric series?
When all the terms of a geometric sequence are added, then that expression is called geometric series.
Lets suppose its initial term is , multiplication factor is r
and let it has total n terms, then, its sum is given as:
\(S_n = \dfrac{a(r^n-1)}{r-1}\)
(sum till nth term)
We are given that;
The series= 8, 6, 9/2, …
n=7
Now To find the sum of the first 7 terms of the series, we need to add up the first 7 terms. The first term is 8, the second term is 6, and the third term is 9/2. We can see that each term is obtained by subtracting 2 from the previous term and then dividing by 2. So we can write out the first few terms:
8, 6, 9/2, 7/4, 5/8, 9/16, 7/32, ...
To find the sum of the first 7 terms, we can add them up:
8 + 6 + 9/2 + 7/4 + 5/8 + 9/16 + 7/32 = 25.625
Rounding to the nearest whole number, we get a sum of 26.
Therefore, answer of the given series will be 26.
Learn more about sum of terms of geometric series here:
brainly.com/question/1607203
#SPJ1
evaluate the iterated integral. 8 6 2z 0 ln(x) 0 xe−y dy dx dz
Answers
To evaluate the iterated integral ∫∫∫ 2z ln(x) xe^(-y) dy dx dz over the limits 0 ≤ y ≤ 6, 0 ≤ x ≤ 8, and 0 ≤ z ≤ 1, we begin by integrating the innermost integral with respect to y first, then the middle integral with respect to x, and finally the outermost integral with respect to z.
So, integrating with respect to y first, we get:
∫∫∫ 2z ln(x) xe^(-y) dy dx dz = ∫∫∫ 2z ln(x) (-e^(-y) + C) dx dz
where C is the constant of integration.
Next, integrating with respect to x, we get:
∫∫∫ 2z ln(x) (-e^(-y) + C) dx dz = ∫∫ 2z (-ln(x)e^(-y) + Cx) |_0^8 dz
= ∫∫ 16z(ln(8)e^(-y) - C) dz
= 16(ln(8)e^(-y) - C)z^2/2 |_0^1
= 8(ln(8)e^(-y) - C)
Finally, integrating with respect to z, we get:
∫∫ 8(ln(8)e^(-y) - C) dz = (8/2)(ln(8)e^(-y) - C)(1^2 - 0^2)
= 4(ln(8)e^(-y) - C)
Therefore, the value of the iterated integral over the given limits is 4(ln(8)e^(-6) - C), where C is a constant of integration.
FOR MORE INFORMATION ON integral SEE;
https://brainly.in/question/4615818
#SPJ11
Using the notation of the previous problem, prove that for sets A, B, C, D ∈ P(X). AΔB = CΔD <---> AΔC = BΔD.
Answers
To prove that AΔB = CΔD if and only if AΔC = BΔD, we need to show two implications:
If AΔB = CΔD, then AΔC = BΔD
If AΔC = BΔD, then AΔB = CΔD
Let's start with implication 1:
Suppose AΔB = CΔD. This means that every element that is in A or B, but not both, is also in C or D, but not both. Similarly, every element that is in C or D, but not both, is also in A or B, but not both.
Now consider AΔC. This is the set of elements that are in A or C, but not both. We can split this set into two parts: (i) the elements that are in A but not in C, and (ii) the elements that are in C but not in A.
For part (i), we know that these elements are either in B or not in B, because if an element is in A but not in C, it must be in B (since B is the set of elements that are in A but not in AΔB). Similarly, for part (ii), we know that these elements are either in D or not in D.
Therefore, we can write AΔC = (A∩B')∪(C∩D').
Similarly, we can write BΔD = (B∩A')∪(D∩C').
Now, since AΔB = CΔD, we have that (A∩B')∪(C∩D') = (B∩A')∪(D∩C'). Rearranging this equation, we get (A∩C')∪(C∩A') = (B∩D')∪(D∩B'). This means that AΔC = BΔD, which proves implication 1.
Now let's move on to implication 2:
Suppose AΔC = BΔD. This means that every element that is in A or C, but not both, is also in B or D, but not both. Similarly, every element that is in B or D, but not both, is also in A or C, but not both.
Now consider AΔB. This is the set of elements that are in A or B, but not both. We can split this set into two parts: (i) the elements that are in A but not in B, and (ii) the elements that are in B but not in A.
For part (i), we know that these elements are either in C or not in C, because if an element is in A but not in B, it must be in C (since C is the set of elements that are in A but not in AΔC). Similarly, for part (ii), we know that these elements are either in D or not in D.
Therefore, we can write AΔB = (A∩C')∪(B∩D').
Similarly, we can write CΔD = (C∩A')∪(D∩B').
Now, since AΔC = BΔD, we have that (A∩C')∪(B∩D') = (C∩A')∪(D∩B'). Rearranging this equation, we get (A∩D')
More related to implications: https://brainly.com/question/29506010
#SPJ11
Find the number that makes the ratio equivalent to 2:4
16:
Answers
Step by step:no
please help QUICK i will make u brainliest

Answers
Answer:
1. 1.25 \(g/cm^{3}\)
2. 1.36 \(g/cm^{3}\)
3. 1.04 \(g/cm^{3}\)
4. 0.79 \(g/cm^{3}\)
Step-by-step explanation:
Density = Mass/Volume
1. 15g/\(12cm^{3}\) = 1.25 \(g/cm^{3}\)
2. 7.5g/\(5.5cm^{3}\) = 1.36 \(g/cm^{3}\)
3. 26g/\(25cm^{3}\) = 1.04 \(g/cm^{3}\)
4. 1350g/\(1700cm^{3}\) = 0.79 \(g/cm^{3}\)
Answer:
1. 1.25
2. 1.36
3. 1.04
4. 0.79
Is the triangle isosceles, equilateral, or
neither?
8
8.
A
8.
A. isosceles
B. equilateral
C. neither

Answers
Answer:
Equilateral
Step-by-step explanation:
Cause all the sides are equal which implies all the angles are equal...
Answer:
B
Step-by-step explanation:
Equilateral because all the three sides are equal
3/m = 45/50 HELP THIS IS HARD, WILL GIVE BRAINLIST IF CORRECT ANSWER AND ANSWERED RIGHT
Answers
Step-by-step explanation:
Simplify for m by using algebra.
Divide each side by 3:
\( \frac{3m}{3} = \frac{0.95}{3} \)
\( m = \frac{19}{60} \)
2 quarter’s=. Pints
Help
Answers
Answer:
2 quarts= 4 pints
Step-by-step explanation:
multiply the volume value by 2
< > Question 5 Find dy for y = dx cos(4x) 10e23 dy = 11 dx Question Help: Video Written Exan Submit Question
Answers
We have found that dy/dx = -4xsin(4x) + cos(4x) + 10e23 for y = x cos(4x) + 10e23.
We can use the product rule of differentiation to find dy/dx for y = x cos(4x) + 10e23.
The product rule states that if y = u(x)v(x), then
dy/dx = u(x)dv/dx + v(x)du/dx.
In this case, we have u(x) = x and v(x) = cos(4x) + 10e23. We can differentiate each factor separately to get:
du/dx = 1
dv/dx = -4sin(4x)
Substituting these values into the product rule formula, we get:
dy/dx = x(-4sin(4x)) + (cos(4x) + 10e23)(1)
Simplifying, we have:
dy/dx = -4xsin(4x) + cos(4x) + 10e23
Therefore, we have found that dy/dx = -4xsin(4x) + cos(4x) + 10e23 for y = x cos(4x) + 10e23.
Learn more about differentiation here:
https://brainly.com/question/31383100
#SPJ11
can someone please help

Answers
Answer:
x = 13
Step-by-step explanation:
→ Remember the amount of degrees a triangle sums to
180°
→ Make an equation
8x - 44 + 8x - 44 + 8x - 44 = 180
→ Simplify
24x - 132 = 180
→ Add 132 to both sides
24x = 312
→ Divide both sides by 24
x = 13
If x = 1 2 , then x − 1 2 = 0. this is the same as = 0. in completely factored form, f(x) = .
Answers
If x = 1 2 , then f( 1 2) = 0. this is the same as = 0. in completely factored form, f(x) = x-12.
What is a function?
A function from A to B is a rule that assigns to each element of A a unique element of B. A is called the domain of the function and B is called the codomain of the function.
There are different operations on functions like addition, subtraction, multiplication, division and composition of functions.
then f(x) = x-12
because if we put x= 12
then we get f(x) = 0
learn more about of function here
https://brainly.com/question/29306423
#SPJ4
Optimization A cone is made from a circular sheet of radium R by cutting out a sector and gluing the cut edges. What is the maximum volume of the cone
Answers
The cone should have its maximum volume. V=1/*3r2h is the formula for calculating the volume V of a cone with height h and radius r.
How do you find the maximum volume of a cone?The cone has a volume of
V=πr2h/3
Therefore, we must calculate the values of r and h in terms of R. R is the diameter of the cone's top-circular circle, and h is the cone's height.
R is the cone's slant height, and it serves as the hypotenuse of a right triangle.
R2 = h2 + r2, or r2 = R2-h2.
So V = (1/3)π
[R2-h2]
h = (π/3)[R2h-h3]
You must take the derivative of the cone's volume, set it to zero, then solve for h to determine the cone's maximum volume.
dV/dh=(π/3)[R2-3h2]
R2-3h2=0 --> h2=R2/3 -> h = R/√3
Now we can determine r:
r2=R2-R2/3 = (2/3)R2
The volume formula with r and h substituted:
V = (π/3)
r2h = (π/3)(2R2/3)
(R/√3)
V(R)=2πR3/(9√3)
The complete question is:
A cone-shaped drinking cup is made from a circular piece of paper of radius R by cutting out a sector and joining the edges CA and CB. Find the maximum capacity of such a cup (Your answer may depend on R).
To learn more about volume of the cone refer to:
https://brainly.com/question/1082469
#SPJ4