A consumer charges a $2,530. 16 purchase on a credit card. The card has a daily interest rate of 0. 42%. If the balance is paid off at the end of 30 days, how much interest will the consumer pay? a. $0. 32 b. $3. 19 c. $31. 88 d. $318. 78.
Answers
The interest the customer would pay is $318.78.
Interest can be described as the cost of borrowing. It is the amount of money a borrower has to pay to the lender.
Interest = amount borrowed x interest rate
Daily interest = $2,530.16 x 0.42%
$2,530.16 x 0.0042 = 10.63
Monthly interest = 10.63 x 30 = $318.80
To learn more about interest, please check: https://brainly.com/question/25811386
Related Questions
The Lopez Family meets with a financial planner who advises them to save 15% of their income per month for college savings for their children. They earn $8,540 per month. How much will the Lopez family save each month for future college expenses?
Record your answer and fill in the bubbles on your answer document. Be sure to use the correct place value.
Answers
Answer:
$1281.00
Step-by-step explanation:
8540*15%=1281
3. The area of a square is 169 cmWhat is the length of the diagonal of
the square?
Answers
Answer:
18.4 cm
Step-by-step explanation:
A square has equal sides. Let's say one side is x. The area would be x^2. We know the area to be 169 cm^2, so:
x^2 = 169 cm^2
x = 13 cm
The diagonal, z, would form a right triangle with two sides of length 13 cm. The Pythagorean theorem can be used:
13^2 + 13^2 = z^2
z^2 = 338
z = 18.38 cm, or 18.4 cm
Look at this square. Find the value of
S.
S
Perimeter = 16 miles
S =
miles
Answers
The value of S, which represents the length of each side of the square, is 4 miles.
To find the value of S, we need to determine the length of each side of the square. Given that the perimeter of the square is 16 miles, we can use the formula for the perimeter of a square, which is 4 times the length of a side.
Perimeter = 4 × S
Given that the perimeter is 16 miles, we can substitute this value into the equation:
16 = 4 × S
To solve for S, we divide both sides of the equation by 4:
16 ÷ 4 = S
4 = S
Therefore, S, which stands for the square's side lengths, has a value of 4 miles.
So, S = 4 miles.
This means that each side of the square measures 4 miles, and the square has equal sides and right angles at each corner.
for such more question on value
https://brainly.com/question/4344214
#SPJ8
Andrew Needs 995 tickets to get the prize he wants At the arcade. He Already has 319 tickets and can earn 4w tickets each time he plays an game. How many games will he have to play in order to have enough tickets to win the prize he wants.
Answers
To win the e prize
What is the formula to find P(A) for a series of simple events (ex: tossing a coin and selecting a number at the same time)
Answers
The probability of event A is P(A) = 1/4 or 0.25.
The formula to find P(A) for a series of simple events is:
P(A) = (number of outcomes that satisfy the event A) / (total number of possible outcomes)
For example, if you are tossing a coin and selecting a number at the same time, and event A is defined as getting a head and an even number, then:
- The number of outcomes that satisfy event A is 1 (getting a head and an even number, i.e., H2)
- The total number of possible outcomes is 4 (H1, H2, T1, T2)
- Therefore, the probability of event A is P(A) = 1/4 or 0.25.
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
Find the exact value of cos J in simplest form.
√29
14
15
H
Answers
The cosine of angle J is given as follows:
\(\cos{J} = \frac{14\sqrt{2}}{49}\)
What are the trigonometric ratios?The three trigonometric ratios are the sine, the cosine and the tangent of an angle, and they are obtained according to the rules presented as follows:
Sine = length of opposite side/length of hypotenuse.Cosine = length of adjacent side/length of hypotenuse.Tangent = length of opposite side/length of adjacent side = sine/cosine.For the angle J in this problem, we have that:
4 is the adjacent side.\(\sqrt{98}\) is the hypotenuse.Hence the cosine of angle J is given as follows:
\(\cos{J} = \frac{4}{\sqrt{98}} \times \frac{\sqrt{98}}{\sqrt{98}}\)
\(\cos{J} = \frac{4\sqrt{98}}{98}\)
\(\cos{J} = \frac{2\sqrt{98}}{49}\)
As 98 = 2 x 49, we have that \(\sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2}\), hence:
\(\cos{J} = \frac{14\sqrt{2}}{49}\)
A similar problem, also about trigonometric ratios, is given at brainly.com/question/24349828
#SPJ1

3x + 2 for x = 5 plz
Answers
3x + 2
3 (5) +2
15 + 2
17what is the mean of 40 100 25 90 85 95
Answers
Mean is also known as an average value amoung a set of data points, results, and tests.
Mathematically, mean ( average ) is defined as a weighted sum of data points. This can be expressed in a symbolic form as follows:
\(\text{Mean = }\sum ^N_{n\mathop=1}(\frac{x_n}{N})\)Where,
\(\begin{gathered} x_n\colon\text{ The set of data points and type of data} \\ N\colon\text{ The total number of data-points} \end{gathered}\)We are given with the following set of data points:
\(x_1=40,x_2=100,x_3=25,x_4=90,x_5=85,x_6\text{ = 95}\)And we have a total of:
\(N\text{ = 6 data points }\)We will go ahead and plug in the respective values given into the formula for determining the mean value as follows:
\(\text{Mean = }\frac{x_{1\text{ }}+x_2+x_3+x_4+x_5+x_6}{N}\)Plug in the respective data points as follows:
\(\text{Mean = }\frac{40\text{ + 100 + 25 + 90 + 85 + 95}}{6}\)Evaluate as follows:
\(\begin{gathered} \text{Mean = }\frac{435}{6} \\ \text{\textcolor{#FF7968}{Mean = }}\textcolor{#FF7968}{72.5} \end{gathered}\)The mean ( average ) value for the given set of data points is:
\(\textcolor{#FF7968}{72.5}\)Use the graph below to answer the question.

Answers
The statements that are true are:
a. The rate of change of segment T is decreasing
b. Difference between the rate of change of segments S and R is 3½
How to Find Rate of ChangeRate of change (slope) = change in y / change in x = rise/runRate of change for horizontal line/graph are always zero.To determine which statements are true, find the rate of change of each segment in the graph.
Rate of change for Segment R:
Segment R is horizontal, therefore the rate of change = 0.
Rate of change for Segment S:
Rate of change = rise/run = 7/2 = 3½.
Rate of change for Segment T:
Rate of change = rise/run = 8/-8 = -1.
Rate of change for Segment U:
Rate of change = rise/run = 5/3 = 2⅔.
The rate of change of segment T is negative, therefore, it is decreasing. (Option 1 is true).
Difference between Rate of change of segment S and R = 3½ - 0 = 3½. (Option 2 is also true).
Rate of change for segment T, -1, is less than rate of change for segment S, 3½. (Option 3 is not true).
Option 4 is false. Rate of change for segment U is rather 2⅔.
Option 5 is also not true. Segment R has a rate of change of 0.
Therefore, the statements that are true are:
a. The rate of change of segment T is decreasing
b. Difference between the rate of change of segments S and R is 3½
Learn more about rate of change on:
https://brainly.com/question/8728504
given triangle abc, how many possible triangles can be formed for the following conditions: ab = 37cm, ac = 26cm, angle b = 32.5°
Answers
Given the lengths of the two sides and the angle between them, only one triangle can be created under the given circumstances.
1. Given that angle B is 32.5°, side AB is 37 cm, side AC is 26 cm, etc.
2. Calculate side BC using the Law of Cosines:
BC = (2(AB)(AC)cosB) + (AB)(AC)2
3. Input the values that are known: BC = (37 2 + 26 2 - 2(37)(26)cos32.5°)
4. Condense: BC = (1369 plus 676 minus 1848 cos 32.5 °)
5. Determine BC =. (2095 - 1539.07)
6. Condense: BC = 556.93
7. Determine BC as 23.701 cm.
8. Since the lengths of the two sides and the angle between them are specified, only one triangle can be formed under the current circumstances.
By applying the Law of Cosines, we can determine the length of the third side, BC, given that side AB is 37 cm, side AC is 26 cm, and angle B is 32.5°. In order to perform this, we must first determine the cosine of angle B, which comes out to be 32.5°. Then, we enter this value, together with the lengths of AB and AC, into the Law of Cosines equation to obtain BC.BC = (AB2 + AC2 - 2(AB)(AC)cosB) is the equation. BC is then calculated by plugging in the known variables to obtain (37 + 26 - 2(37)(26)cos32.5°). By condensing this formula, we arrive at BC = (1369 + 676 - 1848cos32.5°). Then, we calculate BC as BC = (2095 - 1539.07), and finally, we simplify to obtain BC = 556.93. Finally, we determine that BC is 23.701 cm. Given the lengths of the two sides and the angle between them.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
Select the correct answer.
What are the x-intercept and the y-intercept of this function?
fx) = 4x + 12
O A.
The x-intercept is (3,0), and the y-intercept is (0,-12).
OB.
The x-intercept is (-3,0), and the y-intercept is (0,-12).
O C.
The x-intercept is (3,0), and the y-intercept is (0,12).
OD.
The x-intercept is (-3,0), and the y-intercept is (0,12).
Answers
Answer:
D- The x-intercept is (-3,0), and the y-intercept is (0,12).
Step-by-step explanation:
right on plato/edmentum
The solution is Option D.
The x-intercept is ( -3 , 0 ), and the y-intercept is ( 0 , 12 )
What is an Equation of a line?
The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation of the line be f ( x ) = y
And , the equation is
f ( x ) = 4x + 12
So , y = 4x + 12
To find the x intercept of the line ,
Substitute the value of y = 0
So , 0 = 4x + 12
Subtracting 12 on both sides , we get
4x = -12
Divide by 4 on both sides , we get
x = -3
Therefore , the x-intercept is ( -3 , 0 )
Now , To find the y intercept of the line ,
Substitute the value of x = 0
So , y = 12
Therefore , the y-intercept is ( 0 , 12 )
Hence , The x-intercept is ( -3 , 0 ), and the y-intercept is ( 0 , 12 )
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ2
In 2009,the population of brazil was 191.5 million. this represented a decrease in population of $3.7%from 2000 .what was the population of brazil in 2000 round to the nearest tenth of a million
Answers
Population in the year 2000= 198.85million
From the question, we get to know that the population in 2009 was 191.5 million.
And we have to find the population of the year 2000 which is 3.7%more than the 2009 population.
So let us take the population of the year 2000 to be x.
From the above, we can form an equation:
(population of year 2000 * ( 100-3.7 /100) = (population of year 2009)
i.e., x * 100-3.7/ 100 = 191.5
x * 96.3 = 191.5
x = 198.85
So 198.85 is the population of 2000.
To know more about the Percentage Problem refer to the link given below:
https://brainly.com/question/16193777
#SPJ4
mary is walking on the plane starting from the point (-1,5); she reaches the point (2,3) after 4 seconds and continues on. at the exact time mary crosses the y axis, bob is standing at the origin and starts running from the origin towards the point (6,6) at a speed of 3√2 units/sec. write a formula for the distance between mary and bob t seconds after mary starts moving (hint, use a multipart function).
Answers
the formula for the distance between Mary and Bob at time t seconds after Mary starts moving is:
D(t) = √[( (-1 - (9/4)√2)t )² + ( (5 - (5/2)√2)t )²]
To find the distance between Mary and Bob at time t seconds after Mary starts moving, we can break down the problem into two parts: the distance covered by Mary and the distance covered by Bob.
Let's consider the distance covered by Mary first. We are given that Mary reaches the point (2,3) after 4 seconds and continues moving. We can represent Mary's position at time t seconds after she starts moving with the equation:
Mary's position: (x_m(t), y_m(t))
To find the equation for Mary's position, we need to determine the velocity components for Mary. We know that Mary travels from (-1,5) to (2,3) in 4 seconds, so the velocity components are:
Velocity in the x-direction: (2 - (-1)) / 4 = 3/4
Velocity in the y-direction: (3 - 5) / 4 = -1/2
Now, we can write the equations for Mary's position as functions of time:
x_m(t) = (-1) + (3/4)t
y_m(t) = 5 + (-1/2)t
Next, let's consider the distance covered by Bob. Bob starts at the origin (0,0) and moves towards the point (6,6) at a speed of 3√2 units/sec. We can represent Bob's position at time t seconds after Mary starts moving with the equation:
Bob's position: (x_b(t), y_b(t))
Since Bob moves at a constant speed towards (6,6), his position can be expressed using a linear equation:
x_b(t) = (3√2)t
y_b(t) = (3√2)t
Now, to find the distance between Mary and Bob at time t seconds, we can use the distance formula:
Distance between Mary and Bob: D(t) = √[(x_m(t) - x_b(t))² + (y_m(t) - y_b(t))²]
Plugging in the equations for Mary's and Bob's positions:
D(t) = √[(x_m(t) - (3√2)t)² + (y_m(t) - (3√2)t)²]
Simplifying and combining like terms:
D(t) = √[( (-1) + (3/4)t - (3√2)t )² + ( 5 + (-1/2)t - (3√2)t )²]
D(t) = √[( (-1 - (9/4)√2)t )² + ( (5 - (5/2)√2)t )²]
Therefore, the formula for the distance between Mary and Bob at time t seconds after Mary starts moving is:
D(t) = √[( (-1 - (9/4)√2)t )² + ( (5 - (5/2)√2)t )²]
Learn more about distance here
https://brainly.com/question/23366355
#SPJ4
Eight years ago you mvested \( \$ 1.000 \) in stocks. Today your account is worth \( \$ 2.839 .42 \). What rate of refum dist your stocks earn frounded to the nearest whole percent)? Select one A. 156
Answers
The rate of return on the stocks over the eight-year period, rounded to the nearest whole percent, is approximately 184%.
To calculate the rate of return, we can use the formula:
Rate of Return = (Final Value - Initial Value) / Initial Value
In this case, the initial value of the investment was $1,000, and the final value is $2,839.42. Plugging these values into the formula, we get:
Rate of Return = ($2,839.42 - $1,000) / $1,000 = $1,839.42 / $1,000 ≈ 1.83942
To convert this decimal to a percentage, we multiply it by 100:
Rate of Return ≈ 1.83942 * 100 ≈ 183.942
Rounding this to the nearest whole percent, we get 184%. Therefore, the rate of return on the stocks is approximately 184%.
It's important to note that there seems to be a discrepancy between the given final value of $2,839.42 and the expected result of 184%. The correct calculation of the rate of return should yield a result closer to 184% rather than 156%.
learn more about rate of return here:
https://brainly.com/question/17164328?
#SPJ11
at the forrester manufacturing company, one repair technician has been assigned the responsibility of maintaining four machines. for each machine, the probability distribution of the running time before a breakdown is exponential, with a mean of 8 hours. the repair time also has an exponential distribution, with a mean of 4 hours. (a) find the probability distribution of the number of machines not running, and the mean of this distribution. (b) what is the expected fraction of time that the repair technician will be busy?
Answers
(a) The probability distribution of the number of machines not running, and the mean of this distribution is 0.899.
(b)The expected fraction of time that the repair technician will be busy is 88.9% of the time.
(a) Let X be the number of machines not running. At that point, X can take on values 0, 1, 2, 3, or 4. We will discover the likelihood conveyance of X as takes after:
P(X = 0) = P(all machines are running) = \(e^(-84)^4\)/4! = 0.302
P(X = 1) = P(one machine isn't running) = (4)(\(e^(-84)^3\)/3!) = 0.393
P(X = 2) = P(two machines are not running) = (6)(\(e^(-84)^2\)/2!) = 0.236
P(X = 3) = P(three machines are not running) = (4)(\(e^(-84)^1\)/1!) = 0.067
P(X = 4) = P(all machines are not running) = \(e^(-8*4)^0\)/0! = 0.002
The cruel(mean) of this dispersion is E(X) = (0)(0.302) + (1)(0.393) + (2)(0.236) + (3)(0.067) + (4)(0.002) = 0.899.
(b) Let Y be the division of time that the repair specialist is active. At that point, Y can be communicated as
Y = T/(T + R),
where T is the full time that machines are not running
and R is the entire time that went through on repairs.
We know that
T has an Erlang dispersion with parameters
n = 4 and λ = 1/8 (since the running time of each machine has exponential dissemination with cruel 8 hours).
Subsequently, the anticipated esteem of T is E(T) = n/λ = 32 hours.
Additionally, R has an exponential dispersion with cruel 4 hours,
so E(R) = 4 hours. In this way, we have:
E(Y) = E(T/(T + R))
= E(T)/E(T + R)
= 32/(32 + 4)
= 0.889.
In this manner, ready to anticipate the repair professional to be active around 88.9% of the time.
To know more about probability refer to this :
https://brainly.com/question/24756209
#SPJ4
assume the population is right-skewed. experiment with various sample sizes of your choosing. what happens to the shape of the sample as the sample size increases? group of answer choices the sample becomes more and more like the population distribution. sample size does not impact the sample's shape. the sample becomes more and more normal. the spread of the sample increases.
Answers
The shape of the sample as the sample size increases is the sample becomes more and more like the population distribution
The Normal Distribution:A given set a data is considered to be normally distributed if it appears to take on a bell-shaped, symmetrical curve. Both skew (i.e. a lack of symmetry) and kurtosis (i.e. a more dramatically flattened or peaked curve) can be present in a distribution. If skew or kurtosis is present in a set of data, it cannot be said to be normally distributed.
A positively skewed (or right-skewed) distribution is a type of distribution in which most values are clustered around the left tail of the distribution while the right tail of the distribution is longer. The positively skewed distribution is the direct opposite of the negatively skewed distribution.
Learn more about Right - skewed at:
https://brainly.com/question/30006849
#SPJ4
At $15 per square foot, the cost of installing flooring in a room with these dimensions a.$121.50 b.$1215.00 c.$1290.00 d.$81
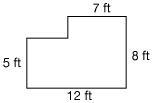
Answers
Answer:
b. $1215.00
Step-by-step explanation:
The area of the room can be figured any of several ways. One easy way is to figure the area of the enclosing 8 ft by 12 ft rectangle, then subtract area of the 3 ft by 5 ft cutout at upper left.
A = (8 ft)(12 ft) - (3 ft)(5 ft) = (96 -15) ft^2 = 81 ft^2
At a cost of $15 for each square foot, the installed flooring will cost ...
($15 /ft^2)(81 ft^2) = $(15·81) = $1215
Which triangle is not similar to the other two triangles?

Answers
Answer:
First choice top-down
Step-by-step explanation:
The Similarity Theorem Side-Angle-Side it can be checked here to see what triangles are similar.
All 3 triangles have 2 congruent sides so the triangles are all isosceles.
The base angles of isosceles triangles are congruent so knowing this and that the sum of angles in a triangle is 180° we can calculate the measure of all angles.
180-20 = 160; 160/2 = 80°
180-30 = 150; 150/2 = 75°
Now we can conclude that Δ JLK is not similar with Δ MNO ≈ ΔPRQ

in the expression 4x + (2x - 9) - 1/2x there are ___ term(s), ____ constant(s) and ____ coefficient(s).
Answers
Answer:
4 terms, 1 constant, 3 coefficients.
Step-by-step explanation:
Concept 9.7: Write the equation of the circle with center at (-7, 11) and radius of 8.

Answers
if it wants the measurement of arcJK....
Answer:
ArcJK= 128
Step-by-step explanation:
Circle is 360 degrees
<KL is the diameter which is a straight line equals 180 degrees
Since <KLis also a central angle arcKL equals 180
Take <K (26) and times by two cause its an inscribe angle, 26*2=52
arcJL=52
add both arcKL and arcJL together: 180+52=232
then you take 360-232=128
and 128 is KLarc
A company that recently changed it slogan is hosting an optional big company picnic.Some members of the marketing team are eating together at the picnic and sharing their thoughts on the new slogan. they find that 80% of them like the new slogan. for which population is 80% a legitimate estimate of the percent of employees who like the new slogan?
Answers
Answer:
Only those members of the marketing team eating together at the picnic
Step-by-step explanation:
The members of the marketing team eating together at the picnic weren't randomly selected from a larger population. They may not be representative of employees (marketing team or not) beyond their group.
Only members of the marketing team eating together depicts a 80 percent legitimate estimate of the percent of employees who like the new slogan.
What is an Estimate?This can be defined as the approximate calculation of a set of data or values.
The members of the marketing team eating together will represent 80 percent legitimate estimate because they weren't randomly selected from a larger population.
Read more about Estimates here https://brainly.com/question/24592593
Discrete Math
a.) How many permutations of { rho , χ , π , δ , ω } begin with the Greek letter δ ?
b.) Determine the number of 3-permutations of a set of cardinality eight.
Answers
To determine the number of permutations that begin with the Greek letter δ, we need to fix δ in the first position and consider the remaining four elements {rho, χ, π, ω} as a set.
The number of permutations of these four elements can be calculated as 4!, which is equal to 24. Therefore, there are 24 permutations that begin with the Greek letter δ.
To find the number of 3-permutations of a set with eight elements, we can use the formula for permutations of n objects taken r at a time, which is given by P(n, r) = n! / (n - r)!. In this case, we have eight elements in the set, and we want to find the number of 3-permutations, so r is equal to 3. Substituting these values into the formula, we get P(8, 3) = 8! / (8 - 3)! = 8! / 5! = (8 * 7 * 6) = 336. Therefore, there are 336 different 3-permutations of a set with eight elements.
a.) To calculate the number of permutations that begin with the Greek letter δ, we consider δ as a fixed element in the first position. This means that we only need to find the number of permutations of the remaining four elements {rho, χ, π, ω}. Since each of these four elements can occupy any of the remaining four positions, there are 4 choices for the second position, 3 choices for the third position, 2 choices for the fourth position, and 1 choice for the fifth position. Therefore, the total number of permutations is obtained by multiplying these choices together, giving us 4! = 4 * 3 * 2 * 1 = 24.
b.) To determine the number of 3-permutations of a set with eight elements, we can use the formula for permutations. The formula P(n, r) = n! / (n - r)! calculates the number of permutations of n objects taken r at a time. In this case, we have eight elements in the set, and we want to find the number of 3-permutations, so r is equal to 3. Plugging these values into the formula, we get P(8, 3) = 8! / (8 - 3)! = 8! / 5!. This simplifies to (8 * 7 * 6) / (3 * 2 * 1) = 336. Therefore, there are 336 different 3-permutations of a set with eight elements.
Learn more about permutations here: brainly.com/question/29855401
#SPJ11
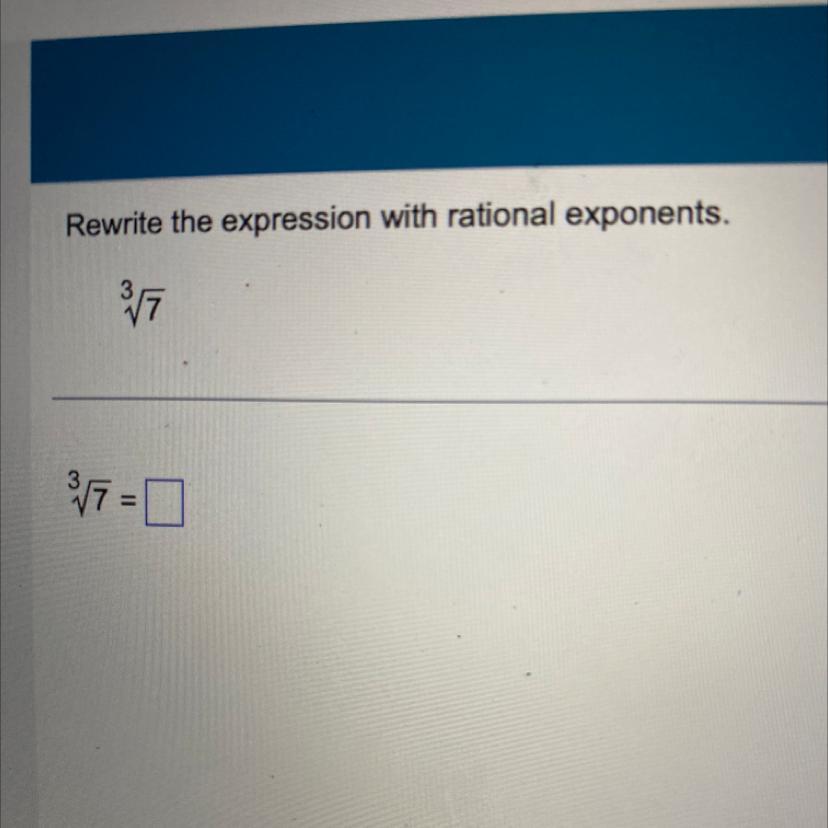
Rewrite the expression with rational exponents.
Answers
\(7^{(1/3)}\) is the equivalent expression to ∛7 with rational exponents.
What are rational exponents?
Rational exponents are exponents that are expressed as fractions. Specifically, a rational exponent of the form m/n is equivalent to taking the nth root of a number and then raising it to the power of m.
When we talk about rational exponents, we are referring to exponents that are written as fractions. Specifically, a rational exponent of the form m/n is equivalent to taking the nth root of a number and then raising it to the power of m.
So, in the case of ∛7, we can rewrite the cube root symbol (∛) as a rational exponent with a denominator of 3. That is, ∛7 can be expressed as \(7^{(1/3)}\) , where the 1/3 exponent means "take the cube root of 7".
Therefore, \(7^{(1/3)}\) is the equivalent expression to ∛7 with rational exponents.
To learn more about rationlal exponents from the given link:
https://brainly.com/question/3009444
#SPJ1
The graph shows the amount of gas in the tank of Bill's car during a trip to his mom's house. At one point he stopped for gas. About how mush
gas did Bill put in his tank when he stopped?
O 7 gallons
O 12 gallons
O 1 gallon
O 5 gallons

Answers
He had 7 in the tank when he filled it up, and it went to 12. So he added 5 gallons.
Sabia and arlan bougth 45 book for r 30 each old all ok them at the rote of 24 find the different the money pent and return
Answers
If Sabia and Arlan bought 45 books for rs 30, then at the rate of rs 24, they can buy 34 books.
What is an arithmetic operation?It is defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has basic four operators that are +, -, ×, and ÷.
It is given that, Sabia and Arlan bought 45 books for rs 30, then at the rate of rs 24, how many books they can buy,
Rs 30 = 45 book
Rs 30 = 45
Rs 1 = 45 / 30
Rs 24 = 3/2 × 24
Rs 24 = 34 books
Thus, if Sabia and Arlan bought 45 books for rs 30, then at the rate of rs 24, they can buy 34 books.
Learn more about the arithmetic operation here:
brainly.com/question/20595275
#SPJ1
Find the solution to the initial value problem. z (x)+z(x) 5e4x z(0)= 0, z'(0)= 0 The solution is z(x) =|-
Answers
The complete solution to the initial value problem, \(z"(x) + z(x) = 5e^{-4x}\), with initial conditions, \(z(0) = 0,\) \(z'(0)= 0\) is equals to \(z(x) = (-\frac{5}{17} )cosx + (\frac{20}{17} ) sinx + (\frac{5}{17} )e^{-4x} .\)
Initial value problem is a differential equation defined with enough additional conditions to specify the constants of integration that appear in the general solution and these conditions are called initial conditions. We have an initial value problem, \(z"(x) + z(x) = 5e^{-4x}\) , --(1) with initial conditions \(z(0) = 0, z'(0)= 0\). The homogeneous equation,\(z"(x) + z(x) = 0\) has auxiliary equation, \(m^{2} + 1 = 0\)
\(= > m^{2} = -1\)
\(= > m=\)±\(\sqrt{-1} =\)±\(i\)
so, general solution of equation (1) is \(z(x) = C_{1} cosx + C_{2} sinx\)
For particular solution, we use method of undetermined cofficient. Let \(z(x) = Ae^{-4x} }\)--(2)
differentiating equation (2), w.r.t x
\(z'(x) = \frac{d}{dx} ( Ae^{-4x} )\)
\(= > z'(x) = A\frac{d}{dx} (e^{-4x} ) =-4 A e^{-4x}\)
Again differentiating the above equation,
\(z"(x) = \frac{d}{dx} (-4A e^{-4x} )\)
\(= > z"(x) =-4 A( \frac{d}{dx} e^{-4x} ) = > z"(x) = -4A(-4)e^{-4x} = 16Ae^{-4x}\)
From (1), \(z"(x) + z(x) = 5e^{-4x}\)
\(= > 16Ae^{-4x} + A e^{-4x} = 5e^{-4x} = > e^{-4x} ( 16A + A ) = 5e^{-4x} = > 17A = 5\)
\(= > A = \frac{5}{17}\)
so, particular solution is \(z_{p} = (5/17)e^{-4x}\). As we know, complete solution is sum of general solution and particular solution, so complete solution of equation is,\(z(x) =C_{1} cosx + C_{2} sinx + (\frac{5}{17} )e^{-4x}\) --(*)
Now, using the initial conditions, \(z(0) = 0\)
\(= > 0 = C_{1} cos(0) + C_{2} sin(0) + (\frac{5}{17} )e^{-40}\)
\(= > 0 = C_{1} + (\frac{5}{17} ) ( since, cos(0) = 1, sin(0) = 0,e^{0} = 1)\)
\(= > C_{1} =\frac{5}{17}\)
\(z(x) = (\frac{-5}{17} )cosx + C_{2} sinx + (\frac{5}{17} )e^{-4x}\)
differentiating,\(z'(x)= (-\frac{5}{17} )(-sinx) - 4(\frac{5}{17})e^{-4x} + C_{2} cosx\)
Also,\(z'(0)= 0\)
\(= > 0 = (-\frac{5}{17} )(-sin(0)) - 4(\frac{5}{17} )e^{-40} + C_{2} cos(0)\)
\(= > 0 =( - \frac{20}{17} ) + C_{2}\)
\(= > C_{2} = \frac{20}{17}\)
Hence, the required solution of equation (1), is written as \(z(x) = (-\frac{5}{17} )cosx + (\frac{20}{17} ) sinx + (\frac{5}{17} )e^{-4x} .\)
For more information about initial value problem, visit :
https://brainly.com/question/19427862
#SPJ4
Complete question:
Find the solution to the initial value problem, \(z"(x) + z(x) = 5e^{-4x}\), \(z(0) = 0, z'(0)= 0. The solution is z(x) = ?\)
Which sequence is arithmetic?

Answers
True or False: for a sample with a standard deviation of s = 8, a score of x = 42 corresponds to z = –0.25. the mean for the sample is m = 40.
Answers
The given statement "For a sample with a standard deviation of s = 8, a score of x = 42 corresponds to z = -0.25. The mean for the sample is m = 40." is False because the calculated z-score does not match the given value.
To calculate the z-score, we use the formula z = (x - m) / s, where x is the score, m is the mean, and s is the standard deviation. Substituting the given values, we have z = (42 - 40) / 8 = 0.25. However, the given statement states that the z-score is -0.25, which is incorrect. Therefore, the statement is false.
The correct z-score for x = 42 with a mean of m = 40 and standard deviation of s = 8 is 0.25, not -0.25.
For more questions like Z-score click the link below:
https://brainly.com/question/15016913
#SPJ11
does the function f (x )equals begin display style fraction numerator x squared minus 9 over denominator x minus 3 end fraction end style have a vertical asymptote at x equals 3? select the answer that best answers the question and describes the reasoning. no. since limit as x rightwards arrow 3 of f (x )equals 6, f (x )will have a hole at x equals 3 and not a vertical asymptote. we can't tell whether or not there is a vertical asymptote by just looking at the function. since the denominator is 0 when x equals 3, there is a vertical asymptote at x equals 3. since the numerator is 0 when x equals 3, there is a vertical asymptote at x equals 3.
Answers
No. Since the limit as x approaches 3 from both sides of f(x) equals 6, f(x) will have a hole at x equals 3 and not a vertical asymptote.
A vertical asymptote is a vertical line on a graph that the function approaches but never touches as the input values approach a certain value. In other words, it is a value of the independent variable for which the function approaches infinity or negative infinity as the independent variable approaches that value.
It is often found in rational functions, where the denominator becomes zero at some value, causing the function to become undefined at that point.
Visit here to learn more about vertical asymptote brainly.com/question/29260395
#SPJ11
Match the positive or negative number on the right with a situation that represents it on the left.
An increase in altitude of 6 miles.
6 degrees below zero.
Taking 12 steps back.
Going up 12 stairs.
Depositing $2,000
A withdrawal of $2,000
DRAG & DROP THE ANSWER
−6-6−6
+12+12+12
+6+6+6
+2,000+2,000+2,000
−12-12−12
−2,000-2,000−2,000
Answers
The correct matching of positive and negative number according to the situation is given by,
An increase in altitude of 6 miles.→ +6
6 degrees below zero.→-6
Taking 12 steps back.→-12
Going up 12 stairs.→+12
Depositing $2,000 →+2000
A withdrawal of $2,000→ -2000.
The left hand side statement representing the situation of right hand side are as follow,
An increase in altitude of 6 miles represents the positive value of 6 as it increases.
+ 6.
6 degrees below zero represents the negative value of 6 as below zero numbers are negative.
-6.
Taking 12 steps back represents the negative value of 12 as moving back is negative direction.
-12.
Going up 12 stairs represents the positive value of 12 as moving up is always positive.
+12.
Depositing $2,000 represents the positive value of 2000 as it increases the amount.
+2000
A withdrawal of $2,000 represents the negative value of 2000 as it decreases the amount.
-2000.
learn more about negative number here
brainly.com/question/19983612
#SPJ1