A hair stylist knows that 87% of her customers get a haircut and 40% get their hair colored on a regular basis. Of the customers who get their hair cut, 24% also get their hair colored. What is the probability that a randomly selected customer gets their hair cut and colored?
0.10
0.21
0.35
0.40
Answers
Answer:
Okay so!
Step-by-step explanation:
for a cut that's .87 and for a color that is .24 so you multiply them together to get the probability for the color which is
.35 or C on edge
The probability that a randomly selected customer gets their hair cut and colored is .
What is probability?Probability is the chance of happening an incident or event. A probability is calculated by the ratio of the possible outcomes to total number of outcomes.
Given, the probability of he customer get a hair cut is = P(A) = 87% = 0.87.
The probability of he customer get their hair colored is = P(B) = 40% = 0.4.
Therefore, the probability of a randomly selected customer get hair cut and hair color is = P(A) × P(B) = 0.87 × 0.4 = 0.35
Therefore, 35% of the total customer get hair cut and color.
Learn more about probability here: https://brainly.com/question/13700963
#SPJ2
Related Questions
5. Oshaunda buys a car that costs $21,000. It depreciates at 8.2% per year. a. Write an equation for the value of the car. V=21,000(1-0.082) V-21,000(0.918) B. Oshaunda tries to sell the car 4 years later. What is the car worth when it is 4 years old? Hint: Use your formula for part (a), and plug in t = 4. Use GEMA to finish the math.
Answers
Answer:
a.
\(f(t) = 21000( {.918}^{t} )\)
b.
\(f(4) = 21000( {.918}^{4}) = 14913.86\)
Wyatt mows lawns to earn money. He charges by the area
of the yard. A new customer has a yard in the shape of a
triangle with a base of 200 feet and a height of 70 feet.
What is the area of the yard?
4,667 ft?
540 ft?
7,000 ft
270 ft?
Answers
area of triangle formula=1/2*base*height
The area of the triangular yard is 7000 ft².
What is the area of a triangle?The entire area enclosed by three sides of a triangle is the area of it.
Given,
The base of the triangle is 200 feet and the height of the triangle is 70 feet.
Therefore, the area of the triangle
= (1/2) × base of the triangle × height of the triangle = (1/2) × 200 × 70 ft² = 7000 ft².
Learn more about the area of a triangle here: https://brainly.com/question/22625791
#Tag #SPJ2
Hopefully you guys don’t solve this wrong. I got 3 problems wrong on my homework yesterday.

Answers
Solution
The measure of the angle
Alternate interior angles are "interior" (between the parallel lines), and they "alternate" sides of the transversal. Notice that they are not adjacent angles (next to one another sharing a vertex).
When the lines are parallel,
the alternate interior angles
are equal in measure.
Hence the angle in a parallel lines are said to be corresponding and equal
Therefore the measure of the angle 139°

which system of inequalities is represented on this graph? NEED THIS ASAP picture below

Answers
a movie theater decreased the size of its popcorn bags by 20 percent if the old bags held 15 cups of popcorn how much do the new bags hold
Answers
Answer:
12 cups
Step-by-step explanation
If the size of the bag decreased by 20%, so will the number of cups held.
Number of cups held before the change = 15 cups
If the number of cups held after the 20% reduction in the size of the bag
= (100 - 20)% × 15
=80% × 15
= 12 cups
The new bags will hold 12 cups.
Find the area of the figure

Answers
Answer:
C. 418 cm²
Step-by-step explanation:
Rectangle
= s × s
= 19 × 19
= 361 cm²
Triangle
= 1/2 × 6 × 19
= 57 cm²
361 + 57 = 418 cm²
So, therefore your answer is 418 cm²
Solve the problem by multiplying first.
Jamian bought a total of 35 bagels and donuts for a morning meeting. He paid a total of
$25.75. Each donut cost $0.55 and each bagel cost $1.20. The system of equations
b + d = 35
1.200 + 0.55d = 25.75 models this situation, where b is the number of bagels and d
is the number of donuts. How many of each did Jamian buy?
{ 1.200
Jamian bought
bagels and
donuts.
Answers
Answer:
Number of bagels = 10
Number of donuts = 25
Step-by-step explanation:
Let Number of bagels = b
Number of donuts = d
As given,
Each donut cost $0.55 and each bagel cost $1.20
⇒ Cost of d donuts = $0.55d
Cost of b bagels = $1.20b
Also given,
Jamian bought a total of 35 bagels and donuts
⇒ b + d = 35 ........(1)
Also,
He paid a total of $25.75.
⇒ 1.20b + 0.55d = 25.75 .........(2)
Now,
Multiply equation (1) by 1.20 , we get
1.20( b + d = 35 )
⇒1.20b + 1.20d = 42 ..........(3)
Now,
Subtract equation (2) from equation (3), we get
1.20b + 1.20d - ( 1.20b + 0.55d ) = 42 - 25.75
⇒1.20b + 1.20d - 1.20b - 0.55d = 16.25
⇒0.65d = 16.25
⇒d = \(\frac{16.25}{0.65}\) = 25
⇒d = 25
Put the value of d in equation (1) , we get
b + d = 35
⇒b + 25 = 35
⇒b = 35 - 25 = 10
⇒b = 10
∴ we get
Number of bagels = b = 10
Number of donuts = d = 25
Taura paid $64 for 4 tickets to a baseball game. At that rate, how much would it cost Victor to buy 6 tickets?
A.
$96
B.
$10
C.
$80
D.
$16
Answers
Answer:
A
Step-by-step explanation:
I hope this helps you out!
Explain the steps when solving for the variable y
12x+2y=18
Answers
Answer:
Simplifying
12x + 2y = 18
Solving
12x + 2y = 18
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-2y' to each side of the equation.
12x + 2y + -2y = 18 + -2y
Combine like terms: 2y + -2y = 0
12x + 0 = 18 + -2y
12x = 18 + -2y
Divide each side by '12'.
x = 1.5 + -0.1666666667y
Simplifying
x = 1.5 + -0.1666666667y
Answer:
Hi
Step-by-step explanation:
First, you need to subtract both sides by 12x
12x+ 2y=18
-12x -12x
That will give you: 2y= 18-12x
Next, you need to deviede both sides by 2
2y/2= 18-12x/2
That gives you the answer:
y= 18-6x
(im not 100% sure but i think this is right, feel free to correct me)
• PQ²+PR²=QR²
• PQ²+QR²=PR²
• PR²- PQ²=QR²
• PR²- QR²=PQ²

Answers
Answer:
Option A
\( {pq}^{2} + {pr}^{2} = {qr}^{2} \)
Step-by-step explanation:
This is because here,
PQ is the Height of the right triangle.
QR is the Base of the right triangle.
PR is the Hypotenuse of the right triangle.
So, as according to Pythagoras Theorem,
\( {base}^{2} + {height}^{2} = {hypotenuse}^{2} \)
Also,
\( {pq}^{2} + {qr}^{2} = {pr}^{2} \)
Not,
\({pq}^{2} + {pr}^{2} = {qr}^{2} \)
Hence, Option A is not correct.
What is the probability that either event will occur?
15
A
17
B
2
P(A or B) = P(A) + P(B)
P(A or B) = [?]
Answers
The probability that either event will occur is 0.83
What is the probability that either event will occur?From the question, we have the following parameters that can be used in our computation:
Event A = 18
Event B = 12
Other Events = 6
Using the above as a guide, we have the following:
Total = A + B + C
So, we have
Total = 18 + 12 + 6
Evaluate
Total = 36
So, we have
P(A) = 18/36
P(B) = 12/36
For either events, we have
P(A or B) = 30/36 = 0.83
Hence, the probability that either event will occur is 0.83
Read more about probability at
brainly.com/question/251701
#SPJ1
![What is the probability that either event will occur?15A17B2P(A or B) = P(A) + P(B)P(A or B) = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/5dd7e3IsxzB7UDoPS50kjKaWnZ2gZOhz.jpeg)
a house is located 6 miles north of the center of the town and is to the east of the cell tower. if the house lies on the boundary of the cell tower's coverage, how far east of the center of the town is the house?
Answers
The house is 0 miles east of the center of the town.
To determine how far east of the center of the town the house is located, we need more information about the shape of the cell tower's coverage. However, we can make an estimation based on the given information.
Since the house lies on the boundary of the cell tower's coverage, we can assume that the cell tower's coverage area is circular.
Let's consider the following scenario: if the center of the town is the origin of a coordinate system, and the cell tower is located at (0,0), with the house 6 miles north of the town's center, we can represent the house's location as (0,6).
Assuming the cell tower's coverage area is circular, the house must lie on the circumference of this circle. In this case, the radius of the circle is 6 miles (since the house is located 6 miles north of the town's center).
Now, if we want to find the eastward distance of the house from the center of the town, we need to find the x-coordinate of the house. Since the house is directly east of the cell tower, the x-coordinate will be 0.
For more such questions on center
https://brainly.com/question/28322552
#SPJ8
In a math class with 28 students, a test was given the same day that an assignment
was due. There were 18 students who passed the test and 23 students who completed
the assignment. There were 16 students who passed the test and also completed the
assignment. What is the probability that a student who passed the test did not
complete the homework?
Answers
Answer:
Probability that a student who passed the test did not complete the homework = 0.07
Step-by-step explanation:
Given:
Total number of students = 28
Number of students who passed the test = 18
Number of students who completed the assignment = 23
Number of students who passed the test and also completed the assignment = 16
To find: probability that a student who passed the test did not complete the homework
Solution:
Probability refers to chances of occurrence of some event.
Probability = number of favorable outcomes/total number of outcomes
Let A denotes the event that students passed the test and B denotes the event that students completed the assignment
P(A only) = \(P(A)-P(A\cap B)\)
Here,
\(P(A)=\frac{18}{28}\,,\,P(A\cap B)=\frac{16}{28}\)
So,
\(P(A\,\,only)=\frac{18}{28}-\frac{16}{28}=\frac{2}{28}=\frac{1}{14}=0.07\)
Therefore,
probability that a student who passed the test did not complete the homework = 0.07
Answer:
2/9
Step-by-step explanation:
Can anyone help me with this math test please i gotta have everything turned in by midnight tn!! I need fast answers asap!! Heres another one of the questions on it!!

Answers
Answer:
D
Step-by-step explanation:
cause 2/3 of 6 is 4
and 1/2 of 4 is 2
I need help with 15, 16, 17, and 18 please

Answers
Answer:
y = 2x + 2
Explanation:
We can use the following equation to write an equation in slope-intercept form.
\(y-y_1=m(x-x_1)\)Where (x1, y1) is a point in the line and m is the slope. Additionally, the slope can be calculated as:
\(m=\frac{y_2-y_1}{x_2-x_1}\)Where (x2, y2) is another point in the line.
So, replacing (x1, y1) by (0, 2) and (x2, y2) by (3, 8), we get that the slope is equal to:
\(m=\frac{8-2}{3-0}=\frac{6}{3}=2\)Finally, replacing m by 2 and (x1, y1) by (0, 2), we get:
\(\begin{gathered} y-2=2(x-0) \\ y-2=2x \\ y-2+2=2x+2 \\ y=2x+2 \end{gathered}\)Therefore, the equation in slope-intercept form is:
y = 2x + 2
*£ HELP PLS !! URGENT!! AFFECT MY GRADE!! *Problem 5.3
Here are three lines that intersect at
one point.
Laila wrote the equation
x + 18 = 90.
Describe the error that Laila might
have made.

Answers
Answer:
Laila assumed that the lines that formed the angles x and 18° added up to 90. This is in fact false because of the lack of the square marking to signify it as a right or 90 degree angle.
The marginal cost of a product is modeled by 16 16x + 5 dC dx C = = 3 where x is the number of units. When x = 17, C = 140. (a) Find the cost function. (Round your constant term to two decimal places.) (b) Find the cost (in dollars) of producing 40 units. (Round your answer to two decimal places.) $
Answers
We can substitute the value of x = 40 into the cost function and solve for C. Thus;C = (-8/5)(40)^2 - (13/5)(40) + 579.60C = -1280 - 104 + 579.60C = 455.60The cost (in dollars) of producing 40 units, rounded to two decimal places is $455.60. Therefore, option (d) is correct.
(a) Solution:We are given the marginal cost of a product which is modeled by;
16 + 16x + 5(dC/dx) C
= 3
We know that the marginal cost of a product is the derivative of the cost function;Thus, we have;
dC/dx
= 16 + 16x + 5(dC/dx) C
= 3
Rearranging the above equation gives us;
5(dC/dx)
= 3 - 16x - 16
Now;5(dC/dx)
= -16x - 13
Dividing by 5 on both sides, we have;
dC/dx
= (-16/5)x - (13/5)
Integrating with respect to x, we have;
C
= (-16/10)x^2 - (13/5)x + k
where k is a constant. We are given that when x
= 17, C
= 140. Thus;140
= (-16/10)(17)^2 - (13/5)(17) + k140
= -486.2 + 46.6 + kk
= 579.6
Thus the cost function is;C
= (-8/5)x^2 - (13/5)x + 579.6
The constant term rounded to two decimal places is 579.60Therefore, the cost function is given by C
= (-8/5)x^2 - (13/5)x + 579.60
(b) Solution:We are required to find the cost (in dollars) of producing 40 units, given that the cost function is;C
= (-8/5)x^2 - (13/5)x + 579.60
.We can substitute the value of x
= 40 into the cost function and solve for C. Thus;C
= (-8/5)(40)^2 - (13/5)(40) + 579.60C
= -1280 - 104 + 579.60C
= 455.60
The cost (in dollars) of producing 40 units, rounded to two decimal places is $455.60. Therefore, option (d) is correct.
To know more about substitute visit:
https://brainly.com/question/29383142
#SPJ11
(Trig word problems)
From a hot-air balloon, Enola measures a 22° angle of depression to a landmark that’s 310 feet away, measuring horizontally. What’s the balloon’s vertical distance above the ground? Round your answer to the nearest hundredth of a foot if necessary.
Answers
Step-by-step explanation:
See image

Which is the graph of y = - root(7, x) - 8 ?





Answers
Answer:
Step-by-step explanation:

Suppose the lifetime in months of an engine, working under hazardous conditions, has a Gamma distribution with a mean of 2 months and a variance of 4 months squared. (a) Determine the median lifetime of an engine. (b) Suppose such an engine is termed successful if its lifetime exceeds 10 months. In a sample of 10 engines, determine the probability of at least 2 successful engines
Answers
(a) The median lifetime of an engine is approximately 2.772 months, which is the value that divides the distribution into two equal halves.
b) The probability of having at least 2 successful engines in a sample of 10 engines is approximately 0.98168, or about 98.17%.
(a) To determine the median lifetime of an engine, we need to find the value of the random variable that divides the distribution into two equal halves.
The Gamma distribution is defined by two parameters: shape (k) and scale (θ). The mean and variance of a Gamma distribution are given by:
Mean = k * θ
Variance = k * θ^2
Given that the mean is 2 months and the variance is 4 months squared, we can equate these values to the corresponding formulas:
2 = k * θ
4 = k * θ^2
We can solve these equations simultaneously to find the values of k and θ:
Dividing the second equation by the first equation, we get:
4/2 = θ/θ^2
2 = 1/θ
θ = 1/2
Substituting this value back into the first equation, we have:
2 = k * (1/2)
k = 4
Therefore, the parameters of the Gamma distribution are k = 4 and θ = 1/2.
To find the median lifetime, we need to solve for the value of x such that the cumulative distribution function (CDF) of the Gamma distribution equals 0.5:
CDF(x) = 0.5
Using a statistical software or tables for the Gamma distribution, we can find that the median lifetime of an engine is approximately 2.772 months.
(b) The probability of at least 2 successful engines in a sample of 10 engines can be calculated using the cumulative distribution function (CDF) of the Gamma distribution. We need to find the probability of getting 2 or more engines with a lifetime exceeding 10 months.
Let X be the number of successful engines in a sample of 10. Since the lifetime of an engine is a continuous random variable, we need to use the cumulative distribution function for X.
P(X ≥ 2) = 1 - P(X < 2)
Using the properties of the Gamma distribution, we can calculate this probability:
P(X < 2) = P(X = 0) + P(X = 1)
The probability mass function (PMF) of the Gamma distribution is given by:
P(X = x) = (k^x * exp(-k)) / (x!)
For x = 0:
P(X = 0) = (4^0 * exp(-4)) / (0!) = exp(-4)
For x = 1:P(X = 1) = (4^1 * exp(-4)) / (1!) = 4 * exp(-4)
Therefore:
P(X < 2) = exp(-4) + 4 * exp(-4) ≈ 0.01832
Finally, we can calculate the probability of at least 2 successful engines:
P(X ≥ 2) = 1 - P(X < 2) = 1 - 0.01832 ≈ 0.98168
Therefore, the probability of at least 2 successful engines in a sample of 10 engines is approximately 0.98168, or about 98.17%.
For more question on median visit:
https://brainly.com/question/26177250
#SPJ8
Steve built a square hamster pen that has a perimeter of 240 centimeters.
Answers
Answer:
What's the question?
Step-by-step explanation:
Answer: I also need answer for this question
Step-by-step explanation:
Any body got
Keeping in mind that a function’s rate of change is a measure of how fast the function is increasing or decreasing, what does the slope of a linear function indicate?
Answers
Answer:
Required Answer:-The function shows negative
No links please.....

Answers
Answer:
the circumference is 2.25675833π
simplify how you want
Step-by-step explanation:
Describe the error Sadie made, and explain how to find the correct answer. (Refer to image)
Step 1: Explain the error made
Step 2: Explain how to find the correct answer.
Answers
a)Error:multiplied the numerator and denominator by 3 instead of 2.
b)The correct answer to the given expression is 8/15.
In the given image, Sadie made an error in the simplification of the expression.
The error is that she multiplied the numerator and denominator by 3 instead of 2.
She simplified the numerator and the denominator before carrying out multiplication by 2.
This resulted in the final answer being incorrect.
The correct answer would be 8/5.
The correct way to simplify the expression is as follows:
\($$\frac{4}{3} \div \frac{5}{6} = \frac{4}{3} \times \frac{6}{5}$$\)
Now, cross-cancelling can be performed because the numerator of the first fraction and the denominator of the second fraction have a common factor of 2.
\($$=\frac{4 \times 2}{3 \times 5} = \frac{8}{15}$$\)
Therefore, the correct answer to the given expression is 8/15.
To know more about expression, visit:
brainly.com/question/17621214
#SPJ11
2
(
3
r
+
4
)
−
3
(
r
+
1
)
=
11
Answers
Hey there!
ASSUMING
2(3r + 4) - 3 (r + 1) = 11
IF SO
2(3r + 4) - 3 (r + 1) = 11
2(3r + 4) - 3 (1r + 1) = 11
DISTRIBUTE
2(3r) + 2(4) - 3(1r) - 1(1) = 11
6r + 8 - 3r - 1 = 11
COMBINE the LIKE TERMS
(6r - 3r) + (8 - 3) = 11
6r - 3r + 8 - 3 = 11
3r + 5 = 11
SUBTRACT 5 to BOTH SIDES
3r + 5 - 5 = 11 - 5
SIMPLIFY!
3r = 11 - 5
3r = 6
DIVIDE 3 to BOTH SIDES
3r/3 = 6/3
SIMPLIFY!
r = 6/3
r = 2
Therefore, the answer should be: r = 2
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
Weekly wages at a certain factory are normally distributed with a mean of $400 and a standard deviation of $50. Find the probability that a worker selected at random makes between $350 and $400. ?%
Answers
The probability that a worker selected at random makes between $350 and $400 is given as follows:
0.34 = 34%.
How to obtain a probability using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation for the salaries in this problem are given as follows:
\(\mu = 400, \sigma = 50\)
The probability that a worker selected at random makes between $350 and $400 is the p-value of Z when X = 400 subtracted by the p-value of Z when X = 350, hence:
X = 400:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (400 - 400)/50
Z = 0
Z = 0 has a p-value of 0.5.
X = 350:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (350 - 400)/50
Z = -1
Z = -1 has a p-value of 0.16.
Hence the probability is given as follows:
0.5 - 0.16 = 0.34 = 34%.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
x^3+x^2-10x+8 divided by x+4
please also explain the steps
Answers
Answer:
Step-by-step explanation:
Okay, so assuming you have set up your division problem, you first have to find a value that will set x = to x^3. This value is x^2. So, put that above the division symbol. Next, multiply (x +4) by x^2. Then, subtract that answer from x^3 + x^2. You should get -3x^2 - 10x. Then, find a value to get x to -x^2. This value is -3x. So, put that above the division symbol. Multiply (x + 4) by -3x. Then, subtract that value from -3x^2 - 10x. You should get 2x + 8 as your answer. Now find a value to get x to 2x. 2 should work. So, put that above the division symbol. Multiply (x +4) by 2. When subtract your answer from 2x + 8 you get 0. Therefore, the answer is x^2 - 3x +2. Hope this helps!!
Find x, and GH.
X =
GH: =
34
7x + 6
4x + 8

Answers
By using given figure, x=9/4 and the length of GH = 21.75.
What is the length ?
Here, in given figure,
BG≈GF and CH≈HE
now by using these similarities, we can write as,
BG≈GF therfore, \(\frac{GF}{BG}\) = 1:1
\(\frac{GF}{BF}\)=\(\frac{4x+8}{34}\)
1/2=\(\frac{4x+8}{34}\)
8x+16=34
8x= 18
x=9/4
if x=9/4 then,
GH= 7x+6 = 7(9/4)+6 =63/4+6 =\(\frac{63+24}{4}\) = 21.75
What is similarity of sides?
similarity of sides refers to the property of two geometric shapes or figures having the same shape but not necessarily the same size. More specifically, two shapes are said to be similar if their corresponding angles are congruent and their corresponding sides are proportional in length.
To know more baout similarities, visit:
https://brainly.com/question/9753824
#SPJ1
What is the measure of the indicated central angle ? A. None of the above B. 20° C. 15° D. 10° E. 25°
Answers
Answer:
b
Step-by-step explanation:
Charlotte the turtle was born with 4 squares on her shell,
as in the first picture below. When she was 1 year old, 12
new squares appeared around the old squares, as in the
second picture below. Each year, a new group of squares
appeared around the old squares.
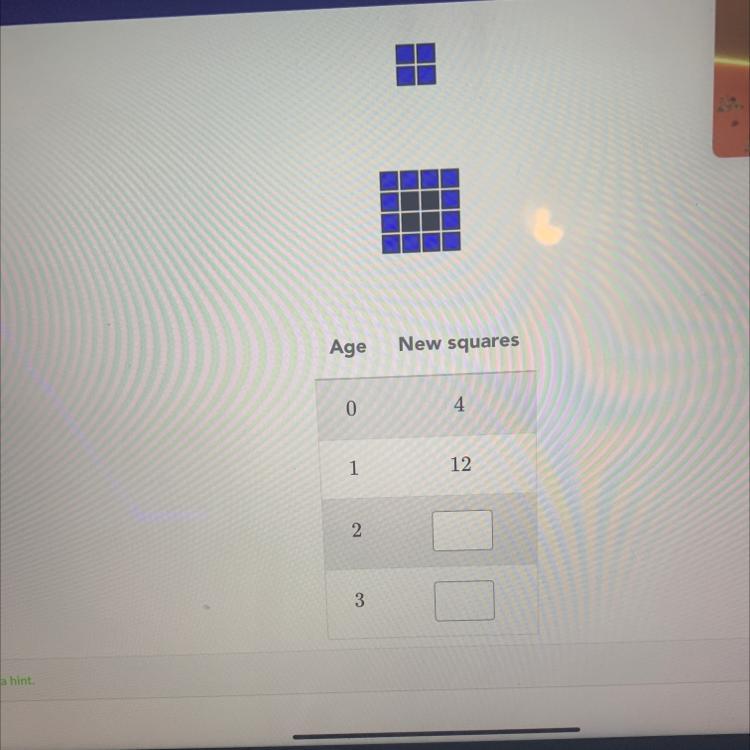
Answers
Answer:
Step-by-step explanation: