a healh Insurance plan cost is $150 each month plus an extra $25 for each doctors visit Which equation below models the total yearly cost see of the plan as a function of the number of doctors visits n
Answers
The function that represents the total yearly cost is =$1800 + $300n.
The total cost of the health insurance can be modelled as: fixed cost + (variable cost x number of doctor visits)
$150 + $25n
Fixed cost is the cost that is constant. It does not depend on any other factor. Variable cost is the cost that varies with the number of doctor visits. The higher the doctor visits, the higher the variable cost.
The yearly cost = 12 x ($150 + $25n)
= $1800 + $300n
To learn more about fixed cost, please check: https://brainly.com/question/25879561
Related Questions
Solve - x/6 less than or equal to 3
Answers
Answer: x is greater than or equal to 18
Step-by-step explanation:
Answer:
x ≤ - 2
Step-by-step explanation:
- x/6 ≤ 3
- x/2 ≤ 1
- x ≤ 2
x ≤ - 2
How do you find the probability of something.
Answers
Answer:
One divided by the
object given.
Please all the steps, one by one! How can this be solved?

Answers
There are 5 full square and 6 triangles that are half squares.
5 + (6)(1/2) = 5 + 3 = 8
You could also break this into smaller shapes (like a big triangle on the top and a smaller triangle and rectangle on the bottom and use area formulas to calculate the area. But counting works well in this example.


Answer: 8
Step-by-step explanation:
First you split up this shape into two different shapes, a triangle and trapezoid
Put a line through the coordinates (-2,2) to (-1,2); the top is a triangle and the other is a trapezoid
Area of the trapezoid is A = .5x (base1 + base2) x height
base1 of the trapezoid goes from -4 to -1 which is 3
base2 goes from -2 to -1 which is 1
height is 0 to 2 whcich is 2
A = .5 x (3+1) x 2 = 4
Now area of a triangle is A = .5 x base x height
the base goes from -2 to 2 which is 4
the height goes from 2 to 4 which is 2
A = .5 x (4) x (2) = 4
Area of the Trapezoid + Area of the Triangle = Total Area
4 + 4 = 8
Juanita is making a ribbon as shown 4 cm 15 cm 3 cm explain two different ways you can find the area of the ribbon then find the area of the ribbon

Answers
Answer:
6
Step-by-step explanation:
A=hbb/2=4·3/2=6
To find a triangle's area, use the formula area = 1/2 * base * height. Choose a side to use for the base, and find the height of the triangle from that base. Then, plug in the measurements you have for the base and height into the formula
or
The area of a triangle is the space enclosed within the three sides of a triangle. It is calculated with the help of various formulas depending on the type of triangle and is expressed in square units like, cm2, inches2, and so on.
It is Flame's birthday today.
She is 9 years older than Tyger.
Altogether, their ages add up to 23 years.
How old is Flame?
Answers
Answer:
she is 16
Step-by-step explanation:
16 -9=7
16+7= 23
Hope this helps.
uestion 1 (10 points)
The number of fish in a lake decreased by 25% between last year and this year. Last year there were 60 fish
in the lake. What is the population this year? If you get stuck, consider drawing a diagram.
В IU
SS
TU
1
Submit
O 07:3
Answers
Answer:
i think 45
Step-by-step explanation:
60 x .25 = 15
60-15 = 45
consider the curve given by the equation 3 y xy 2. it can be shown that 2 3 dy y dx y x . (a) write an equation for the line tangent to the curve at the point 1, 1 . (b) find the coordinates of all points on the curve at which the line tangent to the curve at that point is vertical. (c) evaluate 2 2 d y dx at the point on the curve where x 1 and y 1.
Answers
The equation for the line tangent to the curve at the point (1, 1) is y = 3x - 2.
(b) The line tangent to the curve at a point is vertical when the slope of the curve is zero. So, we can set the derivative of the curve equation equal to zero to find the x-coordinates of the points at which the line tangent to the curve is vertical.
2 3 dy y dx y x = 0
2 3(2x + y) = 0
2x + y = 0
x = - y/2
So, the x-coordinates of the points at which the line tangent to the curve is vertical are x = -y/2.
(c) We can evaluate 2 2 d y dx at the point (1, 1) by substituting x = 1 and y = 1 into the derivative of the curve equation.
2 3 dy y dx y x = 2 3(2(1) + 1) = 8/3
Learn more about line tangent here:
https://brainly.com/question/23265136
#SPJ4
i need help with this, its the same assignment but in two parts.


Answers
Answer:
I wish I could help but I`m not sure how to do tables
Answer:
True
Step-by-step explanation:
The answer is true because most people in the question were said to prefer more spicy things than sweeter things.
Have a fantabulous day!
Lilac~
A film begins at 21 25 and lasts for 100 minutes. At what time will it end? Express your answer using the 24- hour clock.
Answers
Answer:
23 05
Step-by-step explanation:
change 100 minutes to hours ,then add it to the starting time for the film.
Answer:
23 05
Step-by-step explanation:
from 21 25-22 00 35min are passed
and remain With 65min from 100min
from 22 00-23 00 60min are passed
and remain With 5min so then at 23 05 all 100min are passed from 21 25. thanks
A solid with surface area 50units^2 is dilated by a scale factor of K to obtain a solid surface area 200units^2. Find the value of K.
Answers
The value of K is 2.
Let's denote the scale factor as K. The surface area of a solid after dilation is directly proportional to the square of the scale factor.
We are given that the initial surface area of the solid is 50 units^2, and after dilation, the surface area becomes 200 units^2.
Using the formula for the surface area, we have:
Initial surface area * (scale factor)^2 = Final surface area
50 * K^2 = 200
Dividing both sides of the equation by 50:
K^2 = 200/50
K^2 = 4
Taking the square root of both sides:
K = √4
K = 2
Therefore, the value of K is 2.
for such more question on scale factor
https://brainly.com/question/3381225
#SPJ8
Neeeeeeeeeeeedddddddd hellllllllppppppppppp
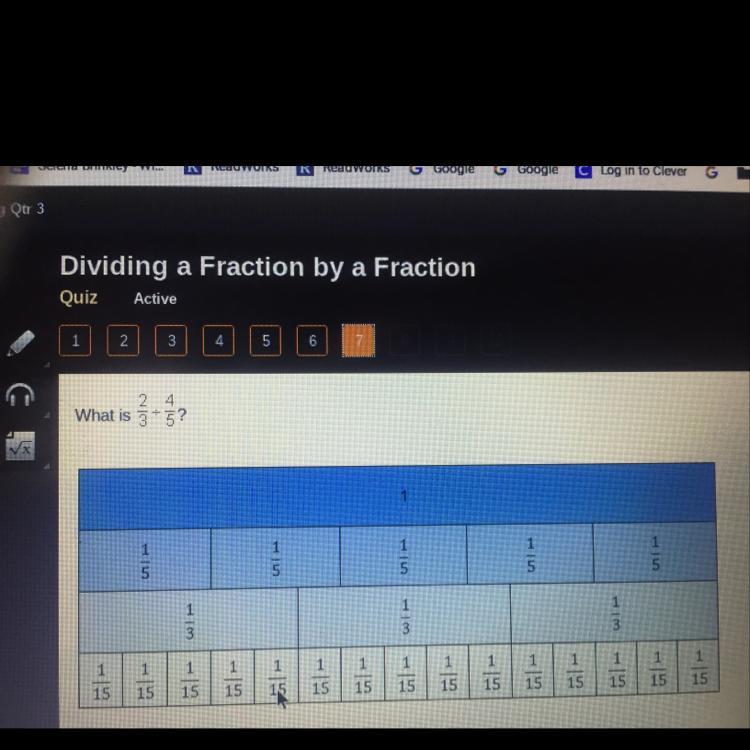
Answers
Answer:
0.8333333 which goes on forever
Step-by-step explanation:
45% of what number is 7.2
Answers
Hello!
45% of x = 7.2
45x/100 = 7.2
45x = 7.2 * 100
45x = 720
x = 720/45
x = 16
the number = 16
what is the value of x in the equation 2.5(6x-4)=10+4(1.5+0.5x)?
a. 1/3
b. 1/2
c. 2
d. 13

Answers
Answer:
x = 2
Step-by-step explanation:
Given
2.5(6x - 4) = 10 + 4(1.5 + 0.5x) ← distribute parenthesis on both sides
15x - 10 = 10 + 6 + 2x , that is
15x - 10 = 16 + 2x ( subtract 2x from both sides )
13x - 10 = 16 ( add 10 to both sides )
13x = 26 ( divide both sides by 13 )
x = 2
Answer:
2
Step-by-step explanation:
15x-10=10+6+2x
15x-2x=10+10+6
13x=26
divide 13 both sides
x=2
If the area of the rug in this den 48 square feet and the width of the carpet is 6’, what is the perimeter of the rug?
A. 112’
B. 28’
C. 8’
D. 108’
Answers
Answer:
B
Step-by-step explanation:
The perimeter of rug is 28 feet's.
We have a rug.
We have to determine its perimeter.
What is the Perimeter of a Rectangle ?The perimeter of rectangle will be -
P = 2(L + B)
According to the question -
Area = 48 square feet
Width = 6 feet
Then -
L x 6 = 48
L = 8 feet
Therefore, the perimeter will be -
2(L + B) = 2 x 14 = 28 feet's.
Hence, the perimeter of rug is 28 feet's.
To solve more questions on Rectangles, visit the link below-
https://brainly.com/question/20887416
#SPJ2
Identify the indicated parts of the figure below.

Answers
Answer:
The top one is a triangle which is the back part of the shape. The bottom left one is also a triangle and the bottom right one is a rectangle
What is the constant of variation for the quadratic variation?
7y = 0.28x²
A. 0.04
B. 0.28
C. 0.98
D. 7
Answers
Answer:
A.004
Step-by-step explanation:
I been Doing this for some Years And I knw it cuz I go on it EvenyDay
The common ratio of the geometric sequence -14,-84,-504
Answers
A common ratio is basically a ratio of next sequence and the sequence you want
To find a common ratio of geometric sequence, we usually define 'r' as common ratio.
\( \displaystyle \large \tt{r = \frac{next \: \: sequence}{the \: \: sequence \: \: you \: \: want} }\)
For example, I want to focus on -14 and the next sequence would be -84.
Hence,
\( \displaystyle \large{r = \frac{ - 84}{ - 14} }\)
Thus, r is 6 because both numerator and denominator are negative. negative divides negative = positive.
Or you want to choose -84, then the next sequence would be -504.
\( \displaystyle \large{r = \frac{ - 504}{ - 84} }\)
Then r would still be 6. Since both ways have r as 6 and this proves that the sequence is geometric.
Hence, the common ratio is 6.
(8 points) Find the maximum and minimum values of f(2,y) = 7c+y on the ellipse 2? +9y2 maximum value minimum value:
Answers
The maximum value of f(2,y) = 7c+y on the ellipse 2x^2 + 9y^2 = 1 is (7/√2) and the minimum value is (-7/3)√2.
To find the maximum and minimum values of f(2,y) = 7c+y on the ellipse 2? +9y2, we need to use Lagrange multipliers.
First, we write out the equation for the ellipse:
2x^2 + 9y^2 = 1
Next, we set up the Lagrange multiplier equation:
∇f = λ∇g
where f(2,y) = 7c+y and g(x,y) = 2x^2 + 9y^2 - 1.
Taking the partial derivatives, we get:
∂f/∂x = 0
∂f/∂y = 7
∂g/∂x = 4x
∂g/∂y = 18y
Setting these equal to λ and solving for x and y, we get:
x = ±1/√2 and y = ±1/3√2
Now, we need to evaluate f(2,y) at these four points:
f(2,1/3√2) = 7(1/3√2) = (7/3)√2
f(2,-1/3√2) = 7(-1/3√2) = (-7/3)√2
f(2,1/√2) = 7(1/√2) = (7/√2)
f(2,-1/√2) = 7(-1/√2) = (-7/√2)
Therefore, the maximum value of f(2,y) on the ellipse is (7/√2) and the minimum value is (-7/3)√2.
To know more about partial derivatives, visit the link : https://brainly.com/question/30217886
#SPJ11
The Department of Health plans to test the lead level in a public park. The park will be closed if the average lead level exceeds the allowed limit of 400 parts/million, otherwise, the park will be kept open. The department conducts the test using soil samples gathered at randomly selected locations in the park. You work for the Department of Health and your concern is for public safety and overall health of communities In this situation, would you make alpha or beta as low as possible and why? Beta. This type of error would be that when the test was conducted, it indicated that the lead levels exceeded 400 parts/million, but it really didn't and the park was determined to be unsafe when it really wasn't. Alpha. This type of error would be that when the test was conducted, it indicated that the lead levels exceeded 400 parts/million, but it really didn't and the park was determined to be unsafe when it really wasn't. Alpha. This type of error would be that when the test was conducted, it indicated that the lead levels didn't exceed 400 parts/million, but it really did and the park was left open when it really wasn't. Beta. This type of error would be that when the test was conducted, it indicated that the lead levels didn't exceed 400 parts/million, but it really did and the park was left open when it really wasn't safe.
Answers
The correct answer is Beta. In this case, it is more important to make the Beta error as low as possible.
This is due to the Beta error being a false negative, which would suggest that the lead levels did not go above the permitted limit even though they did.
As a result, the park would continue to be open and the general public would be exposed to a potentially dangerous situation.
On the other side, a false positive (also known as an Alpha error) would cause the park to be closed without a need and would prevent the public from accessing a secure park.
Making the Beta error as small as feasible is therefore more crucial in order to protect the public from unwarranted dangers.
To learn more about Alpha visit:
https://brainly.com/question/14588341
#SPJ4
36 + 1.80 + 2.16 I'm stuck
Answers
Answer:
39.96 should be the right answer
Answer: 39.96
Step-by-step explanation:
36+1.80=37.80
Then you add 2.16
37.80+2.16=39.96
The two conditional relative frequency tables below show the results of a survey asking students whether they are taking a foreign language or not. A 4-column table with 3 rows. The first column has no label with entries middle school, high school, total. The second column is labeled taking a foreign language with entries 0.34, 0.66, 1.0. The third column is labeled not taking a foreign language with entries 0.64, 0.36, 1.0. The fourth column is labeled total with entries 0.4, 0.6, 1.0. Table B: Frequency of Foreign-Language Studies by Row A 4-column table with 3 rows. The first column has no label with entries middle school, high school, total. The second column is labeled taking a foreign language with entries 0.68, 0.88, 0.8. The third column is labeled not taking a foreign language with entries 0.32, 0.12, 0.2. The fourth column is labeled total with entries 1.0, 1.0, 1.0. Which table could be used to answer the question "Assuming a student is taking a foreign language, what is the probability the student is also in high school?”
Answers
Answer:
it's B
Step-by-step explanation:
Just took the test
Answer:
Its b
Step-by-step explanation:
For a pancake distribution of sin(a), where a = 0, determine the ratio of the average flux for e > 45 to the omnidirectional flux. What I need from here is:Directional Flux, Omnidirectional Flux,Directional Solid Angle, Omnidirectional Solid Angle. Then: Find the Flux per Solid Angle (For both the directional and omnidirectional cases) And find the ratio of those two
Answers
For the ratio of the average flux for e > 45 degrees to the omnidirectional flux, we divide the flux per solid angle for the directional case by the flux per solid angle for the omnidirectional case.
To find the ratio of the average flux for e > 45 degrees to the omnidirectional flux in a pancake distribution of sin(a) where a = 0, we need to calculate the directional flux, omnidirectional flux, directional solid angle, and omnidirectional solid angle.
Directional Flux:
The directional flux is the flux within a specific direction or range of angles. In this case, we are interested in e > 45 degrees.
Omnidirectional Flux:
The omnidirectional flux is the total flux in all directions or over the entire solid angle.
Directional Solid Angle:
The directional solid angle is the solid angle subtended by the specified direction or range of angles. In this case, it would be the solid angle corresponding to e > 45 degrees.
Omnidirectional Solid Angle:
The omnidirectional solid angle is the total solid angle subtended by all possible directions or over the entire sphere.
To find the flux per solid angle for both the directional and omnidirectional cases, we can use the formula:
Flux per Solid Angle = Total Flux / Solid Angle
Finally, to find the ratio of the average flux for e > 45 degrees to the omnidirectional flux, we divide the flux per solid angle for the directional case by the flux per solid angle for the omnidirectional case.
Learn more about Directional Flux at
brainly.com/question/28499883
#SPJ4
Figure A and B are similar. Figure A has a perimeter of 72 meters and one of the side lengths is 18 meters. Figure B has a perimeter of 120 meters Find The missing corresponding side length.
Answers
The missing corresponding side length in Figure B is 30 meters.
Perimeter is the total length of the boundary of a two-dimensional shape. It is found by adding up the lengths of all the sides of the shape.
How can we determine the missing corresponding side length ?Since Figure A and Figure B are similar, their corresponding side lengths are proportional.
Let's represent the missing side length in Figure B with x. Then, we can set up a proportion to solve for x:
18 / (72 - 3 × 18) = x / (120 - 3 × x)
Here, 72 - 3 × 18 represents the sum of the other three sides in Figure A, and 120 - 3 × x represents the sum of the other three sides in Figure B.
Simplifying the left-hand side, we get:
18 / (72 - 3 × 18) = 18 / 18 = 1
Substituting this into the proportion, we get:
1 = x / (120 - 3 × x)
Multiplying both sides by (120 - 3 × x), we get:
120 - 3 × x = x
Simplifying and solving for x, we get:
4x = 120
x = 30
Therefore, the missing corresponding side length in Figure B is 30 meters.
To know more about perimeter
brainly.com/question/6465134
#SPJ1
Are -1/3(-3m+6-12+15m) and 2(1-2m) equivalent
Answers
Algebraic expressions -1/3(-3m+6-12+15m) and 2(1-2m) are equivalent as they give same expression of simplifying.
What are equivalent algebraic expressions?
Equivalent expressions are expressions that work the same even though they look different. If two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value for the variable.
According the given question:
The given algebraic expressions in variable m are -1/3(-3m + 6- 12 + 15m) and 2(1 - 2m)
Simplifying 1st expression
-1/3(-3m + 6- 12 + 15m)
-1/3(-3m) -1/3(6) -1/3(-12) -1/3(15m)
m - 2 + 4 - 5m
-4m + 2 is the simplified form
Similarly simplifying 2nd expression
2(1 - 2m)
2 - 4m
Clearly both the algebraic expressions are same when simplified.
To know more about equivalent expressions visit
https://brainly.com/question/28170201
#SPJ1
which of the following lines are parallel.
Lines a and b
lines a and c
Lines b and c

Answers
The lines which are parallel are none.
What is the slope?The slope is the ratio of the vertical changes to the horizontal changes between two points of the line.
m = ( y₂ - y₁ ) / ( x₂ - x₁ )
where (x₁, y₁) and (x₂, y₂) are the two points that you are trying to find the slope between.
Given;
Coordinates of three lines
a;(1,5) and (-2,-4)
b;(3,2) and (1,-4)
c;(6,1) and (-4,2)
Now, slopes of the lines
a= -4-5/-2-1
=10/3
b=-4-2/1-3
=-3
c=2-1/-4-6
=1/-10
Therefore, by slopes of the line none of them are parallel.
Learn more about slope here:
https://brainly.com/question/2503591
#SPJ1
Can someone please help me with this question, I will mark branliest if it’s correct

Answers
Write a statement that correctly describes the relationship between these two sequences: 6, 7, 8, 9, 10, and 18, 21, 24, 27, 30. (2 points)
Answers
18, 21, 24, 27, 30 can be gotten when 6, 7, 8, 9, 10 are multiplied three times.
What is Sequence?Sequence is an ordered list of numbers that often follow a specific pattern or rule. Sequence is a list of things that are in order.
How to determine this
6, 7, 8, 9, 10 are related to 18, 21, 24, 27, 30
6 * 3 = 18
7 * 3 = 21
8 * 3 = 24
9 * 3 = 27
10 * 3 = 30
All of them followed the same sequence of being multiplied by 3.
6, 7, 8, 9, 10 when multiplied thrice will give 18, 21, 24, 27, 30.
Read more about Sequence
https://brainly.com/question/15458247
#SPJ1
the maclaurin series for the function f(x) is given by the formula x [infinity] n=1 (−1)n 1 x n 3n2 (n 5). the value of f (5)(0) (the 5-th derivative of f evaluated at x = 0) is A)-4/25 B)4/25 C)-1/750 D)1/750
Answers
The value of f(5)(0) for the given Maclaurin series is -1/750.
The Maclaurin series for a function f(x) is given by the formula:
f(x) = Σn=0 to infinity [f^(n)(0) / n!] x^n
where f^(n)(0) is the nth derivative of f evaluated at x=0.
In this case, we are given the Maclaurin series for the function f(x) as:
f(x) = x * Σn=1 to infinity (-1)^n (1 / (x^n * 3n^2 * (n+5)))
To find the 5th derivative of f(x) evaluated at x=0, we need to differentiate the series 5 times and then evaluate it at x=0.
f(1)(x) = Σn=1 to infinity (-1)^n (1 / (x^(n-1) * 3n^2 * (n+5)))
f(2)(x) = Σn=1 to infinity (-1)^n * (n-1) / (x^n * 3n^2 * (n+5))
f(3)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) / (x^(n+1) * 3n^2 * (n+5))
f(4)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) / (x^(n+2) * 3n^2 * (n+5))
f(5)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (x^(n+3) * 3n^2 * (n+5))
Substituting x=0, we get:
f(5)(0) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (0^(n+3) * 3n^2 * (n+5))
Simplifying the denominator, we get:
f(5)(0) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (3n^2 * (n+5))
To evaluate this series, we can use partial fraction decomposition and then use the formula for the sum of the series 1/n^2.
After simplifying, we get:
f(5)(0) = -1/750
Therefore, the value of f(5)(0) is -1/750, which is option (C).
Learn more about Maclaurin series here
https://brainly.com/question/28170689
#SPJ11
Find WX please help is very much appreciated

Answers
Answer:
WX = 6
Step-by-step explanation:
1. Approach
First, one must find the value of the variable (x). This can be done by using the Tangent-Line-intersection-theorem (many people refer to it by another name, but the theory is the same). This theory essentially states that when two lines are tangent to a circle and are non-parallel, the distance between the point of tangency, and the point of intersection of those two lines are the same for each line. After finding the value of (x), one can substitute it back into the given equation for the value of (WX), and solve it.
2. Finding (x)
The two segments; (WX) and (XY) are tangent to the given circle. Meaning that they only make contact with the circle at a single point. The space between their point of tangency and the point at which they intersect will be equal. Essentially meaning that the length of (WX) and the length of (XY) are the same. Therefore the equation
(XY) = (XW)
Can be formed. Substitute in the given values;
7x - 29 = 2x + 16
Inverse operations,
7x - 29 = 2x + 16
-2x -2x
5x - 29 = 16
+29 +29
5x = 45
/5 /5
x = 9
3. Solve for (WX)
Now substitute back in to find the length of (WX)
7x = 29
x = 5
7(5) - 29
35 - 29
6
Which dot plot corresponds to the values in the table?



Answers
A dot plot that corresponds to the values in the table include the following: dot plot B.
What is a dot plot?In Mathematics, a dot plot can be defined as a type of line plot that is typically used for the graphical representation of a data set above a number line, especially through the use of dots.
Based on the values contained in the table, the high school students' essays score on a scale of 0 to 10 should be plotted on a dot plot as follows:
An essay score of 3 would have 1 dot.
An essay score of 4 would have 1 dot.
An essay score of 5 would have 2 dots.
An essay score of 6 would have 5 dots.
An essay score of 7 would have 4 dots.
An essay score of 8 would have 7 dots.
An essay score of 9 would have 3 dots.
An essay score of 10 would have 2 dots.
Read more on dot plots here: brainly.com/question/18466974
#SPJ1
