A kite is stuck in a tree and Joe is holding the string. The angle formed
between the kite string and the tree is 50°. The distance between Joe
and the tree is 12 feet. How long is the kite string? Round to the nearest
tenth.
Answers
Answer:
15 feet
Step-by-step explanation:
Answer:
u04- (Saresp–2008) Nas Lojas Compre Aqui, um micro-ondas pode ser vendido de duas formas: à vista por R$ 299,00 ou em 12 parcelas iguais de R$ 32,15. As amigas Giovana e Mariana compraram, cada uma, um micro-ondas nessa loja: a primeira, à vista e a segunda, a prazo. Assinale a alternativa que mostra a quantia que Mariana pagou a mais do que Giovana.
2 pontos
a) R$ 22,50.
b) R$ 86,80.
c) R$ 129,30.
d) R$ 266,85.
e) Não houve diferença
Related Questions
Put the following equation of a line into slope-intercept form, simplifying all
fractions.
4x + 5y = 20
Answers
Answer:
y=4-(4/5)x or y= -4/5x+4
Step-by-step explanation:
4x+5y=20
5y=20-4x
y=(20-4x)/5
y=(20/5)-(4x/5)
y=4-(4/5)x or y= -4/5x+4
please help me out...

Answers
Answer: B its associative property
Step-by-step explanation:
i have a feeling its B im sorry if im wrong
What is the volume of a cone with a diameter of 30 feet and a height of 600 feet? Use 3.14 for tt

Answers
Answer:
the volume is about 1884
Step-by-step explanation:
v of cone= 1/3(pi)r^2h
diameter to radius is 30=5.477225575051661
so 1/3(3.14)5.477225575051661^2(60)
=1/3(3.14)30(60)
=1/3(5652)
=1884
hope this helps
I really need help with this question !!!!!!!!!!!!!!!!!

Answers
Solve each equation using the Quadratic Formula.
25x²-30 x+9=0
Answers
In this case, the coefficient of x² is 25, the coefficient of x is -30, and the constant term is 9. The solution to the equation 25x²-30x+9=0 using the Quadratic Formula is x = 3/5.
To solve the equation
25x²-30x+9=0
using the Quadratic Formula, we can first identify the coefficients of the quadratic equation.
In this case, the coefficient of x² is 25,
the coefficient of x is -30, and the constant term is 9.
The Quadratic Formula is given by
x = (-b ± √(b² - 4ac)) / (2a),
where a, b, and c are the coefficients of the quadratic equation.
By substituting the values into the formula, we have:
x = (-(-30) ± √((-30)² - 4(25)(9))) / (2(25))
x = (30 ± √(900 - 900)) / 50
x = (30 ± √0) / 50
Since the discriminant (√(b² - 4ac)) is equal to zero, we have a single real root.
Simplifying further:
x = (30 ± 0) / 50
x = 30 / 50
x = 3 / 5
Therefore, the solution to the equation 25x²-30x+9=0 using the Quadratic Formula is x = 3/5.
To know more about Quadratic Formula visit:
https://brainly.com/question/22364785
#SPJ11
If the slopes are
there will be one solution.
A)the same
B)different
Answers
Answer:
the same
Step-by-step explanation:
if there is only one solution then both slopes must be the same
What value of z should we use when making a 93% confidence interval for p? A. 1.48 B. It's impossible to make a 93% CI. C. 2.70 D. 1.81
Answers
The value of z that should be used when making a 93% confidence interval for p is Z=1.81 that is option D.
The z score is a measure of how many standard deviations a raw score is below or above the population mean. It will be positive if the value is more than the mean and negative if it is less than the mean. It is often referred to as the standard score. It represents the number of standard deviations an entity has from the mean.
To utilise a z-score, both the mean and the population standard deviation must be known. The z score calculates the likelihood of a score occuring within a standard normal distribution. It also allows us to compare scores from various samples. A table for the values of, representing the values of the cumulative distribution function of the normal distribution, is known as a
At 93% confidence, the significance level is,
ɑ= 1-0.93
ɑ= 0.07
Divide alpha by 2,
ɑ/2= 0.07/2= 0.035
Now, from the ‘normal probability’ table, the z value corresponding to the inverse probability of 0.035 is 1.81.
As a result, the z value is 1.81 at 93% confidence level.
z= 1.81
The value for z score is 1.81
Learn more about Confidence interval :
https://brainly.com/question/27325376
#SPJ4
Find the value of this expression and show ur work

Answers
Answer:
-30/49
Step-by-step explanation:
You multiply the numbers, then add the negative symbol, when you multiply the numbers, you get:
10/7*3/7 which equals 30/49, which means the answer is -30/49
(How many terms are needed in the series for cosx to compute the value of cosx for |x | ≤ 1/1/12 accurate to 12 decimal places (rounded)? Name the theorem you are using to get to the solution. (4+1)
Answers
The value of cos(x) for |x| ≤ 1/12 accurate to 12 decimal places (rounded), we need at least 5 terms in the series of cos(x). We will use Taylor's theorem to derive this result.
Taylor's theorem, also known as the Taylor series theorem, is a mathematical formula used to represent functions as a sum of infinitely many derivatives in order to approximate them over a certain interval.
This formula allows us to derive the value of a function at a point using information about its derivatives at that point.
In essence, Taylor's theorem is a tool used in calculus to model complex functions that cannot be easily solved.
Using Taylor's theorem to solve the question:
We know that the Taylor series expansion of cos(x) is given by the formula:
cos(x) = 1 - x²/2! + x⁴/4! - x⁶/6! + ...
To get an accurate value of cos(x), we need to keep adding terms in the series until the absolute value of the next term is less than our required accuracy.
Using |x| ≤ 1/12 and rounding to 12 decimal places, we have an error tolerance of 0.000000000001.
Therefore, we need to find the smallest value of n such that \(|x^(n+1)/(n+1)!| ≤ 0.000000000001,\)
where x = 1/12.
Substituting x = 1/12,
we have |(1/12)^(n+1)/(n+1)!| ≤ 0.000000000001
Using a calculator, we can find that n = 4 satisfies this inequality.
Therefore, we need at least 5 terms in the series of cos(x) to compute the value of cos(x) for |x| ≤ 1/12 accurate to 12 decimal places (rounded).
Conclusion:
To calculate the value of cos(x) for |x| ≤ 1/12 accurate to 12 decimal places (rounded), we need at least 5 terms in the series of cos(x). We used Taylor's theorem to derive this result.
To know more about Taylor's theorem visit
https://brainly.com/question/13264870
#SPJ11
a book seller sold a book for $100 and thereby gains $20. Find his gain per cent a) 20% b) 25% c)40% d) none of the above. plz i need help asap
Answers
Answer:
a.20%
Step-by-step explanation:
because of the book is 100$ and the thereby sold it and gained 20$ equals to 20%
the coefficient of determination measures the variation in the dependent variable that is explained by the regression model.T/F
Answers
The statement "the coefficient of determination measures the variation in the dependent variable that is explained by the regression model" is true because coefficient of determination, or R-squared, measures the proportion of variance in the dependent variable that is explained by the independent variables in a regression model.
The coefficient of determination, or R-squared, is a statistical measure that evaluates the goodness of fit of a regression model. It quantifies the amount of variance in the dependent variable that can be explained by the independent variables in the model. R-squared ranges from 0 to 1, where a value of 0 means that none of the variation in the dependent variable is explained by the model, while a value of 1 indicates that all the variation is explained.
Therefore, R-squared is useful in assessing the predictive power of a model, and higher values are generally preferred. However, it is important to note that R-squared alone does not guarantee a good model, and other factors such as model assumptions and outliers should also be considered.
Learn more about coefficient of determination here
brainly.com/question/14115325
#SPJ4
2n+1=157 what is the first number
Answers
a survey of college students reported that they spend an average of $9.50 a day on dinner with a standard deviation of $3. what is the probability that 100 randomly selected college students will spend less than $10.00 on average for dinner? round your answer to 4 decimal places.
Answers
The probability that 100 randomly selected college students will spend less than $10.00 on average for dinner is approximately 0.9525 or 95.25%.
We can utilize as far as possible hypothesis to inexact the conveyance of test implies for an enormous example size of 100. The example mean is regularly dispersed with a mean of the populace mean ($9.50) and a standard deviation of the populace standard deviation partitioned by the square base of the example size ($3/sqrt(100) = 0.3).
To find the likelihood that 100 arbitrarily chosen understudies will spend under $10.00 on normal for supper, we really want to find the z-score related with the worth $10.00 utilizing the recipe:
z = (x - mu)/(sigma/sqrt(n))
Subbing the given qualities, we get:
z = (10 - 9.5)/(0.3) = 1.67
Utilizing a standard typical dissemination table or number cruncher, we can find that the likelihood of a z-score under 1.67 is roughly 0.9525.
Accordingly, the likelihood that 100 haphazardly chosen understudies will spend under $10.00 on normal for supper is roughly 0.9525 or 95.25%.
To learn more about probability, refer:
https://brainly.com/question/3662142
#SPJ4
scores on a university math placement exam are normally distributed with a mean of 42 and a standard deviation of 19. students who score in the top 20% will be eligible to enroll in calculus. what is the minimum score required to be eligible? round your answer to the nearest integer.
Answers
So the minimum score required to be eligible to enroll in calculus is 67.
To find the minimum score required to be in the top 20%, we need to find the score that corresponds to the 80th percentile of the distribution.
The standard normal distribution is a normal distribution with mean 0 and standard deviation 1. We can use the standard normal distribution to find percentiles of any normal distribution by using the fact that any normal distribution can be converted to a standard normal distribution through the following formula:
z = (x - mean) / standard deviation
where x is the raw score, mean is the mean of the distribution, standard deviation is the standard deviation of the distribution, and z is the standardized score (also called the z-score).
We can use this formula to convert the scores on the math placement exam to the standard normal distribution. Let x be the minimum score required to be eligible. Then the corresponding z-score would be:
z = (x - 42) / 19
We want to find the value of x that corresponds to the z-score for the 80th percentile, which we can find using a z-table or by using a calculator or computer to find the inverse of the standard normal cumulative distribution function (CDF). The z-score for the 80th percentile is approximately 0.84. Plugging this value into the equation above, we get:
0.84 = (x - 42) / 19
Solving for x, we find that the minimum score required to be eligible is approximately 66. Rounding to the nearest integer, the minimum score required is 67.
So the minimum score required to be eligible to enroll in calculus is 67.
To learn more about standard normal distribution,
visit; brainly.com/question/13781953
#SPJ4
What is the surface area ?

Answers
Answer:
C 90 ft³
Step-by-step explanation:
surface area = 2 (h · l + h · w + l · w)
The measurements of this rectangular prism is:
h = 2
w = 5
l = 5
2 (2 · 5 + 2 · 5 + 5 · 5)
Using PEMDAS, we have:
2 (10 + 10 + 25)
2 (45)
90 ft cubed
5. Use the information to answer the following question.The quadratic function f is represented by the equallon f(x) = x2 - +5.The table gives some of the values of the exponential function g.X- 1o123g(x)124816Which of the following statements is TRUEa. The y-Intercept of g(x) is greater than the y-intercept of f(x).b. The functions f(x) and g(x) have the same value at x = 1.c. Both functions have a domain of all real numbers.d. f(3) > g(3)

Answers
Substitute 0 for x in the equation to determine the y-intercept.
\(\begin{gathered} f(0)=(0)^2-0+5 \\ =5 \end{gathered}\)So y-intercept of function f(x) is more than y-intercept of g(x).
Substitute 1 for x in the equation to obtain the value of function at x = 1.
\(\begin{gathered} f(1)=(1)^2-1+5 \\ =5 \end{gathered}\)The function f(x) and g(x) have different vlue at x = 1.
Substitute 3 for x in the function to obtain f(3).
\(\begin{gathered} f(3)=(3)^2-3+5 \\ =9-3+5 \\ =11 \end{gathered}\)So g(x) > f(x)
The quadratic function is defined for all values of x and exponential function is also defined for all values of x. So domain of both function f(x) and g(x) is all real numbers.
So correct option is option C.
Write number sentences using multiplication to show: A. The fraction represented in 1(a) is equivalent to the fraction represented in 1(b).

Answers
Answer: We have to write two fractions that are equivalent to 1(a) and 1(b):
1(a) Equivalent fraction to 1(b):
\(\begin{gathered} (a)\Rightarrow\frac{1}{3}=\frac{1}{3}\times\frac{2}{2}=\frac{2}{6} \\ \text{ Equivalent fraction is:} \\ \frac{2}{6}\Rightarrow1(b) \end{gathered}\)Conclusion: The two fractions are Indeed the Equivalent!
How many numbers less than 305 are divisible by 3?
Answers
To find the number of integers less than 305 that are divisible by 3, we can divide 305 by 3 and round down to the nearest integer. This gives us 101. However, we need to subtract 1 to exclude the number 305 itself, so there are 100 numbers less than 305 that are divisible by 3.
In math, what exactly is a divisible?A number is said to be divisible if it divides evenly (leaving no residue). 34, for instance, is divisible by 2 since 2 enters 34 equally. 34 is not divisible by 3 since it would result in a remainder.
How can you divide three?According to the three-digit rule of division, a whole number is said to be divisible by three if the total of all its digits is precisely divided by three. A number's ability to be divided by three can be determined without executing division.
To know more about divisible visit:
https://brainly.com/question/21416852
#SPJ4
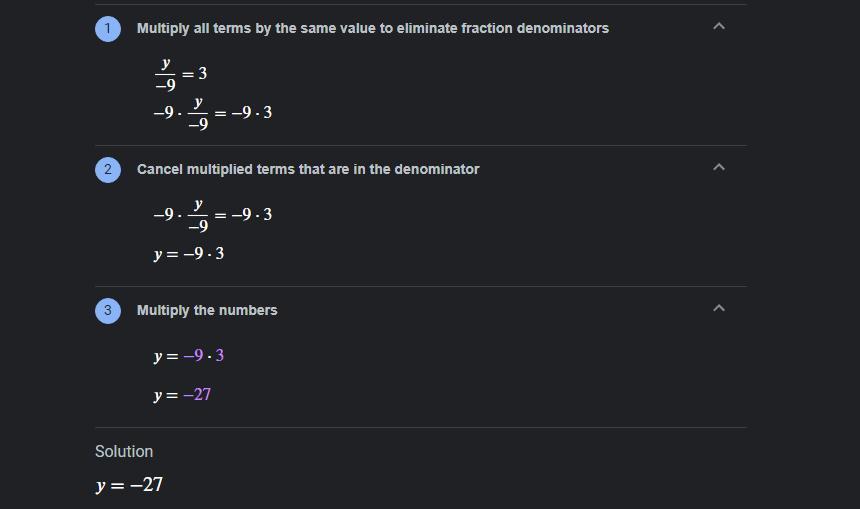
Y÷-9=3 solution please with every single steps
Answers
Answer:
Your solution is y = -27
Step-by-step explanation:
The image below shows the steps. (Mark brainliest if this helps please! ) :)
I need a step-by-step process on how to do:
-3x+y=9
y=x-7
I would think this is a substitution problem.
Answers
Answer:
x = -8
y = -15
Step-by-step explanation:
-3x + y = 9
y = x - 7
-3x + x - 7 = 9
-2x - 7 = 9
-2x = 16
2x = -16
x = -8
y = -8 - 7
y = -15
Pleeaase help.......
Select ALL the correct answers
Which equations have infinitely many solutions?

Answers
Answer:
The 1st, 3rd and 4th
Step-by-step explanation:
Answer:
Options B and D
Step-by-step explanation:
Let's solve each equation:
x-3x=-2x+4
-2x=-2x+4
0=4
No solutions, so A is wrong
x-1/3(3x)=0
x-(3x/3)=0
x-x=0
0=0
Infinitely many solutions, so B is correct
1/3x-3=4+2x
1/3x=7+2x
-5/3x=7
x=-21/5
One solution, so C is incorrect
3x+2-1/3(3x)=2+2x
3x+2-(3x/3)=2+2x
3x+2-x=2+2x
2x+2=2+2x
2x=2x
0=0
Infinitely many solutions, so D is correct
x-1/3x+2=0
2/3x+2=0
2/3x=-2
x=3
One solution, so E is incorrect
As you can see, when both sides of the equations are equal to each other such as 0=0 and x=x, you'll always have infinitely many solutions. Therefore, options B and D are correct
If (x + a) is a factor of a polynomial function, (p) &, which two statements are true? - The binomial (x – a) is also a factor of p(x). - The value of p(a) must be 0. - The value of p(-a) must be 0. - There is an 2-intercept of the function at (-a,0). - There is an z-intercept of the function at (a,0).
Answers
Answer:
The value of p(-a) must be 0
There is an x intercept of the function at (-a,0)
Step-by-step explanation:
(x + a) is a factor of a function p(x)
that means, that p(x) must have an x-intercept at the point x = -a
This can be written in two different ways,
p(-a) = 0x-intercept of the function p(x) at (-a,0)If (x + a) is a factor of a polynomial function, p(x), then the two statements that are true are:
The value of p(a) must be 0.There is an z-intercept of the function at (a,0).A factor of a polynomial function is a binomial that, when multiplied by another polynomial, gives the original polynomial function. If (x + a) is a factor of p(x), then p(x) can be written as (x + a)q(x), where q(x) is another polynomial function.
According to the Factor Theorem, if (x + a) is a factor of p(x), then p(a) = 0. This means that the value of the polynomial function at x = a is 0.
Additionally, if p(a) = 0, then there is an z-intercept of the function at (a,0). This is because the z-intercept is the point where the function crosses the z-axis, and this occurs when the value of the function is 0.
Therefore, the two statements that are true are "The value of p(a) must be 0" and "There is an z-intercept of the function at (a,0)".
Learn more about Polynomial Function here: brainly.com/question/12976257
#SPJ11
please fill in the final row (x)

Answers
Answer:
x = 11
Step-by-step explanation:
The Frequency column has to total 50 ( number of rolls on dice )
Thus total the given frequencies and equate to 50, that is
12 + 8 + 7 + 3 + 9 + x = 50
39 + x = 50 ( subtract 39 from both sides )
x = 11
Answer:
x=11
Step-by-step explanation:
12+8+7+3+9=39
50-39= 11
Help I need a answer

Answers
Answer:
C
Step-by-step explanation:
The verticle line on the left is the minimum and is 4 for both
Which relation is also a function?
{ (1,0), (2,2), (1,3) }
{ (1, 2), (1, 4), (2, 6) }
{ (2, 1), (2, 2), (2, 3) }
{ (0, 0), (4, 0), (6, 0) }
Answers
Answer:
{ (0, 0), (4, 0), (6, 0) }
Step-by-step explanation:
In order to be a function, ordered pairs must have values of x, or the domain, that are different and do not repeat.
A system of equations is created by using the line represented by 2x+4y=0 and the line represented by the data in
the table below.
3
5
6
y
8
-4
-10
-13
What is the x-value of the solution to the system?
Answers
The solution of the system of equations is:
(4.72, -2.32)
How to solve the system of equations?One of the lines of the system is represented by the table:
x y
3 8
5 -4
6 -10
Remember that a general linear equation is:
y = a*x + b
Where a is the slope and b the y-intercept.
Using that table, from 5 to 6 we can see that the value of y decreaes by 6 units, then the slope is:
y = -6x + b
To find the value of b, we can replace the first point (3, 8), then we will get:
8 = -6*3 + b
8 = -18 + b
8 + 18 = b
26 = b
Then the system of equations is:
2x + 4y = 0
y = -6x + 26
Replacing the first equtaion into the second one we get:
2x + 4*( -6x + 26) = 0
2x - 24x + 104 = 0
-22x = -104
x = -104/-22 = 4.72
And the value of y is:
y = -6*4.72 + 26 = -2.32
Learn more about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
Rewrite the function by completing the square. X^2-6x-16=0
Answers
The function \(x^2 - 6x - 16 = 0\) can be rewritten by completing the square as \((x - 3)^2 = 9\), and the solution is x = 6.
The equation given is in the form of ax^2 + bx + c = 0, where a = 1, b = -6, and c = -16. To complete the square, we must first divide the coefficient of x (which is b/2) from both sides of the equation, and then take the square root of both sides.
We will then add (b/2)^2 to both sides of the equation to get the equation in the form of
(x+b/2)^2 = c + (b/2)^2.
We can then simplify the equation to get (x+b/2)^2 = c + (b/2)^2,
which can be rewritten as
(x+b/2)^2 = (b^2/4) - 16.
Therefore, the equation can be rewritten as (x+b/2)^2 = (b^2/4) - 16,
which simplifies to (x - 3)^2 = 9.
To solve for x, we can take the square root of both sides and add 3 to the right side, yielding x = 6.
To learn more about Function :
https://brainly.com/question/11624077
#SPJ11
Which of the following functions is graphed below?

Answers
Answer:b I’m pretty sure
Step-by-step explanation:
Audrey is planning to drive from City X to City Y. The scale drawing below shows the distance between the two cities with a scale of ¼ inch = 24 miles.
City X
City Y
3 in
Answers
The actual distance between the two cities is 288 miles.
What is the actual distance?A scale drawing is a smaller version of a larger image / city. The scale drawing is reduced by a constant ratio. This means that the scale drawing of the two cities would be smaller than the actual cities.
The scale is used to keep the proportion of the dimensions between the scale drawing and the original diagram similar. This means that the scale drawing of the two cities would be smaller than the actual cities.
The actual distance between the two cities = (3 x 24) ÷ 1/4
= 3 x 24 x 4 = 288 miles
To learn more about scale drawings, please check: https://brainly.com/question/26388230
#SPJ1

What’s the Y-intercept of the parabola with the equation y= x^2 - 4x-10?
Answers
Answer:
-10
Step-by-step explanation:
Plug in 0 to the equation ('cause y-intercept is found when "x" =0), and u get -10.
The constant is typically the y-intercept.