A local business has sold 5000 tickets to a raffle. Each ticket is numbered. The business randomly samples 10 tickets to win the same prize. They select the sample of winners using a random number generator to select 10 numbers from 1 to 5000. The sample of 10 prize winners is an example of what type of sampling scheme
Answers
The sample of 10 prize winners from the 5000 tickets in the raffle is an example of simple random sampling without replacement.
Simple random sampling involves randomly selecting individuals from a population in such a way that each individual has an equal chance of being chosen. In this case, the 5000 tickets represent the population, and the business uses a random number generator to select 10 tickets as the prize winners.
The "without replacement" aspect means that once a ticket is selected as a winner, it is removed from the pool of available tickets for subsequent selections. This ensures that each ticket can only win the prize once, maintaining the randomness and fairness of the selection process.
Simple random sampling without replacement is a common sampling scheme used in various contexts, including raffles, surveys, and statisticalresearch. It provides a representative subset of the population, allowing for generalizations and conclusions to be drawn about the larger population based on the characteristics of the sample.
Learn more about statistical here:
https://brainly.com/question/31538429
#SPJ11
Related Questions
Find an equation doe the line that is tangent to the curve y=3x^3-3x at the point (-1,0)
Answers
The tangent to the given curve at the point (1,0) is: y=6x-6.
What is tangent?The straight line that "just touches" the curve at a given location is referred to as the tangent line to a plane curve in geometry. It was described by Leibniz as the path connecting two points on a curve that are infinitely near together.When you ride a bicycle, every point on the wheel's circumference forms a tangent with the road, providing a practical illustration of a tangent.When you ride a bicycle, every point on the wheel's circumference forms a tangent with the road, providing a practical illustration of a tangent.A straight line that only touches a circle once is said to be tangent to it. The term "point of tangency" refers to this location.The first derivative f'(x), the slope (tangent) of the original curve, may be obtained at every point (x,y) on the curve because the supplied curve is a continuous function, making Eq. 1 differetiable at every x.
The slope of the tangent at x=1 is given by the first derivative of Eq. 1: f'(1)=9(1)2-3=6.
A line that passes through the point (x1, y1) and has a slope of m has the equation:
(y-y1)=m(x-x1) ··· Eq.2 (the point- slope form of linear function)
Here, x1=1, y1=0, and m=f'(x1)=6. Add these numbers to Eq. 2. It is possible to repeat and simplify Eq. 2 as follows: y-0=6(x-1) ⇒ y=6x-6
Consequently, y=6x-6 is the tangent to the given curve at position (1, 0).
To learn more about the tangent, refer to:
https://brainly.com/question/14790856
#SPJ4
Layla's Cupcakes recently sold 7 coconut cupcakes and 14 other cupcakes. Considering this data, how many of the next 9 cupcakes sold would you expect to be coconut cupcakes?
Answers
Answer:
3 of 9 is expected
since 7 of 21 (7+14) is 1/3 are coconut cupcake
7/21 = 1/3
1/3 x 9 = 3 coconut cupcakes
Triangle J L N is cut by line segment K M. LIne segment K M goes from side J L to side L N. The length of J K is 10, the length of K L is 16, the length of L M is 24, and the length of M N is 15. Is KM ∥ JN? Why or why not? No, because StartFraction 16 Over 10 EndFraction not-equals StartFraction 24 Over 15 EndFraction. Yes, because StartFraction 10 Over 24 EndFraction equals StartFraction 15 Over 16 EndFraction. Yes, because StartFraction 16 Over 10 EndFraction equals StartFraction 15 Over 24 EndFraction Yes, because StartFraction 16 Over 10 EndFraction equals StartFraction 24 Over 15 EndFraction.
Answers
Answer:
D. Yes, because StartFraction 16 Over 10 EndFraction equals StartFraction 24 Over 15 EndFraction.
Step-by-step explanation:
When two line are parallel, they do not meet even with continuous extension of their length.
In the given triangle JLN, line segment KM would be parallel to side JN if;
\(\frac{KL}{JK}\) = \(\frac{LM}{MN}\)
Given that: KL = 16, JK = 10, LM = 24 and MN = 15.
⇒ \(\frac{16}{10}\) = \(\frac{24}{15}\)
\(\frac{8}{5}\) = \(\frac{8}{5}\)
Therefore, since the ratios are the same then KM ∥ JN. So that the statement; Yes, because \(\frac{16}{10}\) equals \(\frac{24}{15}\) is correct.
Answer:
The answer is D on edge.
Just wanna help out, have a nice day!
The polling results show the ratio of votes for candidate A to candidate B
15 18
25 30
35 42
45 ?
at this rate, if candidate A received 45 votes did candidate B receive
ANSWERS: A.54 B.56 C.60 D.90
Answers
Answer:
54
Step-by-step explanation:
if you look at the ratios between the values of A and B. you will see that the successive values of A increase by 10 while B increase by 12
Therefore for A
35 + 10 = 45
for B
42 + 12 = 54
Any answers ??? I can’t do it

Answers
The missing value that completes the frequency table is 100
What is a Frequency Table?A frequency table is just a two-column "t-chart" or table that lists all of the potential outcomes and their corresponding frequencies as seen in a sample.
How to solve:
From the graph given,
The battery life(hours) from x = 15 to x= 20 has a frequency of 130
The battery life(hours) from x= 28 to x= 30 has a frequency of 100
It can be inferred that from the battery life of the different models, the missing value is 100 and when you crosscheck the data, you would find this is correct and accurate.
Read more about frequency table here:
https://brainly.com/question/27820465
#SPJ1
1.) Jeffjust bought a house on a triangular lot. The
sides measure 85 feet. 132 feet, and 157 feet. Is his
lot a right triangle?
Answers
Answer:176 feet
Step-by-step explanation:because you multiply all sides of the triangle
please solution
this question quickly
If the standard
time is 234.15 minute and the basic time is 233.4 minute, the
allowance time is:
0.75
minute
0.57
minute
0.80
minute
Answers
The allowance time, if the standard time is 234.15 minutes and the basic time is 233.4 minutes is 0.75 minute
To calculate the allowance time, we can use the following formula:
Allowance time = Standard time - Basic time
Thus, Allowance time = 234.15 minutes - 233.4 minute = 0.75 minutes
Therefore, the allowance time is 0.75 minutes.
Learn more about allowance time, here:
https://brainly.com/question/30011892
I NEED HELP ASAP ! THIS IS FOR A PAST DUE QUIZ. THEY ARE GIVING ME ONE MORE CHANCE
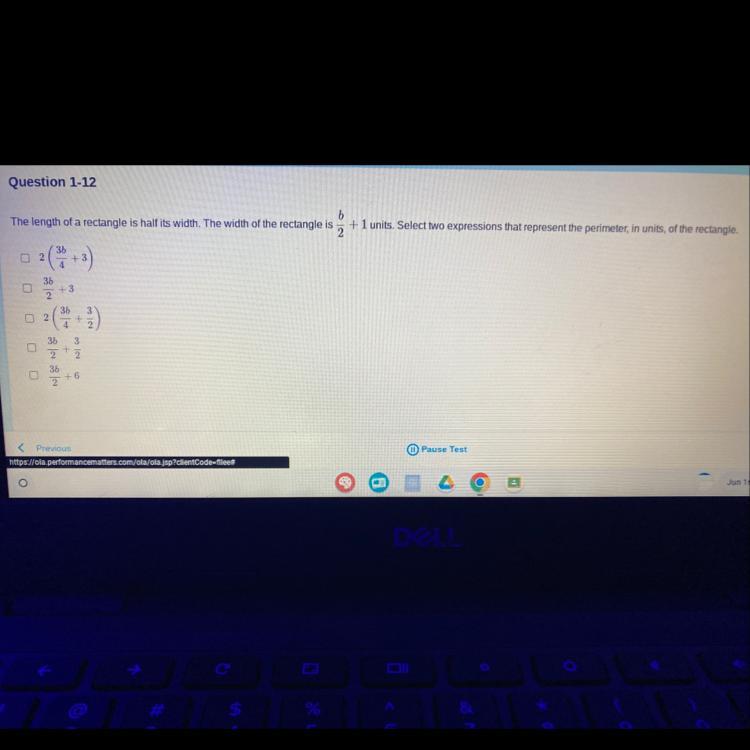
Answers
Answer:
3b/2 + 3
Step-by-step explanation:
The formula to calculate perimeter of rectangle is 2l + 2w
The length is half the width so length is 1/2 (b/2 +1), which when simplified is b/4 + 1/2
Using the formula to calculate perimeter you can substitute and calculate
p= 2l + 2w
p= 2(b/4 + 1/2) + 2(b/2 + 1)
p= 2b/4 +2/2 + 2b/2 +2
p= 1/2b + 1 + b + 2
p= 3/2b + 3
Simplified it's 3b/2 +3
A student must study for 20 to 30 hours a week to maintain their grade point average. If the
student wants to study daily, how many hours per day is this (in interval notation)?
0 (20,30)
[20/7,30/7]
[13,23]
[27,37]
Answers
That gives you an idea of how long each day the student must study in order to maintain their GPA
please help with this quesriom

Answers
Answer:
True
Step-by-step explanation:
Just a guess
A dog weighs `20\%` more than it did three months ago. It weighs `36` pounds now.
How much did the dog weigh three months ago?
Answers
The dog weigh 30 pounds three months ago.
What is Algebra?A branch of mathematics known as algebra deals with symbols and the mathematical operations performed on them.
Variables are the name given to these symbols because they lack set values. In order to determine the values, these symbols are also subjected to various addition, subtraction, multiplication, and division arithmetic operations.
Given:
Present weight of dog = 36 pounds
and, three months ago the dog weigh 20% more.
let the dog weight x pounds three months ago.
So, 20% more than x is 1.2x.
Then, 1.2x = 36
x = 36/1.2
x = 30 pounds
Hence, the dog weigh 30 pounds.
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ1
solve sinx = 2x-3 using false position method
Answers
The root of the equation sinx = 2x-3 is 0.8401 (approx).
Given equation is sinx = 2x-3
We need to solve this equation using false position method.
False position method is also known as the regula falsi method.
It is an iterative method used to solve nonlinear equations.
The method is based on the intermediate value theorem.
False position method is a modified version of the bisection method.
The following steps are followed to solve the given equation using the false position method:
1. We will take the end points of the interval a and b in such a way that f(a) and f(b) have opposite signs.
Here, f(x) = sinx - 2x + 3.
2. Calculate the value of c using the following formula: c = [(a*f(b)) - (b*f(a))] / (f(b) - f(a))
3. Evaluate the function at point c and find the sign of f(c).
4. If f(c) is positive, then the root lies between a and c. So, we replace b with c. If f(c) is negative, then the root lies between c and b. So, we replace a with c.
5. Repeat the steps 2 to 4 until we obtain the required accuracy.
Let's solve the given equation using the false position method.
We will take a = 0 and b = 1 because f(0) = 3 and f(1) = -0.1585 have opposite signs.
So, the root lies between 0 and 1.
The calculation is shown in the attached image below.
Therefore, the root of the equation sinx = 2x-3 is 0.8401 (approx).
Learn more about equation
brainly.com/question/29657983
#SPJ11
1 Problem 1 1.1 a Consider a collection {X₁,..., Xn} of random variables such that X;~ Unif(0, 1). Find the CDF and PDF of the X(), the maximum order statistic (Hint: Look up the Beta Distribution a
Answers
The density of X () is given by the formula: f (t) = n t^n-1 (1-t)^0 0 < t < 1.
X () is the maximum order statistic of a random sample of size n from the uniform distribution with parameters 0 and 1. The cumulative distribution function (CDF) of X () is given by the probability that the maximum value of the sample does not exceed the threshold t:
The PDF can be obtained by differentiation as:where the constant C is chosen such that the integral over the entire real line of f (t) is equal to one.
For that purpose, let U = X, V = X, and consider the joint density of (U, V) with integration limits 0 < u < 1 and u < v < 1, which is given by:
Now, integrate this joint density over the triangle 0 < u < v < 1.
By Fubini's theorem, the result is independent of the order of integration:
To get the value of C, notice that the inner integral is the CDF of a beta distribution with parameters (2, n-1), so C can be found as:
Thus, the density of X () is given by the formula: f (t) = n t^n-1 (1-t)^0 0 < t < 1.
Know more about density here,
https://brainly.com/question/29775886
#SPJ11
Hector is building a metal sculpture in the shape of an equilateral triangle. After he divides ametal bar into 3 equal pieces, Hector figures each side of the triangular sculpture can be atmost 9 feet long.Let x represent the perimeter of the triangular sculpture. Which inequality describes theproblem?
Answers
One of the properties of an equilateral triangle is that all the sides are equal
From the statement given, each of the lengths of the triangle is at most 9 feet long means that each of the lengths is less than or equal to 9 feet
This can be represented mathematically as
\(\begin{gathered} l\leq9ft \\ \text{Where l is the length} \end{gathered}\)The perimeter of an equilateral triangle is the addition of the three equal lengths i.e.
\(l+l+l=\text{ 3l}\)If x represents the perimeter, then
Let I and J be ideals and P a prime ideal of R. Prove that if I J ⊆ P then I ⊆ P or J ⊆ P.
Answers
We have shown that if IJ ⊆ P, then either I ⊆ P or J ⊆ P. Hence, the statement is proven, for I and J be ideals and P a prime ideal of R. Since P is prime, so we have the following inequality:(I intersection P) (J intersection P) ⊆ P²
Now, since P is prime so P² is a prime ideal too, thus one of the ideals I intersection P and J intersection P must be contained in P.
If I intersection P ⊆ P, then I ⊆ P. If J intersection P ⊆ P, then J ⊆ P. Therefore, I ⊆ P or J ⊆ P.
To prove the statement, let's assume that I and J are ideals of a ring R, and P is a prime ideal of R. We want to show that if IJ ⊆ P, then either I ⊆ P or J ⊆ P.
Suppose that IJ ⊆ P, We will proceed by contradiction.
Assume that I is not contained in P, which means there exists an element a ∈ I such that a ∉ P.
Since P is a prime ideal, it is closed under multiplication, so aJ ⊆ PJ ⊆ P.
Now consider the product (aJ)(a⁻¹). Since a ∉ P, a⁻¹ ∈ R\P (the complement of P in R).
Therefore, (aJ)(a⁻¹) ⊆ P(a⁻¹), and we have:
aJ ⊆ P(a⁻¹)
Multiplying both sides by a, we get:
a(aJ) ⊆ a(P(a⁻¹))
a²J ⊆ Pa⁻¹
Since J is an ideal, a²J ⊆ aJ ⊆ P(a⁻¹), and by induction,
we have aⁿJ ⊆ Pa⁻ⁿ for any positive integer n.
Consider the element aⁿ ∈ aⁿJ.
Since aⁿJ ⊆ Pa⁻ⁿ, aⁿ ∈ Pa⁻ⁿ.
This implies that aⁿ is an element of the prime ideal P for any positive integer n.
Since R is a ring, there exists a positive integer m such that aᵐ = aᵐ⁺¹ for some m⁺¹ > m.
This means that aᵐ (a - 1) = 0.
Since aᵐ ∈ P and P is a prime ideal, either a or (a - 1) must be in P.
If a is in P, then I ⊆ P, which is one of the conditions we want to prove.
If (a - 1) is in P, then consider the element 1 ∈ R. Since (a - 1) is in P, we have 1 - (a - 1) = a ∈ P.
This implies J ⊆ P, which is the other condition we want to prove.
In either case, we have shown that if IJ ⊆ P, then either I ⊆ P or J ⊆ P. Hence, the statement is proven.
To know more about intersection, visit:
https://brainly.com/question/29185601
#SPJ11
2x squared -2x-6 Factor out the GCF
Answers
Solution:
Given:
\(2x^2-2x-6\)The greatest common factor (GCF) of a set of numbers is the largest factor that all the numbers share.
The greatest common factor between the terms is 2.
Factoring out the GCF,
\(undefined\)Use the property of equality to solve this equation 4.5x=18
Answers
Answer:
x = 4
Step-by-step explanation:
Given
4.5x = 18 ( divide both sides by 4.5 )
x = 4
Answer:
x=4
Step-by-step explanation:
to isolate x, we need to divide both sides by 4.5, and 18/4.5 is equal to 4, so x=4.
1. What is the Least Common Multiple of 2 and 8?
Answers
Answer:
the least common multiple is 8
I need help with this problem. I don't understand what it means.

Answers
ANSWER:
\(-\frac{1}{3}\pi\)STEP-BY-STEP EXPLANATION:
Degrees and radians are two different systems for measuring angles. An angle of 360 ° equals 2π radians; an angle of 180 ° equals π radians.
Therefore the formula is the following:
\(x\cdot\frac{\pi}{180}=-60\cdot\frac{\pi}{180}=-\frac{1}{3}\pi\)Explain how to solve 2x + 1 = 9 using the change of base formula. Include the solution for x in your answer. Round your answer to the nearest thousandth.
a. x = log(9/2 + 1) / log(2)
b. x = log(9/2 - 1) / log(2)
c. x = log(9 + 1) / log(2)
d. x = log(9 - 1) / log(2)
Answers
Therefore, none of the options provided (a, b, c, d) accurately represents the solution to the equation. The correct solution is x = 4.
To solve the equation 2x + 1 = 9 using the change of base formula, we need to isolate the variable x.
Here are the steps to solve the equation:
Subtract 1 from both sides of the equation:
2x + 1 - 1 = 9 - 1
2x = 8
Divide both sides of the equation by 2:
(2x) / 2 = 8 / 2
x = 4
The solution to the equation 2x + 1 = 9 is x = 4.
The change of base formula is not required to solve this equation since it is a basic linear equation.
To know more about equation,
https://brainly.com/question/29946943
#SPJ11
None of the given options is the correct solution for the equation 2x + 1 = 9 when using the change of base formula. The correct solution for x is x = 4.
To solve the equation 2x + 1 = 9 using the change of base formula, we need to isolate the variable x. Here are the steps to solve it:
Subtract 1 from both sides of the equation to isolate the term with x:
2x + 1 - 1 = 9 - 1
2x = 8
Divide both sides of the equation by 2 to solve for x:
2x/2 = 8/2
x = 4
Now, let's check which option from the given choices gives us x = 4 when applied:
a. x = log(9/2 + 1) / log(2)
Plugging in the values, we get:
x = log((9/2) + 1) / log(2)
x = log(4.5 + 1) / log(2)
x = log(5.5) / log(2)
This option does not give us x = 4.
b. x = log(9/2 - 1) / log(2)
Plugging in the values, we get:
x = log((9/2) - 1) / log(2)
x = log(4.5 - 1) / log(2)
x = log(3.5) / log(2)
This option does not give us x = 4.
c. x = log(9 + 1) / log(2)
Plugging in the values, we get:
x = log(9 + 1) / log(2)
x = log(10) / log(2)
This option does not give us x = 4.
d. x = log(9 - 1) / log(2)
Plugging in the values, we get:
x = log(9 - 1) / log(2)
x = log(8) / log(2)
This option also does not give us x = 4.
Therefore, none of the given options is the correct solution for the equation 2x + 1 = 9 when using the change of base formula. The correct solution for x is x = 4.
To know more about equation,
brainly.com/question/29946943
#SPJ11
What is the y intercept of this graph?. What is the slope?

Answers
Answer:
y intercept is -3
slope is 4
y=4x-3
Step-by-step explanation:
A cylinder has a radius of 3 ft and a height of 5 ft. Find the volume
Answers
Question :-
A Cylinder has a Radius of 3 Ft and a Height of 5 Ft . Find the Volume .Answer :-
Volume of Cylinder is 141.42 Ft³ .Explanation :-
As per the provided information in the given question, we have been given that the Radius of the Cylinder is 3 Ft . The Height is given as 5 Ft . And, we have been asked to calculate the Volume of Cylinder .
For calculating the Volume , we will use the Formula :-
\( \bigstar \: \: \: \boxed{ \sf{ \: Volume \: _{Cylinder} \: = \: \pi {r}^{2}h \: }} \)
Where ,
R denotes to RadiusH denotes to HeightTherefore , by Substituting the given values in the above Formula :-
\( \Longrightarrow \: \: \: \sf { Volume \: _{Cylinder} \: = \: \pi {r}^{2}h } \)
\( \Longrightarrow \: \: \: \sf { Volume \: _{Cylinder} \: = \: \dfrac {22}{7} \: \times \: ({3})^{2} \: \times \: 5 } \\ \)
\( \Longrightarrow \: \: \: \sf { Volume \: _{Cylinder} \: = \: \dfrac {22}{7} \: \times \: 9 \: \times \: 5 } \\ \)
\( \Longrightarrow \: \: \: \sf { Volume \: _{Cylinder} \: = \: \dfrac {22\: \times \: 9 \: \times \: 5 }{7}} \\ \)
\( \Longrightarrow \: \: \: \sf { Volume \: _{Cylinder} \: = \: \dfrac { \: 990 \: }{7}} \\ \)
\( \Longrightarrow \: \: \: \bf { Volume \: _{Cylinder} \: = \: 141.42 } \)
Hence :-
Volume of Cylinder = 141.42 Ft³ .\( \underline {\rule {180pt}{4pt}} \)
Answer:
Volume of cylinder is 141.3 ft³ ( Taking value of π as 3.14 )
Step-by-step explanation:
Question : -A cylinder has a radius of 3 ft and a height of 5 ft. Find the volume .
Given : - Radius of cylinder = 3 ftHeight of cylinder = 5 ft To Find : -We have to , volume of Cylinder .
Formula Used : -\( \boxed{ \sf{Volume \: of \: Cylinder = \pi r {}^{2} h }}\)
Where ,
π = 3.14r = radius of cylinderh = height of cylinder Solution : -\( \longrightarrow \: \pi r {}^{2} h\)
Now , substituting values of radius and height :
\(\longrightarrow \: 3.14 \times (3) {}^{2} \times 5\)
Now , calculating :
\( \longrightarrow 3.14 \times 9 \times5 \)
Firstly , multiplying 9 and 5 :
\(\longrightarrow \: 3.14 \times 45\)
Atlast , multiplying 3.14 and 45 :
\( \longrightarrow \: \bold{ 141.3}\)
\( \red{ \boxed{ \rm{Therefore , \: volume \: of \: cylinder \: is \: 141.3 \: ft {}^{3} }}}\)
#Keep LearningWhat is confounding in statistics?
Answers
HELP ILL GIVE BRAINLIEST

Answers
Answer:
-5/7
Step-by-step explanation:
Do you want one?
Answer: -5/7
Step-by-step explanation:
Jalen earns `\$33` for babysitting `4` hours. At this rate, how much will he earn if he babysits for `7` hours?.
Answers
Answer:
Step-by-step explanation:
If 33/4 is 8.25 dollars, that means in 7 hours he will make on average 57.75 dollars if 8.25 times 7 is 57.75.
f(x)=−x−4, find f(-2)
Answers
By evaluating the function in x = -2, we will get:
f(-2) = -2
How to find f(-2)?To do that, we need to evaluate the given linear equation:
f(x) = -x - 4
We want to find f(-2), so we need to evaluate the linear equation in x = -2, this means that we just need to replace the variable by the corresponding number.
Then we will get:
f(-2) = -(-2) - 4
f(-2) = +2 - 4
f(-2) = -2
Learn more about evaluating functions:
https://brainly.com/question/1719822
#SPJ1
a grey squirrel population was introduced in a certain county of great britain 35 years ago. biologists observe that the population doubles every 7 years, and now the population is 80,000. (a) what was the initial size of the squirrel population? squirrels (b) estimate the squirrel population 12 years from now. (round your answer to the nearest whole number.) squirrels
Answers
The initial size of the population is 2,500 squirrels.
The squirrel population 12 years from now would be 274,286 squirrels.
It has been given in the question that squirrels were introduced in Britain =35 years ago (i)
The population of squirrels doubles every = 7 years (ii)
This means that during this time, the population has doubled = 35/7 = 5 times (iii)
The population now is = 80,000 (iv)
(a) The initial population can be obtained by using the values of (iv) and dividing it by the double five times -
= 80,000 / (2*2*2*2*2)
= 2,500 squirrels in the initial population
(b) If the previous population doubles every seven years.
And every five years, it increases 5/7 * 2 times.
After 12 years it is going to be = (2 +5/7 *2) * 80,000
=(3.42) * 80,000
= 274,286 squirrels
Learn to know more about Population increase on
https://brainly.com/question/27779235?referrer=searchResults
#SPJ4
A baker used c candy eyes to decorate cupcakes. Each cupcake needed 2 candy eyes. Choose the expression that shows how many cupcakes the baker decorated in all.
Answers
The expression that shows how many cupcakes the baker decorated is:
c/2.
What is a mathematical expression?A mathematical expression is a combination of numbers, symbols, and/or variables that represents a mathematical relationship or operation. It can be written using various mathematical symbols and notation to convey a specific meaning or instruction.
Mathematical expressions can also include functions, exponents, logarithms, and other mathematical operations that represent specific relationships or computations. They are commonly used in algebra, calculus, geometry, and other branches of mathematics to represent and solve mathematical problems.
The number of cupcakes the baker decorated can be found by dividing the total number of candy eyes by the number of candy eyes needed per cupcake.
If the baker used c candy eyes in total and each cupcake needed 2 candy eyes, then the expression that shows how many cupcakes the baker decorated is:
c/2
Dividing c by 2 gives the number of cupcakes the baker decorated, since each cupcake required 2 candy eyes.
To know more about exponents, visit:
https://brainly.com/question/5497425
#SPJ1
The number of cupcakes is the total number of candy eyes divided by 2.
What is equation?
A math equation is a method that links two claims and represents equivalence using the equals sign (=). An equation is a mathematical statement that establishes the equivalence of two mathematical expressions in algebra.
The number of cupcakes decorated is equal to the total number of candy eyes divided by the number of candy eyes used per cupcake. So, if c is the number of candy eyes, then the expression that shows how many cupcakes the baker decorated is:
c/2
This is because each cupcake needs 2 candy eyes.
Therefore, the number of cupcakes is the total number of candy eyes divided by 2.
To know more about equation from the given link:
brainly.com/question/649785
#SPJ1
given a student earned an a, what is the chance they attend class regularly? cond - numeric answer .8834 you are incorrect hint: p(r|a) round to four decimal places.
Answers
Answer: Probability that she attended class regularly given that she receives A grade is 0.9286.
Step-by-step explanation: i looked it up man ♀️
Find the exact value of each expression. sin75 degrees and cos(-75 degrees).
Answers
Answer:
0.965925826
0.258819045
Step-by-step explanation:
→If you were to calculate \(sin(75)\), you would have a total of:
0.965925826
→If you were to calculate \(cos(-75)\), you would have a total of:
0.258819045