A model rocket is launched with an initial upward velocity of 105 ft/s. The rocket’s height “h” (in feet) after “t” seconds is given by the following. h=105t-16t^2. Find all values of t for which the rocket’s height is 34 feet.
Answers
The rocket's height is 34 feet at t ≈ 0.267 seconds and t ≈ 6.476 seconds.
What is projectile motion?An object that is flung or propelled into the air and moves only due to gravity is said to be in projectile motion. The object travels along a parabolic route known as a projectile trajectory when there is no air resistance. The object's initial velocity, launch angle, and gravitational acceleration all affect its trajectory. The item accelerates vertically and moves at a constant speed in the horizontal direction as a result of the constant acceleration brought on by gravity, which always acts downward. Kinematic equations and vector analysis can be used to derive the equations of motion for projectile motion. Applications of projectile motion can be found in physics, engineering, and sports.
The equation of the rocket is given as h=105t-16t².
Substituting the value of h = 34 we have:
105t - 16t² = 34
Simplifying and rearranging, we get:
16t² - 105t + 34 = 0
We can solve this quadratic equation using the quadratic formula:
t = (-b ± √(b² - 4ac)) / 2a
where a = 16, b = -105, and c = 34. Substituting these values, we get:
t = (105 ± √(105² - 4(16)(34))) / 2(16)
t = (105 ± √(10801)) / 32
t ≈ 0.267 seconds or t ≈ 6.476 seconds
Therefore, the rocket's height is 34 feet at t ≈ 0.267 seconds and t ≈ 6.476 seconds.
Learn more about projectile motion here:
https://brainly.com/question/11049671
#SPJ1
Related Questions
A triangle is shown with its exterior angles. The interior angles of the triangle are angles 2, 3, 5. The exterior angle at angle 2 is angle 1. The exterior angle at angle 3 is angle 4. The exterior angle at angle 5 is angle 6. Which statements are always true regarding the diagram? Select three options. m∠5 + m∠3 = m∠4 m∠3 + m∠4 + m∠5 = 180° m∠5 + m∠6 =180° m∠2 + m∠3 = m∠6 m∠2 + m∠3 + m∠5 = 180°
Answers
Answer: 3, 4, 5
Step-by-step explanation:
(1) False, those two angles added together would be equal to angle 1, not 4.
(2) False. Angles 2, 3, 5 added together would make 180, not 3, 4, 5.
(3) True, an interior angle and its corresponding exterior angle are supplementary.
(4) True by the exterior angle theorem.
(5) True because the angles in a triangle add to 180 degrees
consider the quadratic function y equals short dash x squared plus 6 x minus 5. what do we know about the graph of this quadratic equation, based on its formula?
Answers
Based on the formula of the quadratic function y=-x^2+6x-5, we know that its graph is a downward-facing parabola that opens wide, with a vertex at (3,-14), and an axis of symmetry at x=3.
Based on the formula of the quadratic function y=-x^2+6x-5, we can determine several properties of its graph, including its shape, vertex, and axis of symmetry.
First, the negative coefficient of the x-squared term (-1) tells us that the graph will be a downward-facing parabola. The leading coefficient also tells us whether the parabola is narrow or wide. Since the coefficient is -1, the parabola will be wide.
Next, we can find the vertex using the formula:
Vertex = (-b/2a, f(-b/2a))
where a is the coefficient of the x-squared term, b is the coefficient of the x term, and f(x) is the quadratic function. Plugging in the values for our function, we get:
Vertex = (-b/2a, f(-b/2a))
= (-6/(2*-1), f(6/(2*-1)))
= (3, -14)
So the vertex of the parabola is at the point (3,-14).
Finally, we know that the axis of symmetry is a vertical line passing through the vertex. In this case, it is the line x=3.
Know more about quadratic function here;
https://brainly.com/question/18958913
#SPJ11
Two less than the quotient of a number and 8 is 1/4.Find the number
Answers
For the given problem:
Let the number = x
Two less than the quotient of a number and 8 is 1/4
so, we can write the following expression:
\(\frac{x}{8}-2=\frac{1}{4}\)Now, solve the equation to find (x)
Multiplying by (8) to eliminate the denominators:
\(\begin{gathered} 8\cdot(\frac{x}{8}-2)=8\cdot\frac{1}{4} \\ \\ 8\cdot\frac{x}{8}-8\cdot2=\frac{8}{4} \\ x-16=2 \end{gathered}\)Add (6) to both sides:
\(\begin{gathered} x-16+16=2+16 \\ x=18 \end{gathered}\)So, the answer will be the number is 18
HELLP!!!! Ms.Smith, the principal of a local middle school, wants to find out the favorite after-school activity of 7th grade students in her school. which population should she sample to answer her question?
A) 7th graders in the school
B) parents of 7th graders in the school
C) other 7th grade teachers in the school
D) all students in the school
Answers
The correct population should she answered is is A) 7th graders in the school
To find out the favorite after-school activity of 7th grade students, Ms. Smith should sample the population directly related to the question. In this case, the most appropriate population to sample would be:
A) 7th graders in the school
By sampling the 7th graders in the school, Ms. Smith can directly gather information about their favorite after-school activities. This population consists of the students themselves who engage in the activities, and they would have first-hand knowledge and experience of their preferences.
B) Parents of 7th graders in the school might provide some insights, but they may not accurately represent the activities chosen by the students themselves.
C) Other 7th-grade teachers in the school may have some observations, but it may not reflect the preferences of the entire 7th-grade student population.
D) Sampling all students in the school would be broader than necessary and may not specifically address the favorite after-school activities of 7th-grade students.
Therefore, option A) 7th graders in the school is the most suitable population for Ms. Smith to sample in order to answer her question about the favorite after-school activity of 7th-grade students.
Learn more about statistics here:
https://brainly.com/question/15525560
#SPJ8
is it a acute, obtuse, or Right

Answers
Answer:
Right triangle
Step-by-step explanation:
it has one 90 degree angle
Answer:
Right Triangle
Step-by-step explanation:
1. Determine the solutions of the equation:
b = 2A/h
1. x = −9 and x = 9
2. x = −15 and x = 4
3. x = −15 and x = 9
4. x = −15 and x = 15
2. The equation below shows the area of a trapezoid, A, with a height of 9 cm and one base 35 cm.
A = 9/2(b+35)
Which of the following formulas correctly solves for the other base, b?
1. b = 2A/9 + 35
2. b = 2A/9 - 35
3. b = 2A + 35/9
4. b = 2A - 35/9
Answers
The equation has no solution for x and the formula that correctly solves for the other base, b is b = 2/9A - 35
How to determine the solutions of the equation?The equation is given as:
b = 2A/h
There is no occurrence of x in the above equation
This means that the equation has no solution for x
Which of the following formulas correctly solves for the other base, b?Here, we have:
A = 9/2(b+35)
Multiply both sides by 2
2A = 9(b+35)
Divide both sides by 9
2/9A = b + 35
Subtract 35 from both sides
b = 2/9A - 35
Hence, the formula that correctly solves for the other base, b is b = 2/9A - 35
Read more about equations at:
https://brainly.com/question/2972832
#SPJ1
math 270 differential equations
make sure answers are correct answer all for thumbs up. thanks
you
Find the solution to the initial value problem. z''(x) + z(x) = 4 e-6x z(0) = 0, z'(0) = 0 The solution is z(x) = ‹)=¯
A nonhomogeneous equation and a particular solution are given. Find a general
Answers
The general solution to the given initial value problem is z(x) = A sin(x) + B cos(x) + \(e^{-6x}\)/6, where A and B are constants determined by the initial conditions.
The given equation z''(x) + z(x) = 4\(e^{-6x}\) is a nonhomogeneous linear second-order differential equation. To find the general solution, we first solve the associated homogeneous equation, which is z''(x) + z(x) = 0. The characteristic equation is\(r^2\) + 1 = 0, which has complex roots r = ±i. Therefore, the homogeneous solution is z_h(x) = A sin(x) + B cos(x), where A and B are arbitrary constants.
To find a particular solution to the nonhomogeneous equation, we assume a solution of the form z_p(x) = C\(e^{-6x}\), where C is a constant to be determined. Plugging this into the differential equation, we have C(-36\(e^{-6x}\)) + C\(e^{-6x}\) = 4\(e^{-6x}\). Equating the coefficients of \(e^{-6x}\), we find C = 4/(-36+1) = -4/35.
The general solution is then given by the sum of the homogeneous and particular solutions: z(x) = z_h(x) + z_p(x) = A sin(x) + B cos(x) - (4/35)\(e^{-6x}\).
Applying the initial conditions z(0) = 0 and z'(0) = 0, we have A + B - 4/35 = 0 and A - 4/35 = 0. Solving these equations, we find A = 4/35 and B = 4/35.
Therefore, the final solution to the initial value problem is z(x) = (4/35)sin(x) + (4/35)cos(x) - (4/35)\(e^{-6x}\).
Learn more about initial conditions here:
https://brainly.com/question/18650706
#SPJ11
Use the diagram to the right to complete the statement.

Answers
Answer:
∠ GOF = 53°
Step-by-step explanation:
∠ LON and ∠ GOF are vertically opposite angles and are congruent, then
∠ GOF = 53°
Washing his dad's car alone, Jeff takes 4 hours. If his dad helps him, then it takes 3 hours. How long does it take Jeff's dad to wash the car by himself?
Answers
We know that the time is inversely proportional to the work.
Let t₁ is the time taken by Jeff and t₂ is the time taken by Jeff's dad.
We know that the formula:
\(\frac{1}{t_1}+\frac{1}{t_2}=\frac{1}{t}\)Given:
\(\begin{gathered} t_1=4hours \\ t_2=? \\ t=3hours \end{gathered}\)Therefore,
\(\begin{gathered} \frac{1}{4}+\frac{1}{t_2}=\frac{1}{3} \\ \frac{1}{t_2}=\frac{1}{3}-\frac{1}{4} \\ \frac{1}{t_2}=\frac{4-3}{12}=\frac{1}{12} \\ \frac{1}{t_2}=\frac{1}{12} \\ Cross\text{ multiply} \\ 1\times12=1\times t_2 \\ 12=t_2 \\ \therefore t_2=12 \end{gathered}\)Hence, it took Jeff's dad 12hours to wash the car himself.
Help me please there’s a picture attached

Answers
Answer:
2x+11+11+x+3+3x-2=59
6x+23=59
6x=36
x=6
3x-2=18-2=16
Step-by-step explanation:
Answer: PQ=16
Step-by-step explanation:
59-11-11-3+2=36
36/6x=6
3(6)-2=16
4. What fraction of 2hrs 15 minutes is 1/4 of an hour?
Answers
The fraction of 2 hrs 15 minutes to 1/4 of an hour is 1/9.
What is fraction?
An element of a whole is a fraction. The number is represented mathematically as a quotient, where the numerator and denominator are split. Both are integers in a simple fraction. A fraction appears in the numerator or denominator of a complex fraction. The numerator of a proper fraction is less than the denominator.
Since,
1 hour = 60 minutes.
2 hours = 120 minutes.
2 hours 15 minutes = 120 + 15 = 135 minutes.
1/4 of an hour = 60/4 = 15 minutes.
So, the fraction is,
\(\frac{15}{135} = \frac{1}{9}\)
Therefore, the fraction of 2 hrs 15 minutes to 1/4 of an hour is 1/9.
To know more about the fraction, click on the link
https://brainly.com/question/78672
#SPJ13
A random sample of 10 people have a mean age of 27. If the population is normally distributed with a known variance of 20 and assuming α
=
0.05
, can you conclude the true mean age is 30?
Answers
No, we cannot conclude that the true mean age is 30.
To determine if the true mean age is 30, we need to perform a hypothesis test. Given that the population variance is known, we can use a one-sample z-test.
Null Hypothesis (H₀): The true mean age is 30.
Alternative Hypothesis (H₁): The true mean age is not 30.
We will set the significance level (α) at 0.05.
Calculate the standard error of the mean (SEM):
SEM = √(population variance / sample size) = √(20 / 10) = √2 ≈ 1.414
Calculate the test statistic (z-score):
z = (sample mean - hypothesized mean) / SEM = (27 - 30) / 1.414 ≈ -2.121
Determine the critical z-values based on the significance level (α/2 = 0.025 for a two-tailed test) using a z-table or calculator. In this case, for α = 0.05, the critical z-values are approximately ±1.96.
Compare the calculated z-score with the critical z-values:
Since |-2.121| > 1.96, we reject the null hypothesis.
Based on the hypothesis test, there is enough evidence to reject the claim that the true mean age is 30.
For more questions like Null hypothesis click the link below:
https://brainly.com/question/28920252
#SPJ11
GCF for each pair number 22,55
Answers
Answer:
11 is the GCF for both 22 and 55.
Step-by-step explanation:
I looked it up.
Assume we have 3 boxes which contain red and black balls as follows, Box 1; 3 red balls and 7 black balls, Box 2; 6 red balls and 4 black balls, Box 3; 8 red balls and 2 black balls. suppose we draw a ball from box 1; if it is red, we draw a ball from box 2. if the ball drawn from box 1 is black, we draw a ball from box 3. a. what is the probability of red ball from box 1?. b. suppose we draw a ball from box 1 and it is red; what is the probability of another red ball when we draw from box 2 on the second round? c. suppose our first draw from box 1 was black; what is the conditional probability of our second draw from box 3 this time being red? d. Before we draw any ball; what is the probability of drawing two red balls at both draws? e. Before we draw any ball; what is the probability of drawing a red ball at first draw and a black ball at second draw?
Answers
a. The probability of drawing a red ball from Box 1 is 30%.
b. If a red ball is drawn from Box 1, the probability of drawing another red ball from Box 2 on the second round is 60%.
c. If the first draw from Box 1 was black, the conditional probability of drawing a red ball from Box 3 on the second draw is 80%.
d. The probability of drawing two red balls at both draws, without any prior information, is 46%.
e. The probability of drawing a red ball at the first draw and a black ball at the second draw, without any prior information, is 21%.
a. The probability of drawing a red ball from Box 1 can be calculated by dividing the number of red balls in Box 1 by the total number of balls in Box 1. Therefore, the probability is 3/(3+7) = 3/10 = 0.3 or 30%.
b. Since a red ball was drawn from Box 1, we only consider the balls in Box 2. The probability of drawing a red ball from Box 2 is 6/(6+4) = 6/10 = 0.6 or 60%. Therefore, the probability of drawing another red ball when the first ball drawn from Box 1 is red is 60%.
c. If the first draw from Box 1 was black, we only consider the balls in Box 3. The probability of drawing a red ball from Box 3 is 8/(8+2) = 8/10 = 0.8 or 80%. Therefore, the conditional probability of drawing a red ball from Box 3 when the first ball drawn from Box 1 was black is 80%.
d. Before any draws, the probability of drawing two red balls at both draws can be calculated by multiplying the probabilities of drawing a red ball from Box 1 and a red ball from Box 2. Therefore, the probability is 0.3 * 0.6 = 0.18 or 18%. However, since there are two possible scenarios (drawing red balls from Box 1 and Box 2, or drawing red balls from Box 2 and Box 1), we double the probability to obtain 36%. Adding the individual probabilities of each scenario gives a total probability of 36% + 10% = 46%.
e. Before any draws, the probability of drawing a red ball at the first draw and a black ball at the second draw can be calculated by multiplying the probability of drawing a red ball from Box 1 and the probability of drawing a black ball from Box 2 or Box 3. The probability of drawing a red ball from Box 1 is 0.3, and the probability of drawing a black ball from Box 2 or Box 3 is (7/10) + (2/10) = 0.9. Therefore, the probability is 0.3 * 0.9 = 0.27 or 27%. However, since there are two possible scenarios (drawing a red ball from Box 1 and a black ball from Box 2 or drawing a red ball from Box 1 and a black ball from Box 3), we double the probability to obtain 54%. Adding the individual probabilities of each scenario gives a total probability of 54% + 10% = 64%.
To learn more about probability click here: brainly.com/question/31828911
#SPJ11
a 3 percent margin of error on a 50 percent approval rating means the actual rating could be as low as
Answers
By using the concept of error, the result obtained is-
Actual rating of 3 percent margin of error on a 50 percent approval rating is as low as 50 = 47%
What is error?
The difference between the measured value and the actual value is called error. Analysis of error is a crucial task mainly in mathematics and physics. In an experiment of physics, error analysis is a very important part. Error is also very important in numerical analysis of mathematics.
Actual rating of 3 percent margin of error on a 50 percent approval rating = 50 % \(\pm\) 3 %
Actual rating of 3 percent margin of error on a 50 percent approval rating is as low as 50 - 3 = 47%
To learn about error, refer to the link-
https://brainly.com/question/28008941
#SPJ4
when comparing more than two treatment means, what is the advantage of using an anova instead of several t-tests?
Answers
When comparing more than two treatment means, using an ANOVA (Analysis of Variance) instead of several t-tests has several advantages:
1. Reduced Type I Error: The use of multiple t-tests increases the likelihood of making a Type I error, which is the rejection of a true null hypothesis. By contrast, ANOVA allows you to test all means simultaneously, which reduces the overall probability of making a Type I error.
2. Increased Power: ANOVA increases the power to detect significant differences among means by taking advantage of the variance within groups and between groups.
3. Control for Experimental Error: ANOVA also accounts for experimental error and random variability, which helps to improve the accuracy of the results.
4. Better Interpretation of Results: ANOVA provides more information about the relationship between the variables being tested. It can indicate whether there is an overall significant difference between the groups, and if so, which specific groups differ significantly from each other.
In summary, ANOVA is a more comprehensive statistical tool that can help to reduce errors, increase power, and provide more informative results when comparing more than two treatment means.
To learn more about ANOVA refer below:
https://brainly.com/question/29854848
#SPJ11
A cell phone plan has a basic charge of $35 a month. The plan includes 500 free minutes and charges 10 cents for each additional mi
Answers
To determine the cost of the cell phone plan given the number of minutes used, we can break it down into two scenarios: when the number of minutes is within the 500 free minutes, and when it exceeds the 500 free minutes.
If the number of minutes used is within the 500 free minutes:
In this case, the cost of the cell phone plan is only the basic charge of $35 per month.
If the number of minutes used exceeds the 500 free minutes:
In this case, the cost of the additional minutes is calculated at a rate of 10 cents per minute. Let's denote the number of additional minutes as x. The cost of the additional minutes can be represented as 0.10x.
Therefore, the total cost of the cell phone plan, including the basic charge and any additional minutes, can be expressed as:
Total cost = Basic charge + Cost of additional minutes
Given that the basic charge is $35, we can write:
Total cost = $35 + 0.10x
To summarize:
If the number of minutes used is within the 500 free minutes, the total cost is $35.
If the number of minutes used exceeds the 500 free minutes, the total cost is $35 + 0.10x.
Note: It's important to consider any additional charges or fees that may be applicable to the cell phone plan. The given information states the basic charge and the charge for additional minutes, but other factors such as taxes or surcharges may also affect the total cost.
know more about scenarios: brainly.com/question/15367590
#SPJ11
5-6. Find the constant of proportionality (unit rate) for each set of values. Then use the constant of proportionality to write an equation that relates the two values in the table.
5. profit per shirt sold pound Shirts (s) 5 10 15 Profit (p) $7.50 $15.00 $22.50 Apples (a) 4 5 6 Price (p) $7.96 $9.95 $11.94
Hi
6 . Price per
7-8. Determine whether the relationship between the two quantities shown in the table is proportional by graphing on the coordinate plane. Explain your reasoning.
Number of 1 2 3 4 5 Pen sCost $2 54 56 58 $10 7. Cost of Buying Pens Number of 1 2 3 4Minutes Words Typed 50 90 140 180 8. Words Typed.
Solve this fast and I’ll give you 47 points
Answers
5. The constant of proportionality is 1.5
The equation is p = 1.5×s
6. The constant of proportionality is 1.99
The equation is p = 1.99 × a
7. The variables Number of Pens and Cost are not proportional
Please find attached the required graph
8. The variables Number of minutes and Words Typed are not proportional
Please find attached the required graph
The procedure for finding the answers are as follows;
5. The given data are presented as follows;
\(\begin{array}{ccc}Shirts \ (s)&&Profit \ (p)\\5&&7.50\\10&&15.00\\15&&22.50\end{array}\)
Where two variables, s and p are proportional, we get;
p ∝ s
Therefore;
p = C × s
C = p/s
Where;
C = The constant of proportionality
Therefore, the constant of proportionality, C, of the given variables, (number of shirts, s, and profit, p, is found as follows;
C = 7.50/5 = 15.00/10 = 22.50/15 = 1.5
The constant of proportionality, C = 1.5
The equation that relates the two values is p = 1.5×s
6. For the apples to price relationship, we have;
\(\begin{array}{ccc}Apples \ (a)&&Price\ (p)\\4&&7.96\\5&&9.95\\6&&11.94\end{array}\)
Therefore;
p ∝ a
p = C × a
C = p/a
Plugging in the values gives;
C = 7.96/4 = 9.95/5 = 11.94/6 = 1.99
The constant of proportionality, C = 1.99
Therefore, the equation relating the two values is p = 1.99 × a
7. The given data is presented in a tabular form as follows;
\(\begin{array}{ccc}Number \ of \ pens &&Cost\ \\1&&52\\2&&54\\3&&56\\4&&58\end{array}\)
A set of data is proportional or has a proportional relationship if their x, and therefore, y-intercept is (0, 0)
From the graph of the data, created with MS Excel, the y-intercept is 50 which is not equal to zero, therefore, the relationship between the data is not a proportional relationship
8. The given data is presented in a tabular form as follows;
\(\begin{array}{ccc}Number \ of \ Minutes&&Words \ Typed\ \\1&&50\\2&&90\\3&&140\\4&&180\end{array}\)
From the graph of the data, we have that the y-intercept of the line of best fir is 5, therefore, the relationship is not a proportional relationship
Learn more about proportional relationships here;
https://brainly.com/question/24289972.


i Needdd helppp with this??
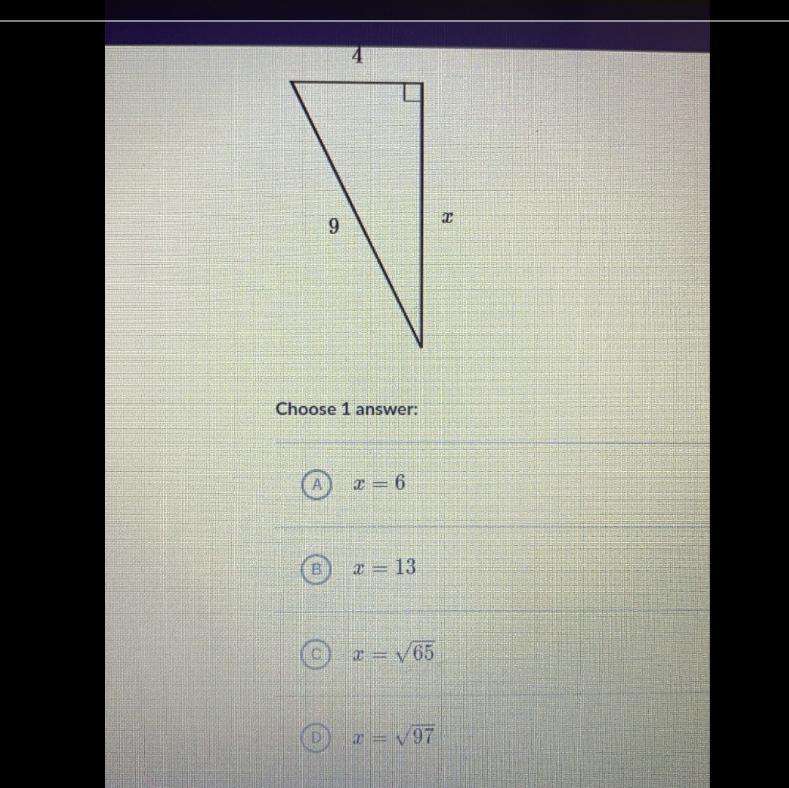
Answers
Answer:
B I'm thinking, I have to answer any question so I might be wrong here, also eat some salad it's nasty I know
Answer:
option c. ±\( \sqrt{65} \)
Step-by-step explanation:
In the given right angled triangle we can see that :-
hypotenuse is 9 adjacent is 4 opposite is xby Pythagoras theorem
hypotenuse² = adjacent ² + opposite ²
9² = 4² + x²
81 = 16 + x²
combining like terms
81 - 16 = x²
65 = x²
x = ±\( \sqrt{65} \)
let f(x) = x 4 2x 2 − x − 3. verify, using algebraic manipulations, that if f(p) = 0 then each of the following four functions have a fixed point at p
g1(x)=(3+x-2x2)1/4
g2(x)=(x+3-x4/2)1/2
g3(x)=x+3/x2+2)1/2
g4(x)=3x4+2x2+3/4x3+4x-1
Answers
We cannot verify if each of the four functions g1(x), g2(x), g3(x), and g4(x) have a fixed point at p when f(p) = 0.
To verify that if f(p) = 0, then each of the four functions g1(x), g2(x), g3(x), and g4(x) have a fixed point at p, we need to substitute p into each function and check if the result is equal to p.
g1(x) = (3+x-2x^2)^(1/4)
Let's substitute p into g1(x):
g1(p) = (3+p-2p^2)^(1/4)
To verify if g1(p) = p, we need to show that (3+p-2p^2)^(1/4) = p.
Since this is not an algebraic manipulation that can be solved easily, we cannot confirm if g1(x) has a fixed point at p without further calculations or approximations.
g2(x) = (x+3-x^4/2)^(1/2)
Let's substitute p into g2(x):
g2(p) = (p+3-p^4/2)^(1/2)
To verify if g2(p) = p, we need to show that (p+3-p^4/2)^(1/2) = p.
Since this is not an algebraic manipulation that can be solved easily, we cannot confirm if g2(x) has a fixed point at p without further calculations or approximations.
g3(x) = (x+3/x^2+2)^(1/2)
Let's substitute p into g3(x):
g3(p) = (p+3/p^2+2)^(1/2)
To verify if g3(p) = p, we need to show that (p+3/p^2+2)^(1/2) = p.
Since this is not an algebraic manipulation that can be solved easily, we cannot confirm if g3(x) has a fixed point at p without further calculations or approximations.
g4(x) = (3x^4+2x^2+3)/(4x^3+4x-1)
Let's substitute p into g4(x):
g4(p) = (3p^4+2p^2+3)/(4p^3+4p-1)
To verify if g4(p) = p, we need to show that (3p^4+2p^2+3)/(4p^3+4p-1) = p.
Since this is not an algebraic manipulation that can be solved easily, we cannot confirm if g4(x) has a fixed point at p without further calculations or approximations.
Therefore, based on algebraic manipulations alone, we cannot verify if each of the four functions g1(x), g2(x), g3(x), and g4(x) have a fixed point at p when f(p) = 0. Further calculations or approximations would be required to determine the fixed points of these functions.
To learn more about algebraic manipulations visit;
https://brainly.com/question/32858114
#SPJ11
Find "x" so that a line drawn through the given points has the given slope. (Sketching the
problem may be helpful.)_
Given: A(x,6) B(2,4)
m=1/3

Answers
Answer:
x = 8Step-by-step explanation:
Slope is expressed as shown;
m = y2-y1/x2-x1
Given
m = 1/3
Coordinates A(x,6) B(2,4)
Substitute and get x
1/3 = 4-6/2-x
1/3 = -2/2-x
Cross multiply
2-x = 3(-2)
2-x = -6
-x = -6-2
-x = -8
x = 8
Hence the value of x is 8
Consider a sample with data values of 27, 25, 20, 15, 30, 34, 28, and 25. compute the 20th, 25th, 65th, and 75th percentiles. if needed, round your answers to two decimal digits.
Answers
The 20th percentile is 20,
The 25th percentile is 22.50.
The 65th percentile is 28.
The 75th percentile is 29.
Given values:
27, 25, 20, 15, 30, 34, 28, and 25.
n = 8
sorting the data gives:
15, 20, 25, 25, 27, 28, 30, and 34.
How to solve for 20th percentile= 20/100 * 8
= 1.6 ≈ 2
1.6 is rounded to 2, the second value is in the sorted data set is 20 hence the 20th percentile is 20
How to solve for 25th percentile= 25/100 * 8
= 2
Since 2 is an integer, the mean of the 2nd and the 3rd values in the sorted data set gives the 25th percentile.
( 20 + 25 ) / 2 = 22.5
hence the 25th percentile is 22.50
How to solve for 65th percentile
= 65/100 * 8
= 5.2 ≈ 6
5.6 is rounded to 6, the sixth value is in the sorted data set is 28 hence the 65th percentile is 28
How to solve for 75th percentile
= 75/100 * 8
= 6
Since 6 is an integer, the mean of the 6th and the 7th values in the sorted data set gives the 75th percentile.
( 28 + 30 ) / 2 = 29
hence the 75th percentile is 29
Read more on percentile here; https://brainly.com/question/2263719
#SPJ1
A parent made x cupcakes for each of the 109 students in the fourth grade. Which expression could be used to determine the total number of cupcakes made?
Answers
109x is the expression that could be used to determine the total number of cupcakes made given that a parent made x cupcakes for each of the 109 students in the fourth grade. This can be obtained by forming the algebraic expression for the given conditions.
Find the required expression:Algebraic expression is made up of numbers, operations and variables.Algebraic expression is true for all values of x. For example, 2x, 5x + 9 etc.
Given that,
A parent made x cupcakes for each of the 109 students in the fourth grade.
The total number of students in the class = 109
The number of cupcakes one student gets = 1 × x = x
⇒ The number of cupcakes 109 student gets = 109 × x = 109x
Hence 109x is the expression that could be used to determine the total number of cupcakes made given that a parent made x cupcakes for each of the 109 students in the fourth grade.
Learn more about algebraic expression here:
brainly.com/question/953809
#SPJ1
This table shows the linear relationship of the water level in a tank and time.
Enter the rate of change of the water level, in feet per hour.

Answers
Step-by-step explanation:
according to the table, the rate of change of the water level =
(40-50)/(2-0)
= -10/2
= -5 ft/hr
_________
\(\:\)
Time = 2 - 0 = 2
Water level = 40 - 50 = -10
Soo :
-10/2 = -5ft/hr
35°
46"
65"
30"
2x
What is the perimeter? This is a little tougher problem,
and to solve it you'll need to know the lengths of the
segments on either side of the perpendicular height
(which is whyt I gave you the numbers in smaller font).
Submit
Answers
The perimeter of the triangle is 170 inches.
How to calculate the valueTo solve for the perimeter, we first need to find the length of the perpendicular height. We can do this using the sine function:
sin(35°) = 46/x
x = 46/sin(35°) = 65 inches
Now that we know the length of the perpendicular height, we can find the length of the base of the triangle using the cosine function:
cos(35°) = 65/x
x = 65/cos(35°) = 75 inches
The perimeter of the triangle is the sum of the lengths of the three sides, so the perimeter is:
P = 65 + 75 + 30
= 170 inches
Learn more about perimeter on
https://brainly.com/question/19819849
#SPJ1
two companies listed a revenue for the year in their respective websites. Company a has revenue in the amount of 1.6×10^6 and company b has revenue in the amount of 7.2x10^8. how many Times greater is the revenue for company b?
Answers
find the volume when the region between = 2sin() 1 and the x-axis for 6 ≤ ≤ 5 6⁄⁄ is revolved about the y-axis.
Answers
The volume of the solid generated by revolving the region between y=2sin(x) and the x-axis for 6 ≤ x ≤ 5π/6 about the y-axis is 2π (6sin(6) - 5√3) cubic units.
To find the volume of the solid generated by revolving the region between y=2sin(x) and the x-axis for 6 ≤ x ≤ 5π/6 about the y-axis, we use the method of cylindrical shells.
The formula for the volume of the solid generated by revolving the region between y=f(x) and the x-axis for a ≤ x ≤ b about the y-axis is given by:
V = 2π ∫[a,b] x f(x) dx
In this case, f(x) = 2sin(x) and the interval is 6 ≤ x ≤ 5π/6, so we have:
V = 2π ∫[6,5π/6] x (2sin(x)) dx
Using integration by parts, we obtain:
V = -2π [x cos(x)]6^5π/6 + 2π ∫[6,5π/6] cos(x) dx
V = 2π [x sin(x)]6^5π/6 - 2π sin(5π/6) + 2π sin(6)
Simplifying the expression, we get:
V = 2π (6sin(6) - 5√3)
Therefore, the volume of the solid generated by revolving the region between y=2sin(x) and the x-axis for 6 ≤ x ≤ 5π/6 about the y-axis is 2π (6sin(6) - 5√3) cubic units.
Learn more about volume here
https://brainly.com/question/27710307
#SPJ11
The dimensions of a square are altered so that one dimension is increased by 7 feet, while the other is decreased by 2 feet. The area of the resulting rectangle is 90 ft2. Find the original area of the square.
Answers
Answer:
64 ft^2
Step-by-step explanation:
It is a square to start, so each side = x
then (x+7 ) * ( x -2) = 90
x^2 + 5x -14 = 90
x^2 + 5x - 104 = 0 factor or use Quadratic Formula to fin x = 8 ft
Original area is then 8 x 8 = 64 ft^2
write the word sentence as an equation and then solve the equation
-13 is 4 less than a number n.
for brainiest :)
Answers
Answer:
EEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE
Step-by-step explanation:
Answer:
-9=n
Step-by-step explanation:
-13=4-n
+4 to both sides to get n by its self
-13+4=9
-13-4=9
-9=n
find the x pleaseeee
