A pair of shoes is regularly priced at $80 and is on sale for 20% off. You have a coupon to receive an additional 15% off the sale price. How much will you pay for the shoes?
Answers
The customer would pay $54.40 for the shoes
What is the dollar value of the initial discount of 20%?
The dollar worth of the general discount of 20% of the price of $80 is determined as 20% multiplied by the shoe price
dollar worth of initial discount=20%*$80
dollar worth of the initial discount=$16
the price after the initial discount=$80-$16
the price after the initial discount=$64
The fact the customer has a coupon to receive additional 15% off the sale price means the purchase price for the customer is as computed thus:
final sale price=$64*(1-15%)
final sale price=$54.40
Find out more about discounted price on:https://brainly.com/question/880274
#SPJ1
Related Questions
(
\( \sqrt{2 - 1( \sqrt{2 + 3} } \)
(
Answers
![([tex] \sqrt{2 - 1( \sqrt{2 + 3} } [/tex](](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/V7B9HcFQMfTjcMGjWjBt2qSDsTzh65u3.png)
amara finds the sum of two number cubes rolled at the same time. The chart below shows all possible sums from the 36 possible combinations when rolling two number cubes. How many times should Tamara expect the sum of the two cubes be equal to if she rolls the two number cubes 180 times?
Answers
Tamara should expect the sum of the two cubes to be equal to 7 around 30 times when rolling the two number cubes 180 times.
To determine how many times Tamara should expect the sum of the two number cubes to be equal to a certain value, we need to analyze the chart and calculate the probabilities.
Let's examine the chart and count the number of times each sum occurs:
Sum: 2, Occurrences: 1
Sum: 3, Occurrences: 2
Sum: 4, Occurrences: 3
Sum: 5, Occurrences: 4
Sum: 6, Occurrences: 5
Sum: 7, Occurrences: 6
Sum: 8, Occurrences: 5
Sum: 9, Occurrences: 4
Sum: 10, Occurrences: 3
Sum: 11, Occurrences: 2
Sum: 12, Occurrences: 1
Now, let's calculate the probabilities of each sum occurring.
Since there are 36 possible combinations when rolling two number cubes, the probability of each sum is the number of occurrences divided by 36:
Probability of sum 2 = 1/36
Probability of sum 3 = 2/36
Probability of sum 4 = 3/36
Probability of sum 5 = 4/36
Probability of sum 6 = 5/36
Probability of sum 7 = 6/36
Probability of sum 8 = 5/36
Probability of sum 9 = 4/36
Probability of sum 10 = 3/36
Probability of sum 11 = 2/36
Probability of sum 12 = 1/36
To find out how many times Tamara should expect a certain sum when rolling the two number cubes 180 times, we can multiply the probability of that sum by 180.
For example, to find the expected number of times the sum is 7:
Expected occurrences of sum 7 = (6/36) \(\times\) 180 = 30
Similarly, we can calculate the expected occurrences for all other sums.
For similar question on probabilities.
https://brainly.com/question/30768613
#SPJ8
need some help with these!!

Answers
Explanation: just divide by 2
Because triangle A is double the size of triangle D
32/2 =16
40/2 = 20
48/2 = 24
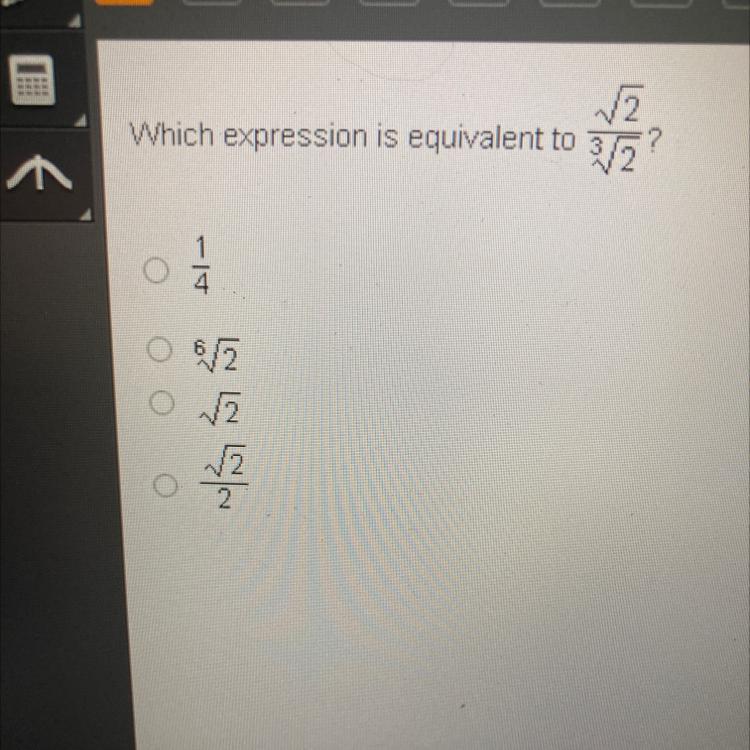
Which expression is equivalent to v2/3v2? 1/4 6v2 v2 v2/2
Answers
Answer:
Step-by-step explanation:
\(2^{1/2} - 2^{-1/3} = 2^{1/2 + 1/3} = 2^{3/6} = 2^{1/2} = \sqrt{2}\)
Answer:
\(\sqrt[6]{2}\)
Step-by-step explanation:
2 ^ 1/2 ÷ 2 ^ 1/3
We know that a^b ÷ a^ c = a^(b-c)
2 ^ (1/2 -1/3)
2^ (3/6 - 2/6)
2 ^ 1/6
\(\sqrt[6]{2}\)
Is 3 the coefficient of s/3?
Answers
The coefficient of s/3 is 1/3.
s/3 = (1/3)s
No, 3 is not the coefficient of s/3.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
s/3
This can be written as (1/3)s.
The coefficients of an equation are the non-zero values along with the variables.
Example:
ax² + bx + 3
The coefficients of this equation are a, and b.
The coefficient for the expression s/3 is 1/3.
Thus,
The coefficient of s/3 is 1/3.
s/3 = (1/3)s
No, 3 is not the coefficient of s/3.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ2
a fast food chain surveyed a random sample of students to determine what pizza they prefer. Based on the results, how many of the 340 students can be expected to prefer cheese pizza?
Answers
A line to vote is moving at a rate of 5 feet every 20 minutes. At this rate, how long has a voter been in line for if they moved 30 feet?
Answers
In order to solve for time, we will solve as follows:
We multiply the movement in the time we want to know (30 ft) times the time it takes to move 5 ft (20 min) and divide it by the 5 ft, that is:
\(t=\frac{30\cdot20}{5}\Rightarrow t=120\)From this, we know it took the voter 120 minutes to move 30 ft.
Write 5/6% as a decimal number.
Answers
Answer: 5/6 as a decimal is 0.833
Step-by-step explanation:
just divide 5 by 6
1.
Which of the following is a quadratic function?
(1) y = 2x + 7
(3) y = x' + 3x2 – 2x +1
(2) y = x2-1
(4) y = 2*
Answers
the answer is 3 hopw this helps
Help pleaseeeeeeeeeeeeee

Answers
Answer: f(8) = 620.6
Step-by-step explanation:
To solve, you must first use substitution, and replace the x value in the given function, with 8.
\(f(8)=\frac{750}{1 + 74e^{-0.734(8)} }\)
Next you follow PEMDAS to solve the rest of the equation to find f(8).
What is PEMDAS?
PEMDAS is the order of operations for mathematical expressions involving more than one operation.
You solve in the following order
P = ParenthesisE = ExponentsM = MultiplicationD = DivisionA = AdditionS = SubtractionIn this case our next step is deal with the exponents.
And by doing so, you will be multiplying -0.734 by 8
\(f(8)=\frac{750}{1 + 74e^{-5.872} }\)
And typical with exponents we would raise the number or variable given to the power of the exponent.
However we have a continuous number in this case, which is e.
What is e?
e is a mathematical constant approximately equal to 2.71828
We can now use a calculator to find what e (2.71....) is when raise to the exponent -5.872. Which results to 0.002817 (0.0028172332293320237716146943697).
When continuing to use numbers in calculators, don't use the rounded or shortened of the full number. Make sure to use the all of the numbers (given in the calculator) to its full extent to maintain accuracy.
\(f(8)=\frac{750}{1 + 74(0.002817) }\)
Now multiply 74 and 0.002817.... (use the full number to multiply (0.0028172332293320237716146943697)). The product is (0.2084752589705697590994873833578).
\(f(8)=\frac{750}{1 + 0.2084 }\)
Now lets add 1 + 0.2084.... and you get 1.2084
\(f(8)=\frac{750}{1.2084 }\)
Last you need to divide:
and you get that
f(8) = 620.6167
Now lets go back to the question, and we see that is says for you to round your answer to the nearest tenth.
so your final answer is:
f(8) = 620.6
Solve for x. 11=3+4x
Answers
To solve for x, we need to isolate the variable (x) on one side of the equation. We can do that by first subtracting 3 from both sides of the equation to get:
11 - 3 = 4x
Simplifying the left side gives:
8 = 4x
Finally, dividing both sides by 4 gives:
x = 2
Therefore, the solution to the equation 11=3+4x is x=2.
the solution to the equation \(11=3+4x\) 11=3+4x is \(x = 2\) X = 2.
The equation \(11=3+4x\) 11=3+4x is a linear equation in one variable \((x)\)(x) with coefficients and constants that are real numbers.
It can be simplified by performing basic algebraic operations, such as isolating the variable term \((4x)\) (4x) and solving for the value of \(x\) x.
to solve for x in the equation \(11=3+4x\) 11=3+4x, we will follow the steps of algebraic manipulation:
First, we will isolate the variable term \((4x)\) (4x) by subtracting 3 from both sides of the equation:
\(11 - 3 = 4x\) 11 - 3 = 4x
\(8 = 4x\) 8 = 4x
Next, we will isolate x by dividing both sides by 4:
\(8/4 = x\) 8/4 = x
\(2 = x\) 2 = x
Therefore, the solution to the equation \(11=3+4x\) 11=3+4x is \(x=2\) x=2.
To know more about linear equations in one variable (x) with coefficients and constants that are real numbers:
https://brainly.com/question/19383157
https://brainly.com/question/19383157
There are 32 chickens and 12 sheep on a farm. The ratio of sheep to horses is 4:1. Write a ratio expressing the relationship between the chicken and the sheep. Then explain what that ratio means. Determine the number of horses on the farm.
Answers
This means that for every 1 sheep on the farm, there are 0.25 horses. To find the total number of horses, we can multiply the number of sheep by 0.25:
\(12 * 0.25 = 3\)
What is ratio?Ratio refers to the quantitative relationship between two or more quantities, expressing the proportion of one quantity to the other(s). It is typically expressed as a fraction, where the numerator represents one quantity, and the denominator represents the other quantity.
For example, the ratio of the number of boys to the number of girls in a class of 30 students might be expressed as 2:3, which means there are 20 girls and 10 boys in the class. Similarly, the ratio of the length to the width of a rectangle might be expressed as 4:3, indicating that the length is four times greater than the width.
The ratio of sheep to horses is 4:1, which means that for every 4 sheep on the farm, there is 1 horse. We can also say that the total ratio of sheep and horses on the farm is 4+1=5.
To express the relationship between the chickens and the sheep, we need to use the fact that there are 32 chickens and 12 sheep on the farm. We can write this as a ratio:
\(chickens : sheep = 32 : 12\)
We can simplify this ratio by dividing both sides by 4:
\(chickens: sheep = 8: 3\)
This means that for every 8 chickens on the farm, there are 3 sheep.
To determine the number of horses on the farm, we can use the fact that the total ratio of sheep and horses is 5. We know that the ratio of sheep to horses is 4:1, so we can write:
\(sheep : horses = 4 : 1\)
We can simplify this ratio by dividing both sides by 4:
\(sheep : horses = 1 : 0.25\)
This means that for every 1 sheep on the farm, there are 0.25 horses. To find the total number of horses, we can multiply the number of sheep by 0.25:
\(12 * 0.25 = 3\)
To know more about denominator, visit:
https://brainly.com/question/17153086
#SPJ1
4. Hydrocarbons in the cab of an automobile were measured during trips on the New Jersey Turnpike and trips through the Lincoln Tunnel connecting New York and New Jersey. The concentrations (± standard deviations) of m- and p-xylene were: Turnpike: 31.4 ± 30.0 g/m3 (32 measurements) Tunnel: 52.9 ± 29.8 g/m3 (32 measurements) Do these results differ at the 95% confidence level?
Answers
Answer:
No these these result do not differ at 95% confidence level
Step-by-step explanation:
From the question we are told that
The first concentrations is \(c _1= 30.0 \ g/m^3\)
The second concentrations is \(c _2 = 52.9 \ g/m^3\)
The first sample size is \(n_1 = 32\)
The second sample size is \(n_2 = 32\)
The first standard deviation is \(\sigma_1 = 30.0 \)
The first standard deviation is \(\sigma_1 = 29.0 \)
The mean for Turnpike is \(\= x _1 = \frac{c_1}{n} = \frac{31.4}{32} = 0.98125\)
The mean for Tunnel is \(\= x _2 = \frac{c_2}{n} = \frac{52.9}{32} = 1.6531\)
The null hypothesis is \(H_o : \mu _1 - \mu_2 = 0\)
The alternative hypothesis is \(H_a : \mu _1 - \mu_2 \ne 0\)
Generally the test statistics is mathematically represented as
\(t = \frac{\= x_1 - \= x_2}{ \sqrt{\frac{\sigma_1^2}{n_1} +\frac{\sigma_2^2}{n_2} }}\)
\(t = \frac{0.98125 - 1.6531}{ \sqrt{\frac{30^2}{32} +\frac{29^2}{32} }}\)
\(t = - 0.0899\)
Generally the degree of freedom is mathematically represented as
\(df = 32+ 32 - 2\)
\(df = 62\)
The significance \(\alpha\) is evaluated as
\(\alpha = (C - 100 )\%\)
=> \(\alpha = (95 - 100 )\%\)
=> \(\alpha =0.05\)
The critical value is evaluated as
\(t_c = 2 * t_{0.05 , 62}\)
From the student t- distribution table
\(t_{0.05, 62} = 1.67\)
So
\(t_c = 2 * 1.67\)
=> \(t_c = 3.34\)
given that
\(t_c > t\) we fail to reject the null hypothesis so this mean that the result do not differ
Sarah loaded 4 trucks in 15 minutes. At that rate, how many trucks would she load in 5 hours?
Answers
4 x 4 = 16
she can load 16 trucks in an hour.
A group of scientists are doing a study of elephants in Africa. They take a random sample of 200 elephants, and reveal the data set below. They believe the population of elephants in the area is about 6 times the size of the random sample. What is the estimated total population of male elephants with tusks?
Answers
Answer:
138
Step-by-step explanation:
Answer: 138
Step-by-step explanation:
-1000 2/3 is not real fraction. True or false
Answers
True, While "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
The statement "-1000 2/3 is not a real fraction" is true. A real fraction is a mathematical expression that represents a ratio of two real numbers. In a fraction, the numerator and denominator are both real numbers, and they can be positive, negative, or zero.
In the given statement, "-1000 2/3" is not a valid representation of a fraction. The presence of a space between "-1000" and "2/3" suggests that they are separate entities rather than being part of a single fraction.
To represent a mixed number (a whole number combined with a fraction), a space or a plus sign is typically used between the whole number and the fraction. For example, a valid representation of a mixed number would be "-1000 2/3" or "-1000 + 2/3". However, without the proper formatting, "-1000 2/3" is not considered a real fraction.
It's important to note that "-1000 2/3" can still be expressed as an improper fraction. To convert it into an improper fraction, we multiply the whole number (-1000) by the denominator of the fraction (3) and add the numerator (2). The result would be (-1000 * 3 + 2) / 3 = (-3000 + 2) / 3 = -2998/3.
In conclusion, while "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
for more such question on fraction visit
https://brainly.com/question/30122573
#SPJ8
Which sports location had the largest increase in the attendance in month 1 to the attendance in month 7?

Answers
For this problem, we are given the attendance graph of three sports centers in the span of 7 months. We need to identify which of the three centers had the largest increase in attendance during this time.
To solve the problem, we need to compare the attendance of each sports center in month 7 with their attendance in month 1.
The Coors field seems to have a growth in attendance of 2.5 horizontal bars, the Petco Park seems to have a growth in attendance of 4.8 bars and the Turner field seems to have a growth in attendance of 3.9 bars. With thi,s we conclude that Petco Park saw the highest growth in attendance.
The answer is Petco Park.
A sequence consists of all 4 digits integers ending in 5 in increasing order

Answers
Digits if four integers.
Formula: 1005 + 10n, n could be 1 , 2, 3 , 4 , etc
S1 = 1005 + 10(1) = 1005 + 10 = 1015
S2 = 1005 + 10(2) = 1005 + 20 = 1025
S3 = 1005 + 10(3) = 1005+ 30 = 1035
S4 = 1005 + 10(4) = 1005 + 40 = 1045
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
For each of the following find:
I. lim f (x) as x approaches a from the negative
II. lim f (x) as x approaches a from the positive
III. lim f (x) as x approaches a
a. f(x)={ sin x/3, if x< or equal to pi a=pi
{ x(root3)/(2pi), if x>pi
b. f(x)= (x^2-36)/root(x^2-12x+36) a=6
Answers
Answer:
a. For the function:
f(x) = { sin x/3, if x ≤ π
{ x√3/2π, if x > π
I. To find lim f(x) as x approaches π from the negative side, we need to evaluate f(x) for values of x that are slightly less than π. In this case, since sin(x/3) is a continuous function, we can simply evaluate it at x = π:
lim f(x) as x approaches π- = f(π-) = sin(π/3) = √3/2
II. To find lim f(x) as x approaches π from the positive side, we need to evaluate f(x) for values of x that are slightly greater than π. In this case, we can simply evaluate the other part of the piecewise function at x = π:
lim f(x) as x approaches π+ = f(π+) = π√3/2π = √3/2
III. To find lim f(x) as x approaches π, we need to check whether the left-hand and right-hand limits are equal. In this case, since both the left- and right-hand limits exist and are equal, we have:
lim f(x) as x approaches π = √3/2
b. For the function:
f(x) = (x^2 - 36)/√(x^2 - 12x + 36)
I. To find lim f(x) as x approaches 6 from the negative side, we need to evaluate f(x) for values of x that are slightly less than 6. In this case, we can substitute x = 6 - h, where h is a positive number approaching zero, to get:
lim f(x) as x approaches 6- = lim f(6 - h) as h approaches 0
Substituting x = 6 - h into the function, we get:
f(6 - h) = [(6 - h)^2 - 36]/√[(6 - h)^2 - 12(6 - h) + 36]
= [h^2 - 12h]/√[h^2]
Simplifying the numerator and denominator separately, we get:
f(6 - h) = h(h - 12)/|h|
Since h approaches 0 from the positive side, we have:
lim f(6 - h) as h approaches 0+ = lim h(h - 12)/h as h approaches 0+ = lim (h - 12) as h approaches 0+ = -12
II. To find lim f(x) as x approaches 6 from the positive side, we need to evaluate f(x) for values of x that are slightly greater than 6. In this case, we can substitute x = 6 + h, where h is a positive number approaching zero, to get:
lim f(x) as x approaches 6+ = lim f(6 + h) as h approaches 0
Substituting x = 6 + h into the function, we get:
f(6 + h) = [(6 + h)^2 - 36]/√[(6 + h)^2 - 12(6 + h) + 36]
= [h^2 + 12h]/√[h^2]
Simplifying the numerator and denominator separately, we get:
f(6 + h) = h(h + 12)/|h|
Since h approaches 0 from the positive side, we have:
lim f(6 + h) as h approaches 0+ = lim h(h +
Step-by-step explanation:
If ,f(x)=1/4x+3 what is the equation for f–1(x)?
f–1(x) = 4x - 3
f–1(x) = 4(x - 3)
f–1(x) = 4(x + 3)
f–1(x) = 4x + 3
Answers
Answer:
\(f {}^{ - 1} (x) = 4(x + 3)\)
Step-by-step explanation:
We would like to find the inverse of the following function .
\(\longrightarrow f(x) = \dfrac{1}{4}x +3 \)
Step 1 : Replace \(f(x) \) with \(y \) . We have
\(\longrightarrow y =\dfrac{1}{4}x +3 \)
Step 2 : Interchange x and y :-
\(\longrightarrow x = \dfrac{1}{4}y + 3 \)
Step 3 : Solve for y :-
\(\longrightarrow x - 3 =\dfrac{1}{4}y \)
Multiply both sides by 4,
\(\longrightarrow 4(x-3) = y \)
Step 4 : Replace y with f-¹(x) :-
\(\longrightarrow 4(x -3)=f^{-1}(x) \)
Interchange the sides ,
\(\longrightarrow \underline{\underline{ f^{-1}(x)= 4(x-3)}}{}\)
And we are done !
Express the given trigonometric functions in terms of the same function of a positive acute angle.sec 948 degrees, cos(-948) degrees
Answers
Given the Trigonometric Functions:
\(\begin{gathered} sec(948\text{\degree}) \\ \\ cos(-948\text{\degree}) \end{gathered}\)Using your calculator you get:
\(sec(948\text{\degree})\approx-1.49\)By definition, Secant is negative in Quadrant III.
Finds its Reference Angle as follows:
\(948\text{\degree}-5\cdot180\text{\degree}=48\text{\degree}\)Because:
\(\frac{948}{180}\approx5\)Then, you get:
\(=-sec\left(48\text{\degree}\right)\)Notice that:
\(cos(-948\text{\degree})\approx-0.67\)Then, you can conclude that it is in Quadrant II.
Therefore its Reference Angle is:
\(5\cdot180\text{\degree}-948\text{\degree}=-48\)So you can set up:
\(=-cos\lparen-48)\)By definition:
\(cos(-\theta)=cos\theta\)Therefore, you can rewrite it in this form:
\(=-cos(48\text{\degree})\)Hence, the answer is:
\(\begin{gathered} sec(48\text{\degree}) \\ \\ -cos(48\text{\degree}) \end{gathered}\)In AQRS, m
angle, then classify AQRS by its angles.
Classify:
m
m
m
Answers
Using Angle Sum property, the measure of 3 angles is ∠Q = 35°, ∠R = 19°, ∠S = 126°.
According to the triangle's "angle sum property," a triangle's angles add up to 180 degrees. Three sides and three angles, one at each vertex, make up a triangle. The sum of the interior angles in a triangle is always 180o, regardless of whether it is acute, obtuse, or right.
One of the most commonly applied properties in geometry is the triangle's angle sum property. Most often, the unknown angles are calculated using this attribute.
As given the measure of 3 angles is -
∠Q = 4x - 17
∠R = x + 6
∠S = 10x - 4
We know that by angle - sum property,
The sum of 3 angles of triangle = 180°
⇒ 4x - 17 + x + 6 + 10x - 4 = 180
⇒ 15x -15 = 180
⇒ 15x = 180 + 15
⇒ 15x = 195
⇒ x = 13
∠Q = 4x - 17 = 4 × 13 - 17 = 35°
∠R = x + 6 = 13 + 6 = 19°
∠S = 10x - 4 = 10 × 13 - 4 = 126°
To learn more about angle - sum property from given link
https://brainly.com/question/8492819
#SPJ1
Complete question -

A. Find the Mode, Median, Mean and Range. Show your work.
1. 24, 31, 12, 38, 13, 15, 46, 62.
2. 17, 66, 14, 79, 47, 95, 32, 21, 10, 58.
3. 53, 22, 76, 46, 68, 32, 15, 29.
4. 17, 24, 8, 19, 6, 34, 10, 28, 12.
5. 5, 8, 9, 10, 11, 15, 21, 32.
6. 28, 15, 15, 46, 27, 21, 24
B. Find the mode, median, and range
7) 5.2, 5.7, 5.2, 4.3, 3.6, 3.8, 2.7, 4.2, 4.3, 3.9, 4.2
8) 18.1 , 18.6, 18.2, 18.1, 18.9, 18.6, 18.7, 18.3, 18.2, 18.6, 18.6
C. Find the mode and median for each data.
9) 2/9 , 7/9, 5/9, 1/9, 3/9, 8/9
10) 1/4, 1/11, 1/6, 1/9, 1/3 , 1/10
Answers
A.
1. Mode: No mode. Median: 24. Mean: 30.875. Range: 50.
2. Mode: No mode. Median: 33.5. Mean: 43.9. Range: 85.
3. Mode: No mode. Median: 46. Mean: 43.571. Range: 61.
4. Mode: No mode. Median: 17. Mean: 18. Range: 28.
5. Mode: No mode. Median: 10.5. Mean: 13.5. Range: 27.
6. Mode: 15. Median: 22.5. Mean: 25.857. Range: 31.
B.
7. Mode: 4.3. Median: 4.2. Range: 2.1.
8. Mode: 18.6. Median: 18.6. Range: 0.8.
C.
9. Mode: No mode. Median: 4/9.
10. Mode: No mode. Median: 5/24.
Let i be the imaginary number √-1. Determine whether the expression a+bi, where a and b are real numbers, represents a real number or a non-real complex number for each case below. Select Real Number or Non-Real Complex number for each case.

Answers
Case 1: a = 0; b = 0 --> Real Number
Case 2: a = 0; b ≠ 0 --> Non-Real Complex Number
Case 3: a ≠ 0; b = 0 --> Real Number
Case 4: a ≠ 0; b ≠ 0 --> Non-Real Complex Number
Understanding Complex NumberFor each case, we can determine whether the expression a + bi represents a real number or a non-real complex number based on the values of a and b.
Case 1: a = 0; b = 0
In this case, both a and b are zero. The expression a + bi simplifies to 0 + 0i, which is equal to 0. Therefore, the expression represents a real number.
Case 2: a = 0; b ≠ 0
Here, a is zero, but b is nonzero. The expression a + bi becomes 0 + bi, where b is a nonzero real number multiplied by the imaginary unit i. Since the expression contains a nonzero imaginary part, it represents a non-real complex number.
Case 3: a ≠ 0; b = 0
In this case, a is nonzero, but b is zero. The expression a + bi simplifies to a + 0i, which is equal to a. As there is no imaginary part in the expression, it represents a real number.
Case 4: a ≠ 0; b ≠ 0
Here, both a and b are nonzero. The expression a + bi contains both a real part (a) and an imaginary part (bi). Thus, it represents a non-real complex number.
Learn more about complex number here:
https://brainly.com/question/5564133
#SPJ1

What is the value of x when h(x) = -3?
O-7
O-1
0 0
O2

Answers
7. A pupil sat for a test in five subjects.
He got a total of 380 marks. How
many marks did he lose if every
subject was marked out of 100?
A. 280 B. 500
C. 120
D 220
Answers
Answer:
option C: 120
Step-by-step explanation:
total marks = 5× 100 = 500
marks he obtained = 380
marks he lost = 500 - 380 = 120
plz mark my answer as brainlist plzzzz.
hope this will be helpful to you.
(1 point) A bucket that weighs 3.6 pounds and a rope of negligible weight are used to draw water from a well that is 78 feet deep. The bucket is filled with 38 pounds of water and is pulled up at a rate of 2.9 feet per second, but water leaks out of a hole in the bucket at a rate of 0.1 pounds per second. Find the work done pulling the bucket to the top of the well. Your answer must include the correct units. (You may enter lbf or lb*ft for ft-lb.)
Answers
Answer:
The total work done in pulling the bucket to the top of the well is approximately 3,139.1 ft·lb
Step-by-step explanation:
The given parameters are;
The mass of the bucket, W = 3.6 pounds
The depth of the well, h = 78 feet deep
The mass of water in the bucket = 38 ponds
The rate at which the water is pulled up = 2.9 feet per second
The rate at which water is leaking from the bucket, \(\dot m\) = 0.1 pounds per second
We separate and find the work done for lifting the bucket and the water individually, then we add the answers to get the solution to the question as follows;
The work done in lifting bucket empty from the well bottom, \(W_b\) = W × h
∴ \(W_b\) = 3.6 pounds × 78 feet = 280.8 ft-lb
The work done in lifting bucket empty from the well bottom, \(W_b\) = 280.8 ft-lb
The time it takes to lift the bucket from the well bottom to the top, 't', is given as follows;
Time, t = Distance/Velocity
The time it takes to pull the bucket from the well bottom is therefore;
t = 78 ft./(2.9 ft./s) ≈ 26.897
The time it takes to pull the bucket from the well bottom to the top, t ≈ 26.897 s
The mass of water that leaks out from the bucket before it gets to the top, m₂, is therefore;
m₂ = \(\dot m\) × t
∴ m₂ = 0.1 lbs/s × 26.897 s = 2.6897
The mass of the water that leaks, m₂ = 2.6897 lbs
The mass of water that gets to the surface m₃ = m - m₂
∴ m₃ = 38 lbs - 2.6897 lbs ≈ 35.3103 lbs
Given that the water leaks at a constant rate the equation representing the mass of the water as it is lifted can b represented by a straight line with slope, 'm' given as follows;
The slope of the linear equation m = (38 lbs - 35.3103 lbs)/(78 ft. - 0 ft.) = 0.03448\(\overline 3\) lbs/ft.
Therefore, the equation for the weight of the water 'w' can be expressed as follows;
w = 0.03448\(\overline 3\)·y + c
At the top of the well, y = 0 and w = 38
∴ 35.3103 = 0..03448\(\overline 3\) × 0 + c
c = 35.3103
∴ w = 0.03448\(\overline 3\)·y + 35.3103
The work done in lifting the water through a small distance, dy is given as follows;
(0.03448\(\overline 3\)·y + 38) × dy
The work done in lifting the water from the bottom to the top of the well, \(W_{water}\), is given as follows;
\(W_{water} = \int\limits^{78}_0 {0.03448\overline 3 \cdot y + 35.3103 } \, dy\)
\(\therefore W_{water} = \left [ {\dfrac{0.03448\overline 3 \cdot y^2}{2} + 35.3103 \cdot y\right ]^{78}_0\)
\(W_{water}\) = (0.034483/2 × 78^2 + 35.3103 × 78) - (0.034483 × 0 + 38 × 0) ≈ 2,859.1
The work done in lifting only the water, \(W_{water}\) ≈ 2,859.1 ft-lb
The total work done, in pulling the bucket to the top of the well, W = \(W_b\) + \(W_{water}\)
∴ W = 2,859.1 ft.·lb + 280.8 ft.·lb ≈ 3,139.1 ft·lb
The total work done, in pulling the bucket to the top of the well, W ≈ 3,139.1 ft·lb.
The mean is calculated for for 551 respondents and the result is 1.5
Answers
The level of measurement of the data can be given as follows:
Interval or ratio.
How to obtain the levels of measurement of the data?There are four levels of measurement for the data, given as follows:
Nominal.Ordinal.Interval.Ratios.The measures of central tendency for each level are given as follows:
Nominal: ModeOrdinal: Mode and median.Interval: Arithmetic mean, mode and median.Ratios: Arithmetic mean, geometric mean, mode and median.For this problem, we have the arithmetic mean, meaning that the level of measurement can be either interval or ratio.
Missing InformationThe problem asks for the level of measurement of the data.
More can be learned about level of measurement at https://brainly.com/question/17227965
#SPJ1
An equation is shown below:
4(x − 3) − 5(x + 1) = 3
Which statement shows a correct next step in solving the equation? (1 point)
A: The equation can become 4x − 12 − 5x − 5 = 3 by applying the associative property of multiplication.
B: The equation can become 4x − 3 − 5x + 1 = 3 by applying the associative property of multiplication.
C: The equation can become 4x − 3 − 5x + 1 = 3 by applying the distributive property.
D: The equation can become 4x − 12 − 5x − 5 = 3 by applying the distributive property.
Answers
your answer is a
and x equals 20