a parking garage charges $2.50 base free plus an hourly rate of $4.00. If you hve most $12.50 how many parking you can
Answers
Answer: 2.5 hours or 2 hr and 30 min
Step-by-step explanation:
We can set up an equation to find how many hours you can park.
2.5+4x=12.5
The 2.5 comes from the base fee. The 4x is the hourly rate, where x is hours. The 12.5 is the total amount of money you have.
Since we have our equation, we can solve for x.
4x=10
x=2.5
You can park for 2.5 hours, or 2 hours and 30 min.
Related Questions
Can someone help me?

Answers
Answer:
1 feet
Step-by-step explanation:
15-14
is it a b c or d ? please help i’m doing iready testing
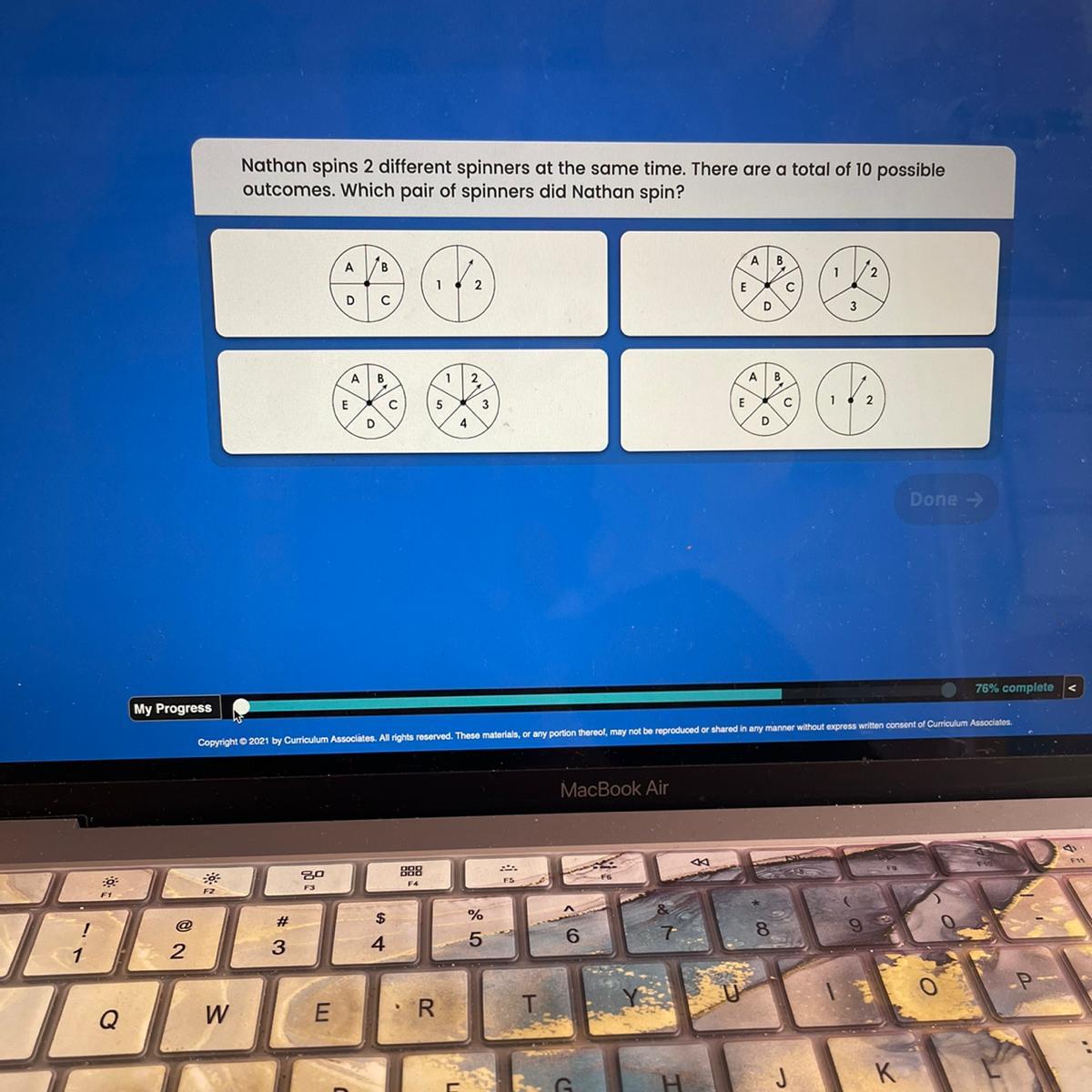
Answers
Answer:
the bottom left
Step-by-step explanation:
if it is right brainliest pls
Casey wants to determine what his classmates' favorite
summer break activities are. What percent of Casey's
classmates are boys who favor going to the beach in the
summer? Round your answer to the nearest percent.
Total
Playing
Sports
Going to
the Mall
Playing
Video
Games
22
8.
30
Going to
the
Beach
32
29
61
Boys
Girls
Total
10
12
22
17
16
33
81
65
146
32781
O
Ob
3296
Ос
39.596
Od
4096
Answers
Answer: what
Step-by-step explanation:
Speack english
Suppose you are given two sets A and B, each containing n positive integers. Youcan choose to reorder each set however you like. After reordering, leta, be the ith element in A, and by be the ith element in B. You will receive a payoff ofaba) If you reorder A and B into monotonically decreasing order, consider any indices i and j such that i < j, which of the two combinations has higher value: aibj +aibj or aibj + biaj? Prove your answer. Based on this, describe the optimal way of reordering that maximizes your payoff
Answers
The running time is O(n log(n)) since we sort two vector.
We solve the problem with the following algorithms:
1. Order A is in the increasing order.
2. Order B is in the decreasing order.
3. Return (A,B).
We must demonstrate that this is the best answer. without sacrificing generality, we can assume that a₁ ≤ a₂ ......≤ aₙ in the optimal solution.
Since the payoff is \(\prod_{i}^{n}=1^{a_{i}^{bi}}\), the payoff will always increase if we make a change so that \(b_{i+1} > b_{i}\).
Therefore the optimal solution will be found if B is sorted.
Thus, the running time is O(n log(n)) since we sort two vector.
Learn more about Algorithm here:
https://brainly.com/question/22984934
#SPJ4
If the sum of an infinite geometric series is \( \frac{15625}{24} \) and the common ratio is \( \frac{1}{25} \), determine the first term. Select one: a. 625 b. 3125 c. 25 d. 125
Answers
The first term of the infinite geometric series is 625.Let's dive deeper into the explanation.
We are given that the sum of the infinite geometric series is \(\( \frac{15625}{24} \)\)and the common ratio is\(\( \frac{1}{25} \).\)The formula for the sum of an infinite geometric series is \(\( S = \frac{a}{1 - r} \)\), where \( a \) is the first term and \( r \) is the common ratio.
Substituting the given values into the formula, we have \(\( \frac{15625}{24} = \frac{a}{1 - \frac{1}{25}} \).\)To find the value of \( a \), we need to isolate it on one side of the equation.
To do this, we can simplify the denominator on the right-hand side.\(\( 1 - \frac{1}{25} = \frac{25}{25} - \frac{1}{25} = \frac{24}{25} \).\)
Now, we have \(\( \frac{15625}{24} = \frac{a}{\frac{24}{25}} \).\) To divide by a fraction, we multiply by its reciprocal. So, we can rewrite the equation as \( \frac{15625}{24} \times\(\frac{25}{24} = a \).\)
Simplifying the right-hand side of the equation, we get \(\( \frac{625}{1} = a \).\)Therefore, the first term of the infinite geometric series is 625.
In conclusion, the first term of the given infinite geometric series is 625, which corresponds to option (a).
learn more about geometric series here here
https://brainly.com/question/30264021
#SPJ11
What is the greatest common factor of 9 and 54? The GCF of 9 and 54 is
Answers
Answer:
9
hope this helps :)
9 Hope you find it helpful :)
According to a certain country's department of education, 40.4% of 3 -year-olds are enrolled in day care. What is the probabily that a randomily selecind 3-year-old is enrolled in day care? The probability that a randomly selected 3-year-old is enrolled in day care is (Type an integer or a decimal.)
Answers
The probability that a randomly selected 3-year-old is enrolled in daycare is 0.404 or 40.4%.
According to the information provided, 40.4% of 3-year-olds are enrolled in daycare. This means that out of all the 3-year-olds in the population, 40.4% of them attend daycare. Therefore, the probability of randomly selecting a 3-year-old who is enrolled in daycare is 0.404 or 40.4%.
Probability is a measure of the likelihood of an event occurring. In this case, the event is a randomly selected 3-year-old being enrolled in daycare. The probability is calculated by dividing the number of favorable outcomes (3-year-olds enrolled in daycare) by the total number of possible outcomes (all 3-year-olds). Since the given information states that 40.4% of 3-year-olds are enrolled in daycare, we can directly interpret it as the probability of selecting a randomly chosen 3-year-old who is enrolled in daycare. Therefore, the probability is 0.404 or 40.4%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
I really need help ONLY QUESTION 3

Answers
They drew 3 and each got 1 point so 3 x 1 = 3 points
They lost 3 matches and each got -2 so 3 x -2 = -6
Altogether they got 72 points as 75+3-6=72
However they started on -14 so 72-14 equals 58 therefore at the end of the season they had 58 points
Hope this helps !
In contrast to mass media, interactive media messages converge, which mean that they _____. Group of answer choices can be sent one to one, one to many, or many to many are only sent from one to many are a one-to-one interaction are not sent and received in real time
Answers
In contrast to mass media, interactive media messages converge, which means that they can be sent one to one, one to many, or many to many. The statement is true. Interactive media refers to media that allows active participation from the user, rather than one-way communication.
Interactive media messages converge, which means that they can be sent one to one, one to many, or many to many. This refers to the flexibility that is available for interactive media messages compared to mass media.In the case of interactive media, feedback is not only encouraged but also acknowledged and included in the ongoing communication process. In addition, as opposed to mass media, interactive media allows for one-on-one conversations between participants as well as between a sender and many recipients. The sender is not the only one conveying the message. The recipients can also send messages back, resulting in a more interactive experience.
Know more about one-way communication here:
https://brainly.com/question/32631876
#SPJ11
Find two numbers whose sum is 45 and whose difference is 19.
Answers
Answer: 32 and 13
Step-by-step explanation:
32+13=45
32-13=19
Answer:
32 and 13
Step-by-step explanation:
Mrs. Huber opened a savings account on june 26 with a $1,300 deposit. The account pays 1.6% interest compounded daily.
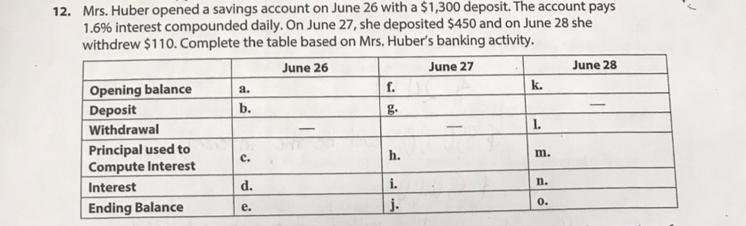
Answers
In table the missing entity are :
1. On June 26, the values are a is 0 , b is $ 1300 , c is $1300 , d is $20.8 and e is $ 1320.8
2. On June 27, the values are f is $ 1320.8 , g is 0 , h is $ 1300 , I is $ 41.93 and j is $ 1341.93
3. On June 28, the values are k is $ 1341.93 , l is 0 , m is $ 1300 , n is $ 63.40 and o is $ 1363.40.
What is compound interest ?
The interest on savings that is calculated using both the original principal and the interest accrued over time is called compound interest.
It is given that , the initial deposit is of $1300 on date 26th of June.
The rate of compound interest = 1.6%
We know that the formula to find out the compound interest on a deposit is given by:
CI = P × \([1 + \frac{r}{100}]^{t}\)
Here : P is the principal amount and r is the rate of interest in %.
On June 26 :
Opening balance = 0
Deposit = $ 1300
Principal used = $ 1300
Compound interest will be :
CI = 1300 × \([1 + \frac{1.6}{100}]^{1}\)
CI = $ 1320.8
This is the ending balance.
Interest = 1320.8 - 1300 = $ 20.8
On June 27 :
Opening balance = $ 1320.8
Deposit = 0
Principal used = $ 1300
CI = 1300 × \([1 + \frac{1.6}{100}]^{2}\)
CI = $ 1341.93
This is the ending balance.
Interest = 1341.93- 1300 = $ 41.93
On June 28 :
Opening balance = $ 1341.93
Deposit = 0
Principal used = $ 1300
CI = 1300 × \([1 + \frac{1.6}{100}]^{3}\)
CI = $ 1363.40
This is the ending balance.
Interest = 1363.40 - 1300 = $ 63.40
Therefore , in table the missing entity are :
1. On June 26, the values are a is 0 , b is $ 1300 , c is $1300 , d is $20.8 and e is $ 1320.8
2. On June 27, the values are f is $ 1320.8 , g is 0 , h is $ 1300 , I is $ 41.93 and j is $ 1341.93
3. On June 28, the values are k is $ 1341.93 , l is 0 , m is $ 1300 , n is $ 63.40 and o is $ 1363.40.
Learn more about compound interest here :
https://brainly.com/question/24924853
#SPJ1
There are 5 positions available in the new school. Of the applicant, 12 are men and 8 are women. In how many ways can 3 men and 2 women be chosen if they are equally considered?
Answers
There are 3080 ways 3 men and 2 women can be chosen if they are equally considered, using the multiplication principle of counting
What is the multiplication principle of countingThe multiplication principle states that if there are m ways to perform one task and n ways to perform another task, then there are m x n ways to perform both tasks together.
To find the number of ways to choose 3 men from the 12 men, we can use the formula for combination, which is: ⁿCᵣ = n! / (r! (n-r)!).
where n is the total number of men and r is the number of men chosen
so, the number of ways to choose 3 men from the 12 men = ¹²C₃ = 1.
Similarly, we evaluate the number of ways to choose 2 women from the 8 women
as = ⁸C₂ = 14
Now, using the multiplication principle, we can find the total number of ways 3 men and 2 women be chosen if they are equally considered.
220 x 14 = 3080
Therefore, there are 3080 ways 3 men and 2 women can be chosen if they are equally considered, using the multiplication principle of counting
Know more about multiplication principle here:https://brainly.com/question/10275154
#SPJ1
Raul is moving from Houston, Texas to Los Angeles, California for his new job. In Houston, he makes $70,000 per year but does not have to pay state income tax. His new job in L.A. pays $110,000 per year but he has to pay a 10% state tax on his salary. By what percent does his salary actually increase? Round your answer to the nearest tenth of a percent (one decimal place).
Answers
Given:
Raul's salary
Houston $ 70,000
Los Angeles $ 110,000 ( w 10% state tax)
Requird: actual % salary increase
Solution
Cost of the state tax = 10% ( $110,000) = (0.10) (110000) = $ 11, 000
The state tax will be deducted from his salary in Los Angeles, leaving him with only
$ 110,000 - $11, 000 = $ 99,000
Actual increase in salary = $ 99,000 - $ 70,000 = $ 29,000
% salary increase = ( actual salary increase/ salary in houston)*100 = ( $ 29,000 / $ 70, 000 )*100= 41.4%
Suppose that Y and X have a joint normal distribution with mean (μ y
,μ x
) T
and covariance matrix Σ yx
=( σ y
2
σ yx
σ yx
σ x
2
). (a) Find the conditional expectation E[Y∣X=x] (b) Find the conditional variance Var(Y∣X=x) (c) Write the expression for the conditional pdf for Y given X=x
Answers
The conditional expectation E[Y|X=x] is calculated by adjusting the mean of Y based on the specific value of X, the conditional variance Var(Y|X=x) is obtained by subtracting the contribution of X from the overall variance of Y.
(a) The conditional expectation E[Y|X=x] is the expected value of Y given a specific value of X, which can be calculated using the formula E[Y|X=x] = μy + (σyx/σx^2)(x - μx).
(b) The conditional variance Var(Y|X=x) is the variance of Y given a specific value of X, and it can be calculated using the formula Var(Y|X=x) = σy^2 - (σyx^2/σx^2).
(c) The conditional pdf for Y given X=x can be written using the joint normal distribution properties. Assuming Y and X are jointly normally distributed, the conditional distribution of Y given X=x is also normally distributed. The conditional pdf can be expressed as f(Y|X=x) = (1/√(2πVar(Y|X=x))) * exp(-(Y - E[Y|X=x])^2 / (2Var(Y|X=x))).
Learn more about conditional variance here:
https://brainly.com/question/15071440
#SPJ11
y= 4x^2-8x+9
find the vertex, domain, and range.
Answers
Answer:
Vertex: (4,41)
Step-by-step explanation:
You have to use the formula ax^2 + bx + c. Then you have to do a = 4 b = -8 c = 9. Then input the values to the equation -b/2a . I feel like this is how. Im not sure how to find the domain and range though i forgot sorry
Plsss help meee. Worth 15 points<3
A sentence with antonyms has two words with
somewhat different meanings
opposite meanings
similar meanings
the same meanings
Answers
Answer:
a word opposite in meaning to another (ex bad and good)
Complete the explanation of the subtraction using the adding distances strategy.
29-18
29-18
is the ten-multiple between 29 and 18.
The distance from 18 to 20 is
The distance from 20 to 29 is
29 - 18 =
= 11
Answers
The difference between 29 and 18 is 11.
To subtract 18 from 29 using the adding distances strategy, we first identify the ten-multiple between the two numbers, which is 20.
To find the distance from 18 to 20, we subtract 18 from 20, resulting in a distance of 2. This means we need to add 2 to 18 to reach 20.
Next, we determine the distance from 20 to 29 by subtracting 20 from 29, which gives us a distance of 9. So, we need to add 9 to 20 to reach 29.
To find the difference between 29 and 18, we add the distances obtained from the two steps. Adding 2 to 18 gives us 20, and adding 9 to 20 gives us 29. Therefore, the answer is 11, which represents the difference between 29 and 18.
Using the adding distances strategy, we break down the subtraction problem into smaller steps by considering the distances between relevant ten-multiples.
By adding these distances together, we can determine the final difference between the two numbers.
For more such questions on difference
https://brainly.com/question/148825
#SPJ8
37.67 x 70.71 (please show the work) but I need u to explain with numbers
Answers
x
70.71
————
2663.6457

(10 points) find tan if is the distance from the point (1,0) to the point (0.75,0.66) along the circumference of the unit circle.
Answers
The value of tan(θ) is approximately 0.88.
To find the value of tan(θ) when the distance from the point (1,0) to the point (0.75, 0.66) along the circumference of the unit circle, we'll first find the angle θ using the given points.
1. Since we're given points on the unit circle, we know their coordinates represent the cosine and sine values, i.e., (cos(θ), sin(θ)) = (0.75, 0.66).
2. Now, we need to find the value of tan(θ), which can be calculated using the formula: tan(θ) = sin(θ) / cos(θ).
3. Plugging in the values we have: tan(θ) = 0.66 / 0.75.
4. Performing the calculation, we get: tan(θ) ≈ 0.88.
5. Therefore, the value of tan(θ) when the distance from the point (1,0) to the point (0.75, 0.66) along the circumference of the unit circle is approximately 0.88.
To know more about circumference click on below link:
https://brainly.com/question/4268218#
#SPJ11
I seriously need help on this question, can someone help?

Answers
Answer:
a. A + C < B + C
Step-by-step explanation:
when we know that A < B, then adding the same amount to both sides did not change the relationship between both sides.
this is like having a balance with 2 cups. one side is heavier than the other, so the heavier cup is down.
if we add the same weight to both cups, the situation will not change.
that is why a. is the right answer.
b. would only be right, if C is negative.
for positive C the same argument as for A applies. a smaller amount (or weight) stays smaller also after multiplying both sides by the same number.
but because this option would only be right for a subset of the possible values, this is not true in general.
c.
this is not true at all.
if we multiply the expression by -1, then the inequality sign has to flip. < becomes >, > becomes <.
which did not happen here.
A group of 75 math students were asked whether they
like algebra and whether they like geometry. A total of
45 students like algebra, 53 like geometry, and 6 do
not like either subject.
Algebra vs. Geometry
Likes Algebra
Does Not
Like Algebra
Total
Likes
Geometry
Mark this and return
a
3
53
Does Not
Like Geometry
b
6
e
Total
45
P
75
What are the correct values of a, b, c, d, and e?
a 16, b = 29, c = 22, d = 30, e = 24
a = 29, b = 16, c = 30, d = 22, e = 24
a 16, b = 29, c = 24, d = 22, e = 30
H
a = 29, b = 16, c = 24, d = 30, e = 22
Answers
The correct values for a, b, c, d, and e are a = 16, b = 29, c = 24, d = 22, and e = 30 for group of 75 students on asking whether they like Algebra or Geometry.
For the values of a, b, c, d, and e, we can use the information provided in the table. Let's break it down step-by-step:
We are given that a total of 75 math students were surveyed. Therefore, the total number of students should be equal to the sum of the students who like algebra, the students who like geometry, and the students who do not like either subject.
75 = 45 (Likes Algebra) + 53 (Likes Geometry) + 6 (Does Not Like Either)
Simplifying this equation, we have:
75 = 98 + 6
75 = 104
This equation is incorrect, so we can eliminate options c and d.
Now, let's look at the information given for the students who do not like geometry. We know that a + b = 6, where a represents the number of students who like algebra and do not like geometry, and b represents the number of students who do not like algebra and do not like geometry.
Using the correct values for a and b, we have:
16 + b = 6
b = 6 - 16
b = -10
Since we can't have a negative value for the number of students, option a is also incorrect.
The remaining option is option e, where a = 29, b = 16, c = 24, d = 22, and e = 30. Let's verify if these values satisfy all the given conditions.
Likes Algebra: a + c = 29 + 24 = 53 (Matches the given value)
Does Not Like Algebra: b + d = 16 + 22 = 38 (Matches the given value)
Likes Geometry: c + d = 24 + 22 = 46 (Matches the given value)
Does Not Like Geometry: b + e = 16 + 30 = 46 (Matches the given value)
All the values satisfy the given conditions, confirming that option e (a = 29, b = 16, c = 24, d = 22, and e = 30) is the correct answer.
For more such information on Algebra and Geometry:
https://brainly.com/question/24696219
#SPJ8
In a survey given by camp counselors, campers were
asked if they like to swim and if they like to have a
cookout. The Venn diagram displays the campers'
preferences.
Camp Preferences
S
0.06
0.89
C
0.04
0.01
A camper is selected at random. Let S be the event that
the camper likes to swim and let C be the event that the
camper likes to have a cookout. What is the probability
that a randomly selected camper does not like to have a
cookout?
O 0.01
O 0.04
O 0.06
O 0.07
Answers
The probability is 0.96 that a randomly selected camper does not like to have a cookout, based on the given information and the complement rule of probability.
To determine the probability that a randomly selected camper does not like to have a cookout, we need to find the complement of the event C (the event that the camper likes to have a cookout).
Looking at the Venn diagram, we see that the probability of event C is 0.04 (represented by the intersection of circles C and A). Therefore, the probability of the complement of event C (not liking to have a cookout) is equal to 1 minus the probability of event C.
1 - 0.04 = 0.96
Hence, the probability that a randomly selected camper does not like to have a cookout is 0.96.
For more such questions on probability
https://brainly.com/question/24756209
#SPJ8
Plssssss!!!! Help SOLVE FOR Y!!!!!!

Answers
Answer:
y = 23 degrees
Step-by-step explanation:
115° and 5y° are equal because they are alternate exterior angles
115 = 5y
Divide by 5 to isolate the y
23 = y
so y is 23°
Mary, Katherine, and Alex share the bill at a restaurant after a meal. Mary pays for of the bill, Katherine pays for of the bill, and Alex
pays for the rest. What is the ratio of Mary's share to Katherine's share to Alex's share?
Answers
The ratio of Mary's share to Katherine's share to Alex's share is 5:4:1, which means Mary pays 5/10 of the bill, Katherine pays 4/10 of the bill, and Alex pays 1/10 of the bill.
To find the ratio, we can write their contribution as a fraction of the total parts and then solve the fractions then they'll have the same denominator.
So, Mary's share is 5/10, Katherine's share is 4/10, and Alex's share is 1/10.
To convert this as a ratio, we write 5:4:1, where each number represents the number of parts each person pays, and the colon separates each person's contribution.
Therefore, the ratio of Mary's share to Katherine's share to Alex's share is 5:4:1
To learn more about ratios:
https://brainly.com/question/12024093
#SPJ4
use the definition to find an expression for the area under the graph of f as a limit. do not evaluate the limit. f(x) = x2 + 1 + 2x , 7 ≤ x ≤ 9
Answers
An expression for the area under the graph of f as a limit. A = ∫[7, 9] f(x) dx = lim (n→∞) Σ [f(7 + i(2/n))(2/n)]
To find an expression for the area under the graph of f(x) = x^2 + 1 + 2x, 7 ≤ x ≤ 9, as a limit, we can use the definition of the definite integral.
The definite integral of a function f(x) over the interval [a, b] is given by the limit of a sum as the partition gets finer. In this case, we can approximate the area under the graph by dividing the interval [7, 9] into smaller subintervals.
Let's choose n subintervals and denote Δx as the width of each subinterval. In this case, Δx = (9 - 7)/n = 2/n. We can choose any representative point xi* in each subinterval, and in this case, let's choose xi* as the right endpoint of each subinterval.
Now, the area of each subinterval can be approximated by the height of the function at the right endpoint multiplied by the width of the subinterval:
ΔAi ≈ f(xi*)Δx = f(7 + i(2/n))(2/n)
The total area under the graph is then approximated by the sum of all the subinterval areas:
A ≈ Σ ΔAi ≈ Σ [f(7 + i(2/n))(2/n)]
As we take the limit as n approaches infinity, the partition gets finer, and the approximation becomes more accurate. Therefore, the expression for the area under the graph of f(x) as a limit is:
A = ∫[7, 9] f(x) dx = lim (n→∞) Σ [f(7 + i(2/n))(2/n)]
Note that this is the expression for the definite integral of f(x) over the interval [7, 9], and evaluating the limit will give the exact value of the area under the graph.
To know more about limit refer here:
https://brainly.com/question/12383180#
#SPJ11
11)Find the magnitude and direction of the resultant of the vectors
u and v and prove by sketching all three vectors.
u = 600 CiS 120°
v = 70 CiS 45°
Answers
the magnitude of the resultant vector R is approximately 622.99, and its direction is approximately -67.6°.
The magnitude and direction of the resultant vector of u and v can be found by adding the two vectors using the parallelogram method. First, we convert the vectors from polar form to rectangular form.
1. Convert u from polar form to rectangular form:
u = 600 CiS 120°
The magnitude of u is 600 and the angle is 120°. To convert to rectangular form, we use the following equations:
x = magnitude * cos(angle)
y = magnitude * sin(angle)
Calculating x:
x = 600 * cos(120°)
x = -300
Calculating y:
y = 600 * sin(120°)
y = 519.62
Therefore, u in rectangular form is u = (-300, 519.62).
2. Convert v from polar form to rectangular form:
v = 70 CiS 45°
The magnitude of v is 70 and the angle is 45°. Using the same equations as above, we get:
x = 70 * cos(45°)
x = 49.5
y = 70 * sin(45°)
y = 49.5
Therefore, v in rectangular form is v = (49.5, 49.5).
3. Add the rectangular vectors u and v:
Resultant vector, R = u + v
R = (-300, 519.62) + (49.5, 49.5)
R = (-250.5, 569.12)
4. Find the magnitude of the resultant vector R:
Magnitude of R = sqrt((\(-250.5)^2\) + \((569.12)^2)\)
Magnitude of R ≈ 622.99
5. Find the direction of the resultant vector R:
Direction of R = arctan(y/x)
Direction of R = arctan(569.12/-250.5)
Direction of R ≈ -67.6°
6. Sketch the vectors u, v, and R:
Draw a coordinate system and plot the vectors u and v according to their rectangular forms. Starting from the origin, draw a vector from the origin to the point (-300, 519.62) for u and from the origin to the point (49.5, 49.5) for v. Finally, draw the resultant vector R from the origin to the point (-250.5, 569.12).
By following these steps, we find that the resulting vector R has a magnitude of roughly 622.99 and a direction of approximately -67.6°.
For more such questions on magnitude, click on:
https://brainly.com/question/30337362
#SPJ8
There are 44,000 adults living in Oak city in examining attitudes according to the news of research group as random sample of Oak city adults what is your main source of news the results are shown below based on the sample predict the number of adults in Oak city whose main source of the news is television on your answer to the nearest whole number do not run by any intermittent calculations
Answers
The predicted number of adults in Oak City whose main source of news is newspapers or the radio is 85
To predict the number of adults in Oak City whose main source of news is newspapers or the radio, we need to add the number of adults who answered "Newspapers" to the number of adults who answered "Radio".
According to the sample data
Number of adults who answered "Newspapers": 64
Number of adults who answered "Radio": 21
Therefore, the predicted number of adults in Oak City whose main source of news is newspapers or the radio we have to use the addition
64 + 21 = 85
Rounding this answer to the nearest whole number, we get
85 ≈ 85
Learn more about addition here
brainly.com/question/29791798
#SPJ4
The given question is incomplete, the complete question is:
There are 44,000 adults living in Oak City. In examining attitudes toward the news, a research group asked a random sample of Oak City adults "What is your main source of news?" The results are shown below. Main Source of News Newspapers Number of Adults 64 Internet 80 Television 126 Radio 21 Other 40 Based on the sample, predict the number of adults in Oak City whose main source of news is newspapers or the radio. Round your answer to the nearest whole number.
a fair die is rolled times. what is the probability of having no and no among the rolls? round your answer to three decimal places.
Answers
The probability of rolling no 2's and no 5's in 10 rolls is approximately 0.107.
The probability of rolling no 2's and no 5's on a fair die can be calculated using the formula for the probability of independent events:
P(A and B) = P(A) x P(B)
where P(A) is the probability of event A occurring, and P(B) is the probability of event B occurring.
The probability of rolling any number other than 2 or 5 on a single roll of a fair die is 4/6, or 2/3. Since each roll is independent, the probability of rolling no 2's and no 5's in n rolls can be calculated as follows:
P(no 2's and no 5's in n rolls) = (4/6)^n
To round the answer to three decimal places, we can use a calculator. For example, if n = 10, the probability is:
P(no 2's and no 5's in 10 rolls) = \((4/6)^10\) = 0.107
So the probability of rolling no 2's and no 5's in 10 rolls is approximately 0.107, rounded to three decimal places.
Learn more about probability at
brainly.com/question/17089724
#SPJ4
Need Help fast, with steps

Answers
Answer:The solution is in the attached file below
Step-by-step explanation:

Please answer asapWhat is the measure of an exterior angle of a regular 13-sided polygon? Enter your answer as a decimal in the box. Round to the nearest tenth of a degree.
Answers
Answer:
Step-by-step explanation:
it is given by the formula=4× 90/ n
where n = number of sides
exterior angle= 4 x 90/13
=360/13=\(27.7\)°