A parliament has seats for 2 parties, party A has 60 members and party B has 80. While voting on resolution R, 60% of party A votes against the resolution while only 25% of party B votes against the resolution. If we were to randomly select 40 members from the parliament, what is the probability of:
1. At least 25/40 members vote against the resolution
2. At least 25/40 members vote for the resolution
Answers
1. The probability of at least 25/40 members voting against the resolution is 0.92114
2. the probability of at least 25/40 members voting for the resolution is 0.92114.
We are to find the probability of the following events:
First, we find the number of members who are likely to vote against the resolution from each party.
Number of members from Party A who would vote against the resolution = 60% of 60 = 0.60 × 60 = 36.
Number of members from Party B who would vote against the resolution = 25% of 80 = 0.25 × 80 = 20.
Thus, the total number of members who would vote against the resolution = 36 + 20 = 56.
Number of members who would vote in favor of the resolution = Total members − Number of members who would vote against the resolution= 60 + 80 − 56 = 84.
Let X be the number of members voting against the resolution. If X follows a binomial distribution with n = 40 and p = 56/140 = 0.4, we can find the probability of the events as follows:
1. The probability of at least 25/40 members voting against the resolution:
P(X ≥ 25) = 1 − P(X < 25)
We can use the binomial distribution table to find the probabilities associated with different values of X.
P(X < 25) = P(X = 0) + P(X = 1) + ... + P(X = 24)
Using the binomial distribution formula, we get:
P(X = k) = (nCk) × pk × (1 − p)n−k, where nCk is the number of ways of choosing k members out of n.
Using the formula, we can calculate the probabilities of P(X < 25) and P(X ≥ 25) as follows:
P(X < 25) = 0.000236 + 0.003226 + 0.020408 + 0.076306 + 0.182424 + 0.291878 + 0.338993 + 0.245031= 0.078858P(X ≥ 25) = 1 − P(X < 25)= 1 − 0.078858= 0.92114
Thus, the probability of at least 25/40 members voting against the resolution is 0.92114
2.The probability of at least 25/40 members voting for the resolution:
P(X ≥ 25) = 1 − P(X < 25)
We can use the binomial distribution table to find the probabilities associated with different values of X.P(X < 25) = P(X = 0) + P(X = 1) + ... + P(X = 24)
Using the binomial distribution formula, we get:
P(X = k) = (nCk) × pk × (1 − p)n−k, where nCk is the number of ways of choosing k members out of n.
Using the formula, we can calculate the probabilities of P(X < 25) and P(X ≥ 25) as follows:
P(X < 25) = 0.000236 + 0.003226 + 0.020408 + 0.076306 + 0.182424 + 0.291878 + 0.338993 + 0.245031= 0.078858
P(X ≥ 25) = 1 − P(X < 25)= 1 − 0.078858= 0.92114
Thus, the probability of at least 25/40 members voting for the resolution is 0.92114.
To know more about probability, visit the link : https://brainly.com/question/13604758
#SPJ11
Related Questions
is Average velocity equation rearranged to find the area under the curve?
Answers
Yes, the equation of velocity is rearranged to find the area under the curve.
The equation of velocity in general is v = d/t
where v = velocity, d = distance, and t = time.
We rearrange this equation to create an equation for distance and the equation of distance determines the area under the curve.
Our motive is to isolate the variable whose equation we want to create. So, in this case, isolate 'd' and move all other variables to the other side.
1. Multiply both sides by t
v × t = d/t × t
2. Cancel the t where appropriate
v × t = d
3. We get the equation for d
d = v × t
Now, this equation is used to find the area under the curve.
To learn more about average velocity;
https://brainly.com/question/1844960
#SPJ4
what does x equal?? T—T

Answers
Answer:
x= 20
Step-by-step explanation:
simplify by using cross multiplication
60=3x
now transpose the 3
60/3= x
20= x
if you have any questions pls list them in the comments.
Answer:
x=20
Step-by-step explanation:
5/3 and x/12 are proportional to each other so how 3 is proportional to 12 is how 5 is proportional to x. 12/3=4 so the common thing is 4. Now we multiply 5 by 4 which makes x=20.
I hope this helps :)
Consider the LP below. The BFS ("corners") are (0,0) (0,4) (1,4) (3,2) (3,0). The optimal solution is at x_{1} = 3 and x_{2} = 2
max z = 2x_{1} + x_{2}
s.t.
matrix x 1 +x 2 &<= 0 \\ x 1 &<=3\\ x 2 &<4 matrix
x_{1}, x_{2} >= 0
(a). What is the range of c_{1} the objective coefficient of x_{1} (currently 2) for which this BFS remains optimal:
(b). What is the range of b_{2} the right hand side of the second constraint (currently 3) for which this BFS remains optimal:
(c). What is the dual price of the second constraint?
Answers
(a) The range of c₁ (the objective coefficient of x₁) for which this BFS remains optimal is c₁ ≤ 2.
(b) The range of b₂ (the right-hand side of the second constraint) for which this BFS remains optimal is 3 ≤ b₂ < 4.
(c) The dual price of the second constraint is 0.
(a) The optimality condition for a linear programming problem requires that the objective coefficient of a non-basic variable (here, x₁) should not increase beyond the dual price of the corresponding constraint. In this case, the dual price of the second constraint is 0, indicating that increasing the coefficient of x₁ will not affect the optimality of the basic feasible solution. Therefore, the range of c₁ for which the BFS remains optimal is c₁ ≤ 2.
(b) The range of b₂ for which the BFS remains optimal is determined by the allowable range of the corresponding dual variable. In this case, the dual price of the second constraint is 0, implying that the dual variable associated with that constraint can vary within any range. As long as 3 ≤ b₂ < 4, the dual variable remains within its allowable range, and thus, the BFS remains optimal.
(c) The dual price of a constraint represents the rate of change in the objective function value per unit change in the right-hand side of the constraint, while keeping all other variables fixed. In this case, the dual price of the second constraint is 0, indicating that the objective function value does not change with variations in the right-hand side of that constraint.
Learn more about coefficient
brainly.com/question/1594145
#SPJ11
5th grade math. Decimals. Correct answer will be marked brainliest.

Answers
Answer:
4.71 +3.80 =8.51
Step-by-step explanation:
Answer:
8.51
Step-by-step explanation:
4.71
+ 3.80
------------
8.51
~Ren
Find a vector orthogonal to (8,0,3) and (−6,1,3). Choose the correct answer below. A. (3,42,8) B. (−3,42,8) C. (−3,−42,8) D. (−3,−42,−8)
Answers
The vector orthogonal to (8, 0, 3) and (-6, 1, 3) is (-3, -42, 8). The dot product of (a, b, c) and (8, 0, 3) must be zero. Similarly, for (a, b, c) to be orthogonal to (-6, 1, 3), the dot product of (a, b, c) and (-6, 1, 3) must be zero. Solving equations (1) and (2), we get a = -3, b = -42, and c = 8.
The solution of the given problem is:
Let the vector orthogonal to (8, 0, 3) and (-6, 1, 3) be (a, b, c).For (a, b, c) to be orthogonal to (8, 0, 3), the dot product of (a, b, c) and (8, 0, 3) must be zero.
Similarly, for (a, b, c) to be orthogonal to (-6, 1, 3), the dot product of (a, b, c) and (-6, 1, 3) must be zero.Dot product of (a, b, c) and (8, 0, 3) is:8a + 0b + 3c = 0 ...(1)
Dot product of (a, b, c) and (-6, 1, 3) is:-6a + b + 3c = 0 ...(2)
Solving equations (1) and (2), we geta = -3, b = -42, and c = 8
Therefore, the vector orthogonal to (8, 0, 3) and (-6, 1, 3) is (-3, -42, 8).Thus, the correct option is (D) (-3, −42, −8).
To know more about orthogonal visit:-
https://brainly.com/question/32196772
#SPJ11
Vertex: (5,4) Point: (2,1)
Answers
Lea
owhs 800 shares of ABC, Incorporated. On April 6, the corporation Instituted a 5-for-2 stock split. Before the split, each share was worth $42.60.
a. How many shares did Lea hold after the split?
b. What was the post-split price per share?
c. Show that the split was a monetary non-event for Lea. Pre-split and post-split market values=
Answers
Answer:
2000
Step-by-step explanation:
Number of shares after split is 5/2 times the pre split value =800*5/2 = 2000
A linear function contains the following points.
What are the slope and y-intercept of this function?
A. The slope is -3.
The y-intercept is (0, -7).
B. The slope is 1/3
The y intercept (0,-7)
c. The slope is -1/3
The y intercept s (0, -7).
D. The slope is -1/3
The y intercept is (-7,0)

Answers
Answer:
C
Step-by-step explanation:
The index of refraction of the core of a typical fiber optic is ncore = 1.46; the cladding has nclad = 1.4. calculate the critical angles for the total internal reflection icrit and crit .
Answers
Critical angle for the total internal reflection icrit, β = 78.28⁰
Critical angle for the total internal reflection crit, α = 17,22⁰
We have the refractive index of core, \(n_c_o_r_e\) = 1.46
We have the refractive index of clad , \(n_c_l_a_d\) = 1.4
Critical angle can be defined as the incidence angle which results in the refraction angle being equal to at that angle of incidence.
For Total Internal Reflection to occur, the incidence angle must be greater than the critical angle.
We know that the critical angle, θ is given by:
sinθ = \(\frac{n_c_l_a_d}{n_c_o_r_e}\)
sinθ = \(\frac{1.4}{1.46}\)
sinθ = 0.959 = sin⁻¹(0.979) = 78.28⁰
β = θ = 78.28⁰
Now, for α:
\(\frac{sin(90-\alpha )}{sin\alpha } = \frac{1}{n_c_o_r_e}\)
sinα = sin(90⁰-78.28⁰) × 1.46
sinα = sin(11.72⁰) × 1.46
α = sin⁻¹(0.296)
α = 17,22⁰
For more information on this visit:
https://brainly.com/question/13193665
#SPJ4
Critical angle for total internal reflection icrit β = 78.28⁰
Critical angle for total internal reflection crit, α = 17.22⁰
The critical angle can be defined as the angle of incidence at which the angles of refraction are equal to angle of incidence.
The angle of incidence must be greater than the critical angle for total internal reflection to occur.
The refractive index of the core is ncore = 1.46.
The refractive index of clad is nclad = 1.4.
We know that the critical angle, θ is given by:
sinθ = nclad/ ncore
sinθ = 1.4/1.46
sinθ = 0.959
sin⁻¹(0.979) = 78.28⁰
β = θ = 78.28⁰
Now, for α:
sin(90- α) / sin α = 1 / ncore
sinα = sin(90⁰-78.28⁰) × 1.46
sinα = sin(11.72⁰) × 1.46
α = sin⁻¹(0.296)
α = 17.22⁰
Critical angle for icrit β = 78.28⁰
Critical angle for crit α = 17.22⁰
Learn more about Total internal reflection here
https://brainly.com/question/13088998
#SPJ4
What is the value of x?

Answers
Answer:
x = 20°
I hope it helps!
Step-by-step explanation:
80+a=180
a=100
a=2x+3x
100=5x
x=20

Sara deposited $150 to open a new bank account before she paid $225 for her portion of the rent. Her bank charged her a $50 overdraft fee. Then she deposited her paycheck of $450. How much money is in Sara’s account now? *
Answers
Answer:
$400
Step-by-step explanation:
450-50=400
Answer:325
Step-by-step explanation: Start off with 150, 150-225=-75 -75-50=-125 -125+450=324 Positive
-
Centimeter using decimal
63mm
Answers
Answer:
6.3cm
Step-by-step explanation:
10mm=1cm
63mm=?cm
(cross multiply)
?=(63mm×1cm)/10mm
?=6.3cm
PLZ HELP
Which polynomial is written in standard form?

Answers
Find the sales tax.
Sales Tax
Selling Price Rate of Sales Tax Sales Tax
$10.00
5%
?
The sales tax is $
Enter your answer in the answer box and then click Check Answer
Answers
Answer:
$0.5
Step-by-step explanation:
10*0.05 = 0.5 dollars
Answer:
.50
Step-by-step explanation:
Selling price x sales tax rate = sales tax
10 x .05 (5%) = .50
What are two possible measures of the angle below? On a coordinate plane, 2 rays form an angle. One ray sits on the x-axis in quadrant 1 and another sits on the y-axis between quadrants 3 and 4. –90° and 630° –45° and 630° –90° and 225° –45° and 225°
Answers
Answer:
–90° and 630°
Step-by-step explanation:
The described angle will be -90° plus any integer multiple of 360°. Possible values for the angle are ...
-90° and 630°
_____
Angles are conventionally measured counterclockwise from the positive x-axis. The angle shown in the attachment is measured clockwise, so represents a negative 90° angle.

Answer:
–90° and 630°
Step-by-step explanation:
The answer above is correct.
when the increase in demand is greater than the decrease in supply, the equilibrium price _____ and the equilibrium quantity _____.
Answers
Answer:
increasedeacreasesWhen the increase in demand is greater than the decrease in supply, the equilibrium price rises and the equilibrium quantity increases.
What is economic equilibrium?
Economic equilibrium, as used in economics, is a state in which forces such as supply and demand are in balance and where, in the absence of external influences, the values of economic variables will remain constant.
The equilibrium quantity rises if the rise in demand outweighs the fall in supply. The equilibrium quantity falls if the rise in demand is smaller than the fall in supply. Equilibrium price rises in each scenario.
The supply and demand curves move in opposition to one another. However, the supply curve shifted to the left while the demand curve shifted to the right (signalling a rise in demand) (indicating a decrease in supply).
In the case increase in demand > decrease in supply
In this instance, the supply curve's leftward movement is proportionally less than the rightward change of the demand curve. So, the price and the equilibrium quantity both increase.
Therefore, the equilibrium price and quantity increases.
To learn more about economic equilibrium from the given link
https://brainly.com/question/13984729
#SPJ4
How do you do this problem?
Find the exact values of sin(2u), cos(2u), and tan(2u) using the double-angles formulas. cot(u)=-3, 3pi/2 < u < 2pi
Answers
By applying the double angle formula and with the information that cot(u) is equal to -3 and u lies between 3pi/2 and 2pi, the values of sin(2u), cos(2u) and tan(2u) can be determined to be -1/sqrt(10), 9/10, and -2/7, respectively.
Using the double angles formula, you can find the exact values of sin(2u), cos(2u), and tan(2u). First, let's look at the double angles formula for sin(2u): sin(2u)=2sin(u)cos(u).
Using the given cot(u)=-3, we can calculate sin(u)=-1/3. Then, cos(u)=sqrt(1-(-1/3)^2)=3/sqrt(10). Therefore, sin(2u)=2sin(u)cos(u)=(-2/3)(3/sqrt(10))= -1/sqrt(10).
Now, let's look at the double angles formula for cos(2u): cos(2u)=cos^2(u)-sin^2(u). Using the calculated values of sin(u) and cos(u) above, we can get cos(2u)=(3/sqrt(10))^2-(-1/3)^2= 9/10.
Finally, let's look at the double angles formula for tan(2u): tan(2u)=2tan(u)/1-tan^2(u). From the given cot(u)=-3, we can calculate tan(u)=-1/3. Therefore, tan(2u)=2tan(u)/1-tan^2(u)=(-2/3)/(1-(-1/3)^2)= -2/7.
Therefore, using the double angles formula, the exact values of sin(2u), cos(2u), and tan(2u) are -1/sqrt(10), 9/10, and -2/7 respectively, given cot(u)=-3 and 3pi/2 < u < 2pi.
To know more about double angles formula refer here:
https://brainly.com/question/30402422?referrer=searchResults
#SPJ11
a(n) ? is a shorthand method for writing a mathematical rule.a. equal sign (=)b. equationc. formulad. math problem
Answers
The equation is a shorthand method for writing a mathematical rule.
The answer to your question is b.equation. An equation is a shorthand method for writing a mathematical rule. It represents a relationship between two or more variables using mathematical symbols and operations. Equations are commonly used in algebra, calculus, and other areas of mathematics to solve problems and make predictions. They are written using an equal sign (=) to show that the expression on the left is equal to the expression on the right. Equations are an important tool in mathematics because they allow us to express complex ideas in a concise and precise way. By using equations, we can simplify calculations and solve problems more efficiently.
Visit here to learn more about the mathematical rule:
brainly.com/question/15502489
#SPJ11
Dita mempunyai pensil sebanyak 10 kotak.Setiap kotak berisi 36 pensil. Pada hari ulang tahunnya, ia membagikan semua pensilnya sama banyak kepada 9 temannya. Berapa banyak pensil yang diterima masing-masing temannya
Answers
Answer:
40 pensil
Step-by-step explanation:
Dari pertanyaan di atas, kita diberitahu bahwa:
Dita memiliki 10 kotak pensil
1 kotak pensil = 36 pensil
10 kotak pensil =
Cross Multiply
10 × 36 = 360 pensil.
Dari pertanyaan tersebut, kami diberitahu bahwa Dita memiliki 9 orang teman dan ia membagikan semua pensilnya secara merata kepada mereka di hari ulang tahunnya.
Jumlah pensil yang diterima setiap teman dihitung sebagai:
360 pensil ÷ 9 teman
= 40 pensil.
Oleh karena itu, setiap teman mendapat 40 buah pensil.
why might a density plot be an important part of the toolkit used by someone building a regression model? density plots will enable an analyst to determine which input variables truly matter in terms of the outcome. a density plot could be a helpful way to view the distribution of a predictor variable. density plots reduce the overall structure of the data. with a density plot, an analyst will be able to see how the prediction model will be built before the model is finalized.
Answers
A density plot is an important tool in the toolkit of someone building a regression model because it can aid in variable selection, model selection, data reduction, and model visualization.
A density plot is a graphical representation of the distribution of a variable.
It can be useful in a regression model because it allows the analyst to visualize the distribution of the predictor variables, which in turn can help determine which variables truly matter in terms of the outcome. This can aid in the selection of input variables for the regression model, ensuring that only the most important variables are included.
Furthermore, a density plot can also provide insight into the shape of the distribution of a predictor variable, which can be helpful in selecting an appropriate regression model.
In addition, a density plot can help reduce the overall structure of the data, making it easier to identify patterns and relationships between variables. This can aid in the creation of a regression model that accurately predicts the outcome based on the input variables.
Finally, by visualizing the distribution of the predictor variables, an analyst can see how the regression model will be built before the model is finalized. This can help ensure that the model is appropriate for the data and that it accurately predicts the outcome.
To know more about regression here.
https://brainly.com/question/14184702
#SPJ4
if m: n=4:5 find the measure of p please help nedd urgent.

Answers
Answer:
let m = 4x
n = 5x
therefore
4x+5x = 180⁰
x = 20⁰
n⁰ = p⁰
5×20⁰ = p⁰
100⁰ = p⁰
Compare h () to the parent function f(0) = cos(0) which statements are true? Select all that apply
Picture included!:)
Answers
While h(x) and f(x) = cos(x) have some differences in their graphs, they share important similarities such as periodicity and amplitude.
Based on the provided picture, h(x) is the function in blue while f(x) = cos(x) is the function in red.
To compare h(x) to the parent function f(x) = cos(x), we need to analyze their similarities and differences.
First, we can observe that both functions are periodic with a period of 2π. This means that the graphs of h(x) and f(x) repeat themselves every 2π units.
Second, both functions have an amplitude of 1. This means that the maximum distance between the graphs and the x-axis is 1 unit.
Third, we can observe that the graph of h(x) is a translation of the graph of f(x) = cos(x). Specifically, the graph of h(x) is shifted 1 unit to the right and 1 unit up compared to the graph of f(x).
Therefore, the following statements are true:
- Both h(x) and f(x) = cos(x) are periodic with a period of 2π.
- Both h(x) and f(x) = cos(x) have an amplitude of 1.
- The graph of h(x) is a translation of the graph of f(x) = cos(x) by 1 unit to the right and 1 unit up.
In summary, while h(x) and f(x) = cos(x) have some differences in their graphs, they share important similarities such as periodicity and amplitude.
To know more about differences visit :-
https://brainly.com/question/28815550
#SPJ11
Translate the sentence into an equation.
Two less than the product of 5 and a number is equal to 4.
Use the variable b for the unknown number.
Answers
Answer:
\(5b - 2 = 4\)
Step-by-step explanation:
two less than implies that we have to subtract 2 from the result of multiplication of 5 and a variable, therefore we get the equation:
\(5b - 2\)
equate it to 4.
Hopefully, this answer helped you
At a point A due South of the building the angle of elevation from the ground to the top of the building is 58゚. At a point B on level ground with a 80 m due West of a the angle of elevation to the top of the building is 27゚. Find the height of the building
Answers
The height of the building from the ground is 83.33 m.
Let h be the height of the building, d be the distance between point A and the building, and d' be the distance between point B and the building.
From the problem, we know that:
The angle of elevation from point A to the top of the building is 58°.The angle of elevation from point B to the top of the building is 27°.Point B is 80 m due West of point A.We can use trigonometry to find the height of the building:
h / d = tan 58°
h = d * tan 58°
Also,
h / d' = tan 27°
h = d' * tan 27°
Since h is the same for both equations, we can set them equal to each other and solve for d:
d * tan 58° = d' * tan 27°
d = d' * tan 27° / tan 58°
We also know that point B is 80 m due West of point A, so we can use the Pythagorean theorem to find the value of d':
d' = √(80² + h²)
Now, we can substitute that into the equation for d and solve for h:
d = d' * tan 27° / tan 58°
h/tan 58° = √(80² + h²) * tan 27° / tan 58°
h=√(80² + h²)*tan 27°
h²cot²27= 80²+h²
1.96h²= 80²+h²
0.96h²=80²
h²= 6944.44
h= 83.33
Read more about Heights and distances:
https://brainly.com/question/9965435
#SPJ4
simplify y=(x+1)(x+2)
Answers
- The distributive property is a basic algebraic property that allows us to distribute a factor to each term inside a set of parentheses. It states that for any real numbers a, b, and c:
\(\sf a(b+c) = ab + ac\) and\(\sf (b+c)a = ba + ca\)- This means that you can multiply a number or variable by a sum or difference by multiplying each term inside the parentheses separately, and then adding or subtracting the resulting products. For example:
\(\qquad\begin{aligned}\sf 3(2 + 5)& =\sf 3(2) + 3(5)\\& =\sf 6 + 15\\&=\sf 21\end{aligned}\)
- This property is useful in simplifying algebraic expressions and solving equations.
Solving the Question:To simplify \(\sf y = (x+1)(x+2)\), we use the distributive property of multiplication:
\(\qquad\begin{aligned}\sf y& =\sf x(x+2) + 1(x+2)\\& =\sf x^2 + 2x + x + 2\end{aligned}\)
Now we combine like terms:
\(\boxed{\bold{\:y = x^2 + 3x + 2\:}}\)Therefore, the simplified form of \(\sf y = (x+1)(x+2)\) is \(\bold{y = x^2 + 3x + 2}\).
To learn more about the distributive property, visit this link below:
https://brainly.com/question/14867533suppose a hypothesis test, using α = 0.05, is being conducted with the following null hypothesis: h0: μ = 2. which one of the following confidence intervals would lead to rejecting the null hypothesis
Answers
A confidence interval cannot instantly lead to rejecting the null hypothesis in a hypothesis test. In the given case the null hypothesis is either rejected or rejected based on test statistics.
α = 0.05
μ = 2
If the confidence interval is 1.0 or 2.0, then the null hypothesis value of 2 drops exceeds the interval, this makes the data contradict the null hypothesis and may reject the null hypothesis.
This alone would not be good to decline the null theory - the conclusion to reject or not reject the null hypothesis is determined by the test statistic and the alternate p-value.
To learn more about Hypothesis
https://brainly.com/question/28920252
#SPJ4
A mathematical sentence indicating that two expressions are not equal.
a.) Linear Equation in one variable
b.) Linear Inequality in one variable
c.) Linear Equation in two variables.
d.) Linear Inequality in two variables
Answers
A mathematical sentence indicating that two expressions are not equal is called a linear inequality.
In mathematics, there are different types of mathematical sentences that represent various relationships between expressions. One such type is a linear equation, which represents an equality between two linear expressions. Another type is a linear inequality, which represents an inequality between two linear expressions. Both linear equations and linear inequalities can be written in one variable or two variables, depending on the number of unknowns involved.
When we have a mathematical sentence indicating that two expressions are not equal, we are dealing with a type of mathematical sentence called a linear inequality. A linear inequality is represented by the symbol '<' (less than), '>' (greater than), '≤' (less than or equal to), '≥' (greater than or equal to), or '≠' (not equal to).
Learn more:
About mathematics here:
https://brainly.com/question/27235369
#SPJ11
The mathematical sentence which is indicating that two expressions are not equal can be stated as : b.) Linear Inequality in one variable.
The correct answer is:
b.) Linear Inequality in one variable.
Here, we have,
we know that,
A linear inequality in two variables can be stated as an inequality that can be written in the form "ax + by < c" or "ax + by > c" or "ax + by = c",
where a is constant, b is constant and c is also constant and x and y both are variables. This inequality which is representing a boundary line and all the solutions of the inequality make up a region of the xy-plane.
As an example we have, the inequality "2x + 3y < 6" represents the region of the xy-plane that is on one side of line 2x + 3y = 6. To graph this inequality, one can find the boundary line by setting the inequality equal to zero and then shading in the region that satisfies the inequality.
A linear equation which is in two variables is an equation that can be written in the form "ax + by = c", where a, b, and c are constants and x and y are variables. This equation that represents a straight line in the xy-plane and all the solutions of the equation are the coordinates of the points on that line.
A mathematical sentence indicating that two expressions are not equal is typically represented by a linear inequality in one variable. In this case, the expressions on both sides of the inequality are not equal to each other.
Hence, The mathematical sentence which is indicating that two expressions are not equal can be stated as : b.) Linear Inequality in one variable.
The correct answer is:
b.) Linear Inequality in one variable.
To learn more on inequality click:
https://brainly.com/question/28841069
#SPJ4
Volume of largest figure
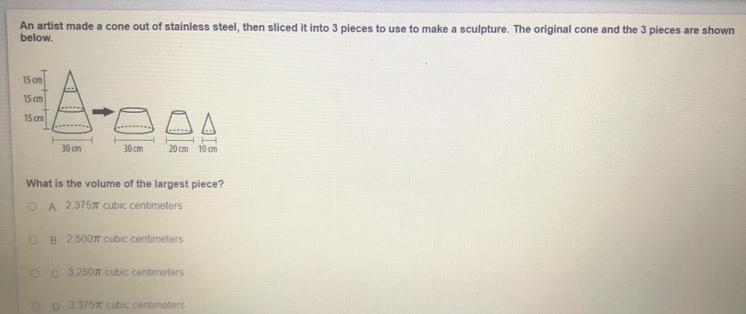
Answers
Answer:
D= 3375
im not gr8 at math lol ;/
min 8x₁ + 6x₂ subject to
a. 4x₁ + 2x₂ ≥ 20
b. −6x₁ + 4x₂ ≤ 12
c. x₁ + x₂ ≥ 6
d. x₁ + x₂ ≥ 0
Answers
The minimum value of the objective function subject to the given constraints is 48 and it occurs at (6,0).
The given problem is:
min 8x₁ + 6x₂ subject to4x₁ + 2x₂ ≥ 20−6x₁ + 4x₂ ≤ 12x₁ + x₂ ≥ 6x₁ + x₂ ≥ 0
The feasible region is as follows:
Firstly, plot the following lines:4x₁ + 2x₂ = 20-6x₁ + 4x₂ = 12x₁ + x₂ = 6x₁ + x₂ = 0On plotting, the following graph is obtained:
Now, let's check each option one by one:
a. 4x₁ + 2x₂ ≥ 20
The feasible region is the region above the line 4x₁ + 2x₂ = 20.
b. −6x₁ + 4x₂ ≤ 12
The feasible region is the region below the line −6x₁ + 4x₂ = 12.c. x₁ + x₂ ≥ 6
The feasible region is the region above the line x₁ + x₂ = 6.d. x₁ + x₂ ≥ 0
The feasible region is the region above the x-axis.
Now, check the point of intersection of the lines.
They are:(10,0),(2,4),(6,0)The point (2,4) is not in the feasible region as it lies outside it.
Therefore, we reject this point.
The other two points, (10,0) and (6,0) are in the feasible region.
Now, check the values of the objective function at these two points.
Objective function value at (10,0): 80
Objective function value at (6,0): 48
Therefore, the minimum value of the objective function subject to the given constraints is 48 and it occurs at (6,0).
Know more about the function here:
https://brainly.com/question/11624077
#SPJ11
If I can read 54 pgs in 3 days, how many can I read in 1 day?
Answers
Answer:
18
Step-by-step explanation:
so all you have to do is divide 54 by 3