A pelican flies to 40 feet above sea level. It then drops down 40 feet to catch a fish. Where is the pelican now? Use the number line below to help you.
Answers
Answer:
Step-by-step explanation:
40 ft - 40 ft = 0
On sea level
Related Questions
DUE IN 52 MINUTES PLEASE HELP IT IS MY LAST QUESTION

Answers
Answer:
(-5.5, -4.5)
Step-by-step explanation:
What is the value of t?

Answers

one card is to be selected at random from a deck of cards. find the probability that the card selected is: a) a 5 b) not a 5 c) a diamond or king d) a jack or queen e) a heart and a club f) a card greater than 6 and less than 9
Answers
The probability of outcome to be a 5 is 1/13. The probability of outcome not be 5 is 12/13. The probability of outcome to be a diamond or a king is 4/13. The probability of the outcomes to be a jack or a queen is 2/13. The probability of The outcome to be a heart and a club is 0 and the probability of the outcomes to be a card greater than 6 and less than 9 is 2/13.
A deck contains a total of 52 cards.
Total outcomes if the selected number of cards is one=52
Case A:
Each suit contain one 5 numbered card. There are four suits. Therefore, The required outcome would be 4.
Probability of an outcome is the ratio of desired outcomes to the total outcomes.
The probability of outcome to be 5, P(A):
P(A)=4/52
P(A)=1/13
Case B:
The total probability of outcomes=52/52=1
The probability of the outcome to be 5=1/13
Therefore, the probability of the outcome not to be 5, P(B):
P(B)=1-(1/13)
P(B)=12/13
Case C:
Each suit carries a king. Therefore, the probability of the outcome to be a king, P(M):
P(M)=4/52
P(M)=1/13
A suit carries 13 cards. Therefore, there will be 13 cards of diamonds.
The probability of the outcome to be a diamond, P(N):
P(N)=13/52
P(N)=1/4
The probability that the outcome is a king of diamonds, P(M\(\cap\)N):
P(M\(\cap\)N)=1/52
Hence, the probability that the outcome is a diamond or a king, P(M\(\cup\)N):
P(M\(\cup\)N)=P(M)+P(N)-P(M\(\cap\)N)
P(M\(\cup\)N)=(1/13)+(1/4)-(1/52)
P(M\(\cup\)N)=16/52
P(M\(\cup\)N)=4/13
Case D:
Each suit carries a Jack. Therefore, the probability of the outcome to be a jack, P(P):
P(P)=4/52
P(P)=1/13
Each suit carries a Queen. Therefore, the probability of the outcome to be a Queen, P(Q):
P(Q)=4/52
P(Q)=1/13
The probability that the outcome is a jack and a queen, P(P\(\cap\)Q):
P(P\(\cap\)Q)=0/52
P(P\(\cap\)Q)=0
Hence, the probability that the outcome is a jack or a queen, P(P\(\cup\)Q):
P(P\(\cup\)Q)=P(P)+P(Q)-P(P\(\cap\)Q)
P(P\(\cup\)Q)=(1/13)+(1/13)-0
P(P\(\cup\)Q)=2/13
Case E:
A card is never a heart and a club. Therefore, the probability of a card to be a heart and a club is 0.
Case F:
The numbers greater than 6 and less than 9 are the numbers between 6 and 9. The numbers between 6 and 9 are 7 and 8.
Each suit carries one 7 numbered card and one 8 numbered card. There is a total of 4 suits.
Therefore the desirable outcomes=8
The probability of the outcome required=8/52
=2/13
Learn more about probability here at:
https://brainly.com/question/28808092
#SPJ4
L is the circle with the equation x²+y²=9
full question in photo :)

Answers
The values of the variables, a, b, and c obtained from the equation of the circle and the coordinates of the point P are;
a) a = 2
b = -2
c = 4
What is the general equation of a circle?The general equation of a circle is; (x - h)² + (y - k)² = r²
Where;
(h, k) = The coordinates of the center of the circle
r = The coordinates of the radius of the circle
The specified equation of a circle is; x² + y² = 9
The coordinates of the center of the circle, is therefore, O = (0, 0)
a) The coordinates of the points P and O indicates that the gradient of OP, obtained using the slope formula is; ((3·√3)/4 - 0)/(3/2 - 0) = ((3·√3)/4)/(3/2)
((3·√3)/4)/(3/2) = (√3)/2
The specified form of the gradient is; (√3)/a, therefore;
(√3)/a = (√3)/2
a = 2
The value of a is 2
b) The gradient of the tangent to a line that has a gradient of m is -1/m
The gradient of OP is; (√3)/2, therefore, the gradient of the tangent at P is -2/(√3)
The form of the gradient of the tangent at P is b/(√3), therefore;
-2/(√3) = b/(√3)
b = -2
The value of b is; -2
c) The coordinate of the point on the tangent, (0, (7·√3)/c) indicates
Slope of the tangent = -2/(√3)
((7·√3)/c - ((3·√3)/4))/(0 - (3/2)) = -2/(√3)
((7·√3)/c - ((3·√3)/4)) = (3/2) × 2/(√3) = √3
(7·√3)/c = √3 + ((3·√3)/4) = 7·√3/4
Therefore; c = 4
Learn more on the equation of a circle here: https://brainly.com/question/12182614
#SPJ1
Mohammed plans to have a fixed amount from his paycheck directly deposited into an account that pays 5.5% interest, compounded monthly. If he gelts pepid on the firm dxy of the month and wants to accumulate $13,000 in the next three-and-a-half years, bow mach me the should he deposit each month?
Answers
Mohammed should deposit approximately $263.16 each month to accumulate $13,000 in the next three-and-a-half years.
To calculate the monthly deposit Mohammed should make, we can use the formula for the future value of an ordinary annuity:
FV = P * [(1 + r)^n - 1] / r,
where:
FV is the future value ($13,000 in this case),
P is the monthly deposit,
r is the monthly interest rate (5.5% divided by 100 and then by 12 to convert it to a decimal),
n is the total number of compounding periods (3.5 years multiplied by 12 months per year).
Plugging in the values, we have:
13,000 = P * [(1 + 0.055/12)^(3.5*12) - 1] / (0.055/12).
Let's calculate it:
13,000 = P * [(1 + 0.004583)^42 - 1] / 0.004583.
Simplifying the equation:
13,000 = P * (1.22625 - 1) / 0.004583,
13,000 = P * 0.22625 / 0.004583,
13,000 = P * 49.3933.
Now, solving for P:
P = 13,000 / 49.3933,
P ≈ $263.16 (rounded to the nearest cent).
Learn more about monthly deposit here: brainly.com/question/29293075
#SPJ11
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
True or false. All rational functions can be gained by transforming y = 1 / x.
Answers
Any graph of a rational function can be obtained from the reciprocal function f(x)=1x f ( x ) = 1 x by a combination of transformations including a translation, stretches and compressions.
8. The straight line depreciation equation for a car is
y = -2,680x + 26,800.
a. How much is the car worth afte-months?
b. How much is the car worth after 75 months?
c. Suppose that M represents the length of time in months when
the car still has value. Write an algebraic expression to represent
the value of this car after M months.
The graph of
O
Answers
An algebraic expression to represent the value of this car after M months is y=Mx+C.
We have given that the
The straight-line depreciation equation for a car is,
y = -2,680x + 26,800.
therefore after 4moths
y = -2,680(4) + 26,800.
y = -10720 + 26,800.
y=16080
What is the slope?
The slope of a line is a measure of its steepness. Mathematically, the slope is calculated as rise over run (change in y divided by change in x)
b. For find after the 75 months replace x by 75 and slolve the given inequality.
Suppose that M represents the length of time in months when
the car still has value.
An algebraic expression to represent the value of this car after M months.
y=Mx+C.
To learn more about the line visit:
https://brainly.com/question/1821791
#SPJ1
(x+y) (x+y) - (x-y) (x-y)
Answers
Answer:
4xy
Step-by-step explanation:
(x+y) (x+y) - (x-y) (x-y)
(x² + xy + xy + y²) - (x² - xy - xy + y²)
(x² + 2xy + y²) - (x² - 2xy + y²)
x² + 2xy + y² - x² + 2xy - y²
x² - x² + 2xy + 2xy + y² - y²
4xy
Answer:
that could literally be anything, as long as the first sum is greater then the second.
example;
(2+4) (3+5) - (6+1) (5+2)
(or, 6+8 = 14, 7+7 = 14, 14 - 14 = 0)
hope this helped :)
I need help and fast!!!!

Answers
Answer:
H. b/a
Step-by-step explanation:
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)
Step 1: Label our variables
y₂ = 2b
y₁ = b
x₂ = 2a
x₁ = a
Step 2: Plug into formula
m = (2b - b)/(2a - a)
Step 3: Evaluate
m = b/a
Answer:
b/a
Step-by-step explanation:
We have two points so we can use the slope formula
m = (y2-y1)/(x2-x1)
= ( 2b - b)/ ( 2a -a)
= b/a
Josh works for 12 hours and makes $84. How many dollars does he make per hour?
Answers
Answer:
7$ dollars per hour
Step-by-step explanation:
Josh makes $7 per hour.
Date:
On
a
farm, there were a total of 440 goats, ducks and chickens.
The number of ducks
was
of the number of chickens. After 1/2 of the goats and of the 1/2 ducks were released, there was a total of 320 goats, ducks and chickens left. Find the number of goats
farm at first.
Answers
Answer:
Step-by-step explanation:
Because we have 3 unknowns, we need to come up with 3 equations. If the total number of animals is 440 and that number is made up of a combination of goats (g), ducks (d), and chickens (c) the first equation is
g + d + c = 440
The next equation is found in the fact that the number of ducks is one-quarter the number of chickens:
\(d=\frac{1}{4}c\) and solving for c gives us that
c = 4d
The last equation says that of the total number of animals, 440, half the goats and half the ducks got away, leaving only 320 animals behind. The last equation, the tricky one, is:
\(440-\frac{1}{2}g-\frac{1}{2}d=320\) and simplifying that:
\(-\frac{1}{2}g-\frac{1}{2}d=-120\) and because nobody hates fractions more than I do, I'm going to get rid of them by multiplying everything by 2 to get:
-g - d = -240
We've got these equations now, but what I'm going to do is to sub in what c equals (c = 4d) for c in the first equation:
g + d + 4d = 440 and
g + 5d = 440 and pair that with the one right above:
-g - 1d = -240 and use elimination to solve. The g's cancel each other out, leaving us with 4d = 200 and d = 50. So there were 50 ducks originally. Now we will sub that in to solve for c:
c = 4d so
c = 4(50) and
c = 200. Now we will sub both those values into the very first equation we put together to solve for g:
g + 200 + 50 = 440 and
g + 250 = 440 so
g = 190.
Add them all together just to be sure we have the 440 that we were told we had in the beginning (and we do, so we're all done!)
Complete the inequality. 13/18___ 11/14 < > =
Answers
Answer:
Your answer is <, Hope it helps.
The number of calls coming in to an office follows a Poisson distribution with mean 5 calls per hour. What is the probability that there will be exactly 7 calls within the next three hours?
a .0.010
b. 0.104
c. 0.090
d.0.071
Answers
The probability of receiving exactly 7 calls in the next three hours is approximately 0.104, which corresponds to answer (b).
To solve this problem, we need to use the Poisson probability formula, which is:
P(X = k) = (e^(-λ) * λ^k) / k!
where X is the number of calls, k is the desired number of calls (7 in this case), λ is the average rate of calls per time period (5 calls per hour), and e is the base of the natural logarithm (approximately 2.71828).
Since we want to know the probability of receiving 7 calls in 3 hours, we need to adjust our λ value accordingly. Since the rate is 5 calls per hour, the average rate for 3 hours would be 5 * 3 = 15 calls.
Now, we can plug these values into the formula:
\(P(X = 7) = (e^(-15) * 15^7) / 7!\)
P(X = 7) ≈ 0.104
So, the probability of receiving exactly 7 calls in the next three hours is approximately 0.104, which corresponds to answer (b).
Learn more about probability here:
https://brainly.com/question/14210034
#SPJ11
In the triangle below a=16. What is the area of the triangle to the nearest hundredth of a unit?

Answers
Answer:
-3.65
Step-by-step explanation:
(16/sin 120) sin 25
help asap --=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-

Answers
Answer:
9 pi
Step-by-step explanation:
First find the circumference of the circle
C =2 * pi *r
C = 2 * pi *9
C = 18 pi
This is a semicircle which is 1/2 of a circle
Take 1/2 of the circumference
1/2 C = 1/2 ( 18 pi)
1/2 C = 9 pi
9 t-shirts and a hat costs £93.00
4 t-shirts and a hat cost £43.00.
How much does a t-shirt cost?
How much does a hat cost?
points and brainlist if you can explain
I need it asap
Answers
1 hat = £10
Answer:
tshirt £10
hat £3
Step-by-step explanation:
there you go the answer
Find the value of the x shown below.

Answers
PLEASE ANSWER THIS IS REALLY IMPORTANT!!!

Answers
Explanation: The y-intercept which is -9 matches with the equation and the slope matches too
I just need number 15 pls it is due in 3 hours
Worth 15 points

Answers
Answer:
Step-by-step explanation:
Don't know. Maybe you add up the two numbers then divide the answer.
Answer:
He is wrong in his approach, because the triangle is a 3,4,5, triangle and he should have put √5^2-4^2
Step-by-step explanation:
Show 76 as tens and ones two ways how do I figure this problem out to get the answer
Answers
Answer: 7 tens and 6 ones
Step-by-step explanation: 76 is two numbers, with a 7 in the tens place and a 6 in the ones place.
76 can be represented as 7 tens and 6 ones or as 6 tens and 16 ones. This involves understanding the place value of digits in a number and knowing that a ten can be broken down into ones.
Explanation:The number 76 can be broken down into tens and ones in multiple ways. First, let's understand what tens and ones mean in the context of a number. In the number 76, '7' is the tens place, and '6' is the ones place, meaning there are 7 tens (70) and 6 ones (6) making up 76.
One way to show 76 with tens and ones is to say that there are 7 tens and 6 ones. This is a very direct method where we just count the number of tens and ones in the number.
Another way we could break down 76 is to say there are 6 tens and 16 ones. This method involves taking one of the tens and breaking it down into 10 ones, giving us a total of 6 tens and 16 ones.
Learn more about Place Value here:https://brainly.com/question/27734142
#SPJ2
Find all solutions of sin x - square 3-3 sin^2x=0
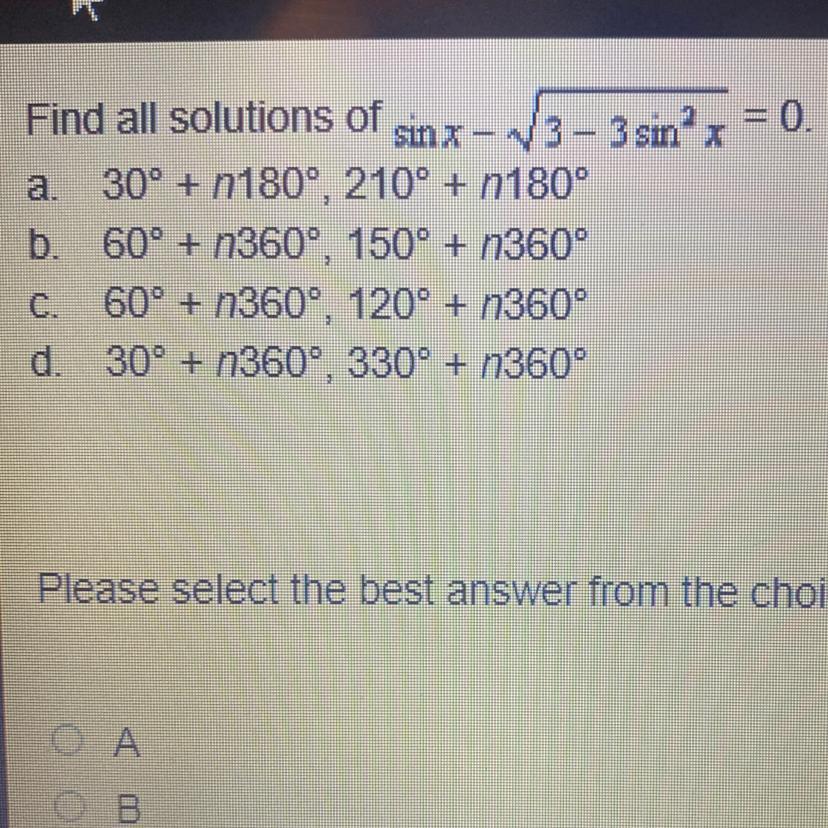
Answers
Answer:
C) \(60^\circ+n360^\circ,120^\circ+n360^\circ\)
Step-by-step explanation:
\(sinx-\sqrt{3-3sin^2x}=0\)
\(sinx=\sqrt{3-3sin^2x} \)
\(sin^2x=3-3sin^2x\)
\(4sin^2x=3\)
\(sin^2x=\frac{3}{4} \)
\(sinx=\pm\sqrt{\frac{3}{4} } \)
\(sinx=\pm\frac{\sqrt{3}}{2} \)
\(x=\frac{\pi}{3}+2\pi n,\frac{2\pi}{3}+2\pi n \)
\(x=60^\circ+n360^\circ,120^\circ+n360^\circ\)
Therefore, the correct option is C
Find the probability of each event
A fair coin is flipped ten times. What is
the probability of the coin landing tails up
at least nine times?
Answers
Answer:
11/1024.
Step-by-step explanation:
Binomial Probability distribution.
This is the probability of 9 tails or 10 tails being flipped.
Prob ( 10 tails) = (1/2)^10 = 1/1024
Prob ( 9 tails) = 10C9 * 1/2^9* 1/2 = 5/512
Required probability = 1/1024 + 5/512
= 11/1024.
a(n) ? is a shorthand method for writing a mathematical rule.a. equal sign (=)b. equationc. formulad. math problem
Answers
The equation is a shorthand method for writing a mathematical rule.
The answer to your question is b.equation. An equation is a shorthand method for writing a mathematical rule. It represents a relationship between two or more variables using mathematical symbols and operations. Equations are commonly used in algebra, calculus, and other areas of mathematics to solve problems and make predictions. They are written using an equal sign (=) to show that the expression on the left is equal to the expression on the right. Equations are an important tool in mathematics because they allow us to express complex ideas in a concise and precise way. By using equations, we can simplify calculations and solve problems more efficiently.
Visit here to learn more about the mathematical rule:
brainly.com/question/15502489
#SPJ11
What’s v=1/3 pi r to the power of 2 h?
Answers
The cone has a height of h = \(\frac{3V}{\pi r^{2} }\)
What is the cone's volume?A geometric object with a three-dimensional shape is called a cone. It features two distinct surfaces, referred to as flat and curved surfaces. A cone is created by connecting the two surfaces. One-third of the area of the base B times the height h equals the volume V of a cone with radius r. The volume of an oblique cone may be calculated using the same formula as a right cone. The volumes of a pyramid and a prism are connected, just as the volumes of a cone and a cylinder are related.
The answer to the question is the provided expression, which represents the cone's volume;
It is spelled as follows:
Volume (V) = \(\frac{1}{3}\pi r^{2}h\)
Now, the formula for calculating height 'h' is displayed below:
h = \(\frac{3V}{\pi r^{2} }\)
As a result, h = \(\frac{3V}{\pi r^{2} }\) is the cone's height.
To learn more about the volume of the cone from the given link:
https://brainly.com/question/1082469
#SPJ9
A dance troupe has a total of 50 dancers split into 2 groups. The costumes worn by Group A cost $80 each, and those worn by Group B cost $90 each. If the total cost of all the costumes is $4,270, what is the total cost of the costumes worn by Group B
Answers
Answer:
2,270
Step-by-step explanation:
HOPE IT HELPED >:D
Answer:
2270 dollars
Step-by-step explanation:
You know each group has 25 dancers and then you multiply 80 by 25 to get the cost of group a. Then you just subtract 2000 from your total to get your answer.
i need this done NOW! ASAP!!!!! pls help help
How do you find the area of a trapezoid?

Answers
Answer:The first one I think
Step-by-step explanation:
Answer:
The formula for the area of a trapezoid is the average of the bases multiplied by the altitude.
Step-by-step explanation:
What does the bar in a fraction mean?
Answers
Answer:
A fraction bar separates the numerator and denominator of a fraction. It indicates that a division of the numerator by the denominator will be performed.
Step-by-step explanation:
In math, a fraction bar can be defined as a visual representation of fractions that helps in comparing fractions and carrying out operations with fractions. Fraction bars or fraction strips are a part-to-whole representational model. Each part of a fraction bar represents one unit out of a whole.
Answer:To separate the top and bottom numbers.
Step-by-step explanation:In math, a fraction bar can be defined as a visual representation of fractions that helps in comparing fractions and carrying out operations with fractions.
Premises:
If I'm a student, then I go to school. If I go to school, then I learn.
Conclusion:
If I'm a student, then I learn.
This is an example of the Law of

Answers
The given statement is an example of the law of detachment.
Given that,
Premises:
If I'm a student, then I go to school. If I go to school, then I learn.
Conclusion:
If I'm a student, then I learn.
This is an example of the Law of which is to be determined.
What is arithmetic?In mathematics, it deals with numbers of operations according to the statements. There are four major arithmetic operators, addition, subtraction, multiplication and division,
Here,
Following the statement given in the premises gives a certain conclusion which shows the detachment behavior.
Thus, the given statement is an example of the law of detachment.
Learn more about arithmetic here:
https://brainly.com/question/11559160
#SPJ5
An airport has two long term parking lots. the cost to park,y, in each lot for x days is shown in the tables
a system of linear equations can be used to determine on which day the cost to park is the same for both lots. one of the equations in the system is y=6x. what is the other equation in the system?

Answers
Answer:
y = 4x + 12 will be the other equation.
Step-by-step explanation:
Data given in the tables show a linear relation (has a common data).
To get the linear relation, we will choose the two points from table (1) .
Let the points are (1, 16) and (2, 20).
Slope of the line 'm' = \(\frac{\triangle{y}}{\triangle{x}}\)
m = \(\frac{20-16}{2-1}\)
m = \(\frac{4}{1}\)
m = 4
Equation of the line passing through (1, 16) having slope = 4
y - 16 = 4(x - 1)
y = 4(x - 1) + 16
y = 4x - 4 + 16
y = 4x + 12
Now we take second set of data,
We choose two points (1, 6) and (2, 12).
Slope 'm' = \(\frac{\triangle{y}}{\triangle{x}}\)
m = \(\frac{12-6}{2-1}\)
m = 6
Equation of the line passing through (1, 6) having slope = 6
y - 6 = 6(x - 1)
y = 6x - 6 + 6
y = 6x
Therefore, other equation of the system of equations will be,
y = 4x + 12