A quotient is a multiple of 5. The dividend is a multiple of 4. The divisor is a factor of 8.
Answers
Yes, as long as the dividend is also a multiple of 5, the equation has sense.
Does the quotient make sense?Here we can define a quotient between two numbers a and b is:
a/b
We know that this is a multiple of 5, so for an integer n we can write:
a/b = 5*n
Now, we know that the dividend is a multiple of 4, so:
a = k*4
The divisor is a factor of 8, the factors of 8 are:
8 = 2*2*2
So the two factors of 8 are 2 and 4.
If the factor is 4, then the problem becomes trivial:
k*4/4 = n*5
k = n*5
So, as long as the dividend is also a multiple of 5, the equation has sense (similar thing happens if the divisor was 2 instead of 4).
Learn more about quotients:
https://brainly.com/question/629998
#SPJ1
Related Questions
the number of fish in a lake decreasing by 400 every year,as described by the function below. f(1)=8200 f(n+1)=f(n)-400 what will be the value
Answers
The number of fish in the lake is an illustration of arithmetic sequence
The value of f(2) is 7800, and it represents the number of fish in the lake, the second year
The model is given as:
\(\mathbf{f(n+1) = f(n) - 400}\)
Where \(\mathbf{f(1) = 8200}\)
To calculate f(2), we simply take n as 1.
i.e. n = 1
Substitute 1 for n in \(\mathbf{f(n+1) = f(n) - 400}\)
So, we have:
\(\mathbf{f(1+1) = f(1) - 400}\)
Add 1 and 1
\(\mathbf{f(2) = f(1) - 400}\)
Substitute 8200 for f(1)
\(\mathbf{f(2) = 8200 - 400}\)
Subtract
\(\mathbf{f(2) = 7800}\)
Hence, the value of f(2) is 7800
Read more about sequence at:
https://brainly.com/question/18109692
*differential equations* *will like if work is shown correctly and
promptly
13. Find a particular solution of the linear system given. x'=3x-y y'=5x-3y where x(0) = 1, y(0) = -1
Answers
the particular solution of the given linear system of differential equations with the given initial conditions x(0) = 1, y(0) = -1 is,
x = (2/3) e^(-5t) + (2/3) e^(3t)
y = (8/5) e^(-5t) - (4/5) e^(3t)
Given the linear system is,
x' = 3x - y ------(1)
y' = 5x - 3y ------(2)
Using initial conditions x(0) = 1, y(0) = -1
Now we solve for x in equation (1),x' = 3x - y
\(dx/dt = 3x - y\)
\(dx/(3x - y) = dt.\)
The left-hand side is the derivative of the logarithm of the absolute value of the denominator, while the right-hand side is the integration of a constant:1/3 ln|3x - y| = t + c1. ------------(3)
Using the initial condition x(0) = 1,
x(0) = 1 = (1/3) ln|3(1) - (-1)| + c1c1
= 1/3 ln(4) + k1c1
= ln(4^(1/3)k1)
Now, substituting the value of c1 in equation (3),
1/3 ln|3x - y| = t + 1/3 ln(4) + k1
Taking exponentials,
|3x - y| = e^3 (4) e^3 (k1) e^3t
3x - y = ± 4e^3 e^3t e^3(k1) ----- (4)
Now, we solve for y in equation (2),y' = 5x - 3ydy/dt = 5x - 3ydy/(5x - 3y) = dt
The left-hand side is the derivative of the logarithm of the absolute value of the denominator, while the right-hand side is the integration of a constant:1/5 ln|5x - 3y| = t + c2. -------------(5)Using the initial condition y(0) = -1,
y(0) = -1
= (1/5) ln|
5(1) - 3(-1)| + c2
c2 = -1/5 ln(8) + k2
c2 = ln(8^(-1/5)k2)
Now, substituting the value of c2 in equation (5),
1/5 ln|5x - 3y| = t - 1/5 ln(8) + k2
Taking exponentials,
|5x - 3y| = e^(-5) (8) e^(-5k2) e^5t
5x - 3y = ± 8e^(-5) e^(-5t) e^(-5k2) -------------- (6)
Equations (4) and (6) are a system of linear equations in x and y.
Multiplying equation (4) by 3 and equation (6) by -1,
we get: 9x - 3y = ± 12e^3 e^3t e^3(k1) ----- (7)
3y - 5x = ± 8e^(-5) e^(-5t) e^(-5k2) ------------ (8)
Adding equations (7) and (8),
12x = ± 12e^3 e^3t e^3(k1) ± 8e^(-5) e^(-5t) e^(-5k2)
Hence, x = ± e^3t (e^(3k1)/2) ± 2/3 e^(-5t) (e^(-5k2))
Multiplying equation (4) by 5 and equation (6) by 3, we get:
15x - 5y = ± 20e^3 e^3t e^3(k1) ----- (9)
9y - 15x = ± 24e^(-5) e^(-5t) e^(-5k2) ------------ (10)
Adding equations (9) and (10),
-10y = ± 20e^3 e^3t e^3(k1) ± 24e^(-5) e^(-5t) e^(-5k2)
Therefore, y = ± 2e^3t (e^(3k1)/2) ± 12/5 e^(-5t) (e^(-5k2))
Thus, the general solution of the given linear system of differential equations is,
x = ± e^3t (e^(3k1)/2) ± 2/3 e^(-5t) (e^(-5k2))
y = ± 2e^3t (e^(3k1)/2) ± 12/5 e^(-5t) (e^(-5k2))
Now, using the given initial conditions x(0) = 1, y(0) = -1,
we have,1 = ± (e^(3k1)/2) + 2/3 (-1)
= ± (e^(3k1)/2) + 12/5
Solving the above two equations simultaneously, we get,
k1 = ln(4/3),
k2 = -ln(5/3)
Hence, the particular solution of the given linear system of differential equations with the given initial conditions x(0) = 1,
y(0) = -1 is,
x = (2/3) e^(-5t) + (2/3) e^(3t)
y = (8/5) e^(-5t) - (4/5) e^(3t)
To learn more about Linear visit;
https://brainly.com/question/31510530
#SPJ11
Given, y<−x+a and y>x+b
In the xy-plane, if (0,0) is a solution to the system of inequalities above, which of the following relationship between a and b must be true?
A.a>b
B.b>a
C.∣a∣>∣b∣
D.a=−b
Answers
The correct relationship between a and b that must be true in the given system of inequalities is ∣a∣ > ∣b∣. The answer is C
What is a system of inequalities?
A system of inequalities refers to a set of multiple inequalities that are considered simultaneously. The solution to the system consists of all the values that satisfy each inequality in the system. It represents a region in the coordinate plane where the shaded area encompasses all the valid solutions for the given set of inequalities.
Given the inequalities y < -x + a and y > x + b, we know that the point (0,0) satisfies both of these inequalities. Plugging in x = 0 and y = 0 into the inequalities, we get:
0 < a (from y < -x + a)
0 > b (from y > x + b)
From these equations, we can conclude that a must be greater than 0 (since 0 < a) and b must be less than 0 (since 0 > b). To compare their magnitudes, we take the absolute values:
∣a∣ > 0 (since a > 0)
∣b∣ < 0 (since b < 0)
Since the magnitude of a (∣a∣) is greater than the magnitude of b (∣b∣), the correct relationship is ∣a∣ > ∣b∣, which is option C.
To know more about inequalities, refer here:
https://brainly.com/question/2293190
#SPJ4
find the solution to mx cx kx=f(t) for an arbitrary function f(t), x(0)=0, x'(0)=0
Answers
Step-by-step explanation:
The given equation `mx cx kx=f(t)` is a second-order linear differential equation with constant coefficients. The general solution to this type of equation is given by the sum of the complementary solution `x_c(t)` and the particular solution `x_p(t)`.
The complementary solution x_c(t) is the solution to the associated homogeneous equation mx cx kx=0. The characteristic equation for this homogeneous equation is mr^2 + cr + k = 0. Solving this quadratic equation gives two roots r_1 and r_2. The complementary solution can then be written as x_c(t) = C_1e^(r_1t) + C_2e^(r_2t).
The particular solution x_p(t) depends on the form of the function f(t). There are several methods for finding the particular solution, such as undetermined coefficients or variation of parameters.
Once the complementary and particular solutions are found, the general solution to the given differential equation is given by x(t) = x_c(t) + x_p(t). The constants C_1 and C_2 can then be determined using the initial conditions x(0)=0 and x'(0)=0.
Without more information about the function f(t), it is not possible to find a more specific solution to the given differential equation.
a. When x = -1, what is the value of y?
b. When y = 7, what is the value of x?
c. What is the y-intercept of the graph?
d. What is the x-intercept of the graph?
e. What is the slope of the line?
f. What is the equation of the line?

Answers
Answer:
a. When x = -1, the value of y = 3
b. When y = 7, the value of x = 1
c. The y-intercept is (0, 5)
d. The x-intercept is (-2.5, 0)
e. The slope of the line is 2
f. The equation of the line is y = 2x + 5
Step-by-step explanation:
The form of the linear equation is y = m x + b, where
m is the slopeb is the y-intercept (value y at x = 0)The x-intercept is the value of x at y = 0
From the given graph:
a.
∵ x = -1
→ Look at the graph and find the y-coordinate of the point on
the line whoes x-coordinate = -1
∴ y = 3
∴ When x = -1, the value of y = 3
b.
∵ y = 7
→ Look at the graph and find the x-coordinate of the point on
the line whose y-coordinate = 7
∴ x = 1
∴ When y = 7, the value of x = 1
c.
∵ The y-intercept of the graph is the point of intersection of
the graph and the y-axis
→ Look at the graph and find the y-coordinate of the point on
the line whose x-coordinate = 0
∴ y = 5
∴ The y-intercept is (0, 5)
d.
∵ The x-intercept of the graph is the point of intersection of
the graph and the x-axis
→ Look at the graph and find the x-coordinate of the point on
the line whose y-coordinate = 0
∴ x = -2.5
∴ The x-intercept is (-2.5, 0)
e.
∵ The slope of the line m = Δy/Δx
→ Use the intercepts to find it
∵ The intercepts are (-2.5, 0) and (0, 5)
∴ Δx = 0 - (-2.5) = 2.5
∴ Δy = 5 - 0 = 5
∴ m = 5/2.5 = 2
∴ The slope of the line is 2
f.
∵ The form of the equation of the line is y = m x + b
∵ m = 2
∵ b = 5
∴ y = 2x + 5
∴ The equation of the line is y = 2x + 5
The equation of the line is y = 2.27x + 5.
We are given that;
The graph of the line
Now,
a. When x = -1
y= 3
b. When y = 7
x= 1
c. The y-intercept of the graph= 7
d. The x-intercept of the graph= 3.5
The slope of the line can be calculated using the formula:
slope = (y2 - y1) / (x2 - x1)
where (x1, y1) = (0,5) and (x2, y2) = (-2.2,0).
Substituting the values in the formula we get:
slope = (0 - 5) / (-2.2 - 0) = 5 / 2.2 ≈ 2.27
The equation of the line can be found using the slope-intercept form of a line which is given by:
y = mx + b
where m is the slope and b is the y-intercept.
We already know that m ≈ 2.27.
To find b we can use either of the two points. Let (0,5):
y = mx + b 5 = 2.27(0) + b b = 5
Therefore, by the equation answer will be y = 2.27x + 5.
To learn more about equation:
brainly.com/question/16763389
#SPJ1
In a class of students, the following data table summarizes how many students play
an instrument or a sport. What is the probability that a student chosen randomly
from the class plays a sport?
Plays a sport
Does not play a sport
Plays an instrument Does not play an instrument
3
8
10
9
Answers
Answer:
3 OR 8 hope this helps!
Step-by-step explanation:
Use the figure to find the specified angle measure. In the figure, II q
Suppose m <4=82. Find m<5

Answers
Solve for x. (hint: same-side interior angles)

Answers
Answer:
32
Step-by-step explanation:
3x + 20 + 2x = 180 (angles lying on the same side of the transversal are supplementary)
=> 5x + 20 = 180
=> 5x = 180 - 20
=> 5x = 160
=> x =160/5 (by transposing)
=> x = 32
Hope you understood!!
The value of x in the given figure is 32 .
Here,
Both 2x and 3x + 20 degrees are on same side of transversal (l) .
So the both are supplementary angles.
So,
3x + 20 + 2x = 180 (angles lying on the same side of the transversal are supplementary)
So,
=> 5x + 20 = 180
=> 5x = 180 - 20
=> 5x = 160
=> x =160/5 (by transposing)
=> x = 32
Know more about supplementary angles,
https://brainly.com/question/18289138
#SPJ4
What is another expression to show 9/2
Answers
Answer:
9 ÷ 2
Step-by-step explanation:
or draw that small house thing over the 9 an place 2 to the left of it.
c) Using Gary's age come up with an expression that represents your age in terms of g. Be creative! For example, if Mr. Weiler is 43 years old, then his age would be 4g-1.
Answers
We know that Gary's age is 11 years old. So, we just have to use an expression to indicate someone's age.
Let's consider the expression:
\(2g+5\)This expression represents Mr. Smith's age who is 27 years old. Let's prove it using Gary's age.
\(2(11)+5=22+5=27\)Therefore, our expression is 2g + 5.Identify whether the figure has plane symmetry, symmetry about an axis, or neither. HELP NEEDED NOW!!!




Answers
Answer:
The plane figure has a symmetry about an axis
Answer:
plane symmetry and symmetry about an axis
Step-by-step explanation:
A three-dimensional figure has plane symmetry if a plane can divide the figure into two congruent reflected halves.So, the given figure has seven plane symmetries.
A three-dimensional figure has symmetry about an axis if there is a line about which the figure can be rotated by an angle greater than 0∘ and less than 360∘ so that the image coincides with the preimage.So, the given figure has symmetry about seven axes.
Therefore, the figure has plane symmetry and symmetry about an axis.
8. For each of the following polynomials, determine whether it is irreducible over the given ring and prove your answers.
(a) f(x) = 33 + x2 - 86 - 8; Z (b) g() = 4x + 2? +3; Z (c) h(x) = 162 - 2x2 +5; Q (d) px) = 2x + 1822 -- 15x+6; Q (e) g(x) = 1044 - x + x +7Q 9. Prove that Za[1/(x2 + + +1) is a field. How many elements does this field have?
Answers
(a) The polynomial f(x) = 3x^2 - 8x - 86 over Z is irreducible.
(b) The polynomial g(x) = 4x + 2 over Z is irreducible.
(c) The polynomial h(x) = 16x^2 - 2x + 5 over Q is irreducible.
(d) The polynomial p(x) = 2x^3 + 18x^2 - 15x + 6 over Q is irreducible.
(e) The polynomial g(x) = 10x^4 - x^3 + x^2 + 7 over Q is irreducible.
Za[1/(x^2 + x + 1)] is a field and has an infinite number of elements.
(a) The polynomial f(x) = 3x^2 - 8x - 86 over Z has no integer roots, making it irreducible over Z.
(b) The polynomial g(x) = 4x + 2 over Z is a linear polynomial and is irreducible over Z.
(c) The polynomial h(x) = 16x^2 - 2x + 5 over Q has no rational roots, so it is irreducible over Q.
(d) The polynomial p(x) = 2x^3 + 18x^2 - 15x + 6 over Q has no rational roots, indicating its irreducibility over Q.
(e) The polynomial g(x) = 10x^4 - x^3 + x^2 + 7 over Q does not have any rational roots, making it irreducible over Q.
Za[1/(x^2 + x + 1)] is a field, satisfying the field axioms. It has an infinite number of elements since it consists of all rational functions with coefficients in Z, where the denominator is the polynomial x^2 + x + 1.
Learn more about irreducible polynomials: brainly.com/question/31472385
#SPJ11
What numbers are located exactly 5/3 units from point P on the number line?

Answers
The required numbers are -2.33 and 1 are a distance of 5/3 unit from -2/3 on a number line.
What is Number Line?In math, a number line can be defined as a straight line with numbers arranged at equal segments or intervals throughout. A number line is typically shown horizontally and can be extended indefinitely in any direction.
Here, we have,
We have been given that number line, the numbers that are 5/3 units away from the number -2/3 are the numbers that are 5/3 units to its right and left.
The numbers are given by -2/3 - 5/3 and -2/3 + 5/3.
So the required numbers would be:
⇒ -2/3 - 5/3 = -7/3 = -2.33
⇒ -2/3 + 5/3 = 3/3 = 1
Therefore, the required numbers are -2.33 and 1 are a distance of 5/3 unit from -2/3 on a number line.
Learn more about the number line here:
brainly.com/question/17617832
#SPJ2
Evaluate the complex number (5 angle 10 degree)(10 angle -40 degree)/13 angle -80 degree)(6 angle -130 degree). The value of the given complex number is .
Answers
The value of the given complex number is 0.641 ∠ 180°.
By multiplying the numerator and denominator, we may make the complex number expression (5 ∠ 10°)(10 ∠ -40°)/(13 ∠ -80°)(6 ∠ -130°) easier to evaluate.
We multiply the magnitudes and add the angles when multiplying complex numbers in polar form.
The numerator can be summed up as follows:
(5 ∠ 10°)(10 ∠ -40°) = (5 * 10) ∠ (10° - 40°) = 50 ∠ -30°
The denominator simplifies as follows:
(13 ∠ -80°)(6 ∠ -130°) = (13 * 6) ∠ (-80° - 130°) = 78 ∠ -210°
Now, we divide the numerator by the denominator:
(50 ∠ -30°)/(78 ∠ -210°) = (50/78) ∠ (-30° - (-210°)) = (25/39) ∠ 180°
The value of the given complex number is (25/39) ∠ 180°, which can also be written as approximately 0.641 ∠ 180°.
To learn more about complex number link is here
brainly.com/question/20566728
#SPJ4
The complete question is:
Evaluate the complex number (5∠10°)(10∠-40°)/13∠-80°)(6∠-130°). The value of the given complex number is ________.
PLEASE HELP THIS IS MY LAST QUESTION
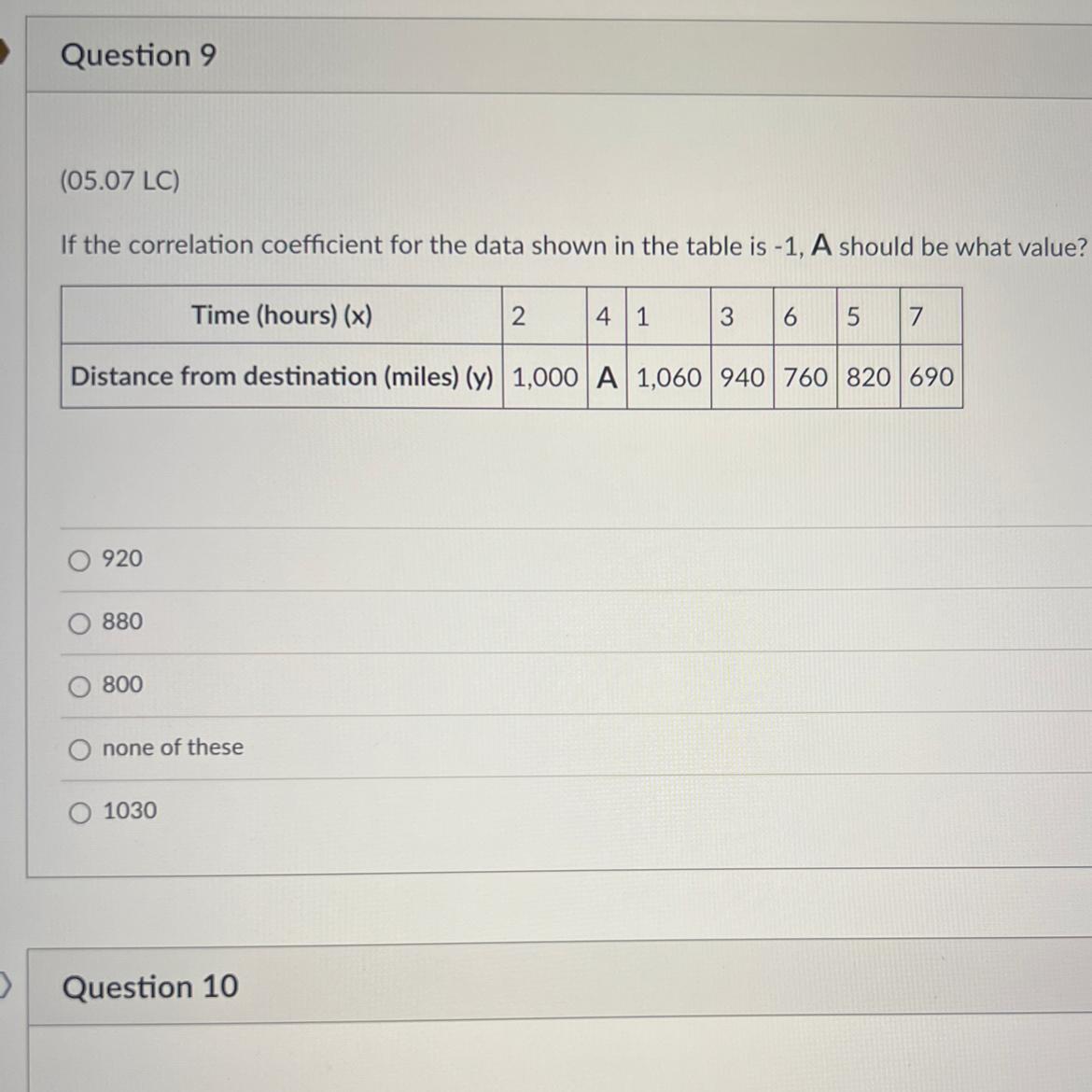
If the correlation coefficient for the data shown in the table is -1, A should be what value?
Time (hours) (x)
4 1
3 6 5 7
Distance from destination (miles) (y) 1,000 A 1,060 940 760 820 690
920
880
800
none of these
O 1030
2
Answers
Answer:
Step-by-step explanation:
Here is the answer
The correlation coefficient measures the strength of the linear relationship between two variables, and it ranges from -1 to 1. A correlation coefficient of -1 indicates a perfect negative linear relationship between the variables, which means that as one variable increases, the other decreases at a constant rate.
To find the value of A in this scenario, we need to look for a perfect negative linear relationship between the two variables, time (x) and distance from destination (y). The table shows that as time increases, the distance from the destination decreases, but we need to find the exact rate of change.
We can calculate the rate of change by finding the slope of the line that represents the relationship between time and distance. We can use the formula for the slope of a line, which is:
slope = (change in y) / (change in x)
If we choose the first and last points in the table, we get:
slope = (690 - 1060) / (7 - 1) = -70
This means that for every hour of time that passes, the distance from the destination decreases by 70 miles. Therefore, if the correlation coefficient is -1, we should see a perfect negative linear relationship between time and distance, with a slope of -70.
To check if A is the correct value, we can use the formula for the equation of a line in slope-intercept form:
y = mx + b
where m is the slope and b is the y-intercept. We can plug in the values of m and b and solve for A:
y = -70x + b
If we use the first point in the table, where x = 4 and y = 1000, we get:
1000 = -70(4) + b
b = 1220
So the equation of the line is:
y = -70x + 1220
If we plug in the values of x for the remaining points in the table, we get:
y = 1030 when x = 0
y = 880 when x = 2
y = 800 when x = 3
y = A when x = 5
y = 760 when x = 6
To find the value of A, we can plug in the corresponding value of y and solve for A:
1030 = -70(0) + 1220
880 = -70(2) + 1220
800 = -70(3) + 1220
760 = -70(6) + 1220
A = -70(5) + 1220 = 850
Therefore, the value of A should be 850 if the correlation coefficient for the data shown in the table is -1.
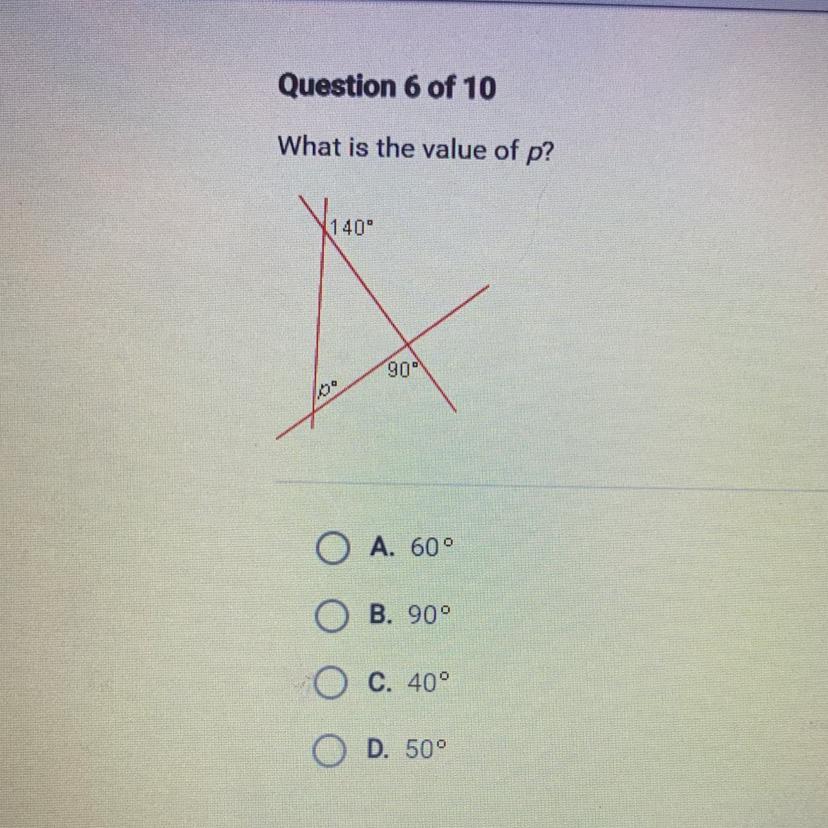
Question 6 of 10
What is the value of p?
140"
90
lo
O A. 600
ОО
B. 900
C. 40°
O D. 50°
Answers
Answer:
B answer is correct hiiii
Answer: 50
Step-by-step explanation:
Determine the normal and shear stress on plane a, determine the principal stresses at the point, determine the maximum shear stress at the point, draw the principal element
Answers
The principal stresses are those that act on the principal planes. There are three principal stresses on a point under force.
What is principal stress?The principal stresses are those that act on the principal planes. The plane bearing the greatest normal stress is referred to as the principal plane, and the stress acting on it is referred to as the principal stress.
When a force is applied on an inclined plane, the force can be divided into two subparts, the first component of the force is perpendicular to the plane and is known as the normal force, while the second component of the force is parallel to the plane and is known as the shear stress.
The principal stresses at a point can be found using the following formulas, therefore, the principal stresses will be,
\({\sigma}'_{xx}=\sigma_{xx}cos(2\theta)+\sigma_{yy}sin(2\theta)+2\tau_{xy}sin(\theta)cos(\theta)\)
\({\sigma}'_{yy}=\sigma_{xx}sin(2\theta)+\sigma_{yy}cos(2\theta)-2\tau_{xy}sin(\theta)cos(\theta)\)
\({\tau}'_{xy}=(\sigma_{yy}-\sigma_{xx})sin\theta cos\theta+\tau_{xy}(cos2\theta-sin2\theta)\)
Hence, there are three principal stresses on a point under force.
Learn more about Principal Stress:
https://brainly.com/question/14418799
#SPJ4
Derek saves 10% of his paycheck each week to buy a mountain bike the mountain bike costs 340.00 Derek receives a paycheck in the amount of $280.50 each week how many paychecks will Derek have to receive before he has saved enough money to buy the mountain bike
Answers
Answer: 13 weeks
Step-by-step explanation:
First you have to find 10% of 340.00 which is 28, so each week he saves 28.00 for his bike. To find how many paychecks he has to recieve you divide 340.00 by 28.00, which is 12.1, since there is a decimal place you have to round it up to 13 because it is a little bit more than 12 paychecks. ;)
click on screenshot and please answer

Answers
Answer:
Step-by-step explanation:
To find the length of the pole, use Pythagorean theorem,
4.6m = 4.6*100 = 460 cm
hypotenuse² = base² + altitude²
altitude² = hypotenuse² - base²
=460² - 280²
= 211600 - 78400
= 133200
altitude = √133200 = 364.97 cm
Length of the pole = 364.97 cm
b) Length of stair² = 95² + 364*94²
= 9025 + 133200
= 142225
Length of stair= √14225 = 377.13
Length of stair = 377.13 cm
Which graphs represents a function?

Answers
Answer: The one below the top.
Step-by-step explanation: In order to tell if it is a function or not, you need to do the vertical line test. By examining the graph you can see that majority of the graphs has two points in the same x-axis. The only one that pasts the test is the graph below the top one.
Answer: The second one is because there can't be two y's in a straight line of a function and all of the other graphs have two y's in a line.
Step-by-step explanation:
one factor of 8x^3+1 is 2x+1 The other factor is?
Answers
So that you have 2^3*x^3+1
Multiply the terms with equal exponents by multiply the bases (1 is basically the same as 1^3)
So that it becomes (2x)^3+1^3
Then, using a^3+b^3 equals (a+b)(a^2-2ab+b^2), factor the expression so that it becomes
(2x+1)((2x)^2-2x+1^2)
Expand the second bracket
So the two factors are (2x+1) and (4x^2-2x+1)
What function/equation is best for this

Answers
Please help finding the value of x
Please
Answers
To "solve for x" is to identify the x value that indicates that the equation is true. We should obtain L.H.S = R.H.S once we figure out the value of x and replace it in the equation .x + 2 = 7
Add 2 to both sides, resulting in x = 5 when x + 2 - 2 = 7 - 2
Re-entering the solution, x = 5, will allow you to verify the answer.
We get 5 + 2= 7.
Because LHS = RHS
Apply mathematical operation to the both the equation's two halves to bring the variable with one side as well as the additional values to the other side in order to find the value of x.
If I were to ask you to find a number for x that satisfied the equation
"x + 1 = 2," you would have to do the same.
To know more about equation click here
brainly.com/question/28243079
#SPJ4
"Complete question"
Find the value of x and use it to solve the problem. x + 2 = 7
find a vector equation and parametric equations for the line segment that joins p to q. p(3.5, −4.4, 3.1), q(1.8, 0.3, 3.1) vector equation r(t) = parametric equations (x(t), y(t), z(t)) =
Answers
The vector equation for the line segment that joins point P(3.5, -4.4, 3.1) to point Q(1.8, 0.3, 3.1) can be written as:x(t) = 3.5 - 1.7t,y(t) = -4.4 + 4.7t,z(t) = 3.1
r(t) = P + t(Q - P)
where P represents the position vector of point P, Q represents the position vector of point Q, and t is a scalar parameter.
Substituting the given values into the equation, we have:
r(t) = (3.5, -4.4, 3.1) + t[(1.8, 0.3, 3.1) - (3.5, -4.4, 3.1)]
Simplifying the equation, we get:
r(t) = (3.5, -4.4, 3.1) + t(-1.7, 4.7, 0)
This is the vector equation for the line segment joining points P and Q.
To obtain the parametric equations for the line segment, we can express the x, y, and z coordinates of the equation separately as functions of the parameter t.
These are the parametric equations that represent the x, y, and z coordinates of the line segment joining points P and Q.
The vector equation for a line segment represents a linear combination of two position vectors, which in this case are the position vectors of points P and Q. The parameter t represents a scalar that scales the direction and magnitude of the line segment.
By subtracting the position vector of point P from the position vector of point Q, we obtain the direction vector of the line segment. Multiplying this direction vector by the scalar parameter t and adding it to the position vector of point P gives us the position vector of any point on the line segment.
To obtain the parametric equations, we express each coordinate (x, y, z) separately as a function of the parameter t. By isolating the x, y, and z components, we can see how each coordinate varies as the parameter t changes.
In this case, the x-coordinate decreases by 1.7 units for every unit increase in t, while the y-coordinate increases by 4.7 units for every unit increase in t. The z-coordinate remains constant at 3.1.
By plugging different values of t into the parametric equations, we can obtain the corresponding coordinates of points on the line segment. These equations allow us to trace the trajectory of the line segment and determine the position of any point along it.
know more about vector equation :brainly.com/question/31044363
#SPJ11
The average age of undergraduate students at grand canyon university is 44. if the standard deviation is 4, what percentage of undergraduate students are between 36 and 52 years old?
Answers
75% is percentage of undergraduate students are between 36 and 52 years old.
What is percentage and example?
A percentage is a ratio or fraction where the full value is always 100. For example, if Sam received 30% marks in his math test, it signifies that he scored 30 marks out of 100. In ratio form, it is expressed as 30:100 and in fraction form as 30/100.The percentage is used to determine “how much” or “how many.” A percentage number aids in calculating the exact amount or figure that is being discussed. Fractions are compared.This would be true if k=3, but k=2
because (36-44)/4 = -2 and (52-44)/4 = 2
Learn more about percentage
brainly.com/question/28269290
#SPJ4
I'm not good at functions

Answers
1,16
2,14
4,10
5,8
Answer:
When x is equal to 1, y is equal to 18-2(1), which is equal to 16.
When x is equal to 2, y is equal to 18-2(2), which is equal to 14.
When x is equal to 4, y is equal to 18-2(4), which is equal to 10.
When x is equal to 5, y is equal to 18-2(5), which is equal to 8.
Let me know if this helps!
1. Kylie mowed Mr. Johnson's lawn for
4 weeks. Every week Mr. Johnson
paid Kylie $15.43. How much money
did Kylie earn after the four weeks?
$71.62
c. $60.72
b. $61.72
d. $70.62
Answers
Answer:
The answer is b. $61.72
Step-by-step explanation:
Since she mowed the lawn for 4 weeks, and each week Kylie earned $15.43, then 4 x 15.43 = $61.72 after 4 weeks.
B. $61.72
Shelley is making strawberry popsicles to have by the pool on a hot summer day. She
combines the ingredients in a blender shaped like a square prism with a 4-inch by 4-inch
square base. When she is done blending, the strawberry popsicle mixture fills the blender to
a height of 5.8 inches. The popsicle molds she will fill are cylindrical with a radius of 0.6
inches and a height of 4.5 inches.
What is the maximum number of popsicle molds Shelley can fill completely with the popsicle
mixture?
in
Answers
Answer:
18
Step-by-step explanation:
Explanation is in photo

20 points pleaseeeeeeeeee help!!

Answers
the answer is d I'm pretty for sure
Add. -3 5/6 + 1 5/6 =
Answers
Answer:
-2
Step-by-step explanation:
hope it helps