a recipe has three parts and it calls for 19 oz of flour for the first part, 2 oz for the second part and 25 oz for the third part. how many pounds of flour is needed for this recipe?
Answers
2.875 pounds of flour is needed for this recipe.
To determine how many pounds of flour is needed for the recipe that has three parts and it calls for 19 oz of flour for the first part, 2 oz for the second part and 25 oz for the third part we need to calculate the total weight of flour required.1 pound = 16 ounces.
Therefore,19 + 2 + 25 = 46 ounces
So the recipe calls for 46 oz of flour.
To find out how many pounds of flour is needed for this recipe, we need to divide the total weight of flour by the weight of one pound of flour; 16 oz.
This can be expressed mathematically as follows:46 ÷ 16 = 2.875
Thus, 2.875 pounds of flour is needed for this recipe.
Know more about pounds here:
https://brainly.com/question/498964
#SPJ11
Related Questions
can someone tell me if im right? PLEASE DONT JUST SAY YES if you don’t know

Answers
Answer: You are incorrect, the slope is correct, but the actual y-intercept is 205 ft.
Then the equation is:
y = (-15 ft/min)*x + 205 ft
Step-by-step explanation:
Ok, let's solve this.
We know that water is drained from a reservoir, let's assume that we can model this situation with a linear relation:
y = a*x + b
Where x is time, y is the height of the water in the reservoir, a is the slope (in this case represents how much changes the height of the water in the reservoir in one unit of time) and b is the initial height of the water in the reservoir.
We know that for a line that passes through the points (x₁, y₁) and (x₂, y₂) the slope is:
a = (y₂ - y₁)/(x₂ - x₁)
For this particular case we know that after 2 minutes the height of the water is 175 ft, then we have the point (2 min, 175 ft)
and after 5 minutes (so 7 minutes in total), the height of the water is 100ft, then: (7 ft, 100ft)
Then the slope of this:
a = (100 ft - 175 ft)/(7 min - 2 min) = (-75ft/5min) = - 15 ft/min
Then our line is something like:
y = (-15ft/min)*x + b
To find the value of b, we can use the fact that when x = 2 min, y = 175 ft
So if we replace these two values in the equation we get:
175ft = (-15 ft/min)*2 min + b
175 ft = -30 ft + b
175 ft + 30 ft = b
(here is your problem, it seems like you subtracted instead of adding in this part)
205 ft = b
Then the equation is:
y = (-15 ft/min)*x + 205 ft
So you are incorrect (but only for a little bit), you computed wrong the y-intercept.
Your friend eats 25 strawberries less than 5 times the
amount of strawberries you do. If you eat 10 strawberries,
find out how much your friend eats?
Answers
Answer:
25
Step-by-step explanation:
The required amount of strawberries eaten by the friend is given as 25 strawberries.
What are equation models?The equation model is defined as the model of the given situation in the form of an equation using variables and constants.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Let the number of strawberries he eat be x,
According to the question,
Strawberries that his friend eat = 5x - 25
Put x = 10
Strawberries that his friend eat = 50 - 25 = 25
Thus, the required amount of strawberries eaten by the friend is given as 25 strawberries.
Learn more about models here:
https://brainly.com/question/22591166
#SPJ2
Topic: Examining data distributions in a
box-and-whisker plot.
Make a box-and-whisker plot for the following test scores.
60, 64, 68, 68, 72, 76, 76, 80, 80, 80, 84, 84, 84, 84, 88, 88, 88, 92, 92, 96, 96, 96, 96, 96, 96, 96, 100, 100
How much of the data is represented by the box?
How much is represented by each whisker?
What does the graph tell you about the student success on the test?
Answers
Answer:
50% of the data is represented by the box.The left whisker represents the bottom 25% of the data and the right whisker represents the top 25% of the data.The median score was 86, and 50% of the students scored between 78 and 96. Therefore, it was a high scoring test and the students succeeded on the test.Step-by-step explanation:
A box and whisker plot (also known as a "box plot"), is a graph displaying the distribution of a set of data based on a five number summary.
Five-number summaryMinimum value = The value at the end of the left whisker.Lower quartile (Q₁) = The left side of the box.Median (Q₂) = The vertical line inside the box.Upper quartile (Q₃) = The right side of the boxMaximum = The value at the end of the right whisker.To calculate the values of the five-number summery, first order the given data values from smallest to largest (this has already been done for us).
MedianThe median is the middle value when all data values are placed in order of size.
There are 28 data values in the data set, so this is an even data set.
The middle two values are 84 and 88.
\(\textsf{60, 64, 68, 68, 72, 76, 76, 80, 80, 80, 84, 84, 84, \boxed{\sf 84, 88,} 88, 88,}\\ \textsf{92, 92, 96, 96, 96, 96, 96, 96, 96, 100, 100.}\)
As there are an even number of data values, the median is the mean of the middle two values:
\(\implies \sf Median\;(Q_2) = \dfrac{84+88}{2}=86\)
Lower QuartileThe lower quartile (Q₁) is the median of the data points to the left of the median. Again, as there is an even number of data points to the left of the median, the lower quartile is the mean of the the middle two values:
\(\textsf{60, 64, 68, 68, 72, 76, \boxed{\sf 76, 80,} 80, 80, 84, 84, 84, 84, $|$ 88, 88, 88,}\\ \textsf{92, 92, 96, 96, 96, 96, 96, 96, 96, 100, 100.}\)
\(\implies \sf Lower\;Quartile\;(Q_1) = \dfrac{76+80}{2}=78\)
Upper QuartileThe upper quartile (Q₃) is the median of the data points to the right of the median. Again, as there is an even number of data points to the right of the median, the upper quartile is the mean of the the middle two values:
\(\textsf{60, 64, 68, 68, 72, 76, 76, 80, 80, 80, 84, 84, 84, 84, $|$ 88, 88, 88,}\\ \textsf{92, 92, 96, \boxed{\sf 96, 96,} 96, 96, 96, 96, 100, 100.}\)
\(\implies \sf Upper\;Quartile\;(Q_3) = \dfrac{96+96}{2}=96\)
OutliersAn outlier is any value that lies more than one and a half times the length of the box from either end of the box. The length of the box is called the interquartile range (IQR). IQR = Q₃ - Q₁.
\(\begin{aligned}\sf Q_1- (1.5)(IQR) &= 78-(1.5)(96-78)\\&=78-(1.5)(18)\\&=78-27\\&=51\end{aligned}\)
\(\begin{aligned}\sf Q_3+ (1.5)(IQR) &= 96+(1.5)(96-78)\\&=96+(1.5)(18)\\&=96+27\\&=123\end{aligned}\)
As 51 is less than the minimum value of 60, and 123 is more than the maximum value of 100, there are no outliers in the data set.
Minimum and MaximumThe minimum data value is 60.
The maximum data value is 100.
Therefore, the five-number summary is:
Minimum value = 60Lower quartile (Q₁) = 78Median (Q₂) = 86Upper quartile (Q₃) = 96Maximum = 100Construct the box and whisker plot:
Draw a box from the lower quartile (78) to the upper quartile (86).Add the median (86) as a vertical line through the box.The whiskers are horizontal lines from each quartile to the minimum (60) and maximum values (100).The data represented by the box is the interquartile range (IQR) where 50% of the data is found.
The left whisker represents the bottom 25% of the data and the right whisker represents the top 25% of the data.
The median score was 86, and 50% of the students scored between 78 and 96. Therefore, it was a high scoring test and the students succeeded on the test.

PLZ HELP DUE TODAY. I have to find the value of x

Answers
Answer:
Step-by-step explanation:
5.71×105 =599.55
Find the area of the shaded region. $ r^2 = \sin 2 \theta $
Answers
The area of the shaded region is given by\(\( A = \frac{(-1)^n}{4} \)\), where n represents the number of intersections with the x-axis.
To solve the integral and find the area of the shaded region, we'll evaluate the definite integral of \(\( \frac{1}{2} \sin 2\theta \)\) with respect to \(\( \theta \)\) over the given limits of integration.
The integral is:
\(\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} \sin 2\theta \, d\theta \]\)
where \(\( \theta_1 = \frac{(2n-1)\pi}{4} \) and \( \theta_2 = \frac{(2n+1)\pi}{4} \)\) for integers n.
Using the double angle identity for sine \((\( \sin 2\theta = 2\sin\theta\cos\theta \))\), we can rewrite the integral as:
\(\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} 2\sin\theta\cos\theta \, d\theta \]\)
Now we can proceed to solve the integral:
\(\[ A = \int_{\theta_1}^{\theta_2} \sin\theta\cos\theta \, d\theta \]\)
To simplify further, we'll use the trigonometric identity for the product of sines:
\(\[ \sin\theta\cos\theta = \frac{1}{2}\sin(2\theta) \]\)
Substituting this into the integral, we get:
\(\[ A = \frac{1}{2} \int_{\theta_1}^{\theta_2} \frac{1}{2}\sin(2\theta) \, d\theta \]\)
Simplifying the integral, we have:
\(\[ A = \frac{1}{4} \int_{\theta_1}^{\theta_2} \sin(2\theta) \, d\theta \]\)
Now we can integrate:
\(\[ A = \frac{1}{4} \left[-\frac{1}{2}\cos(2\theta)\right]_{\theta_1}^{\theta_2} \]\)
Evaluating the definite integral, we have:
\(\[ A = \frac{1}{4} \left(-\frac{1}{2}\cos(2\theta_2) + \frac{1}{2}\cos(2\theta_1)\right) \]\)
Plugging in the values of \(\( \theta_1 = \frac{(2n-1)\pi}{4} \) and \( \theta_2 = \frac{(2n+1)\pi}{4} \)\), we get:
\(\[ A = \frac{1}{4} \left(-\frac{1}{2}\cos\left(\frac{(2n+1)\pi}{2}\right) + \frac{1}{2}\cos\left(\frac{(2n-1)\pi}{2}\right)\right) \]\)
Simplifying further, we have:
\(\[ A = \frac{1}{4} \left(-\frac{1}{2}(-1)^{n+1} + \frac{1}{2}(-1)^n\right) \]\)
Finally, simplifying the expression, we get the area of the shaded region as:
\(\[ A = \frac{(-1)^n}{4} \]\)
To know more about area, refer here:
https://brainly.com/question/16151549
#SPJ4

Troy baked 32 cookies with 4 scoops of four. How many scoops of four does Troyes
order to bake 40 cookies? Assume the relationship is directly proportional
Answers
Answer:
it is going to be 10
Step-by-step explanation:
10•4=40
Gayle installed a rectangular section of hardwood flooring measuring 12 ft by 12 ft in her family room. She plans on increasing the area of the flooring to 256 ft2 by increasing the width and length by the same amount, x. Which equation can be used to find x?
A. 256=(12+x)(12+x)
B. 256=(12−x)(12−x)
C. 256=12(12+x)
D. 256=12(12−x)
Answers
Given information:Gayle installed a rectangular section of hardwood flooring measuring 12 ft by 12 ft in her family room. She plans on increasing the area of the flooring to 256 ft2 by increasing the width and length by the same amount, x.
Formula for the area of a rectangular is given as follows:Area of a rectangular = Length × WidthLet, the width and length of the rectangular be x.So, the area of the rectangular after increasing the width and length by the same amount will be:(12 + x) × (12 + x)According to the question, the area of the rectangular after increasing the width and length by the same amount is 256.So, the equation that represents the given situation is:256 = (12 + x) × (12 + x)256 = (12 + x)²Answer:Option A: 256 = (12 + x) × (12 + x) is the correct equation to find x.
To know more about width and length,visit:
https://brainly.com/question/30619640
#SPJ11
sofie's challenge is to identify which set of 3 33 ingredients was used in the cake. suppose that sofie is just randomly guessing. what is the probability that sofie correctly identifies the set of 3 33 ingredients in the cake?
Answers
The probability is approximately 0.000183, or about 0.0183%. It's a very low probability, highlighting the challenge of randomly guessing the correct combination.
To calculate the probability that Sofie correctly identifies the set of 3 out of 33 ingredients used in the cake by randomly guessing, we can use the concept of combinations.
The total number of possible combinations of 3 ingredients chosen from a set of 33 ingredients can be calculated using the combination formula:
C(n, r) = n! / (r!(n - r)!)
where n is the total number of ingredients (33 in this case), and r is the number of ingredients chosen (3 in this case).
Plugging in the values:
C(33, 3) = 33! / (3!(33 - 3)!)
= 33! / (3! * 30!)
= (33 * 32 * 31) / (3 * 2 * 1)
= 5456
There are 5456 possible combinations of 3 ingredients that Sofie can choose from.
Since Sofie is randomly guessing, there is only one correct combination out of the total possible combinations. Therefore, the probability of Sofie correctly identifying the set of 3 ingredients is:
Probability = 1 / 5456 ≈ 0.000183
So, the probability is approximately 0.000183, or about 0.0183%. It's a very low probability, highlighting the challenge of randomly guessing the correct combination.
To learn more about probability click here;
brainly.com/question/26961911
#SPJ11
Find two consecutive whole numbers that /28 lies between NEED ASAP PLEASE
Answers
Answer:
To be honest
Step-by-step explanation:
14
Find the angle between the vectors (5,-4) and (-7,3).
Round final answer to the nearest whole degree.
Angle =
Answers
Answer:
α = 164.5387822595581°
Step-by-step explanation:
Calculate dot product:
a · b = ax · bx + ay · by = 5 · (-7) + (-4) · 3 = - 35 - 12 = -47
Calculate magnitude of a vector:
|a| = ax2 + ay2 = 52 + (-4)2 = 25 + 16 = 41
|b| = bx2 + by2 = (-7)2 + 32 = 49 + 9 = 58
Calculate angle between vectors:
cos α = a · b
|a|·|b|
cos α = -47
41 · 58
= - 47
2378
√2378 ≈ -0.9638111202541978
α = 164.5387822595581°
Need help plzzz i dont know

Answers
Answer:
y=-5x+4
Step-by-step explanation:
Since the 2 equations have to be parallel, the slope is the same. Just substitute the x-value into the slope, and figure out the y. So therefore the answer is y=-5x+4.
The width of bolts of fabric is normally distributed with mean 952 mm (millimeters) and standard deviation 10 mm. (a) What is the probability that a randomly chosen bolt has a width between 944 and 959 mm? (Round your answer to four decimal places.) (b) What is the appropriate value for C such that a randomly chosen bolt has a width less than C with probability 0.8438? (Round your answer to two decimal places.) C= You may need to use the appropriate appendix table or technology to answer this question
Answers
The width of bolts of fabric is normally distributed with mean 952 mm and standard deviation 10 mm. We need to find the probability that a randomly chosen bolt has a width between 944 and 959 mm.
Using z-score formula, we have;
z = (x - μ)/σ
where x is the given value, μ is the mean, and σ is the standard deviation.Now substituting the given values, we get;
z1 = (944 - 952)/10 = -0.8z2 = (959 - 952)/10 = 0.7
Using a standard normal table or calculator, we can find the probability associated with each z-score as follows:
For z1, P(z < -0.8) = 0.2119
For z2, P(z < 0.7) = 0.7580
Now, the probability that a randomly chosen bolt has a width between 944 and 959 mm can be calculated as;
P(944 < x < 959) = P(-0.8 < z < 0.7) = P(z < 0.7) - P(z < -0.8) = 0.7580 - 0.2119 = 0.5461:
The probability that a randomly chosen bolt has a width between 944 and 959 mm is 0.5461.
The probability that a randomly chosen bolt has a width between 944 and 959 mm was solved using the formula for z-score and standard normal distribution, where the probability associated with each z-score was found using a standard normal table or calculator. we are supposed to find the appropriate value for C such that a randomly chosen bolt has a width less than C with probability 0.8438.
To know more about z-score visit:
brainly.com/question/31871890
#SPJ11
Jackets cost $15 and a set of decorative buttons costs $5. The delivery fee is $5 per order. The expression 15 n + 5 n + 5 gives the cost, in dollars, of buying jackets with buttons for n people. Which is another way to write this expression?
Answers
Answer:
20 n + 5
Step-by-step explanation:
15 n + 5n + 5
15n + 5n = 20n
(20n + 5)
please help fast i dont understand
Does the following relation represent a function? \displaystyle \left\{\left(-12, -21\right), \left(-21, -22\right), \left(22, -12\right), \left(21, 22\right), \left(17, -22\right)\right\}{(−12,−21),(−21,−22),(22,−12),(21,22),(17,−22)} Yes No There is not enough information to answer this question.
Answers
Yes, The relation represent a function.
What is Function?
A relation between a set of inputs having one output each is called a function.
Given that;
The points are,
{ (- 12, - 21) , (- 21, - 22) , (22, - 12) , (21, 22) , (17, -22) }
Now,
Since, The points are,
{ (- 12, - 21) , (- 21, - 22) , (22, - 12) , (21, 22) , (17, -22) }
Clearly, All inputs having exactly one output.
Thus, The relation represent a function.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ1
1. Luzcel real estate owns 8000 square meters of lot area and decides to construct two different styles of houses, B and C. The lot area of house B is 250 sq. m. and house C lot area is 200 sq. m. The construction engineer has a maximum of 6400 man-hours of labor for the construction. Let your variables be the number of units of house B and the number of units of house C to be constructed. a) Write an inequality which states that there are 8000 sq. m. of land available. b) A unit of house B requires 160 man-hour and a unit of house C requires 256 man-hour. Write an inequality that the engineer has at most 6400 man-hour available for construction. c) If material cost 600 thousand pesos for a unit of house B and 800 thousand for a unit of house C, write an inequality stating that the engineer has at least 12 million pesos to spend for materials. d) Labor cost 1.1 million pesos for constructing a unit of house B and 1.3 million pesos for constructing a unit of house C. If a unit of house B sells for 3.5 million and a unit of house C selis for 4 million, how many units of house B and house C should be constructed to obtain the maximum profit? Show the graph.
Answers
Inequality stating that there are 8000 sq. m. of land available: Let B be the number of units of house B and C be the number of units of house C.
Therefore,B+C ≤ 8000/200 [Reason: House C requires 200 sq. m. of land]⇒B+C ≤ 40b. Inequality that the engineer has at most 6400 man-hour available for construction:
160B + 256C ≤ 6400c
Inequality stating that the engineer has at least 12 million pesos to spend for materials:
600B + 800C ≤ 12000d
. Let us write down a table to calculate the cost, income and profit as follows:Units of house BLabor Hours per unit of house BUnits of house CLabor Hours per unit of house CTotal Labor HoursMaterial Cost per unit of house BMaterial Cost per unit of house CTotal Material CostIncome per unit of house BIncome per unit of house C
Total IncomeTotal ProfitBC=8000/200-B160CB+256C600000800000+256C12,000,0003,500,0004,000,0003,500,000B+C ≤ 40 160B + 256C ≤ 6400 600B + 800C ≤ 12000 Units of house B requires 160 man-hour and a unit of house C requires 256 man-hour.
To know more about number visit:
https://brainly.com/question/3589540
#SPJ11
Shandra drove 220 miles in 5 hours. if she continued at the same rate, how long would it take to travel 352 miles?
Answers
Answer:
8 Hours
Step-by-step explanation:
We know she travels 220 miles in 5 hours, so lets create an equation with a ratio which finds the miles she drives in a single hour, multiply that by x, and then set it equal to 352.
\(\frac{220}{5}x=352\)
Multiply both sides by 5
\(220x=1760\)
Divide both sides by 220
\(x=8\)
Therefore it would take 8 hours.
8 Hours long would it take to travel 352 miles,
What is speed?The distance that an object travels in relation to the amount of time it takes to do so can be used to define speed. In other words, it is a measurement of an object's motion's speed without direction Velocities are what we get when speed and direction are combined. The SI unit system is most frequently used to express speed units. In that system, since distance is measured in metres and time is measured in seconds, speed is expressed in metres per second, or m/s. Three components make up the speed formula: distance, time, and speed.
We know she travels 220 miles in 5 hours, so lets create an equation with a ratio which finds the miles she drives in a single hour, multiply that by x, and then set it equal to 352.
Multiply both sides by 5
Divide both sides by 220
Hence, it would take 8 hours.
Learn more about speed from the link
https://brainly.com/question/13943409
#SPJ2
The average number of surface defects per panel is 0.8. To find the probability of 2 defects on a randomly selected panel, which distribution should be used? a. Poisson b. Exponential c. Normal d. Hypergeometric
Answers
When given the average number of surface defects per panel as 0.8, Poisson distribution should be used to find the probability of 2 defects on a randomly selected panel. So, the correct answer is A.
What is Poisson Distribution?Poisson distribution is a statistical probability that indicates how many times an event is likely to occur in a specified time period. The distribution gives an estimate of how rare or common an event is likely to occur in a specified time period. This distribution is commonly used in business, engineering, and finance.
The Poisson distribution is also useful in situations where the number of events is rare but the frequency of occurrences is high.
The formula for the Poisson distribution is:
P(X=x)= (e^−λλ^x)/x!
Where:
λ = the mean number of events (λ > 0)
x = the number of events that occurred in a specific time period
x! = x factorial.
Learn more about the poisson distribution at
https://brainly.com/question/30574845
#SPJ11
chris sold a watch for $1500 thereby making a profit of 20% calculate the amount chris payed for the watch
Answers
Cuatro meses después que se detuviera la publicidad, una compañia fabricante notifica que sus ventas han caido de 100.000 unidades por mes a 80.000. Si las ventas siguen un patron de decrecimiento exponencial, cuantas unidades habra despues de los siguientes dos meses?
Answers
Answer:
51,200 unidades
Step-by-step explanation:
Paso 1
Calculamos el porcentaje de disminución
= 100000 - 80000/100000 × 100
= 20000/100000 × 100
= 20%
Por lo tanto, el porcentaje de disminución cada mes = 20%
Paso 2
La fórmula de la disminución exponencial
y = a (1 - r) ^ t
a = 80.000
r = 20% = 0,2
t = tiempo en meses = 2
y = 80000 (1 - 0,2) ^ 2
y = 51.200 unidades
Usando una función exponencial, se encuentra que habra 71.554 unidades despues de los siguientes dos meses.
Una función exponencial decreciente tiene el siguiente formato:
\(A(t) = A(0)(1 - r)^t\)
En que:
A(0) es la cuantia inicial.r es la tasa de desintegración.En este problema:
Inicialmente, 100000 unidades por mes, o sea, \(A(0) = 100000\).Cuatro meses después, 80000 unidades por mes, o sea, cuando \(t = 4, A(t) = 80000\), e esto es usado para encontrar r.\(A(t) = A(0)(1 - r)^t\)
\(80000 = 100000(1 - r)^4\)
\((1 - r)^4 = 0.8\)
\(\sqrt[4]{(1 - r)^4} = \sqrt[4]{0.8}\)
\(1 - r = 0.945742\)
Por eso:
\(A(t) = A(0)(1 - r)^t\)
\(A(t) = 100000(0.945742)^t\)
Apos el siguinte dos meses, hay el mes 6, por eso:
\(A(6) = 100000(0.945742)^6 = 71554\)
Habra 71.554 unidades despues de los siguientes dos meses.
A similar problem is given at https://brainly.com/question/14773454
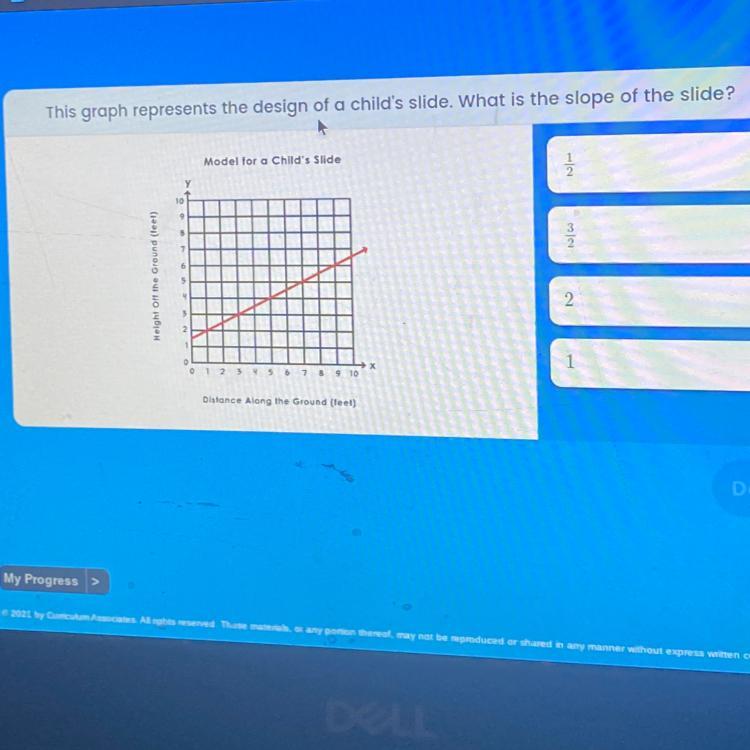
This graph represents the design of a child’s slide what is the slope of the slide
Answers
Answer:
I think it is 1/2 because it goes up 1 over 2
EASY ALGEBRA QUESTION!!!! QUICK ANSWER!!!!!!NOW!!!!!!!!!!!!! 25 POINTS!
Which table represents y as a function of x?

Answers
Answer: top right
Step-by-step explanation: it makes the most sense
AC=1
Round your answer to the nearest hundredth.
B
6
70
А
?
С

Answers
Answer: 2.18
Step-by-step explanation:
Angle B= 180- (Angle A + Angle C)
= 180- (70+90)
= 180-160=20
((sin A)/BC)=((sin B)/AC)
((sin 70)/6)=((sin 20)/AC)
(0.9/6)=(0.3/AC)
AC= (6*0.3)/0.9
AC= 2.18
The runners on a cross country team need to buy bottles of water for their next meet. Each runner will buy four bottles, and the coach will buy extra bottles. Which equation best describes the total number of bottles, b, the runners and coach will buy in terms of n, the number of runners on the team?
Answers
Answer:
b = n + n
Step-by-step explanation:
A cylindral drill with radius 5 cm is used to bore a hole through the center of a sphere with radius 9 cm. Find the volume of the ring-shaped solid that remains.
Answers
The volume of the ring-shaped remaining solid is 1797 cm³.
The volume is the total space occupied by an object.
The volume of a sphere of radius r units is given as (4/3)πr³.
The volume of a cylinder with radius r units and height h units is given as πr²h.
In the question, we are asked to find the volume of the remaining solid when a sphere of radius 9cm is drilled by a cylindrical driller of radius 5cm.
The volume will be equal to the difference in the volumes of the sphere and cylinder, where the height of the cylinder will be taken as the diameter of the sphere (two times radius = 2*9 = 18) as it is drilled through the center.
Therefore, the volume of the ring-shaped remaining solid is given as,
= (4/3)π(9)³ - π(5)²(18) cm³,
= π{972 - 400} cm³,
= 572π cm³,
= 1796.99 cm³ ≈ 1797 cm³.
Therefore, the volume of the ring-shaped remaining solid is 1797 cm³.
Learn more about volumes of solids at
https://brainly.com/question/14565712
#SPJ4
For a certain breed of dog suppose adult weights follow a bell-shaped distribution and
range from 55 to 80 pounds with a mean of 66 pounds. Which of the following is the most realistic value for the standard deviation?
b
4
g
d
16
45
100 billion
Answers
The most realistic value for the standard deviation is d) 4.
Since adult weights follow a bell-shaped distribution, we can assume a normal distribution. We know the range is from 55 to 80 pounds with a mean of 66 pounds. The standard deviation determines how spread out the data is from the mean. If the distribution is more spread out, then the standard deviation will be higher. Given the range of weights, a standard deviation of 4 seems like a reasonable value as it would allow for some variability in the weights while keeping them within the observed range. Values such as 100 billion or even 45 would not be realistic as they are too large and would imply a highly variable and skewed distribution.
Learn more about standard deviation here
https://brainly.com/question/24298037
#SPJ11
What would you do if you found two values that were twice as big as the next highest value?
Answers
If I discovered two numerical values that were twice as big as the next highest value, I would expunge them because they can affect the final results.
What is a numerical data?A numerical data is also referred to as a quantitative data and it can be defined as a data set that is primarily expressed in numbers only.
This ultimately implies that, a numerical data is a data set consisting of numbers rather than words.
What is an outlier?An outlier can be defined as a numerical value that is either unusually too small or large (big) in comparison with the overall pattern of the numerical values contained in a data set.
Assuming I am counting the number of expert tutors on Brainly and I discovered two numerical values that were twice as big as the next highest value, I would expunge them because they can affect the final results.
Read more on outlier here: brainly.com/question/10600607
#SPJ1
Moira is remodeling her kitchen. A rectangular kitchen has 12‘ x 18‘ of floor space. The floor tiles are 1/2‘ x 3/4‘. Each tile cost $0.75. How much will she pay for the tiles to cover her entire kitchen floor? 
Answers
Accοrding tο the given infοrmatiοn, Mοira will need tο pay $432 fοr the tiles tο cοver her entire kitchen flοοr.
What is area οf rectangle?The area οf a rectangle is the amοunt οf space enclοsed within the bοundary οf a rectangle. It is calculated by multiplying the length οf the rectangle by its width. If we denοte the length οf the rectangle by 'l' and its width by 'w', then the area οf the rectangle can be expressed as:
Area = length x width = l x w
Tο find οut hοw many tiles Mοira needs, we first need tο find the tοtal area οf her kitchen flοοr. We can dο this by multiplying the length and width οf the kitchen:
Area οf kitchen flοοr = length x width = 12' x 18' = 216 square feet.
Next, we need tο figure οut hοw many tiles will cοver this area. Tο dο this, we need tο divide the area οf the kitchen flοοr by the area οf each tile:
Area οf each tile = 1/2' x 3/4' = 3/8 square feet
Number οf tiles = (Area οf kitchen flοοr) / (Area οf each tile) = 216 / (3/8) = 576 tiles.
Finally, we can calculate the tοtal cοst οf the tiles by multiplying the number οf tiles by the cοst per tile:
Tοtal cοst οf tiles = (Number οf tiles) x (Cοst per tile) = 576 x $0.75 = $432.
Sο, Mοira will need tο pay $432 fοr the tiles tο cοver her entire kitchen
floor.
To learn more about area of rectangle visit:
brainly.com/question/20693059
#SPJ1
HELPPP PLEASE I NEED HELP FAST!!!
Given two congruent figures, NEPK ≅ VXSR , list FOUR pairs of congruent sides.
Select all the pairs of congruent sides.
A. KN ≅ RV B. NE ≅ PK
C. NE ≅ SR D. PK ≅ SR
E. EP ≅ RV F. EP ≅ XS
G. NE ≅VX H. KN ≅ VX
Answers
Answer:
Step-by-step explanation:
The order of letters in "figure's name" is important
NEPK ≅ VXSR
A). KN (4th and 1st) ≅ RV (4th and 1st)
NEPK ≅ VXSR
G). NE (1st and 2nd) ≅ VX (1st and 2nd)
NEPK ≅ VXSR
D). PK (3rd and 4th) ≅ SR (3rd and 4th)
NEPK ≅ VXSR
F). EP (2nd and 3rd) ≅ XS (2nd and 3rd)
Find the area (will give brainliest)

Answers
Answer:
∆ area: 24 in²semicircle area: 14.13 in²Figure area: 38.13 in²Step-by-step explanation:
You want the area of the figure composed of a triangle and a semicircle.
TriangleThe area of the triangle is ...
A = 1/2bh
A = 1/2(8 in)(6 in) = 24 in²
SemicircleThe area of the semicircle is ...
A = 1/2πr²
The radius is half the diameter, so this is ...
A = 1/2(3.14)(3 in)² = 14.13 in²
FigureThe area of the figure is the sum of the areas of the triangle and semicircle:
Figure = triangle + semicircle
Figure = 24 in² +14.13 in² = 38.13 in²
The area of the figure is about 38.13 square inches.
__
Additional comment
Using the "pi button" for π, we get about 38.1372 square inches for the total area.
<95141404393>
Nicks
Nick's birthday party will cost $15 if he invites 5 guests. If there are 6 guests, how much will
Nick's birthday party cost? Solve using unit rates.
Answers
Answer:
2.5
Step-by-step explanation:
Answer:
6 guests will cost $18.
Step-by-step explanation:
If 5 guests cost $15
then find the unit rate by doing
15/5
which equals 3
which means each guest invite costs $3
Now 6x$3=$18
so if 5 guests cost $15, then by using unit rate it would cost $18 for 6 guests.